湖南省怀化市通道县2022-2023学年八年级下学期期末考试数学试卷(含答案)
文档属性
| 名称 | 湖南省怀化市通道县2022-2023学年八年级下学期期末考试数学试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 488.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-04 08:44:01 | ||
图片预览



文档简介
2023年八年级期末卷
数 学
温馨提示:
(1)本学科试卷分试题卷和答题卷两部分,考试时量为120分钟,满分为150分.
(2)请你将姓名、准考证号等相关信息按要求填涂在答题卡上.
(3)请你按答题卡要求,在答题卡上作答,答在本试题卷上无效.
一、选择题(每小题4分,共40分)
1、直角三角形的一锐角是40°,那么另一锐角是( )
A. 40° B. 50° C. 60° D.70°
2、一个多边形的内角和为1440°,那么这个多边形是( )
A.十边形 B.九边形 C.八边形 D.七边形
3、点P(-2,3)关于x轴对称的点是( )
A.(2,3) B. (-2,-3) C.(2,-3) D. (3,-2)
4、 下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
5、下列函数是关于自变量的一次函数的是( )
A. B. C. D.
6、抛掷两枚质量和形状相同的硬币,则出现“一正一反”的频率是( )
A.1 B. C. D.
如图,在△ABC中,∠C=90°,AC=BC,AD是角平分线,CD=,那么AB的长是( )
A. B.
C. D.
8、正比例函数的函数值随的增大而减小,则一次函数的图象大致是( ).
9、下列命题中,真命题是( )
A. 对角线互相平分的四边形是平行四边形
B. 有一组邻边相等且对角线互相垂直的四边形是菱形
C. 有一个角是直角且对角线相等的四边形是矩形
D. 对角线互相垂直平分的四边形是正方形
10、一个四边形的边长依次是,b,c,d且满足,则这个四边形是( )
A. 矩形 B. 菱形 C.正方形 D. 平行四边形
二、填空题(每小题4分,共24分)
11、函数中自变量的取值范围是 ;
如图,为了测量古塔的高,小明在点A测得看古塔顶点C
处的仰角为30°,然后向古塔方向前进到40米的点B处测
得古塔顶点C的仰角是60°,A、B、D在同一直线上,那
么古塔CD的高是 米.(,结果保留一位小数)
如图,在菱形ABCD中,边AB=5,对角线AC=6,那么,
这个菱形ABCD的面积是 ;
14、已知一次函数的图形经过第一、三、四象限,那么,的取值范围是___________.
15、如图,两个边长为4的正方形部分重叠在一起,点O是一个
正方形的中心,另一个正方形的顶点与点O重合,并绕着O
点旋转,那么重叠部分的面积是 ;
16、如图,在平面直角坐标系中,已知点A(4,0)和
点B(2,3),A、B、O、D四点是平行四边形的顶点,
那么点D的坐标是 .
二、解答题(共86分)
17、(8分)如图,在平面直角坐标系中,△ABC的顶点都在网格点上. 写出A、B、C三点的坐标;
画出△ABC关于y轴的对称图形△A1B1C1;
画出把△ABC向右平移五个单位长度,然后再
向上平移四个单位长度的图形△A2B2C2.
18.(8分)如图,AD是△ABC的高,AD=BD,BE=AC,∠BAC=80°.求∠DBE的度数.
19、(10分)如图,平面直角坐标系中,直线经过点A(-2,1)和点B(1,4).
求直线的表达式;
求△OAB的面积.
20.(10分)如图,在□ABCD中,∠ABC=70°,BE平分∠ABC,交AD于E,AB=3cm,ED=1cm.
求∠A,∠C,∠D的度数;
求□ABCD的周长.
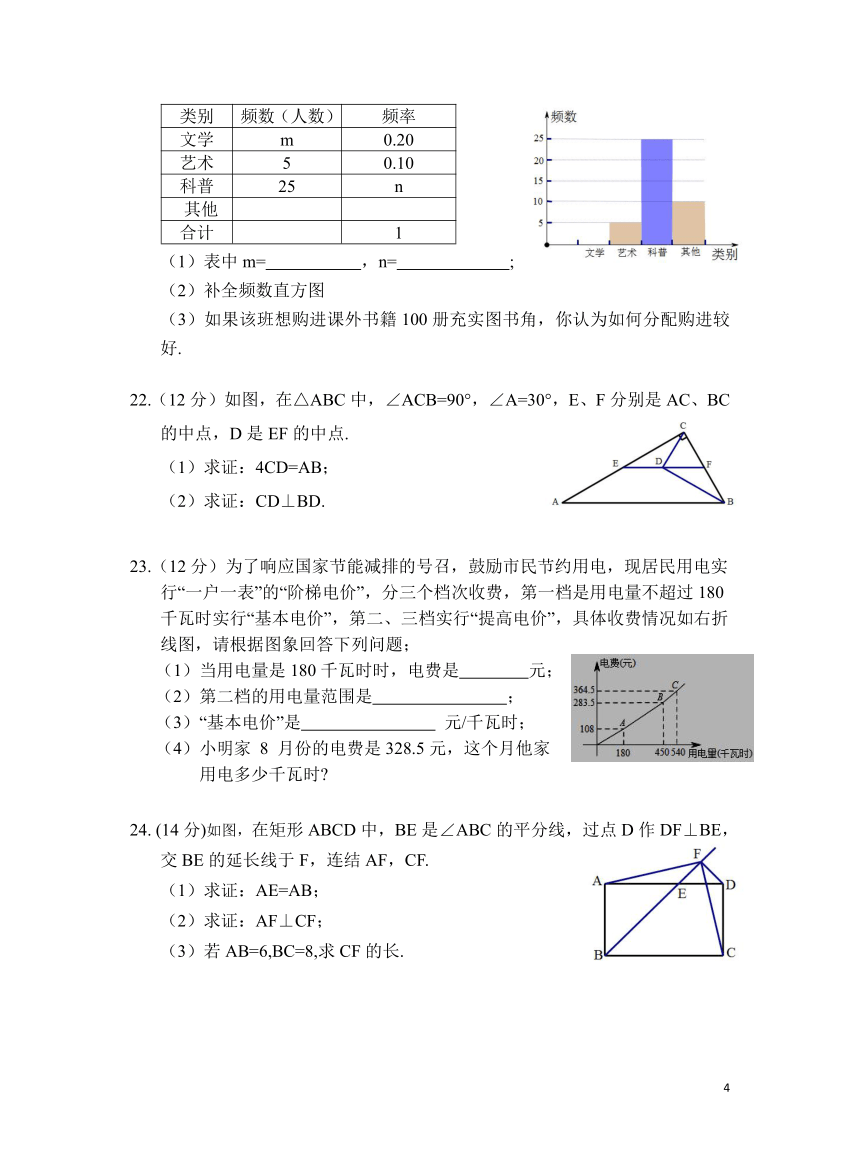
21.(12分)某中学为了解八年级某班学生的课外阅读情况,就“我最喜爱的课外读物”从“文学”、“艺术”、“科普”和“其它”四个类别进行了调查(每位同学仅选一项),并根据调查结果制作了下表和频数直方图:
类别 频数(人数) 频率
文学 m 0.20
艺术 5 0.10
科普 25 n
其他
合计 1
(1)表中m= ,n= ;
(2)补全频数直方图
(3)如果该班想购进课外书籍100册充实图书角,你认为如何分配购进较好.
22.(12分)如图,在△ABC中,∠ACB=90°,∠A=30°,E、F分别是AC、BC的中点,D是EF的中点.
求证:4CD=AB;
求证:CD⊥BD.
23.(12分)为了响应国家节能减排的号召,鼓励市民节约用电,现居民用电实行“一户一表”的“阶梯电价”,分三个档次收费,第一档是用电量不超过180千瓦时实行“基本电价”,第二、三档实行“提高电价”,具体收费情况如右折线图,请根据图象回答下列问题;
(1)当用电量是180千瓦时时,电费是 元;
(2)第二档的用电量范围是 ;
(3)“基本电价”是 元/千瓦时;
(4)小明家 8 月份的电费是328.5元,这个月他家
用电多少千瓦时
24. (14分)如图,在矩形ABCD中,BE是∠ABC的平分线,过点D作DF⊥BE,交BE的延长线于F,连结AF,CF.
(1)求证:AE=AB;
(2)求证:AF⊥CF;
(3)若AB=6,BC=8,求CF的长.
2023年八年级期末试卷
数学参考答案
一、选择题(4分×10,共40分)
1——10:BABAC CCDAD
二、填空题(4分×6,共24分)
,12. 34.6米 ,13. 24 ,14. ,15. 4 ,
(-2,3)或(2,-3)或(6,3)
三、解答题
(8分)
A(-1,-1),B(-3,-2),C(-3,-1)(3分)
画出正确图形(2分),(3)画出正确图形(3分)
(8分)
证明:∵AD是△ABC的高,且AD=BD
∴∠DBA=∠DAB=45°
又∵∠BAC=80°
∴∠DAC=∠BAC-∠DAB=80°-45°
=35°
在Rt△BDE与Rt△ADC中
∴Rt△BDE≌Rt△ADC (HL)
∴∠DBE=∠DAC=35°
(10分)
解:(1)设过A(-2,1),B(1,4)的直线的解析式是:
∴
解得:
∴直线的表达式是
(2)
=
∴△OAB的面积是
(10分)
解:(1)在 ABCD中,AD//BC
∴∠ABC+∠A=180°
又∵∠ABC=70°
∠A=180°-∠ABC=110°
∠D=∠ABC=70°
(2)在 ABCD中,AD//BC
∴∠AEB=∠CBE
又∵BE平分∠ABC
∴∠ABE=∠CBE
∴∠ABE=∠AEB
∴AB=AE
又∵AB=3,DE=1
∴AD=4
ABCD的周长=2(AB+AD)
=2(3+4)=14
(12分)
解:(1)m=10 ,n=0.5
(2)补全图形
文学类:100×0.2=20(册),艺术类:100×0.1=10(册)
科普类:100×0.5=50(册),其他:100×0.2=20(册)
(12分)
(1)证明:在△ABC中,E、F分别是AC、BC的中点
∴ EF//AB,且AB=2EF
∴∠CEF=∠A
∵ ∠A=30°
∴∠CEF=30°
∵∠ACB=90°
又∵D是EF的中点
∴EF=2CD
∴4CD=AB
(2)由(1)知∠CEF=30°,CD=CF=DF
∴∠CDF=∠CFD=60°
又点F是CB的中点
∴DF=BF
∴∠BDF=∠DBF=
∴∠CDB=∠CDF+∠BDF
=60°+30°=90°
∴ CD⊥BD
(12分)
解:(1)108
(2)大于180千瓦时而小于或等于450千瓦时
(3)0.6
(4)328.5元已属于第三档“提高电价”
设电费用(元)表示,用电量用(千瓦时)表示,
则第三档电价收费的表达式是:
由图知(450,283.5),(540,364.5)在直线上
∴
解得
∴第三档电费的表达式是:
∴
∴(千瓦时)
答: 8 月份小明家用电500千瓦时.
24.(14分)
(1)求证:在矩形ABCD中,BE是∠ABC的平分线
∴∠ABE=∠CBE=45°
又AD//BC
∴∠AEB=∠CBF
∴∠ABE=∠AEB=45°
∴AE=AB
(2)∵∠FED=∠AEB=45°
又DF⊥BF
∴∠FDE=FED=45°
∴FD=FE
∴∠FDC=∠FEA=135°
由(1)知CD=BA=EA
∴△FDC≌△FEA (SAS)
∴∠DFC=∠EFA
∵∠DFC+∠CFB=∠DFB=90°
∴∠EFA+∠CFB=90°
即AF⊥CF
(3)连结AC
∵AB=6,BC=8
∴AC=
=10
由(2)知△FDC≌△FEA,且AF⊥CF
∴FC=FA
由(2)知AF⊥CF
∴FC2+FA2=AC2
∴2CF2=AC2=102
∴CF=
1
数 学
温馨提示:
(1)本学科试卷分试题卷和答题卷两部分,考试时量为120分钟,满分为150分.
(2)请你将姓名、准考证号等相关信息按要求填涂在答题卡上.
(3)请你按答题卡要求,在答题卡上作答,答在本试题卷上无效.
一、选择题(每小题4分,共40分)
1、直角三角形的一锐角是40°,那么另一锐角是( )
A. 40° B. 50° C. 60° D.70°
2、一个多边形的内角和为1440°,那么这个多边形是( )
A.十边形 B.九边形 C.八边形 D.七边形
3、点P(-2,3)关于x轴对称的点是( )
A.(2,3) B. (-2,-3) C.(2,-3) D. (3,-2)
4、 下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
5、下列函数是关于自变量的一次函数的是( )
A. B. C. D.
6、抛掷两枚质量和形状相同的硬币,则出现“一正一反”的频率是( )
A.1 B. C. D.
如图,在△ABC中,∠C=90°,AC=BC,AD是角平分线,CD=,那么AB的长是( )
A. B.
C. D.
8、正比例函数的函数值随的增大而减小,则一次函数的图象大致是( ).
9、下列命题中,真命题是( )
A. 对角线互相平分的四边形是平行四边形
B. 有一组邻边相等且对角线互相垂直的四边形是菱形
C. 有一个角是直角且对角线相等的四边形是矩形
D. 对角线互相垂直平分的四边形是正方形
10、一个四边形的边长依次是,b,c,d且满足,则这个四边形是( )
A. 矩形 B. 菱形 C.正方形 D. 平行四边形
二、填空题(每小题4分,共24分)
11、函数中自变量的取值范围是 ;
如图,为了测量古塔的高,小明在点A测得看古塔顶点C
处的仰角为30°,然后向古塔方向前进到40米的点B处测
得古塔顶点C的仰角是60°,A、B、D在同一直线上,那
么古塔CD的高是 米.(,结果保留一位小数)
如图,在菱形ABCD中,边AB=5,对角线AC=6,那么,
这个菱形ABCD的面积是 ;
14、已知一次函数的图形经过第一、三、四象限,那么,的取值范围是___________.
15、如图,两个边长为4的正方形部分重叠在一起,点O是一个
正方形的中心,另一个正方形的顶点与点O重合,并绕着O
点旋转,那么重叠部分的面积是 ;
16、如图,在平面直角坐标系中,已知点A(4,0)和
点B(2,3),A、B、O、D四点是平行四边形的顶点,
那么点D的坐标是 .
二、解答题(共86分)
17、(8分)如图,在平面直角坐标系中,△ABC的顶点都在网格点上. 写出A、B、C三点的坐标;
画出△ABC关于y轴的对称图形△A1B1C1;
画出把△ABC向右平移五个单位长度,然后再
向上平移四个单位长度的图形△A2B2C2.
18.(8分)如图,AD是△ABC的高,AD=BD,BE=AC,∠BAC=80°.求∠DBE的度数.
19、(10分)如图,平面直角坐标系中,直线经过点A(-2,1)和点B(1,4).
求直线的表达式;
求△OAB的面积.
20.(10分)如图,在□ABCD中,∠ABC=70°,BE平分∠ABC,交AD于E,AB=3cm,ED=1cm.
求∠A,∠C,∠D的度数;
求□ABCD的周长.
21.(12分)某中学为了解八年级某班学生的课外阅读情况,就“我最喜爱的课外读物”从“文学”、“艺术”、“科普”和“其它”四个类别进行了调查(每位同学仅选一项),并根据调查结果制作了下表和频数直方图:
类别 频数(人数) 频率
文学 m 0.20
艺术 5 0.10
科普 25 n
其他
合计 1
(1)表中m= ,n= ;
(2)补全频数直方图
(3)如果该班想购进课外书籍100册充实图书角,你认为如何分配购进较好.
22.(12分)如图,在△ABC中,∠ACB=90°,∠A=30°,E、F分别是AC、BC的中点,D是EF的中点.
求证:4CD=AB;
求证:CD⊥BD.
23.(12分)为了响应国家节能减排的号召,鼓励市民节约用电,现居民用电实行“一户一表”的“阶梯电价”,分三个档次收费,第一档是用电量不超过180千瓦时实行“基本电价”,第二、三档实行“提高电价”,具体收费情况如右折线图,请根据图象回答下列问题;
(1)当用电量是180千瓦时时,电费是 元;
(2)第二档的用电量范围是 ;
(3)“基本电价”是 元/千瓦时;
(4)小明家 8 月份的电费是328.5元,这个月他家
用电多少千瓦时
24. (14分)如图,在矩形ABCD中,BE是∠ABC的平分线,过点D作DF⊥BE,交BE的延长线于F,连结AF,CF.
(1)求证:AE=AB;
(2)求证:AF⊥CF;
(3)若AB=6,BC=8,求CF的长.
2023年八年级期末试卷
数学参考答案
一、选择题(4分×10,共40分)
1——10:BABAC CCDAD
二、填空题(4分×6,共24分)
,12. 34.6米 ,13. 24 ,14. ,15. 4 ,
(-2,3)或(2,-3)或(6,3)
三、解答题
(8分)
A(-1,-1),B(-3,-2),C(-3,-1)(3分)
画出正确图形(2分),(3)画出正确图形(3分)
(8分)
证明:∵AD是△ABC的高,且AD=BD
∴∠DBA=∠DAB=45°
又∵∠BAC=80°
∴∠DAC=∠BAC-∠DAB=80°-45°
=35°
在Rt△BDE与Rt△ADC中
∴Rt△BDE≌Rt△ADC (HL)
∴∠DBE=∠DAC=35°
(10分)
解:(1)设过A(-2,1),B(1,4)的直线的解析式是:
∴
解得:
∴直线的表达式是
(2)
=
∴△OAB的面积是
(10分)
解:(1)在 ABCD中,AD//BC
∴∠ABC+∠A=180°
又∵∠ABC=70°
∠A=180°-∠ABC=110°
∠D=∠ABC=70°
(2)在 ABCD中,AD//BC
∴∠AEB=∠CBE
又∵BE平分∠ABC
∴∠ABE=∠CBE
∴∠ABE=∠AEB
∴AB=AE
又∵AB=3,DE=1
∴AD=4
ABCD的周长=2(AB+AD)
=2(3+4)=14
(12分)
解:(1)m=10 ,n=0.5
(2)补全图形
文学类:100×0.2=20(册),艺术类:100×0.1=10(册)
科普类:100×0.5=50(册),其他:100×0.2=20(册)
(12分)
(1)证明:在△ABC中,E、F分别是AC、BC的中点
∴ EF//AB,且AB=2EF
∴∠CEF=∠A
∵ ∠A=30°
∴∠CEF=30°
∵∠ACB=90°
又∵D是EF的中点
∴EF=2CD
∴4CD=AB
(2)由(1)知∠CEF=30°,CD=CF=DF
∴∠CDF=∠CFD=60°
又点F是CB的中点
∴DF=BF
∴∠BDF=∠DBF=
∴∠CDB=∠CDF+∠BDF
=60°+30°=90°
∴ CD⊥BD
(12分)
解:(1)108
(2)大于180千瓦时而小于或等于450千瓦时
(3)0.6
(4)328.5元已属于第三档“提高电价”
设电费用(元)表示,用电量用(千瓦时)表示,
则第三档电价收费的表达式是:
由图知(450,283.5),(540,364.5)在直线上
∴
解得
∴第三档电费的表达式是:
∴
∴(千瓦时)
答: 8 月份小明家用电500千瓦时.
24.(14分)
(1)求证:在矩形ABCD中,BE是∠ABC的平分线
∴∠ABE=∠CBE=45°
又AD//BC
∴∠AEB=∠CBF
∴∠ABE=∠AEB=45°
∴AE=AB
(2)∵∠FED=∠AEB=45°
又DF⊥BF
∴∠FDE=FED=45°
∴FD=FE
∴∠FDC=∠FEA=135°
由(1)知CD=BA=EA
∴△FDC≌△FEA (SAS)
∴∠DFC=∠EFA
∵∠DFC+∠CFB=∠DFB=90°
∴∠EFA+∠CFB=90°
即AF⊥CF
(3)连结AC
∵AB=6,BC=8
∴AC=
=10
由(2)知△FDC≌△FEA,且AF⊥CF
∴FC=FA
由(2)知AF⊥CF
∴FC2+FA2=AC2
∴2CF2=AC2=102
∴CF=
1
同课章节目录
