2.4.2圆的一般方程课件-2022-2023学年高二上学期数学人教A版(2019)选择性必修第一册(共17张PPT)
文档属性
| 名称 | 2.4.2圆的一般方程课件-2022-2023学年高二上学期数学人教A版(2019)选择性必修第一册(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 650.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-03 13:11:20 | ||
图片预览






文档简介
(共17张PPT)
2.4.2
圆的一般方程
人教A版(2019)选择性必修第一册
学习目标
1. 掌握圆的一般方程、及其推导过程与特点。
2. 会根据圆的一般方程写出圆的半径和圆心坐标。
3.会根据给定的条件求圆的一般方程,并且能用圆的一般方程解决有关问题。
4.核心素养:逻辑推理、数学抽象、数学运算
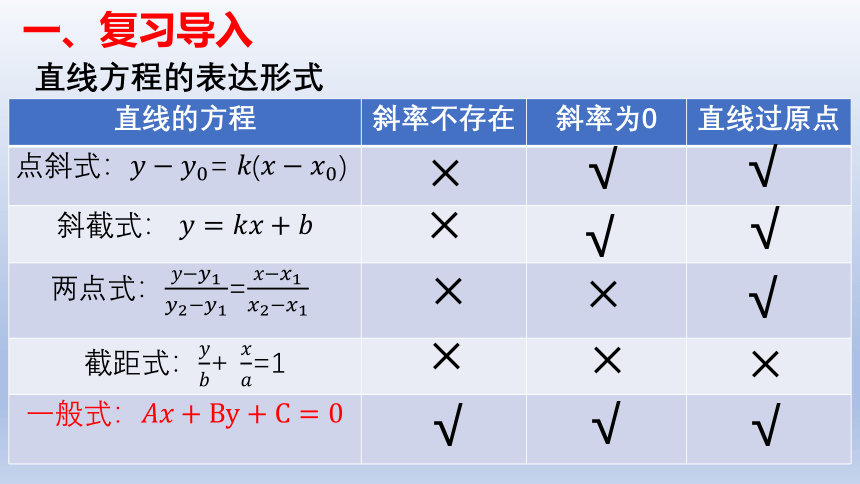
一、复习导入
直线方程的表达形式
直线的方程 斜率不存在 斜率为0 直线过原点
点斜式:= ()
斜截式:
两点式:=
截距式:+=1
一般式:
×
√
√
×
√
√
×
×
√
×
×
×
√
√
√
问题1:类比直线方程的研究过程,圆的方程是否也有一般式?
二、新课讲授
1、圆的一般方程
将括号打开,得到形如:
追问1:方程 是否表示圆?
配方得到:
0,
0,
0,
(-,- ),半径.
(-,- ).
解,不表示任何图形.
当>0时,我们把方程 叫做圆的一般方程.
问题2:圆的标准方程与圆的一般方程各有什么特点呢?
标准方程 一般方程
方程
代数特征
系数
圆心
半径
的二元二次方程
>0
例1 判断下列方程表示什么图形,并说明理由.
(1)
(2)
三、巩固新知
分析:法①:配方,转化为标准方程,找圆心半径
法②:直接用公式>0来判断
解(1):
(1)式变形为
表示圆心为(1,-2),半径为的圆
(2)法一:
(2)式变形为
当≠0时,
表示圆心为(- ,0),半径为的圆
当=0时,
表示点(0,0)
(2)法二:
由圆的一般式方程 ,得
2 ,=0, =- ,
则=4 +4 ≥0
当>0时,
表示圆心为(- ,0),半径为的圆
当=0时,
表示点(0,0)
例2 求过三点, ,的圆的方程,并求这个圆的圆心坐标和半径.
解:设圆的方程为 ,
待定系数法
因为点在圆上,故它们都满足方程,则
解得
所以圆的一般方程为: ,
圆心为(4,-3),半径为.
小结:待定系数法
标准方程:
①参量:( )、
②三元二次方程组
一般方程:
①参量:、
②三元一次方程组
更加适合用待定系数法
问题3:什么是待定系数法?如何运用待定系数法求圆的方程呢?
一般先写出含有未知系数的解的形式(如一种类型的方法、算式或表达式),然后再根据问题所给的条件解得所设的未知系数.由于其中的系数是未知和待定的,这类方法就被称为待定系数法.
(1)根据题意,选择标准方程或一般方程;
(2)根据条件列出关于 或,的方程组;
(3)解出 或,,得到标准方程或一般方程.
变式训练 已知四点, ,, ,问这四个点是否在同一个圆上.
解:设过点的圆的方程为 ,则
解得
所以圆的一般方程为: ,
将点代入圆的方程得:
左右两边相等,故在圆上.
分析:解法二
1, -1
为过, 的圆的直径
求出半径,得到圆的标准方程
将点代入方程,判断其是否在圆上
例3 已知线段的端点的坐标为端点在圆上运动,求线段的中点的轨迹方程.
分析:如何理解轨迹和轨迹方程
直线:在平面直角坐标系中,与定点连线的倾斜角为定值的点的集合.
圆:在平面直角坐标系中,到定点的距离等于定长的点的集合.
轨迹:符合一定规则的点集.
轨迹方程:点的坐标所满足的方程.
A
B
M
解:设过点,则有
,
于是有, ①
由于在圆上,故有
4
把①式代入得:
4
整理得
这就是点的轨迹方程,它表示以(, )为圆心,半径为1的圆.
小结:
已知定曲线上一动点,动点与存在某种关系,求动点的轨迹方程.
方法:用从动点坐标表示主动点坐标,代入给定的曲线方程.
四、课堂小结
1、圆的一般方程:
五、作业布置
课本P88:练习 第2、3题
2、从数入手,用好待定系数法、方程思想.
3、求动点的轨迹方程.
2.4.2
圆的一般方程
人教A版(2019)选择性必修第一册
学习目标
1. 掌握圆的一般方程、及其推导过程与特点。
2. 会根据圆的一般方程写出圆的半径和圆心坐标。
3.会根据给定的条件求圆的一般方程,并且能用圆的一般方程解决有关问题。
4.核心素养:逻辑推理、数学抽象、数学运算
一、复习导入
直线方程的表达形式
直线的方程 斜率不存在 斜率为0 直线过原点
点斜式:= ()
斜截式:
两点式:=
截距式:+=1
一般式:
×
√
√
×
√
√
×
×
√
×
×
×
√
√
√
问题1:类比直线方程的研究过程,圆的方程是否也有一般式?
二、新课讲授
1、圆的一般方程
将括号打开,得到形如:
追问1:方程 是否表示圆?
配方得到:
0,
0,
0,
(-,- ),半径.
(-,- ).
解,不表示任何图形.
当>0时,我们把方程 叫做圆的一般方程.
问题2:圆的标准方程与圆的一般方程各有什么特点呢?
标准方程 一般方程
方程
代数特征
系数
圆心
半径
的二元二次方程
>0
例1 判断下列方程表示什么图形,并说明理由.
(1)
(2)
三、巩固新知
分析:法①:配方,转化为标准方程,找圆心半径
法②:直接用公式>0来判断
解(1):
(1)式变形为
表示圆心为(1,-2),半径为的圆
(2)法一:
(2)式变形为
当≠0时,
表示圆心为(- ,0),半径为的圆
当=0时,
表示点(0,0)
(2)法二:
由圆的一般式方程 ,得
2 ,=0, =- ,
则=4 +4 ≥0
当>0时,
表示圆心为(- ,0),半径为的圆
当=0时,
表示点(0,0)
例2 求过三点, ,的圆的方程,并求这个圆的圆心坐标和半径.
解:设圆的方程为 ,
待定系数法
因为点在圆上,故它们都满足方程,则
解得
所以圆的一般方程为: ,
圆心为(4,-3),半径为.
小结:待定系数法
标准方程:
①参量:( )、
②三元二次方程组
一般方程:
①参量:、
②三元一次方程组
更加适合用待定系数法
问题3:什么是待定系数法?如何运用待定系数法求圆的方程呢?
一般先写出含有未知系数的解的形式(如一种类型的方法、算式或表达式),然后再根据问题所给的条件解得所设的未知系数.由于其中的系数是未知和待定的,这类方法就被称为待定系数法.
(1)根据题意,选择标准方程或一般方程;
(2)根据条件列出关于 或,的方程组;
(3)解出 或,,得到标准方程或一般方程.
变式训练 已知四点, ,, ,问这四个点是否在同一个圆上.
解:设过点的圆的方程为 ,则
解得
所以圆的一般方程为: ,
将点代入圆的方程得:
左右两边相等,故在圆上.
分析:解法二
1, -1
为过, 的圆的直径
求出半径,得到圆的标准方程
将点代入方程,判断其是否在圆上
例3 已知线段的端点的坐标为端点在圆上运动,求线段的中点的轨迹方程.
分析:如何理解轨迹和轨迹方程
直线:在平面直角坐标系中,与定点连线的倾斜角为定值的点的集合.
圆:在平面直角坐标系中,到定点的距离等于定长的点的集合.
轨迹:符合一定规则的点集.
轨迹方程:点的坐标所满足的方程.
A
B
M
解:设过点,则有
,
于是有, ①
由于在圆上,故有
4
把①式代入得:
4
整理得
这就是点的轨迹方程,它表示以(, )为圆心,半径为1的圆.
小结:
已知定曲线上一动点,动点与存在某种关系,求动点的轨迹方程.
方法:用从动点坐标表示主动点坐标,代入给定的曲线方程.
四、课堂小结
1、圆的一般方程:
五、作业布置
课本P88:练习 第2、3题
2、从数入手,用好待定系数法、方程思想.
3、求动点的轨迹方程.
