沪科版数学九年级上册 第23章检测卷2(含答案)
文档属性
| 名称 | 沪科版数学九年级上册 第23章检测卷2(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 537.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-04 10:19:40 | ||
图片预览




文档简介
第23章达标检测卷
(150分,120分钟)
一、选择题(每题4分,共40分)
1.在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tanB的值是( )
A. B.3 C. D.2
2.在△ABC中,∠C=90°,AB=5,BC=3,则cosA的值是( )
A. B. C. D.
3.如果∠为锐角,且sin=0.6,那么的取值范围是( )
A.0°<≤30° B.30°<<45° C.45°<<60° D.60°<≤90°
4.若为锐角,且sin=,则tan的值为( )
A. B. C. D.
5.如图,在平面直角坐标系中,P是第一象限内的点,其坐标为(3,m),且OP与x轴正半轴的夹角的正切值是,则sin的值为( )
A. B. C. D.
第5题图 第8题图 第9题图 第10题图
6. 在Rt△ABC中,∠C=90°,sinB=,则cosA的值为( )
A. B. C. D.
7.在△ABC中,∠A=120°,AB=4,AC=2,则sinB的值是( )
A. B. C. D.
8.如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AC于点E,则tan∠CDE的值等于( )
A. B. C. D.
9.如图,两条宽度均为40 m的公路相交成角,那么这两条公路在相交处的公共部分(图中阴影部分)的路面面积是( )
A.(m2) B.(m2) C.1600sin(m2) D.1600cos(m2)
10.如图,一个小球由地面沿着坡度i=1:2的坡面向上前进了10m,此时小球距离地面的高度为( )
A.5m B.m C.4m D.2
二、填空题(每题5分,共20分)
11.如图,在四边形ABCD中,∠BAD=30°,∠C=90°,∠ADB=105°,sin∠BDC=,AD=4.则DC=___________.
第11题图 第12题图 第13题图 第14题图
12.如图,在A处看建筑物CD的顶端D的仰角为,且tan=0.7,向前行进3米到达B处,从B处看D的仰角为45°(图中各点均在同一平面内,A、B、C三点在同一条直线上,CD⊥AC),则建筑物CD的高度为___________米.
13.如图,已知点A(5,0),直线y=x+b(b>0)与x轴、y轴分别相交于点C、B,连接AB,∠=75°,则b=________.
14.如图,正方形ABCD中,E是CD中点,FC=BC,则tan∠EAF=________.
三、解答题(15~18题每题8分,19,20题每题10分,21,22题每题12分,23题14分,共90分)
15.计算:(1)+2sin45°-;
(2)sin30°tan60°-(-tan45)2016+.
16.如图,在△ABC中,BD⊥AC于点D,AB=6,AC=5,∠A=30°.
(1)求BD和AD的长;
(2)求tanC的值.
17.如图,某中学课外活动小组的同学利用所学知识去测量某河段的宽度.小明同学在A处观测对岸C点,测得∠CAD=45°,小英同学在距A处50米远的B处测得∠CBD=30°,请你根据这些数据计算出河宽.(精确到0.01米,参考数据:≈1.414,≈1.732)
18.如图,在Rt△ABC中,∠C=90°,M是直角边AC上一点,MN⊥AB于点N,AN=3,AM=4,求tanB的值.
19.如图,已知Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.
(1)求sinB的值;
(2)如果CD=,求BE的值.
20.已知,△ABC中,D是BC上的一点,且∠DAC=30°,过点D作ED⊥AD交AC于点E,AE=4,EC=2.
(1)求证:AD=CD;
(2)若tanB=3,求线段AB的长﹒
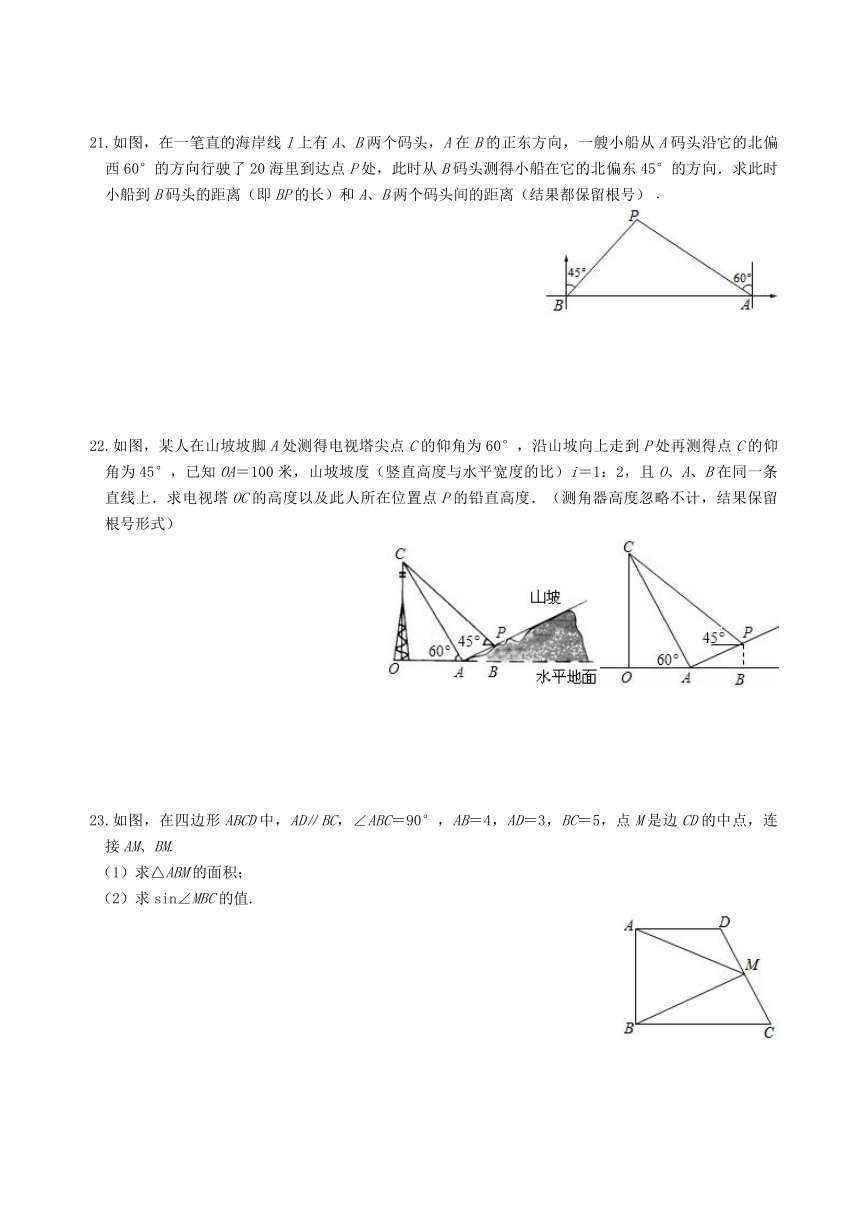
21.如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号)﹒
22.如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100米,山坡坡度(竖直高度与水平宽度的比)i=1:2,且O、A、B在同一条直线上.求电视塔OC的高度以及此人所在位置点P的铅直高度.(测角器高度忽略不计,结果保留根号形式)
23.如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=4,AD=3,BC=5,点M是边CD的中点,连接AM、BM.
(1)求△ABM的面积;
(2)求sin∠MBC的值.
参考答案
1.D 2.D 3.B 4.D 5.A 6.C 7.B 8.C 9.A 10.D 11. 12.7 13.5 14.
15. 解:(1)+2sin45°-;
=+2×-,
=+-
=+-2+2
=3-.
(2)sin30°tan60°-(-tan45)2016+.
=×-(-1)2016+
=-1+1-
=.
16.解:(1)∵BD⊥AC,AB=6,∠A=30°,
∴BD=AB=3,
在Rt△ABD中,AD=ABcosA=6×=3.
(2)∵AC=5,AD=3,
∴CD=AC-AD=2,
在Rt△BCD中,tanC===.
17.解:过C作CE⊥AB于E,设CE=x米,
在Rt△AEC中:∠CAE=45°,
∴AE=CE=x
在Rt△BCE中,∠CBE=30°,BE=CE=x,
∵BE=AE+AB,
∴x=x+50,
解得:x=25+25≈68.30.
答:河宽为68.30米.
18.解:∵∠C=90°,MN⊥AB,
∴∠C=∠ANM=90°,
又∵∠MAN=∠BAC,
∴△AMN∽△ABC,
∴==,
设AC=3x,AB=4x,
由勾股定理得:BC==,
在Rt△ABC中,tanB===.
19.解:(1)∵∠ACB=90°,CD是斜边AB上的中线,
∴CD=BD,
∴∠B=∠BCD,
∵AE⊥CD,
∴∠CAH+∠ACH=90°,
又∠ACB=90°,
∴∠BCD+∠ACH=90°,
∴∠B=∠BCD=∠CAH,即∠B=∠CAH,
∵AH=2CH,
∴由勾股定理得AC=CH,
∴CH:AC=1:,
∴sinB=.
(2)∵sinB=,
∴AC:AB=1:,
∴AC=2,
∵∠CAH=∠B,
∴sin∠CAH=sinB=,
设CE=x(x>0),则AE=x,则x2+22=(x)2,
∴CE=x=1,AC=2,
在Rt△ABC中,AC2+BC2=AB2,
∵AB=2CD=2,
∴BC=4,
∴BE=BC-CE=3.
20.(1)证明:∵ED⊥AD,
∴∠ADE=90°.
在Rt△ADE中,∠DAE=30°,AE=4,
∴∠DEA=60°,DE=AE=2,
∵EC=2,
∴DE=EC,
∴∠EDC=∠C.
又∵∠EDC+∠C=∠DEA=60°,
∴∠C=30°=∠DAE,
∴AD=CD.
(2)解:如图,过点A作AF⊥BC于点F,则∠AFC=∠AFB=90°,
∵AE=4,EC=2,
∴AC=6.
在Rt△AFC中,∠AFC=90°,∠C=30°,
∴AF=AC=3.
在Rt△AFB中,∠AFB=90°,tanB=3,
∴BF==1,
∴AB==.
21.解:过P作PM⊥AB于M,
则∠PMB=∠PMA=90°,
∵∠PBM=90°﹣45°=45°,∠PAM=90°﹣60°=30°,AP=20海里,
∴PM=AP=10海里,AM=APcos30°=10海里,
∴∠BPM=∠PBM=45°,
∴PM=BM=10海里,
∴AB=AM+BM=(10+10)海里,
∴BP==10海里,
即小船到B码头的距离是10海里,A、B两个码头间的距离是(10+10)海里.
22.解:作PE⊥OB于点E,PF⊥CO于点F,
在Rt△AOC中,AO=100,∠CAO=60°,
∴CO=AOtan60°=100(米).
设PE=x米,
∵tan∠PAB==,
∴AE=2x.
在Rt△PCF中,∠CPF=45°,
CF=100﹣x,PF=OA+AE=100+2x,
∵PF=CF,
∴100+2x=100﹣x,
解得x=(米),
答:电视塔OC高为100米,点P的铅直高度为(米).
23.解:(1)延长AM交BC的延长线于点N,
∵AD∥BC,
∴∠DAM=∠N,∠D=∠MCN.
∵点M是边CD的中点,
∴DM=CM,
∴△ADM≌△NCM(AAS),
∴CN=AD=3,AM=MN=AN,
∴BN=BC+CN=5+3=8.
∵∠ABC=90°,
∴S△ABN=×ABBN=×4×8=16,
∴S△ABM=S△ABN=8,
∴△ABM的面积为8.
(2)过点M作MK⊥BC,
∵∠ABC=90°,
∴MK∥AB,
∴△NMK∽△NAB,
∴==,
∴MK=AB=2,
在Rt△ABN中,AN===4,
∴BM=AN=2,
在Rt△BKM中,sin∠MBC===,
∴∠MBC的正弦值为.
(150分,120分钟)
一、选择题(每题4分,共40分)
1.在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tanB的值是( )
A. B.3 C. D.2
2.在△ABC中,∠C=90°,AB=5,BC=3,则cosA的值是( )
A. B. C. D.
3.如果∠为锐角,且sin=0.6,那么的取值范围是( )
A.0°<≤30° B.30°<<45° C.45°<<60° D.60°<≤90°
4.若为锐角,且sin=,则tan的值为( )
A. B. C. D.
5.如图,在平面直角坐标系中,P是第一象限内的点,其坐标为(3,m),且OP与x轴正半轴的夹角的正切值是,则sin的值为( )
A. B. C. D.
第5题图 第8题图 第9题图 第10题图
6. 在Rt△ABC中,∠C=90°,sinB=,则cosA的值为( )
A. B. C. D.
7.在△ABC中,∠A=120°,AB=4,AC=2,则sinB的值是( )
A. B. C. D.
8.如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AC于点E,则tan∠CDE的值等于( )
A. B. C. D.
9.如图,两条宽度均为40 m的公路相交成角,那么这两条公路在相交处的公共部分(图中阴影部分)的路面面积是( )
A.(m2) B.(m2) C.1600sin(m2) D.1600cos(m2)
10.如图,一个小球由地面沿着坡度i=1:2的坡面向上前进了10m,此时小球距离地面的高度为( )
A.5m B.m C.4m D.2
二、填空题(每题5分,共20分)
11.如图,在四边形ABCD中,∠BAD=30°,∠C=90°,∠ADB=105°,sin∠BDC=,AD=4.则DC=___________.
第11题图 第12题图 第13题图 第14题图
12.如图,在A处看建筑物CD的顶端D的仰角为,且tan=0.7,向前行进3米到达B处,从B处看D的仰角为45°(图中各点均在同一平面内,A、B、C三点在同一条直线上,CD⊥AC),则建筑物CD的高度为___________米.
13.如图,已知点A(5,0),直线y=x+b(b>0)与x轴、y轴分别相交于点C、B,连接AB,∠=75°,则b=________.
14.如图,正方形ABCD中,E是CD中点,FC=BC,则tan∠EAF=________.
三、解答题(15~18题每题8分,19,20题每题10分,21,22题每题12分,23题14分,共90分)
15.计算:(1)+2sin45°-;
(2)sin30°tan60°-(-tan45)2016+.
16.如图,在△ABC中,BD⊥AC于点D,AB=6,AC=5,∠A=30°.
(1)求BD和AD的长;
(2)求tanC的值.
17.如图,某中学课外活动小组的同学利用所学知识去测量某河段的宽度.小明同学在A处观测对岸C点,测得∠CAD=45°,小英同学在距A处50米远的B处测得∠CBD=30°,请你根据这些数据计算出河宽.(精确到0.01米,参考数据:≈1.414,≈1.732)
18.如图,在Rt△ABC中,∠C=90°,M是直角边AC上一点,MN⊥AB于点N,AN=3,AM=4,求tanB的值.
19.如图,已知Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.
(1)求sinB的值;
(2)如果CD=,求BE的值.
20.已知,△ABC中,D是BC上的一点,且∠DAC=30°,过点D作ED⊥AD交AC于点E,AE=4,EC=2.
(1)求证:AD=CD;
(2)若tanB=3,求线段AB的长﹒
21.如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号)﹒
22.如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100米,山坡坡度(竖直高度与水平宽度的比)i=1:2,且O、A、B在同一条直线上.求电视塔OC的高度以及此人所在位置点P的铅直高度.(测角器高度忽略不计,结果保留根号形式)
23.如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=4,AD=3,BC=5,点M是边CD的中点,连接AM、BM.
(1)求△ABM的面积;
(2)求sin∠MBC的值.
参考答案
1.D 2.D 3.B 4.D 5.A 6.C 7.B 8.C 9.A 10.D 11. 12.7 13.5 14.
15. 解:(1)+2sin45°-;
=+2×-,
=+-
=+-2+2
=3-.
(2)sin30°tan60°-(-tan45)2016+.
=×-(-1)2016+
=-1+1-
=.
16.解:(1)∵BD⊥AC,AB=6,∠A=30°,
∴BD=AB=3,
在Rt△ABD中,AD=ABcosA=6×=3.
(2)∵AC=5,AD=3,
∴CD=AC-AD=2,
在Rt△BCD中,tanC===.
17.解:过C作CE⊥AB于E,设CE=x米,
在Rt△AEC中:∠CAE=45°,
∴AE=CE=x
在Rt△BCE中,∠CBE=30°,BE=CE=x,
∵BE=AE+AB,
∴x=x+50,
解得:x=25+25≈68.30.
答:河宽为68.30米.
18.解:∵∠C=90°,MN⊥AB,
∴∠C=∠ANM=90°,
又∵∠MAN=∠BAC,
∴△AMN∽△ABC,
∴==,
设AC=3x,AB=4x,
由勾股定理得:BC==,
在Rt△ABC中,tanB===.
19.解:(1)∵∠ACB=90°,CD是斜边AB上的中线,
∴CD=BD,
∴∠B=∠BCD,
∵AE⊥CD,
∴∠CAH+∠ACH=90°,
又∠ACB=90°,
∴∠BCD+∠ACH=90°,
∴∠B=∠BCD=∠CAH,即∠B=∠CAH,
∵AH=2CH,
∴由勾股定理得AC=CH,
∴CH:AC=1:,
∴sinB=.
(2)∵sinB=,
∴AC:AB=1:,
∴AC=2,
∵∠CAH=∠B,
∴sin∠CAH=sinB=,
设CE=x(x>0),则AE=x,则x2+22=(x)2,
∴CE=x=1,AC=2,
在Rt△ABC中,AC2+BC2=AB2,
∵AB=2CD=2,
∴BC=4,
∴BE=BC-CE=3.
20.(1)证明:∵ED⊥AD,
∴∠ADE=90°.
在Rt△ADE中,∠DAE=30°,AE=4,
∴∠DEA=60°,DE=AE=2,
∵EC=2,
∴DE=EC,
∴∠EDC=∠C.
又∵∠EDC+∠C=∠DEA=60°,
∴∠C=30°=∠DAE,
∴AD=CD.
(2)解:如图,过点A作AF⊥BC于点F,则∠AFC=∠AFB=90°,
∵AE=4,EC=2,
∴AC=6.
在Rt△AFC中,∠AFC=90°,∠C=30°,
∴AF=AC=3.
在Rt△AFB中,∠AFB=90°,tanB=3,
∴BF==1,
∴AB==.
21.解:过P作PM⊥AB于M,
则∠PMB=∠PMA=90°,
∵∠PBM=90°﹣45°=45°,∠PAM=90°﹣60°=30°,AP=20海里,
∴PM=AP=10海里,AM=APcos30°=10海里,
∴∠BPM=∠PBM=45°,
∴PM=BM=10海里,
∴AB=AM+BM=(10+10)海里,
∴BP==10海里,
即小船到B码头的距离是10海里,A、B两个码头间的距离是(10+10)海里.
22.解:作PE⊥OB于点E,PF⊥CO于点F,
在Rt△AOC中,AO=100,∠CAO=60°,
∴CO=AOtan60°=100(米).
设PE=x米,
∵tan∠PAB==,
∴AE=2x.
在Rt△PCF中,∠CPF=45°,
CF=100﹣x,PF=OA+AE=100+2x,
∵PF=CF,
∴100+2x=100﹣x,
解得x=(米),
答:电视塔OC高为100米,点P的铅直高度为(米).
23.解:(1)延长AM交BC的延长线于点N,
∵AD∥BC,
∴∠DAM=∠N,∠D=∠MCN.
∵点M是边CD的中点,
∴DM=CM,
∴△ADM≌△NCM(AAS),
∴CN=AD=3,AM=MN=AN,
∴BN=BC+CN=5+3=8.
∵∠ABC=90°,
∴S△ABN=×ABBN=×4×8=16,
∴S△ABM=S△ABN=8,
∴△ABM的面积为8.
(2)过点M作MK⊥BC,
∵∠ABC=90°,
∴MK∥AB,
∴△NMK∽△NAB,
∴==,
∴MK=AB=2,
在Rt△ABN中,AN===4,
∴BM=AN=2,
在Rt△BKM中,sin∠MBC===,
∴∠MBC的正弦值为.
