平方差公式[上学期]
图片预览


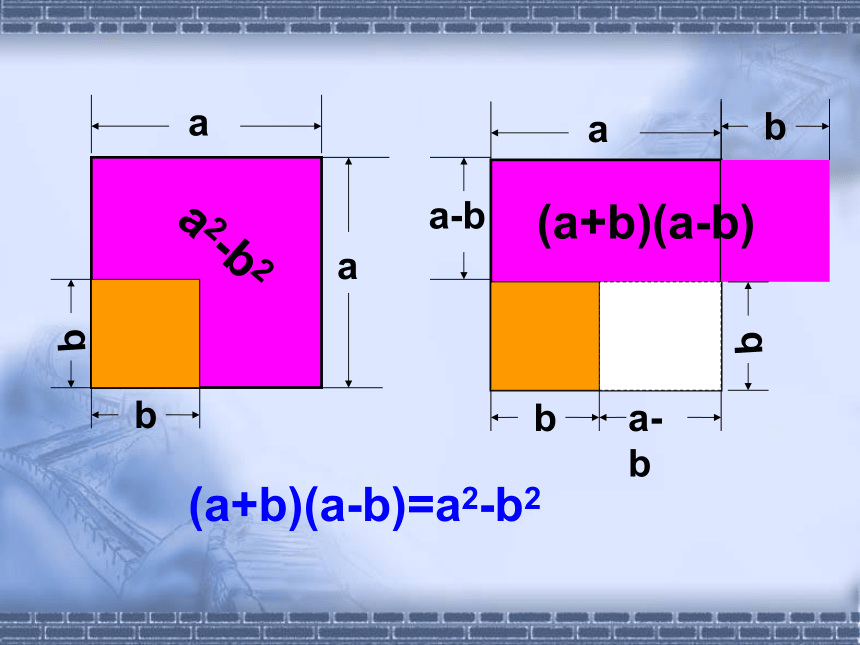
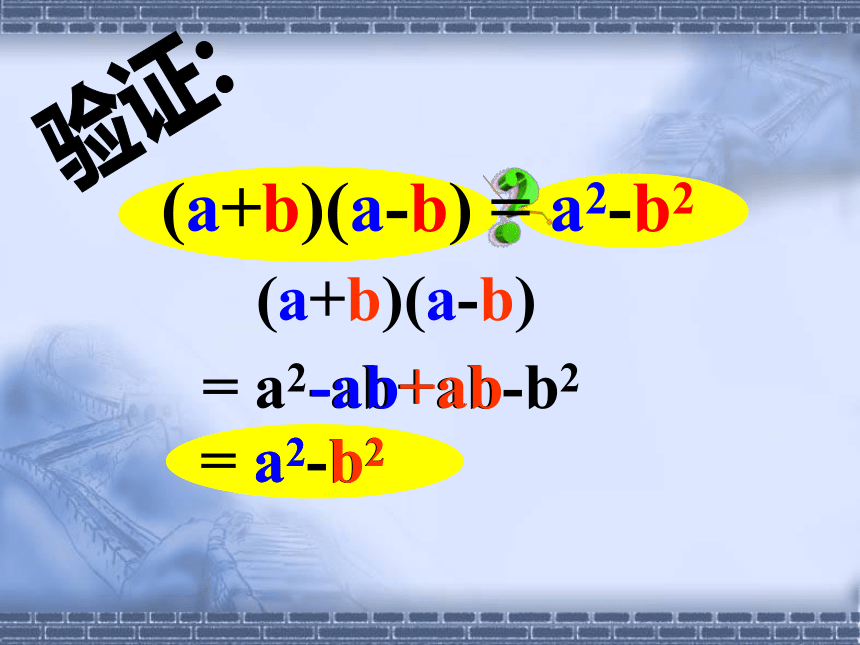

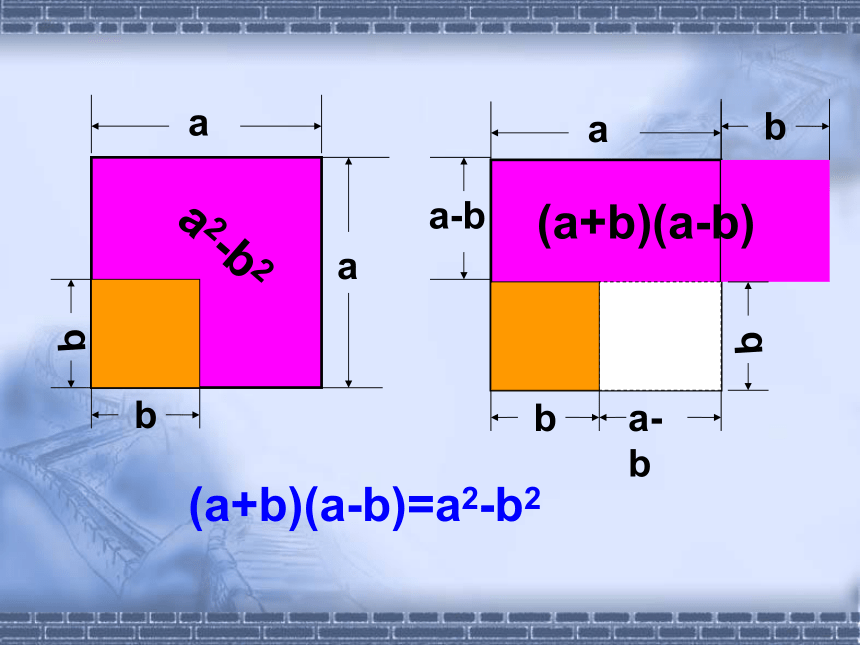

文档简介
课件29张PPT。飞厦中学 杜冕雯复习:计算下列多项式的积: (x+1)(x-1) =
(m+2)(m-2) =
(2x+1)(2x-1) =x2 - 1m2 - 44x2 - 1 (3x)2 = ______
(- 4x)2 = ______9x216x2 a2-b2(a+b)(a-b)(a+b)(a-b)=a2-b2(a+b)(a-b) = a2-b2
验证:(a+b)(a-b)= a2-ab+ab-b2-ab+ab= a2-b2a2b2(a+b)(a-b)=a2-b2
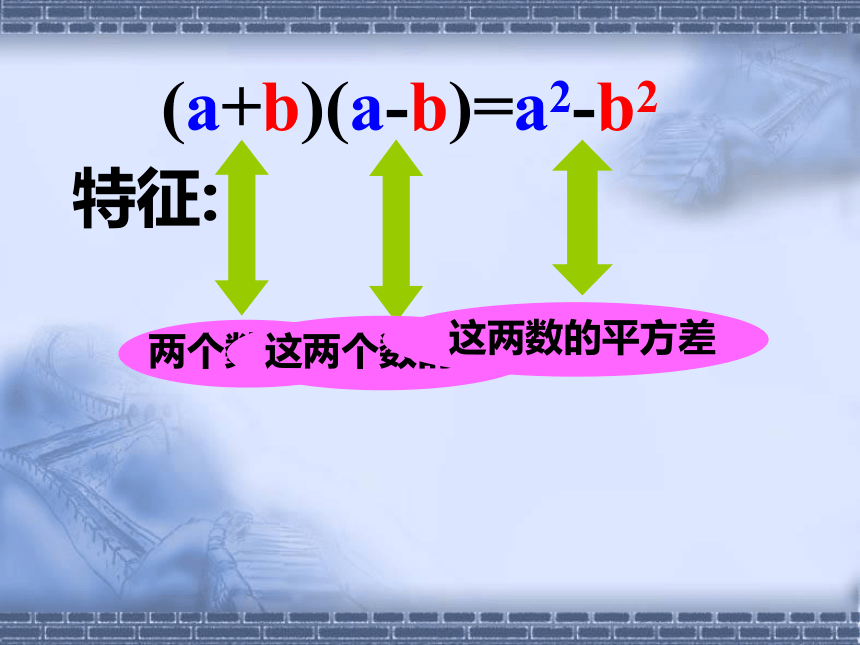
两个数的和与这两个数的差的积,
等于这两个数的平方差. §15.3.1 平方差公式 a2-b2(a+b)(a-b)(a+b)(a-b)=a2-b2(a+b)(a-b)=a2-b2
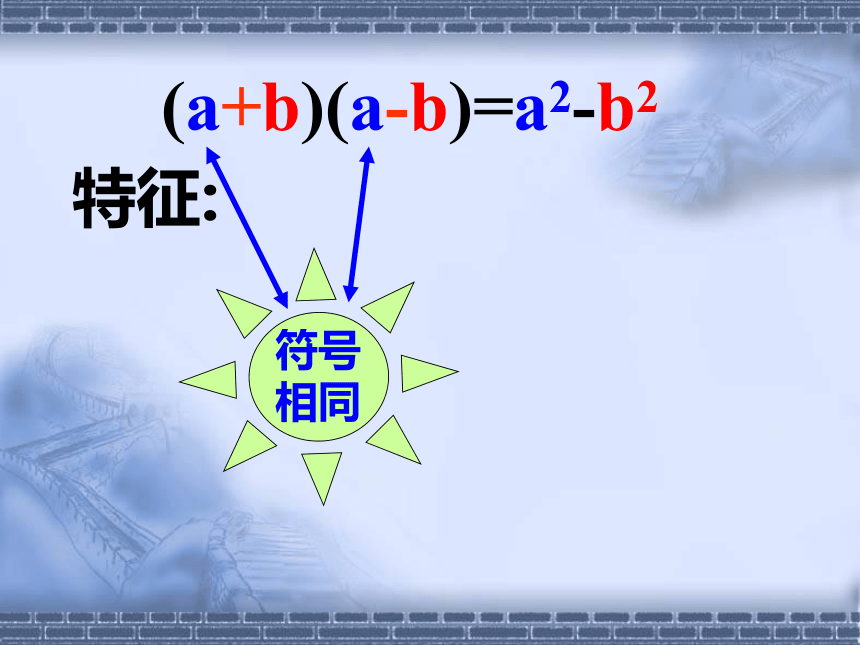
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
说明: 公式中的a,b可以表示具体的数(正数或负数),也可以表示一个单项式或一个多项式.选择下列各式中,能用平方差公式运算的是( )
A.(-a+b)(-a-b) B.(a-b)(b-a)
C.(2a-3b)(3a+2b) D.(a-b+c)(b-a-c)
2.下列各式相乘,不能用平方差公式计算的是( )
A.(x-2y)(2y+x) B.(-x+2y)(-x-2y)
C.(-2y-x)(x+2y) D.(-2b-5)(2b-5)AC例1 运用平方差公式计算:1、( 3x + 2 )( 3x – 2 ) ; 2、( b + 2a )( 2a – b ); 3、( -x + 2y )( -x - 2y ). 分析: ⑴ (3x+2)(3x-2) 3x3xaa22bb= a2 - b2=(3x)2-22用公式关键是识别两数
符号相同的项 a
符号相反的项 b解: ⑴ (3x+2)(3x-2) =(3x)2 3x3x-2222= 9x2 - 4⑵ (b+2a)(2a-b);b-b+2a2a= (2a+b)(2a-b)2a2a= (2a)2 = 4a2 – b2bb-b2 (3) (-x+2y)(-x-2y) = (-x)2-(2y)2= x2-4y2ㄨ判断 下面各式的计算对不对?
如果不对,应当怎样改正?(1) (x+2)(x-2) = x2 - 2 (2) (-3a-2)(3a-2) = 9a2 - 4 X2 - 4ㄨ4 - 9a2填空 运用平方差公式计算:a2 - 9b2(2) (3+2a)(-3+2a) = 4a2 - 9小试牛刀例2 计算:⑴ 102 ×98;⑵ (y+2)(y-2)-(y-1)(y+5);⑴ 102 ×98102= (100+2)98(100-2)= 1002-22= 10000-4= 9996⑵ (y+2)(y-2)-(y-1)(y+5)yyyy22= y2 - 2215- (y2+4y-5)= y2-4-y2-4y+5= -4y+1我能行!运用平方差公式计算:1、(p+q)(-q+p) =
2、(-x-y) (x-y) =
3、(2a+b)(2a-b) =
4、(x2+y2)(x2-y2)=
5、 51 × 49 =
p2-q2y2-x24a2-b2x4-y42499(a+b)(a-b)=a2-b2
挑战极限 (2+1)(22+1)(24+1)(28+1) … (22n+1) 运用平方差公式计算:挑战极限王二小同学在计算(2+1)(22+1)(24+1)时,
将积式乘以(2-1)得:
解:原式 = (2-1)(2+1)(22+1)(24+1) = (22-1)(22+1)(24+1)= (24-1)(24+1)= 28-1挑战极限你能根据上题计算:
(2+1)(22+1)(24+1)(28+1) … (22n+1)
的结果吗? 24n-1平方差公式(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积,
等于这两个数的平方差.小结P 184
1. (3) ﹑(4)、 (5) ﹑(6)作业
(m+2)(m-2) =
(2x+1)(2x-1) =x2 - 1m2 - 44x2 - 1 (3x)2 = ______
(- 4x)2 = ______9x216x2 a2-b2(a+b)(a-b)(a+b)(a-b)=a2-b2(a+b)(a-b) = a2-b2
验证:(a+b)(a-b)= a2-ab+ab-b2-ab+ab= a2-b2a2b2(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积,
等于这两个数的平方差. §15.3.1 平方差公式 a2-b2(a+b)(a-b)(a+b)(a-b)=a2-b2(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
说明: 公式中的a,b可以表示具体的数(正数或负数),也可以表示一个单项式或一个多项式.选择下列各式中,能用平方差公式运算的是( )
A.(-a+b)(-a-b) B.(a-b)(b-a)
C.(2a-3b)(3a+2b) D.(a-b+c)(b-a-c)
2.下列各式相乘,不能用平方差公式计算的是( )
A.(x-2y)(2y+x) B.(-x+2y)(-x-2y)
C.(-2y-x)(x+2y) D.(-2b-5)(2b-5)AC例1 运用平方差公式计算:1、( 3x + 2 )( 3x – 2 ) ; 2、( b + 2a )( 2a – b ); 3、( -x + 2y )( -x - 2y ). 分析: ⑴ (3x+2)(3x-2) 3x3xaa22bb= a2 - b2=(3x)2-22用公式关键是识别两数
符号相同的项 a
符号相反的项 b解: ⑴ (3x+2)(3x-2) =(3x)2 3x3x-2222= 9x2 - 4⑵ (b+2a)(2a-b);b-b+2a2a= (2a+b)(2a-b)2a2a= (2a)2 = 4a2 – b2bb-b2 (3) (-x+2y)(-x-2y) = (-x)2-(2y)2= x2-4y2ㄨ判断 下面各式的计算对不对?
如果不对,应当怎样改正?(1) (x+2)(x-2) = x2 - 2 (2) (-3a-2)(3a-2) = 9a2 - 4 X2 - 4ㄨ4 - 9a2填空 运用平方差公式计算:a2 - 9b2(2) (3+2a)(-3+2a) = 4a2 - 9小试牛刀例2 计算:⑴ 102 ×98;⑵ (y+2)(y-2)-(y-1)(y+5);⑴ 102 ×98102= (100+2)98(100-2)= 1002-22= 10000-4= 9996⑵ (y+2)(y-2)-(y-1)(y+5)yyyy22= y2 - 2215- (y2+4y-5)= y2-4-y2-4y+5= -4y+1我能行!运用平方差公式计算:1、(p+q)(-q+p) =
2、(-x-y) (x-y) =
3、(2a+b)(2a-b) =
4、(x2+y2)(x2-y2)=
5、 51 × 49 =
p2-q2y2-x24a2-b2x4-y42499(a+b)(a-b)=a2-b2
挑战极限 (2+1)(22+1)(24+1)(28+1) … (22n+1) 运用平方差公式计算:挑战极限王二小同学在计算(2+1)(22+1)(24+1)时,
将积式乘以(2-1)得:
解:原式 = (2-1)(2+1)(22+1)(24+1) = (22-1)(22+1)(24+1)= (24-1)(24+1)= 28-1挑战极限你能根据上题计算:
(2+1)(22+1)(24+1)(28+1) … (22n+1)
的结果吗? 24n-1平方差公式(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积,
等于这两个数的平方差.小结P 184
1. (3) ﹑(4)、 (5) ﹑(6)作业
