人教版八年级上册11.3.2多边形的内角和教案(表格版)
文档属性
| 名称 | 人教版八年级上册11.3.2多边形的内角和教案(表格版) |
|
|
| 格式 | doc | ||
| 文件大小 | 65.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-04 00:00:00 | ||
图片预览


文档简介
多边形的内角和
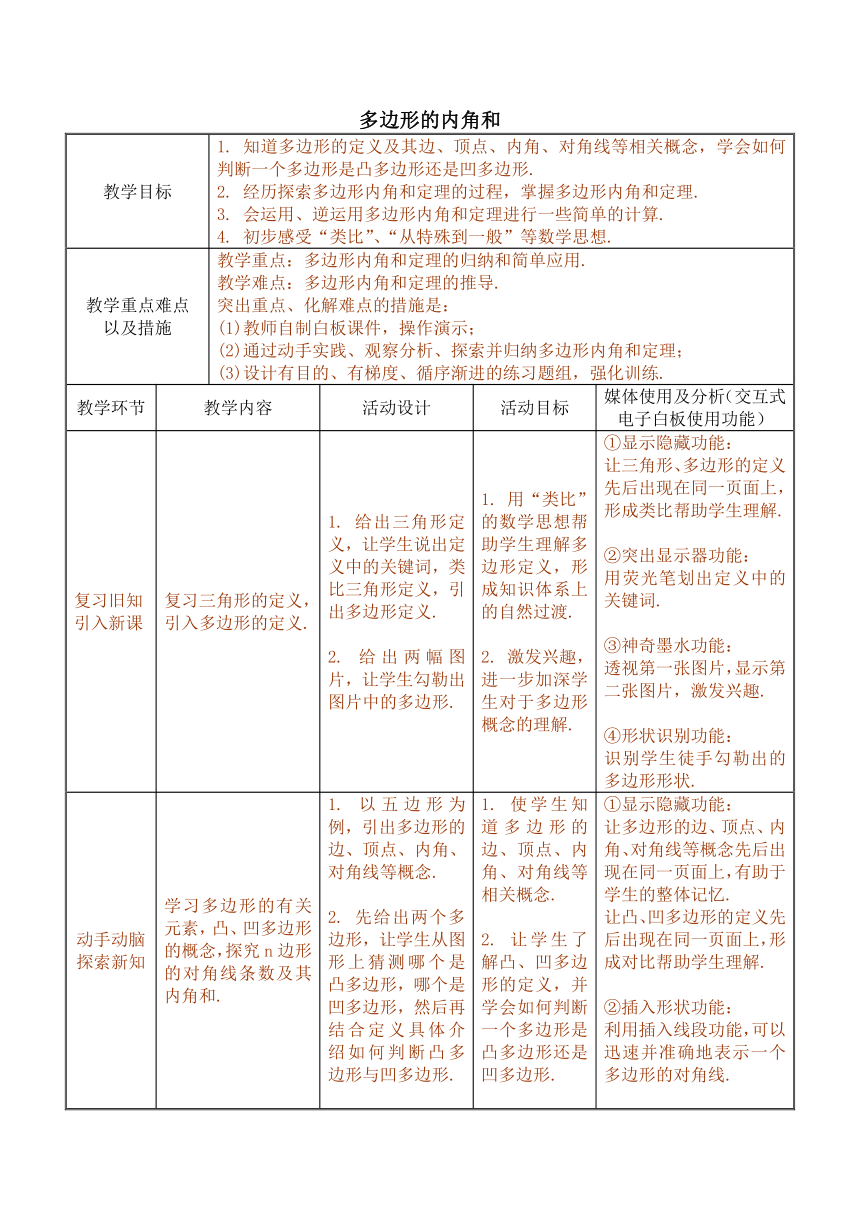
教学目标 1. 知道多边形的定义及其边、顶点、内角、对角线等相关概念,学会如何判断一个多边形是凸多边形还是凹多边形.2. 经历探索多边形内角和定理的过程,掌握多边形内角和定理.3. 会运用、逆运用多边形内角和定理进行一些简单的计算.4. 初步感受“类比”、“从特殊到一般”等数学思想.
教学重点难点以及措施 教学重点:多边形内角和定理的归纳和简单应用.教学难点:多边形内角和定理的推导.突出重点、化解难点的措施是:(1)教师自制白板课件,操作演示;(2)通过动手实践、观察分析、探索并归纳多边形内角和定理;(3)设计有目的、有梯度、循序渐进的练习题组,强化训练.
教学环节 教学内容 活动设计 活动目标 媒体使用及分析(交互式电子白板使用功能)
复习旧知引入新课 复习三角形的定义,引入多边形的定义. 1. 给出三角形定义,让学生说出定义中的关键词,类比三角形定义,引出多边形定义.2. 给出两幅图片,让学生勾勒出图片中的多边形. 1. 用“类比”的数学思想帮助学生理解多边形定义,形成知识体系上的自然过渡.2. 激发兴趣,进一步加深学生对于多边形概念的理解. ①显示隐藏功能:让三角形、多边形的定义先后出现在同一页面上,形成类比帮助学生理解.②突出显示器功能:用荧光笔划出定义中的关键词.③神奇墨水功能:透视第一张图片,显示第二张图片,激发兴趣.④形状识别功能:识别学生徒手勾勒出的多边形形状.
动手动脑探索新知 学习多边形的有关元素,凸、凹多边形的概念,探究n边形的对角线条数及其内角和. 1. 以五边形为例,引出多边形的边、顶点、内角、对角线等概念.2. 先给出两个多边形,让学生从图形上猜测哪个是凸多边形,哪个是凹多边形,然后再结合定义具体介绍如何判断凸多边形与凹多边形.3. 练一练.(学生口答、上台操作、动手实践)4. 填写表格,从特殊到一般,探究n边形从一个顶点出发的对角线条数和总的对角线条数与n的关系.5. 继续填写另一张表格,从“把多边形分割成若干个三角形”的角度探究n边形的内角和与n的关系,得到初步的结论:n边形的内角和=(n-2)×180°.6. 想一想:上述的分割方法是否唯一?让学生动手尝试,然后展示其他两种分割方法,同样可以得到相同的结论,继而引出多边形的内角和定理. 1. 使学生知道多边形的边、顶点、内角、对角线等相关概念.2. 让学生了解凸、凹多边形的定义,并学会如何判断一个多边形是凸多边形还是凹多边形.3. 对之前所学的内容进行一个小检测.4. 通过师生合作探究,让学生理解n边形从一个顶点出发的对角线条数和总的对角线条数与n之间的关系.5. 还是通过师生合作探究,由学生归纳出n边形的内角和与n的关系.6. 通过动手实践,让学生明白多边形内角和公式的推导方法并不唯一,进一步加深对该公式的理解. ①显示隐藏功能:让多边形的边、顶点、内角、对角线等概念先后出现在同一页面上,有助于学生的整体记忆.让凸、凹多边形的定义先后出现在同一页面上,形成对比帮助学生理解.②插入形状功能:利用插入线段功能,可以迅速并准确地表示一个多边形的对角线.③数学标尺功能:利用标尺功能配合笔工具,能准确地画出多边形任意一边所在直线,有助学生理解凸、凹多边形的区别.④橡皮擦除功能:在事先做好的表格上利用橡皮擦除功能,直接“擦出”正确答案.⑤显露器功能:在“想一想”这一环节,利用显露器功能逐一显示三种不同的多边形分割方法,有助于学生集中注意力,也方便教师逐一进行分析和讲解.
例题讲解练习巩固 主讲两道很典型的多边形内角和例题,引导学生完成八道课堂练习题. 1. 例题1:一个多边形共有20条对角线,问:(1)这个多边形是几边形?(2)该多边形的内角和是多少度?2. 例题2:如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.3. 课堂练习. 1. 直接运用n边形总的对角线条数及其内角和与n的关系解决问题.2. 学会如何将不在同一多边形内的若干个角转换到同一个多边形内进而求解. 此外,本题解法并不唯一,可以拓宽学生的解题思路.3. 对本节课所学内容进行反馈和巩固. ①即时书写功能:例题1和例题2均用到了即时书写功能,教师直接将解题过程写在了页面上,此时白板代替了原有的黑板.②插入形状功能:例题2有一种解法需要添加辅助线,此时可利用插入虚线段的功能,作出辅助线,规范解题过程.③即时标注功能:有些几何题需要在图形上进行标注,如本课例2中线段AB和线段EF所成的角、线段CD和线段EF所成的角都可以利用笔工具进行即时标注,方便教师进行讲解.
思维拓展拼图游戏(根据时间而定) 探究有关“n边形截去一个角”的问题,利用白板功能完成一个趣味小游戏. 1. 拓展练习:把五边形剪去一个角,将得到几边形?此时多边形的内角和有什么变化?追问:若把n边形剪去一个角呢?2. 变式练习:一个多边形截去一个角后,形成另一个多边形的内角和为1800°,你知道原多边形有多少条边吗?3. 干扰练习.4. 拼图游戏.5. 数学欣赏——多边形的镶嵌. 1. 培养学生多角度思考问题的能力和数学归纳能力.2. 进一步巩固此类题型.3. 设置陷阱,帮助学生更好地区分题型,达到举一反三的效果.4. 以游戏的形式简单渗透多边形镶嵌这一课外知识.5. 以卢浮宫为例,体现数学在生活中的应用. ①显示隐藏功能:拓展练习中将三种情况事先做好隐藏起来,学生说到哪一种就显示哪一种,灵活应对.②即时书写功能:变式练习采用即时书写功能,从而规范此类题型的解题过程.③文字前置功能:干扰练习中将解答过程事先做好,文字颜色设置成白色并前置,然后拖动彩色的矩形框呈现答案,清晰明了,节约时间.④拖动副本功能:拼图游戏中用到了拖动副本功能,学生可以反复调用多个图形从而完成自己理想中的拼图.
课堂小结布置作业 整理并小结本节课所学的知识点,布置个性化作业. 1. 课堂小结:(1)多边形的定义;(2)多边形中的有关元素;(3)凸多边形和凹多边形;(4)多边形的内角和定理.2. 布置作业:(1)个性化22.1第一课时;(2)预习多边形的外角和. 1. 依次呈现本节课所学习的知识点,并设置几个判断性的问题帮助学生进一步巩固所学知识.2. 布置个性化作业,为多边形的外角和做好铺垫. ①显示隐藏功能采用显示隐藏功能依次呈现本节课所学习的知识点,层次分明.②即时标注功能对小结中所呈现的判断性语句进行即时地圈划,指明错误所在,解决学生可能潜在的一些疑惑.
(附)课堂练习:
1. 下列角度中,不能成为多边形内角和的只有( ).
A. 540° B. 680° C. 1800° D. 900°
2. 凸n边形的内角中,锐角的个数最多有( )个.
A. 1 B. 2 C. 3 D. 4
3. 如果设n边形的内角和为f(n),那么f(n)=________,它是n的________函数,f(12)=________.
4. 若一个多边形从一个顶点出发的对角线有7条,则该多边形是________边形,它共有________条对角线.
5. 若一个多边形的内角和是720度,那么这个多边形从一个顶点出发的对角线有________条.
6. 一个多边形的边数如果增加一条,那么它的内角和增加的度数为________度.
7. 在五边形ABCDE中,如果∠A和∠D都是直角,且∠B:∠C:∠E=3:8:7,则∠E的度数为________.
8. 如果一个多边形的每个内角都等于144°,则这个多边形是正________边形.
教学反思:
我对本节课的反思如下:
1、教的转变
本节课教师的角色从知识的传授者转变为学生学习的组织者、引导者、合作者与共同研究者,利用电子白板直观地展示,激发学生自觉探究数学问题,体验发现的乐趣.
2、学的转变
学生的角色从学会转变为会学. 本节课学生不是停留在学会课本知识层面,而是站在研究者的角度深入其境.
3、课堂氛围的转变
整节课以“流畅、开放、合作、‘隐’导”为基本特征,教师对学生的思维减少干预,教学过程呈现一种比较流畅的特征. 整节课学生与学生,学生与教师之间以“对话”、“讨论”为出发点,以互助合作为手段,以解决问题为目的,让学生在一个比较宽松的环境中自主选择获得成功的方向,判断发现的价值.
教学目标 1. 知道多边形的定义及其边、顶点、内角、对角线等相关概念,学会如何判断一个多边形是凸多边形还是凹多边形.2. 经历探索多边形内角和定理的过程,掌握多边形内角和定理.3. 会运用、逆运用多边形内角和定理进行一些简单的计算.4. 初步感受“类比”、“从特殊到一般”等数学思想.
教学重点难点以及措施 教学重点:多边形内角和定理的归纳和简单应用.教学难点:多边形内角和定理的推导.突出重点、化解难点的措施是:(1)教师自制白板课件,操作演示;(2)通过动手实践、观察分析、探索并归纳多边形内角和定理;(3)设计有目的、有梯度、循序渐进的练习题组,强化训练.
教学环节 教学内容 活动设计 活动目标 媒体使用及分析(交互式电子白板使用功能)
复习旧知引入新课 复习三角形的定义,引入多边形的定义. 1. 给出三角形定义,让学生说出定义中的关键词,类比三角形定义,引出多边形定义.2. 给出两幅图片,让学生勾勒出图片中的多边形. 1. 用“类比”的数学思想帮助学生理解多边形定义,形成知识体系上的自然过渡.2. 激发兴趣,进一步加深学生对于多边形概念的理解. ①显示隐藏功能:让三角形、多边形的定义先后出现在同一页面上,形成类比帮助学生理解.②突出显示器功能:用荧光笔划出定义中的关键词.③神奇墨水功能:透视第一张图片,显示第二张图片,激发兴趣.④形状识别功能:识别学生徒手勾勒出的多边形形状.
动手动脑探索新知 学习多边形的有关元素,凸、凹多边形的概念,探究n边形的对角线条数及其内角和. 1. 以五边形为例,引出多边形的边、顶点、内角、对角线等概念.2. 先给出两个多边形,让学生从图形上猜测哪个是凸多边形,哪个是凹多边形,然后再结合定义具体介绍如何判断凸多边形与凹多边形.3. 练一练.(学生口答、上台操作、动手实践)4. 填写表格,从特殊到一般,探究n边形从一个顶点出发的对角线条数和总的对角线条数与n的关系.5. 继续填写另一张表格,从“把多边形分割成若干个三角形”的角度探究n边形的内角和与n的关系,得到初步的结论:n边形的内角和=(n-2)×180°.6. 想一想:上述的分割方法是否唯一?让学生动手尝试,然后展示其他两种分割方法,同样可以得到相同的结论,继而引出多边形的内角和定理. 1. 使学生知道多边形的边、顶点、内角、对角线等相关概念.2. 让学生了解凸、凹多边形的定义,并学会如何判断一个多边形是凸多边形还是凹多边形.3. 对之前所学的内容进行一个小检测.4. 通过师生合作探究,让学生理解n边形从一个顶点出发的对角线条数和总的对角线条数与n之间的关系.5. 还是通过师生合作探究,由学生归纳出n边形的内角和与n的关系.6. 通过动手实践,让学生明白多边形内角和公式的推导方法并不唯一,进一步加深对该公式的理解. ①显示隐藏功能:让多边形的边、顶点、内角、对角线等概念先后出现在同一页面上,有助于学生的整体记忆.让凸、凹多边形的定义先后出现在同一页面上,形成对比帮助学生理解.②插入形状功能:利用插入线段功能,可以迅速并准确地表示一个多边形的对角线.③数学标尺功能:利用标尺功能配合笔工具,能准确地画出多边形任意一边所在直线,有助学生理解凸、凹多边形的区别.④橡皮擦除功能:在事先做好的表格上利用橡皮擦除功能,直接“擦出”正确答案.⑤显露器功能:在“想一想”这一环节,利用显露器功能逐一显示三种不同的多边形分割方法,有助于学生集中注意力,也方便教师逐一进行分析和讲解.
例题讲解练习巩固 主讲两道很典型的多边形内角和例题,引导学生完成八道课堂练习题. 1. 例题1:一个多边形共有20条对角线,问:(1)这个多边形是几边形?(2)该多边形的内角和是多少度?2. 例题2:如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.3. 课堂练习. 1. 直接运用n边形总的对角线条数及其内角和与n的关系解决问题.2. 学会如何将不在同一多边形内的若干个角转换到同一个多边形内进而求解. 此外,本题解法并不唯一,可以拓宽学生的解题思路.3. 对本节课所学内容进行反馈和巩固. ①即时书写功能:例题1和例题2均用到了即时书写功能,教师直接将解题过程写在了页面上,此时白板代替了原有的黑板.②插入形状功能:例题2有一种解法需要添加辅助线,此时可利用插入虚线段的功能,作出辅助线,规范解题过程.③即时标注功能:有些几何题需要在图形上进行标注,如本课例2中线段AB和线段EF所成的角、线段CD和线段EF所成的角都可以利用笔工具进行即时标注,方便教师进行讲解.
思维拓展拼图游戏(根据时间而定) 探究有关“n边形截去一个角”的问题,利用白板功能完成一个趣味小游戏. 1. 拓展练习:把五边形剪去一个角,将得到几边形?此时多边形的内角和有什么变化?追问:若把n边形剪去一个角呢?2. 变式练习:一个多边形截去一个角后,形成另一个多边形的内角和为1800°,你知道原多边形有多少条边吗?3. 干扰练习.4. 拼图游戏.5. 数学欣赏——多边形的镶嵌. 1. 培养学生多角度思考问题的能力和数学归纳能力.2. 进一步巩固此类题型.3. 设置陷阱,帮助学生更好地区分题型,达到举一反三的效果.4. 以游戏的形式简单渗透多边形镶嵌这一课外知识.5. 以卢浮宫为例,体现数学在生活中的应用. ①显示隐藏功能:拓展练习中将三种情况事先做好隐藏起来,学生说到哪一种就显示哪一种,灵活应对.②即时书写功能:变式练习采用即时书写功能,从而规范此类题型的解题过程.③文字前置功能:干扰练习中将解答过程事先做好,文字颜色设置成白色并前置,然后拖动彩色的矩形框呈现答案,清晰明了,节约时间.④拖动副本功能:拼图游戏中用到了拖动副本功能,学生可以反复调用多个图形从而完成自己理想中的拼图.
课堂小结布置作业 整理并小结本节课所学的知识点,布置个性化作业. 1. 课堂小结:(1)多边形的定义;(2)多边形中的有关元素;(3)凸多边形和凹多边形;(4)多边形的内角和定理.2. 布置作业:(1)个性化22.1第一课时;(2)预习多边形的外角和. 1. 依次呈现本节课所学习的知识点,并设置几个判断性的问题帮助学生进一步巩固所学知识.2. 布置个性化作业,为多边形的外角和做好铺垫. ①显示隐藏功能采用显示隐藏功能依次呈现本节课所学习的知识点,层次分明.②即时标注功能对小结中所呈现的判断性语句进行即时地圈划,指明错误所在,解决学生可能潜在的一些疑惑.
(附)课堂练习:
1. 下列角度中,不能成为多边形内角和的只有( ).
A. 540° B. 680° C. 1800° D. 900°
2. 凸n边形的内角中,锐角的个数最多有( )个.
A. 1 B. 2 C. 3 D. 4
3. 如果设n边形的内角和为f(n),那么f(n)=________,它是n的________函数,f(12)=________.
4. 若一个多边形从一个顶点出发的对角线有7条,则该多边形是________边形,它共有________条对角线.
5. 若一个多边形的内角和是720度,那么这个多边形从一个顶点出发的对角线有________条.
6. 一个多边形的边数如果增加一条,那么它的内角和增加的度数为________度.
7. 在五边形ABCDE中,如果∠A和∠D都是直角,且∠B:∠C:∠E=3:8:7,则∠E的度数为________.
8. 如果一个多边形的每个内角都等于144°,则这个多边形是正________边形.
教学反思:
我对本节课的反思如下:
1、教的转变
本节课教师的角色从知识的传授者转变为学生学习的组织者、引导者、合作者与共同研究者,利用电子白板直观地展示,激发学生自觉探究数学问题,体验发现的乐趣.
2、学的转变
学生的角色从学会转变为会学. 本节课学生不是停留在学会课本知识层面,而是站在研究者的角度深入其境.
3、课堂氛围的转变
整节课以“流畅、开放、合作、‘隐’导”为基本特征,教师对学生的思维减少干预,教学过程呈现一种比较流畅的特征. 整节课学生与学生,学生与教师之间以“对话”、“讨论”为出发点,以互助合作为手段,以解决问题为目的,让学生在一个比较宽松的环境中自主选择获得成功的方向,判断发现的价值.
