数学人教A版(2019)选择性必修第一册3.1.1椭圆及其标准方程 课件(共19张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册3.1.1椭圆及其标准方程 课件(共19张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 17.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-03 16:05:18 | ||
图片预览






文档简介
(共19张PPT)
椭圆及其标准方程
目录
一、椭圆的定义
二、椭圆的标准方程
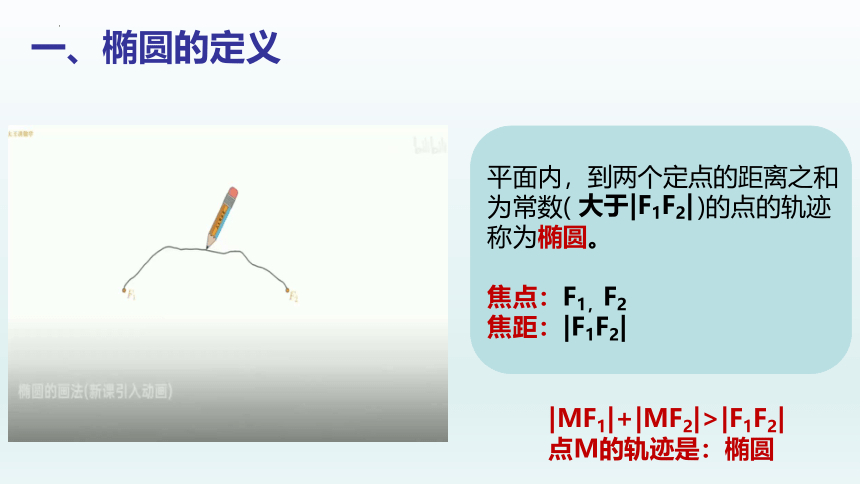
一、椭圆的定义
平面内,到两个定点的距离之和为常数( )的点的轨迹称为椭圆。
|MF1|+|MF2|>|F1F2|
点M的轨迹是:椭圆
大于|F1F2|
焦点:F1,F2
焦距:|F1F2|
二、快问快答
判断题
1、平面内,点到两定点的距离之和为常数的点的轨迹,是椭圆。( )
×
|MF1|+|MF2|=|F1F2|
点M的轨迹是:线段F1F2
判断题
2、平面内,到两定点的距离之和小于|F1F2|的点的轨迹,是椭圆。( )
×
|MF1|+|MF2|<|F1F2|
点M的轨迹是:无轨迹
平面内,到两个定点F1, F2的距离之和为常数 的点M的轨迹称为 。
情况一:当|MF1|+|MF2|>|F1F2|,点M的轨迹是:椭圆
情况二:当|MF1|+|MF2|=|F1F2|,点M的轨迹是:线段F1F2
情况三:当|MF1|+|MF2|<|F1F2|,点M的轨迹不存在
1、建系
三、推导椭圆的标准方程1
2、设点
3、列式
4、化简
求圆的标准方程的步骤:
(一)小组探讨,建系方案
提示:尽可能使方程的运算简单(一般利用对称性)
F1
F2
O
y
x
F1
F2
y
O
O
x
方案一:焦点在x轴上
方案二:焦点在y轴上
以焦点所在直线为 x 轴,线段F1F2的垂直平分线为 y 轴,建立直角坐标系。
1、建系
(二)推导椭圆的标准方程1
2、设点
3、列式
令焦距为2c,
则|F1F2|=2c
任取椭圆上一点M,设M (x,y)
|MF1|+|MF2|=2a
∴
M (x,y)
(-c,0)
(c,0)
|MF1|+|MF2|=定长。
∵ O点是线段F1F2的中点
∴ |OF1|=|OF2|=c
(a>c>0)
设定长为2a
两边同时平方:
化简得:
\
\
化简尝试一:两边同时平方
化简尝试二:移项后再平方
移项 :
4、化简
(三)小组PK
(a -c )x +a y =a (a -c )
∵ a>c>0
该方程表示:焦点在x轴上的椭圆。
∴ b x +a y =a b
∵ a>0,b>0
∴ 等式的左右两边同时除以a b
(四)椭圆的标准方程:
(a>b>0)
(-c,0)
(c,0)
∴ a -c >0,令a -c =b (b>0)
三、推导椭圆的标准方程2
椭圆的标准方程:
(a>b>0)
该方程表示:焦点在y轴上的椭圆。
四、例题讲解
求椭圆的标准方程.
(1)焦点在x轴上,焦距为6,椭圆上的点到两个焦点的距离之和为10.
解:
∵ 焦点在x轴上
∴ 设:椭圆的标准方程是:
已知: 2c=6,c=3
由题意得:2a=10,a=5
∴ a =25
(a>b>0)
∵ a =b +c
∴ 25=b +9
∴ b =16
代入a ,b
∴
答:椭圆的标准方程是:
五、课堂练习
求椭圆的标准方程.
(1)a=4,b=1,焦点在x轴上. (2)b=,c=5,焦点在y轴上.
解:
∵ 焦点在x轴上
∴ 设:椭圆的标准方程是:
已知: a=4,b=1
∴ a =16,b =1
代入a ,b
椭圆的标准方程是:
(a>b>0)
解:
∵ 焦点在y轴上
∴ 设:椭圆的标准方程是:
∵ b=,c=5
∴ b =10
∵ a =b +c =10+25=35
代入a ,b
椭圆的标准方程是:
(a>b>0)
椭圆定义
椭圆图象
y
F1
F2
O
x
y
x
F1
F2
O
|MF1|+|MF2|>|F1F2|
焦点
a、b、c
F1 (-c,0),F2 (c,0)
F1 (0,-c),F2 (0,c)
标准方程
(a>b>0)
(a>b>0)
|MF1|+|MF2|=2a;
a =b +c .
焦距:2c;
六、课堂小结
七、课后作业
1、如果椭圆上一点P与焦点F1的距离等于6,那么点P与另一个焦点F2的距离是 .
2、求适合下列条件的椭圆的标准方程:
(1)a=4,b=2,焦点在x轴上. (2)a=,c=,焦点在y轴上.
(3)a+b=10,c=2.
七、课后作业
4、已知A,B两点的坐标分别是(-1,0),(1,0),直线AM,BM相交于点M,且直线AM的斜率与直线BM的斜率的商是2,点M的轨迹是什么?为什么?
3、经过椭圆的右焦点F2作垂直于x轴的直线AB,交椭圆于A,B两点,F1是椭圆的左焦点。
(1)求▲AF1B的周长。
(2)如果AB不垂直于x轴,▲AF1B的周长有变化吗?为什么?
谢谢观看
椭圆及其标准方程
目录
一、椭圆的定义
二、椭圆的标准方程
一、椭圆的定义
平面内,到两个定点的距离之和为常数( )的点的轨迹称为椭圆。
|MF1|+|MF2|>|F1F2|
点M的轨迹是:椭圆
大于|F1F2|
焦点:F1,F2
焦距:|F1F2|
二、快问快答
判断题
1、平面内,点到两定点的距离之和为常数的点的轨迹,是椭圆。( )
×
|MF1|+|MF2|=|F1F2|
点M的轨迹是:线段F1F2
判断题
2、平面内,到两定点的距离之和小于|F1F2|的点的轨迹,是椭圆。( )
×
|MF1|+|MF2|<|F1F2|
点M的轨迹是:无轨迹
平面内,到两个定点F1, F2的距离之和为常数 的点M的轨迹称为 。
情况一:当|MF1|+|MF2|>|F1F2|,点M的轨迹是:椭圆
情况二:当|MF1|+|MF2|=|F1F2|,点M的轨迹是:线段F1F2
情况三:当|MF1|+|MF2|<|F1F2|,点M的轨迹不存在
1、建系
三、推导椭圆的标准方程1
2、设点
3、列式
4、化简
求圆的标准方程的步骤:
(一)小组探讨,建系方案
提示:尽可能使方程的运算简单(一般利用对称性)
F1
F2
O
y
x
F1
F2
y
O
O
x
方案一:焦点在x轴上
方案二:焦点在y轴上
以焦点所在直线为 x 轴,线段F1F2的垂直平分线为 y 轴,建立直角坐标系。
1、建系
(二)推导椭圆的标准方程1
2、设点
3、列式
令焦距为2c,
则|F1F2|=2c
任取椭圆上一点M,设M (x,y)
|MF1|+|MF2|=2a
∴
M (x,y)
(-c,0)
(c,0)
|MF1|+|MF2|=定长。
∵ O点是线段F1F2的中点
∴ |OF1|=|OF2|=c
(a>c>0)
设定长为2a
两边同时平方:
化简得:
\
\
化简尝试一:两边同时平方
化简尝试二:移项后再平方
移项 :
4、化简
(三)小组PK
(a -c )x +a y =a (a -c )
∵ a>c>0
该方程表示:焦点在x轴上的椭圆。
∴ b x +a y =a b
∵ a>0,b>0
∴ 等式的左右两边同时除以a b
(四)椭圆的标准方程:
(a>b>0)
(-c,0)
(c,0)
∴ a -c >0,令a -c =b (b>0)
三、推导椭圆的标准方程2
椭圆的标准方程:
(a>b>0)
该方程表示:焦点在y轴上的椭圆。
四、例题讲解
求椭圆的标准方程.
(1)焦点在x轴上,焦距为6,椭圆上的点到两个焦点的距离之和为10.
解:
∵ 焦点在x轴上
∴ 设:椭圆的标准方程是:
已知: 2c=6,c=3
由题意得:2a=10,a=5
∴ a =25
(a>b>0)
∵ a =b +c
∴ 25=b +9
∴ b =16
代入a ,b
∴
答:椭圆的标准方程是:
五、课堂练习
求椭圆的标准方程.
(1)a=4,b=1,焦点在x轴上. (2)b=,c=5,焦点在y轴上.
解:
∵ 焦点在x轴上
∴ 设:椭圆的标准方程是:
已知: a=4,b=1
∴ a =16,b =1
代入a ,b
椭圆的标准方程是:
(a>b>0)
解:
∵ 焦点在y轴上
∴ 设:椭圆的标准方程是:
∵ b=,c=5
∴ b =10
∵ a =b +c =10+25=35
代入a ,b
椭圆的标准方程是:
(a>b>0)
椭圆定义
椭圆图象
y
F1
F2
O
x
y
x
F1
F2
O
|MF1|+|MF2|>|F1F2|
焦点
a、b、c
F1 (-c,0),F2 (c,0)
F1 (0,-c),F2 (0,c)
标准方程
(a>b>0)
(a>b>0)
|MF1|+|MF2|=2a;
a =b +c .
焦距:2c;
六、课堂小结
七、课后作业
1、如果椭圆上一点P与焦点F1的距离等于6,那么点P与另一个焦点F2的距离是 .
2、求适合下列条件的椭圆的标准方程:
(1)a=4,b=2,焦点在x轴上. (2)a=,c=,焦点在y轴上.
(3)a+b=10,c=2.
七、课后作业
4、已知A,B两点的坐标分别是(-1,0),(1,0),直线AM,BM相交于点M,且直线AM的斜率与直线BM的斜率的商是2,点M的轨迹是什么?为什么?
3、经过椭圆的右焦点F2作垂直于x轴的直线AB,交椭圆于A,B两点,F1是椭圆的左焦点。
(1)求▲AF1B的周长。
(2)如果AB不垂直于x轴,▲AF1B的周长有变化吗?为什么?
谢谢观看
