完全平方公式[上学期]
图片预览




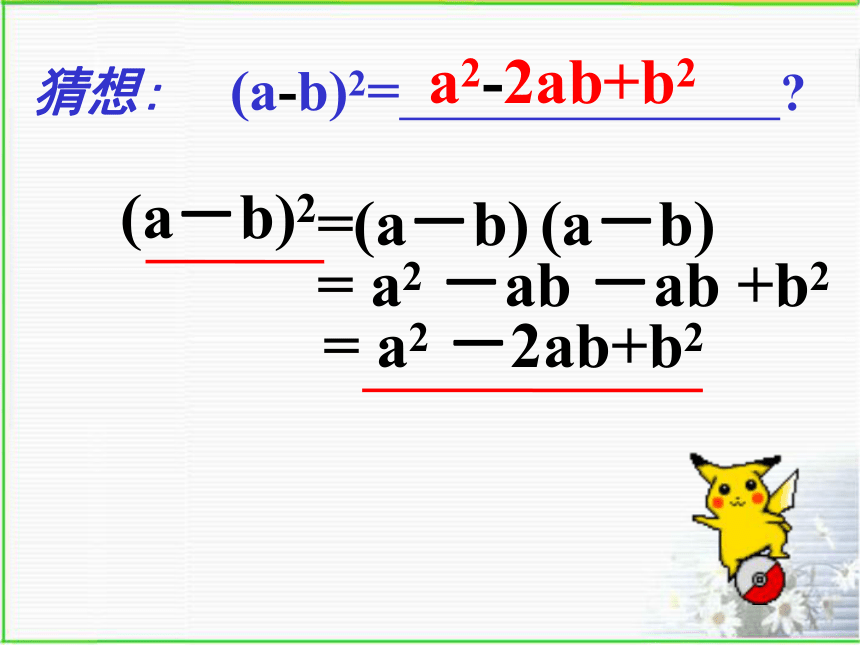



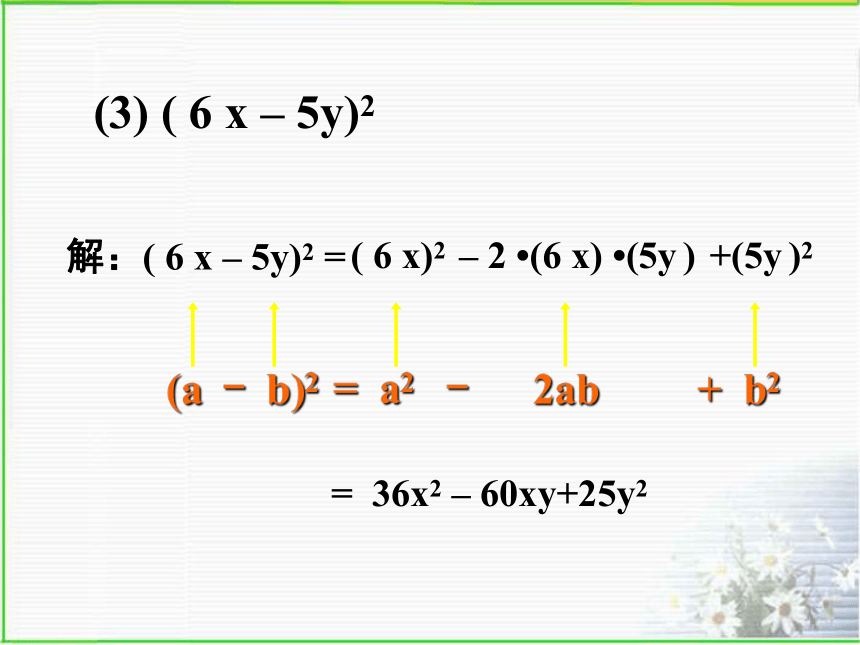

文档简介
课件30张PPT。15.3.2 完全平方公式 多项式乘法公式:1.(a+b)(c+d) =
平方差公式:(a+b)(a-b) = a2-b2ac+ad+bc+bd2.(x+a)(x+b) =x2+(a+b)x+ab复习判断下列计算是否正确:√√ 一块边长为a米的正方形实验田, 因需要将其边长增加 b 米。形成四块
实验田,以种植不同的新品种
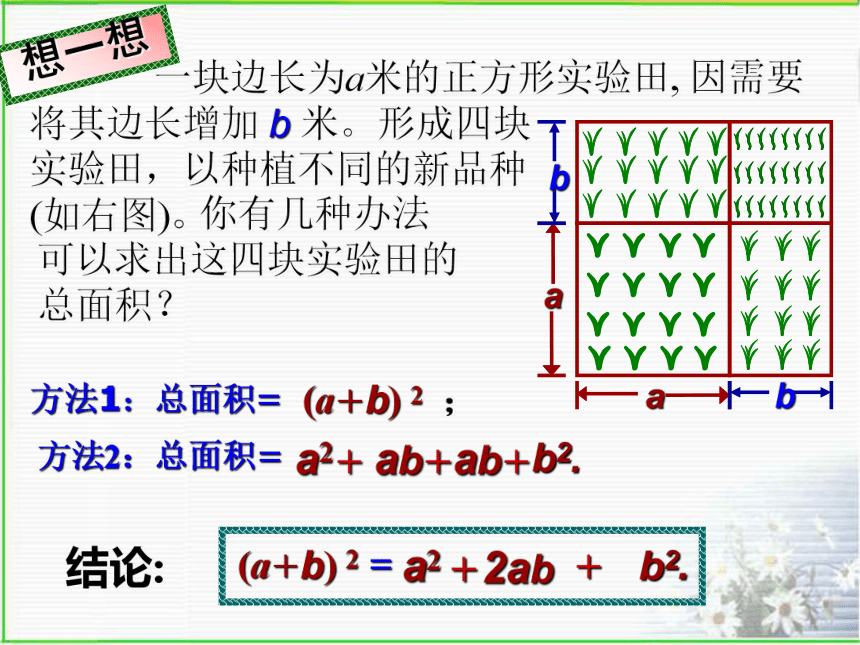
(如右图)。方法1:总面积= 你有几种办法可以求出这四块实验田的总面积?(a+b) 2 ;方法2:总面积=结论:=(a+b) 2想一想探
究 =(a+b)(a+b)
=a2+ab+ba+ b2
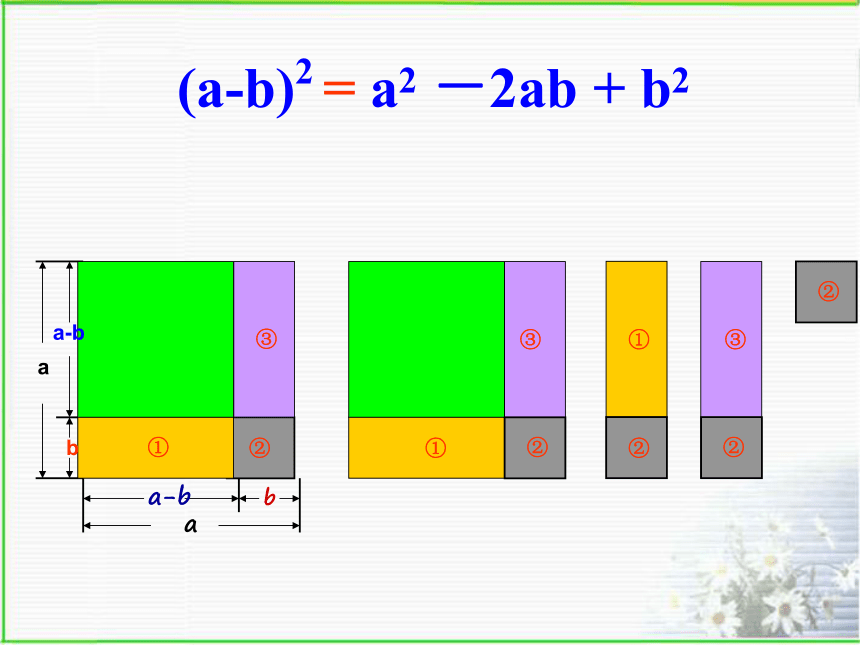
=a2+2ab+b2 (a+b)2(a+b)2=a2+2ab+b2(a-b)2= a2 -2ab+b2= a2 -ab -ab +b2=(a-b) (a-b)猜想: (a-b)2= ?a2-2ab+b2a-bbaa-bb a①②③③②①②②②①(a-b)2 = a2 -2ab + b2
③(a+b)2 = a2 + 2ab + b2(a-b)2 = a2 - 2ab + b2
两数和 的平方,等于两数的平方和,
加上 它们的积的两倍.( 差)(减去)完全平方公式:公式特点:4、公式中的字母a,b可以表示数,单项式和
多项式。(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b21、积为二次三项式;2、积中两项为两数的平方和;3、另一项是两数积的2倍,且与乘式中
间的符号相同。首平方,尾平方,首尾两倍中间放,加的加减的减.谐音记忆:例题1=(2y)2=(3m)2+52+(n)2-2·(3m)·(n)运用完全平方公式计算:= 4y2 +20y+25= 9m2 -6mn+ n2小结:运用完全平方公式的关键是找准公式中a和b= 36x2 – 60xy+25y2+(5y )2解:( 6 x – 5y)2 =(a - b)2 = a2 - 2ab + b2 ( 6 x)2– 2 ?(6 x) ?(5y )(3) ( 6 x – 5y)2(2) (a - b)2 与 (b - a)2 、
(-b +a)2 与(-a +b)2(1) (-a -b)2 与(a+b)2比较下列各式之间的关系:相等相等= +2(2m)·3n解:(-a-b)2 =(a+b)2也可以这样计算:=(-3a)2= 9a2 + 12ab + 4b2+(-2b)2-2·(-3a)·2b= [-(3a+2b)]2= (3a+2b)2= (3a)2= 9a2 + 12ab + 4b2+(2b)2+2·(3a)·2b1.(-x-y)2= 2.(-2a2+b)2= 你会了吗?(x+ y)2=x2+2xxy+y2(2a2-b)2=4a4-4a2b+b2
(1)(a+b)2=a2+b2 ( )
(2)(7-a)2=49-14a+a2 ( )
(3)(a+2b)2=a2+2ab+b2 ( )
(4)(a-2b)2=a2-4ab-4b2 ( ) 判断正误:×××√填空:-2x4-4ab综合尝试,实践应用-2ab 运用完全平方公式计算:
(4a-b)2 2) (y+ )2
3)(-2x-1)2 4) (b2+4a2)221解:1) (4a-b)2练一练=y2= (4a)2
= 16a2-8ab+b2-2·4a·b+b2+2· y · 3) (-2x-1)2原式 =[-(2x+1)]2 =(2x+1)2
=(2x)2+2·2x·1+1=4x2+4x+1一二一三二三4) (b2+4a2)2解:原式 = (b2)2+2· b2 · (4a2) + (4a2)2
= b4 +8 a2 b2 + 16a4 (1) (6a+5b)2
=36a2+60ab+25b2 (2) (4x-3y)2
=16x2-24xy+9y2 (3) (2m-1)2
=4m2-4m+1 (3) (-2m-1)2
=4m2+4m+1再练例2.运用完全平方公式计算:
1) 1022 2) 1992解:1) 1022 = (100+2)2
= 1002+2×100×2+22
= 10000+400+4
= 10404
2)1992 = (200-1)2
=2002-2×200×1+12
= 40000-400+1
= 39601(A) (p+q)2=p2+q2(B) (a+2b)2=a2+4ab+2b2(C) (a2+1)2=a4+2a+1(D) (-s+t)2=s2-2st+t2 下列计算中正确的是( )D选一选选一选:
(mn+3)2= ,
mn2+9 (B) m2n2+9
(C) m2n2+6mn+9 (D) mn2+6m+9cwww.czsx.com.cn思考题(2)计算[ (a+b)+c)]2=?原式=(a+b)2+2(a+b)c+c2 = a2+2ab+b2+2ac+2bc+c2 = a2+b2+c2+2ab+2ac+2bc例4:运用乘法公式计算
(1)(x+2y-3)(x-2y+3)
(2)(2x-y-z)2
(3)(3x-4y)2(3x+4y)2
例5:化简并求值
2(x+2)2-(x+2)(x-2)-(x+3)(1-x)
其中 x=-1例6:已知x+y=5,xy=6,求
(1)x2+y2 (2)x-y的值
练习拓展:
已知 x + =3,求x2+ 的值再见
平方差公式:(a+b)(a-b) = a2-b2ac+ad+bc+bd2.(x+a)(x+b) =x2+(a+b)x+ab复习判断下列计算是否正确:√√ 一块边长为a米的正方形实验田, 因需要将其边长增加 b 米。形成四块
实验田,以种植不同的新品种
(如右图)。方法1:总面积= 你有几种办法可以求出这四块实验田的总面积?(a+b) 2 ;方法2:总面积=结论:=(a+b) 2想一想探
究 =(a+b)(a+b)
=a2+ab+ba+ b2
=a2+2ab+b2 (a+b)2(a+b)2=a2+2ab+b2(a-b)2= a2 -2ab+b2= a2 -ab -ab +b2=(a-b) (a-b)猜想: (a-b)2= ?a2-2ab+b2a-bbaa-bb a①②③③②①②②②①(a-b)2 = a2 -2ab + b2
③(a+b)2 = a2 + 2ab + b2(a-b)2 = a2 - 2ab + b2
两数和 的平方,等于两数的平方和,
加上 它们的积的两倍.( 差)(减去)完全平方公式:公式特点:4、公式中的字母a,b可以表示数,单项式和
多项式。(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b21、积为二次三项式;2、积中两项为两数的平方和;3、另一项是两数积的2倍,且与乘式中
间的符号相同。首平方,尾平方,首尾两倍中间放,加的加减的减.谐音记忆:例题1=(2y)2=(3m)2+52+(n)2-2·(3m)·(n)运用完全平方公式计算:= 4y2 +20y+25= 9m2 -6mn+ n2小结:运用完全平方公式的关键是找准公式中a和b= 36x2 – 60xy+25y2+(5y )2解:( 6 x – 5y)2 =(a - b)2 = a2 - 2ab + b2 ( 6 x)2– 2 ?(6 x) ?(5y )(3) ( 6 x – 5y)2(2) (a - b)2 与 (b - a)2 、
(-b +a)2 与(-a +b)2(1) (-a -b)2 与(a+b)2比较下列各式之间的关系:相等相等= +2(2m)·3n解:(-a-b)2 =(a+b)2也可以这样计算:=(-3a)2= 9a2 + 12ab + 4b2+(-2b)2-2·(-3a)·2b= [-(3a+2b)]2= (3a+2b)2= (3a)2= 9a2 + 12ab + 4b2+(2b)2+2·(3a)·2b1.(-x-y)2= 2.(-2a2+b)2= 你会了吗?(x+ y)2=x2+2xxy+y2(2a2-b)2=4a4-4a2b+b2
(1)(a+b)2=a2+b2 ( )
(2)(7-a)2=49-14a+a2 ( )
(3)(a+2b)2=a2+2ab+b2 ( )
(4)(a-2b)2=a2-4ab-4b2 ( ) 判断正误:×××√填空:-2x4-4ab综合尝试,实践应用-2ab 运用完全平方公式计算:
(4a-b)2 2) (y+ )2
3)(-2x-1)2 4) (b2+4a2)221解:1) (4a-b)2练一练=y2= (4a)2
= 16a2-8ab+b2-2·4a·b+b2+2· y · 3) (-2x-1)2原式 =[-(2x+1)]2 =(2x+1)2
=(2x)2+2·2x·1+1=4x2+4x+1一二一三二三4) (b2+4a2)2解:原式 = (b2)2+2· b2 · (4a2) + (4a2)2
= b4 +8 a2 b2 + 16a4 (1) (6a+5b)2
=36a2+60ab+25b2 (2) (4x-3y)2
=16x2-24xy+9y2 (3) (2m-1)2
=4m2-4m+1 (3) (-2m-1)2
=4m2+4m+1再练例2.运用完全平方公式计算:
1) 1022 2) 1992解:1) 1022 = (100+2)2
= 1002+2×100×2+22
= 10000+400+4
= 10404
2)1992 = (200-1)2
=2002-2×200×1+12
= 40000-400+1
= 39601(A) (p+q)2=p2+q2(B) (a+2b)2=a2+4ab+2b2(C) (a2+1)2=a4+2a+1(D) (-s+t)2=s2-2st+t2 下列计算中正确的是( )D选一选选一选:
(mn+3)2= ,
mn2+9 (B) m2n2+9
(C) m2n2+6mn+9 (D) mn2+6m+9cwww.czsx.com.cn思考题(2)计算[ (a+b)+c)]2=?原式=(a+b)2+2(a+b)c+c2 = a2+2ab+b2+2ac+2bc+c2 = a2+b2+c2+2ab+2ac+2bc例4:运用乘法公式计算
(1)(x+2y-3)(x-2y+3)
(2)(2x-y-z)2
(3)(3x-4y)2(3x+4y)2
例5:化简并求值
2(x+2)2-(x+2)(x-2)-(x+3)(1-x)
其中 x=-1例6:已知x+y=5,xy=6,求
(1)x2+y2 (2)x-y的值
练习拓展:
已知 x + =3,求x2+ 的值再见
