2.4线段的垂直平分线(第2课时) 课件(共18张PPT) 青岛版数学八年级上册
文档属性
| 名称 | 2.4线段的垂直平分线(第2课时) 课件(共18张PPT) 青岛版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 565.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-04 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
2.4 线段的垂直平分线(第2课时)
线段垂直平分线上的点到线段两端的距离相等.
2.线段垂直平分线的性质
到线段两端距离相等的点在线段的垂直平分线上.
温故知新
3.线段垂直平分线的判定
1.线段垂直平分线的定义
垂直并且平分一条线段的直线叫做这条线段的垂直平分线.
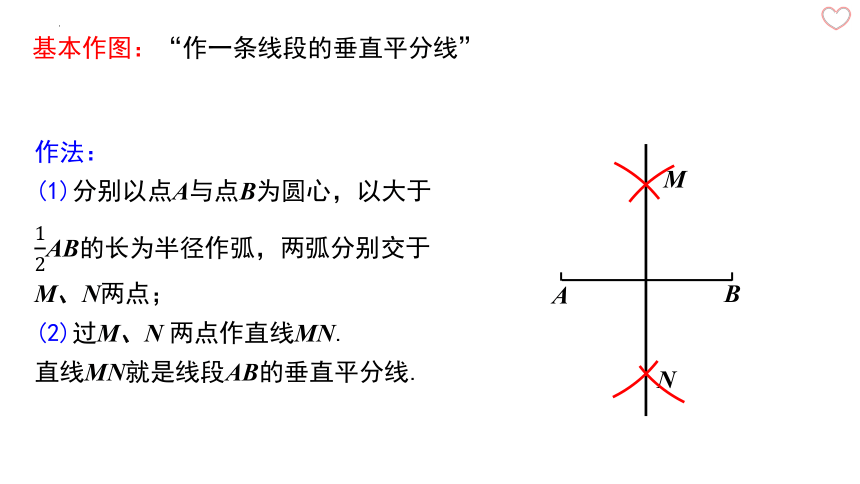
基本作图:“作一条线段的垂直平分线”
作法:
(1)分别以点A与点B为圆心,以大于AB的长为半径作弧,两弧分别交于M、N两点;
(2)过M、N 两点作直线MN.
直线MN就是线段AB的垂直平分线.
A
B
M
N
已知三个村庄的位置如图所示,经过商量,三个村庄决定联合打一眼机井向三个村庄供水,要想使机井到三个村庄的距离相等,机井应该设在何处?并说明你的理由.
实验与探究
A
B
C
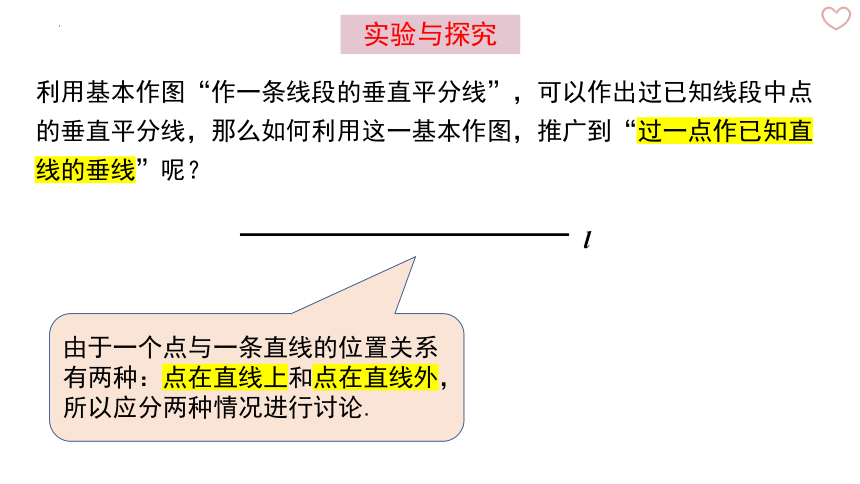
利用基本作图“作一条线段的垂直平分线”,可以作出过已知线段中点的垂直平分线,那么如何利用这一基本作图,推广到“过一点作已知直线的垂线”呢?
l
由于一个点与一条直线的位置关系有两种:点在直线上和点在直线外,所以应分两种情况进行讨论.
实验与探究
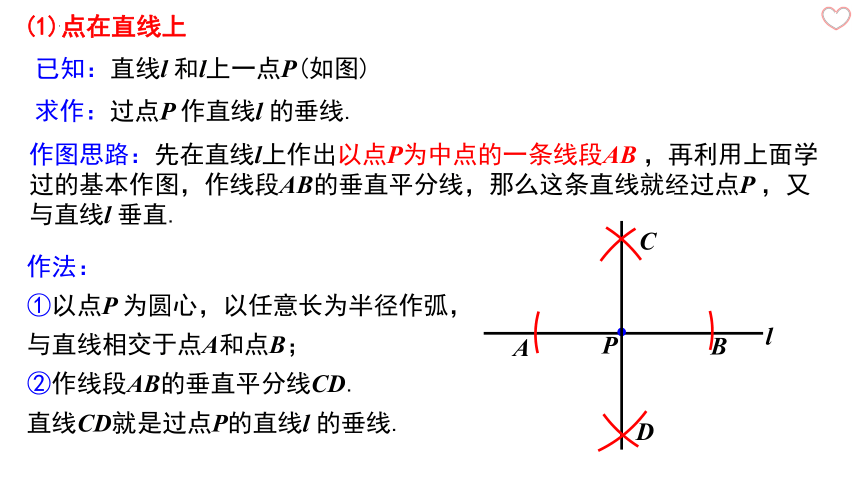
(1)点在直线上
求作:过点P 作直线l 的垂线.
已知:直线l 和l上一点P(如图)
作图思路:先在直线l上作出以点P为中点的一条线段AB ,再利用上面学过的基本作图,作线段AB的垂直平分线,那么这条直线就经过点P ,又与直线l 垂直.
作法:
①以点P 为圆心,以任意长为半径作弧,与直线相交于点A和点B;
②作线段AB的垂直平分线CD.
直线CD就是过点P的直线l 的垂线.
P
A
B
C
D
l
(2)点在直线外
求作:过点P 作直线l 的垂线.
已知:直线l 和l 外一点P(如图)
P
作图思路:
先在直线l上作出一条线段AB ,并且使点P到线段AB两端的距离相等,
再利用基本作图“作线段AB的垂直平分线”,那么这条直线经过点P ,又与直线l垂直.
l
P
K
作法:
①任意取一点K,使点K和点P分别在直线l 的两侧;
②以点P为圆心, PK的长为半径作弧,与直线l相交于点A和点B;
③作线段AB的垂直平分线CD.
直线CD就是过点P的直线l 的垂线.
A
B
C
D
l
最短路径问题
A
l
P
依据:垂线段最短
类型一:一个点
(在l上找一点P,使PA最短)
类型二:两点异侧
(在l上找一点P,使PA+ PB最短)
A
l
B
P
依据:两点之间线段最短
点P 即为所求作的点.
点P 即为所求作的点.
类型三:两点同侧(在l上找一点P,使PA+ PB最短)
A
l
B
C
B′
P
依据:两点之间线段最短
点P 即为所求作的点.
A
l
B
将本题抽象为数学语言:
已知点A ,B两点在直线l的同侧,在直线l上求作一点P,使AP+BP的值最小.
例题鉴赏
例1 海伦是古希腊的一位数学家,测量学家.相传,有一天一位将军专程拜访海伦,求教一个令他百思不得其解的问题:“我每天策马往返于两个边防站A与B之间,途中都要到小河l 边让马饮水.怎样走路程最近呢?”你能帮将军解答这个问题吗?说出你的作法,在图中作出最近的路线.
作法:
(1)过点B作直线l 的垂线BC,垂足为C;
(2)在BC上截取点B′,使B,B′分别在l 的两侧,且CB′ = CB;
(3)连接AB′,与直线l交于点P;
点P就是所求作的直线l 使AP+BP的值最小的点
A
l
B
C
B′
P
B
A
C
D
在AC上找一点P,使PB+ PD最短
D′
P
B
A
C
D
在AC上找一点P,使PB+ PD最短
B′
P
类型四:角内两点 (在l1、 l2上找点P、Q,使路径最短)
B
A
l1
l2
A′
B′
P
Q
类型五:角内一点 (在OA上找点E 、 OB上找点F,使△PEF的周长最短)
B
A
O
P
P1
P2
E
F
请你说明作图的道理
理由:因为点B,B′ 关于直线l 对称,根据轴对称的基本性质, l 是BB′ 的垂直平分线,所以PB=PB′ .
如果再在直线l上另取一点P′ ,
连接AP′ , B′ P′ ,
根据三角形的三边关系的性质(或两点之间线段最短)可知:
AP′ + B′ P′ >AB′,
即AP′ + B′ P′ > AP+BP,
所以AP + BP 的值最小,
将军走的路程最近。
A
l
B
C
B′
P
P′
作 业
中午作业:
作业:
《同步练习册》
《同步练习册》
2.4 线段的垂直平分线(第2课时)
线段垂直平分线上的点到线段两端的距离相等.
2.线段垂直平分线的性质
到线段两端距离相等的点在线段的垂直平分线上.
温故知新
3.线段垂直平分线的判定
1.线段垂直平分线的定义
垂直并且平分一条线段的直线叫做这条线段的垂直平分线.
基本作图:“作一条线段的垂直平分线”
作法:
(1)分别以点A与点B为圆心,以大于AB的长为半径作弧,两弧分别交于M、N两点;
(2)过M、N 两点作直线MN.
直线MN就是线段AB的垂直平分线.
A
B
M
N
已知三个村庄的位置如图所示,经过商量,三个村庄决定联合打一眼机井向三个村庄供水,要想使机井到三个村庄的距离相等,机井应该设在何处?并说明你的理由.
实验与探究
A
B
C
利用基本作图“作一条线段的垂直平分线”,可以作出过已知线段中点的垂直平分线,那么如何利用这一基本作图,推广到“过一点作已知直线的垂线”呢?
l
由于一个点与一条直线的位置关系有两种:点在直线上和点在直线外,所以应分两种情况进行讨论.
实验与探究
(1)点在直线上
求作:过点P 作直线l 的垂线.
已知:直线l 和l上一点P(如图)
作图思路:先在直线l上作出以点P为中点的一条线段AB ,再利用上面学过的基本作图,作线段AB的垂直平分线,那么这条直线就经过点P ,又与直线l 垂直.
作法:
①以点P 为圆心,以任意长为半径作弧,与直线相交于点A和点B;
②作线段AB的垂直平分线CD.
直线CD就是过点P的直线l 的垂线.
P
A
B
C
D
l
(2)点在直线外
求作:过点P 作直线l 的垂线.
已知:直线l 和l 外一点P(如图)
P
作图思路:
先在直线l上作出一条线段AB ,并且使点P到线段AB两端的距离相等,
再利用基本作图“作线段AB的垂直平分线”,那么这条直线经过点P ,又与直线l垂直.
l
P
K
作法:
①任意取一点K,使点K和点P分别在直线l 的两侧;
②以点P为圆心, PK的长为半径作弧,与直线l相交于点A和点B;
③作线段AB的垂直平分线CD.
直线CD就是过点P的直线l 的垂线.
A
B
C
D
l
最短路径问题
A
l
P
依据:垂线段最短
类型一:一个点
(在l上找一点P,使PA最短)
类型二:两点异侧
(在l上找一点P,使PA+ PB最短)
A
l
B
P
依据:两点之间线段最短
点P 即为所求作的点.
点P 即为所求作的点.
类型三:两点同侧(在l上找一点P,使PA+ PB最短)
A
l
B
C
B′
P
依据:两点之间线段最短
点P 即为所求作的点.
A
l
B
将本题抽象为数学语言:
已知点A ,B两点在直线l的同侧,在直线l上求作一点P,使AP+BP的值最小.
例题鉴赏
例1 海伦是古希腊的一位数学家,测量学家.相传,有一天一位将军专程拜访海伦,求教一个令他百思不得其解的问题:“我每天策马往返于两个边防站A与B之间,途中都要到小河l 边让马饮水.怎样走路程最近呢?”你能帮将军解答这个问题吗?说出你的作法,在图中作出最近的路线.
作法:
(1)过点B作直线l 的垂线BC,垂足为C;
(2)在BC上截取点B′,使B,B′分别在l 的两侧,且CB′ = CB;
(3)连接AB′,与直线l交于点P;
点P就是所求作的直线l 使AP+BP的值最小的点
A
l
B
C
B′
P
B
A
C
D
在AC上找一点P,使PB+ PD最短
D′
P
B
A
C
D
在AC上找一点P,使PB+ PD最短
B′
P
类型四:角内两点 (在l1、 l2上找点P、Q,使路径最短)
B
A
l1
l2
A′
B′
P
Q
类型五:角内一点 (在OA上找点E 、 OB上找点F,使△PEF的周长最短)
B
A
O
P
P1
P2
E
F
请你说明作图的道理
理由:因为点B,B′ 关于直线l 对称,根据轴对称的基本性质, l 是BB′ 的垂直平分线,所以PB=PB′ .
如果再在直线l上另取一点P′ ,
连接AP′ , B′ P′ ,
根据三角形的三边关系的性质(或两点之间线段最短)可知:
AP′ + B′ P′ >AB′,
即AP′ + B′ P′ > AP+BP,
所以AP + BP 的值最小,
将军走的路程最近。
A
l
B
C
B′
P
P′
作 业
中午作业:
作业:
《同步练习册》
《同步练习册》
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
