27.2.2 相似三角形的性质 课件(共16张PPT) 人教版九年级数学下册
文档属性
| 名称 | 27.2.2 相似三角形的性质 课件(共16张PPT) 人教版九年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-04 11:27:06 | ||
图片预览




文档简介
(共16张PPT)
第二十七章 相似
27.2.2
相似三角形的性质
知识回顾
1.三角形相似的判定方法:
(1)定义法:三个对应角相等,三条对应边成比例的两个三角形相似。
(2)平行法:平行于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的三角形与原三角形相似;
(3)判定定理1(边边边):三边对应成比例,两三角形相似;
(4)判定定理2(边角边):两边对应成比例且夹角相等,两三角形相似;
(5)判定定理3(角角):两角对应相等,两三角形相似;
(6)直角三角形相似的判定定理(HL):斜边和一条直角边成比例的两个直角三角形相似。
知识回顾
2.相似三角形的性质:
(1)相似三角形对应角相等、对应边成比例。
(2)相似三角形对应边上的高线之比、对应边上中线之比、对应角平分线之比等于相似比. 相似三角形对应线段之比等于相似比。
(3)相似三角形的周长之比等于相似比。
(4)相似三角形的面积之比等于相似比的平方。
如果两个三角形相似,它们对应的高、中线、角平分线、周长之间有什么关系?两个相似多边形呢?
探究思考
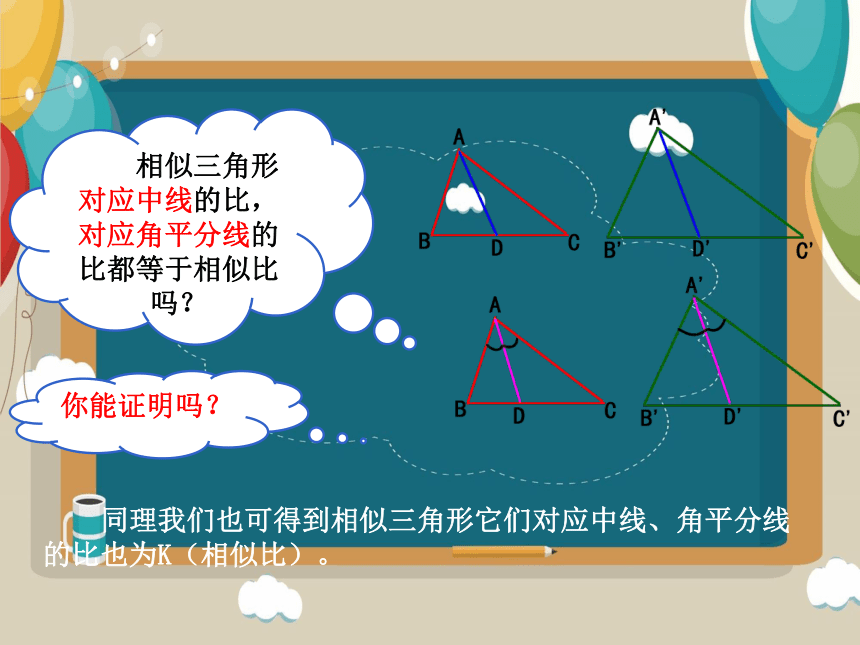
相似三角形对应中线的比,对应角平分线的比都等于相似比吗?
你能证明吗?
同理我们也可得到相似三角形它们对应中线、角平分线的比也为K(相似比)。
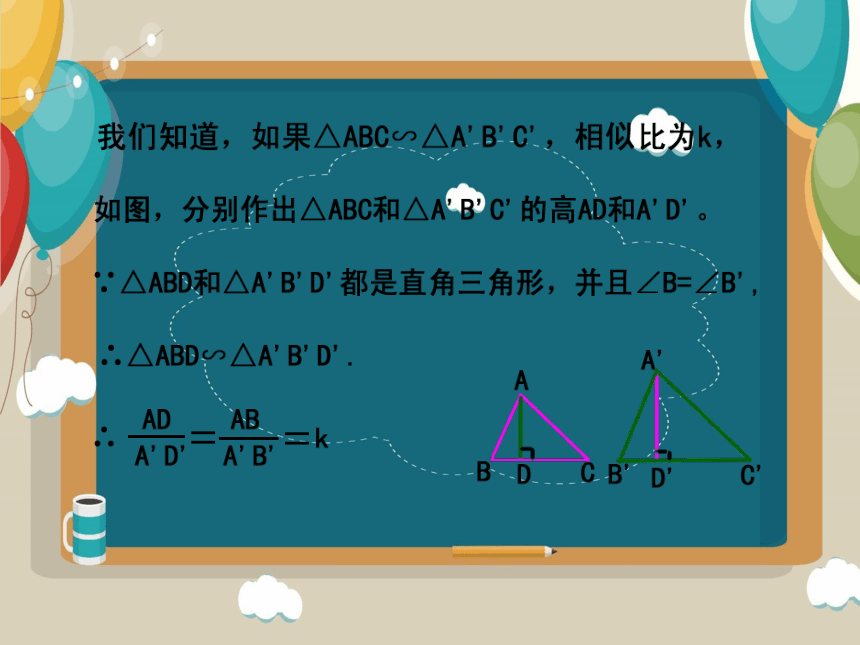
相似三角形对应高的比,对应中线的比,对应角平分线的比都等于相似比。
相似三角形的周长的比等于相似比。
由此我们得到:
用类似的方法,还可以得出:
相似多边形周长的比等于相似比。
相似三角形对应线段的比等于相似比。
继续探究
K1
这样,我们得到:
相似三角形的面积比等于相似比的平方。
例3:如图,在△ABC和△DEF中,AB=2DE,AC=2DF, ∠A=∠D,△ABC的边BC上的高为6,面积是 ,求△DEF的边EF上的高和面积。
∵△ABC的边BC上的高为6,面积是
∴△DEF的边EF上的高为 ,
面积为
例题探究
练习:
已知:
∽△
△
,它们的周长分别
为144cm和120cm ,且BC=48cm,
1、
A
D
C
B
△
已知:如图,Rt
ABC,CD为斜边AB上的高,
求:
2、
3、三角形的一条中位线把三角形截成的一个小
三角形与原三角形的周长之比等于________,
面积之比等于________。
1:2
1:4
4、两个相似三角形对应的中线长分别是6cm和
18cm,若较大三角形的周长是42cm,面积是
,则较小三角形的周长为________cm,
面积为____ 。
14
4
5、已知:如图△ABC中,DE∥BC,AF⊥DE
垂足为F,AF交BC于G。若AF=5,FG=3,
则
A
F
E
D
B
C
G
H
N
M
F
E
D
C
B
A
6、如图在 ABCD中,E是BC的中点,是BE的中点,
AE与DF交于点H,过点H作MN⊥AD,垂足为M,
交BC于N,则NH:MH=______。
5
8
5
8
25
64
1:4
思考题:
A
B
D
C
E
在△ABC中,BC=m,DE∥BC,交AB于E,交AC于D, 求DE的长度。
这节课我们学习了相似三角形的另一重要性质:相似三角形周长的比等于相似比,相似三角形面积的比等于相似比的平方。
小结:
第二十七章 相似
27.2.2
相似三角形的性质
知识回顾
1.三角形相似的判定方法:
(1)定义法:三个对应角相等,三条对应边成比例的两个三角形相似。
(2)平行法:平行于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的三角形与原三角形相似;
(3)判定定理1(边边边):三边对应成比例,两三角形相似;
(4)判定定理2(边角边):两边对应成比例且夹角相等,两三角形相似;
(5)判定定理3(角角):两角对应相等,两三角形相似;
(6)直角三角形相似的判定定理(HL):斜边和一条直角边成比例的两个直角三角形相似。
知识回顾
2.相似三角形的性质:
(1)相似三角形对应角相等、对应边成比例。
(2)相似三角形对应边上的高线之比、对应边上中线之比、对应角平分线之比等于相似比. 相似三角形对应线段之比等于相似比。
(3)相似三角形的周长之比等于相似比。
(4)相似三角形的面积之比等于相似比的平方。
如果两个三角形相似,它们对应的高、中线、角平分线、周长之间有什么关系?两个相似多边形呢?
探究思考
相似三角形对应中线的比,对应角平分线的比都等于相似比吗?
你能证明吗?
同理我们也可得到相似三角形它们对应中线、角平分线的比也为K(相似比)。
相似三角形对应高的比,对应中线的比,对应角平分线的比都等于相似比。
相似三角形的周长的比等于相似比。
由此我们得到:
用类似的方法,还可以得出:
相似多边形周长的比等于相似比。
相似三角形对应线段的比等于相似比。
继续探究
K1
这样,我们得到:
相似三角形的面积比等于相似比的平方。
例3:如图,在△ABC和△DEF中,AB=2DE,AC=2DF, ∠A=∠D,△ABC的边BC上的高为6,面积是 ,求△DEF的边EF上的高和面积。
∵△ABC的边BC上的高为6,面积是
∴△DEF的边EF上的高为 ,
面积为
例题探究
练习:
已知:
∽△
△
,它们的周长分别
为144cm和120cm ,且BC=48cm,
1、
A
D
C
B
△
已知:如图,Rt
ABC,CD为斜边AB上的高,
求:
2、
3、三角形的一条中位线把三角形截成的一个小
三角形与原三角形的周长之比等于________,
面积之比等于________。
1:2
1:4
4、两个相似三角形对应的中线长分别是6cm和
18cm,若较大三角形的周长是42cm,面积是
,则较小三角形的周长为________cm,
面积为____ 。
14
4
5、已知:如图△ABC中,DE∥BC,AF⊥DE
垂足为F,AF交BC于G。若AF=5,FG=3,
则
A
F
E
D
B
C
G
H
N
M
F
E
D
C
B
A
6、如图在 ABCD中,E是BC的中点,是BE的中点,
AE与DF交于点H,过点H作MN⊥AD,垂足为M,
交BC于N,则NH:MH=______。
5
8
5
8
25
64
1:4
思考题:
A
B
D
C
E
在△ABC中,BC=m,DE∥BC,交AB于E,交AC于D, 求DE的长度。
这节课我们学习了相似三角形的另一重要性质:相似三角形周长的比等于相似比,相似三角形面积的比等于相似比的平方。
小结:
