3.7 探索与表达规律同步练习(含答案)
文档属性
| 名称 | 3.7 探索与表达规律同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 7.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-03 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第三章 整式及其加减
7 探索与表达规律
夯实基础逐点练
练点1 与图形有关的规律
1.一张长方形桌子需配6把椅子,按如图方式将桌子拼在一起,那么n张桌子需要配置的椅子把数为( )
A.2n+4 B.6+2n C.2n+8 D.6n
2.如图,用相同的圆点按照一定的规律拼出图形.第一幅图中有4个圆点,第二幅图中有7个圆点,第三幅图中有10个圆点,第四幅图中有13个圆点 按照此规律,第一百幅图中圆点的个数是( )
A.297 B.301 C.303 D.400
3.用正方形按如图所示的规律拼图案,其中第①个图案中有5个正方形,第②个图案中有9个正方形,第③个图案中有13个正方形,第④个图案中有17个正方形,按此规律排列下去,则第⑨个图案中正方形的个数为( )
A.32 B.34 C.37 D.41
练点2 与数或式有关的规律
4.观察下列数据: 则第 12个数是( )
5.有一列数:1,3,2,-1,…,其规律是从第二个数开始,每一个数都是其前后两个数之和,根据此规律,则第2024个数是( )
A.1 B.3 C.2 D.-1
练点3 与日历或数阵有关的规律
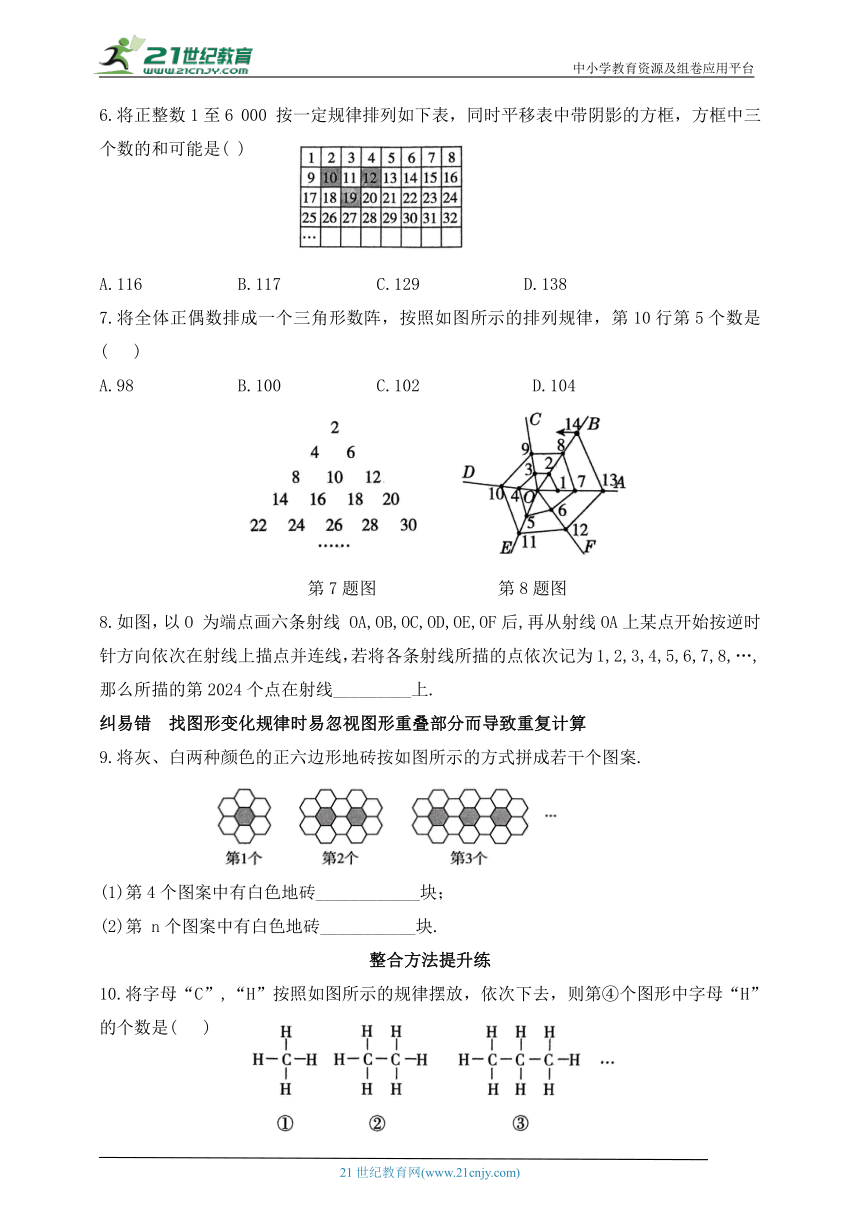
6.将正整数1至6 000 按一定规律排列如下表,同时平移表中带阴影的方框,方框中三个数的和可能是( )
A.116 B.117 C.129 D.138
7.将全体正偶数排成一个三角形数阵,按照如图所示的排列规律,第10行第5个数是( )
A.98 B.100 C.102 D.104
第7题图 第8题图
8.如图,以O 为端点画六条射线 OA,OB,OC,OD,OE,OF后,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为1,2,3,4,5,6,7,8,…,那么所描的第2024个点在射线_________上.
纠易错 找图形变化规律时易忽视图形重叠部分而导致重复计算
9.将灰、白两种颜色的正六边形地砖按如图所示的方式拼成若干个图案.
(1)第4个图案中有白色地砖____________块;
(2)第 n个图案中有白色地砖___________块.
整合方法提升练
10.将字母“C”,“H”按照如图所示的规律摆放,依次下去,则第④个图形中字母“H”的个数是( )
A.9 B.10 C.11 D.12
11.观察下列树枝分杈的规律图,若第 n个图中树枝数用 表示,则Y -Y =( )
A.15×2 B.31×2 C.33×2 D.63×2
12.观察下列等式:7°=1,7 =7,7 =49,7 =343,7 = 2401,7 =16807,…,根据其中的规律可得 7 的结果的个位数字是( )
A.0 B.1 C.7 D.8
13.下列图形是将等边三角形按一定规律排列,则第5个图形中所有等边三角形的个数是_____________.
14.将一列有理数 如图所示有序排列. 根据图中的排列规律可知,“峰1”中峰顶的位置(C的位置)是有理数4,那么“峰7”中C的位置是有理数_________,-103 应排在A,B,C,D,E中_____________的位置.
15.我们知道简便计算的好处,事实上,简便计算在好多地方都存在,观察下列等式:
15 =1×2×100 +25 =225,
25 =2×3×100 +25 =625,
35 =3×4×100+25 =1 225,
……
(1)根据上述等式反映出的规律填空:
95 =_______________=____________.
(2)设这类等式左边两位数的十位数字为a,请用一个含a的代数式表示其结果.
(3)这种简便计算也可以推广应用:个位数字是5的三位数的平方,请写出195 的简便计算过程及结果.
16.如图,正方形ABCD内部有若干个点,用这些点以及正方形 ABCD的顶点 A,B,C,D 把原正方形分割成一些三角形(互相不重叠).
(1)填写下表:
正方形ABCD内部点的个数 1 2 3 4 …
分割成的三角形的个数 4 6 …
(2)原正方形能否被分割成2 023个三角形 若能,求此时正方形 ABCD 内部有多少个点;若不能,请说明理由.
17.在如表所示2023年1月份日历中,用长方形的方框圈出任意3×3个数.
星期日 星期一 星期二 星期三 星期四 星期五 星期六
1 2 3 4 5 6 7
8 9 10 11 12 13 14
15 16 17 18 19 20 21
22 23 24 25 26 27 28
29 30 31
(1)如果从左下角到右上角的“对角线”上的3个数字的和为 36,那么这9个数的和为_____________.在这9个日期中,最后一天是___________号;
(2)在这个月的日历中,用方框能否圈出“总和为216”的9个数 如果能,请求出这9个日期正中间一天是几号;如果不能,请说明理由.
探究培优拓展练
18.式子 表示从1开始的连续 100个正整数的和,由于上述式子比较长,书写不方便,为了简便起见,可以将上述式子表示为 这里“∑”是求和的符号.例如 ’用“∑”可以表示为 用“∑”可以表示为
(1)把 写成加法的形式是____________;
用“∑”可以表示为_________;
(3)计算:
参考答案
1. A 【点拨】观察图形发现多一张桌子,则多2把椅子,所以n张桌子需要6+2(n-1)=2n+4(把)椅子.
2. B 【点拨】第一幅图中有4个圆点,4=4+3×0;第二幅图中有7个圆点,7=4+3=4+3×1;
第三幅图中有10个圆点,10=4+3+3=4+3×2;第四幅图中有13个圆点,13=4+3+3+3=4+3×3;…;那么第 n幅图中圆点的个数为4+3(n-1)=3n+1,所以第一百幅图中圆点的个数为 3×100+1=301.
3. C 【点拨】第①个图案中有5个正方形;
第②个图案中有9个正方形,9=5+4=5+4×1;
第③个图案中有13个正方形,13=5 +4+4=5+4×2;
第④个图案中有17个正方形,17=5+4+4+4=5+4×3;
…;
第n个图案中正方形的个数为5+4(n-1)=4n+1;
所以第⑨个图案中正方形的个数为4×9+1=37.
4. D【点拨】观察所给的数可知第 n个数是 所以第12个数是
5. B 【点拨】根据题意可知,这列数是1,3,2,-1,-3,-2,1,3,2,…,
发现1,3,2,-1,-3,-2,6个数一个循环,
因为 2 024÷6=337……2,所以第2024个数是3.
6. A 【点拨】设带阴影的方框中最小的数是x,则其他两个数是x+2,x+9,则x+x+2+x+9=3x+
11,令3x+11=116,则x=35;令3x+11=117,则 不是整数;令3x+11=129,则 不是整数;令3x+11=138,则 不是整数,所以和可能是116.
7. B【点拨】观察数字的变化可知,
第n行有n个偶数,
因为第1行的第1个数是2=1×0+2;
第2行的第1个数是4=2×1+2;
第3行的第1个数是8=3×2+2;…;
所以第n行的第1个数是 n(n-1)+2.
所以第10行第1个数是10×9+2=92,
所以第10行第5个数是92+2×4=100.
8. OB 【点拨】因为1在射线OA 上,2在射线OB上,3在射线OC上,4在射线OD上,5在射线OE上,6在射线OF上,7在射线OA上,…所以每6个数一个循环.
因为2024÷6=337 2,所以所描的第2024个点所在射线与2所在射线一样.
所以所描的第2024个点在射线OB上.
9.(1)18
(2)(4n+2)
【点拨】第1个图案中白色地砖的块数为4×1+2=6;
第2个图案中白色地砖的块数为4×2+2=10;
第3个图案中白色地砖的块数为4×3+2=14;
第4个图案中白色地砖的块数为4×4+2=18;
…;
第 n个图案中白色地砖的块数为 4n+2.
点易错 本题易错的原因是把第 n个图案当成由n个第1个图案组成,忽略了重叠部分.
10. B 【点拨】第①个图形中字母“H”的个数为4,
第②个图形中字母“H”的个数为4+2,
第③个图形中字母“H”的个数为4+2×2,
第④个图形中字母“H”的个数为4+2×3=10.
11. B 【点拨】由题图可得Y =1 =2 -1,Y =3=以此类推,可得 所以Y =2 -1,所以Y -Y =2 -1-2 +1 =31×2 .
12. B 【点拨】观察所给等式发现7"的个位数字按1,7,9,3 这4个数进行循环,
因为1+7+9+3=20,2 025÷4=506……1,所以 的结果的个位数字是1.
13.485 【点拨】第1个图形中有5个等边三角形,第2个图形中有5×3+2=17(个)等边三角形,第3个图形中有17×3+2=53(个)等边三角形,由此得出第4个图形中有53×3+2 =161(个)等边三角形,所以第5个图形中有161×3+2 =485(个)等边三角形.
14.34;B 【点拨】每五个数一个峰,且第奇数个峰中C的位置是正偶数,第偶数个峰中C的位置是负奇数,故“峰7”中C的位置是7×5-1=34.
因为(103-1)÷5=20……2,所以-103在B的位置.
15.【解】(1)9×10×100 +25;9 025
(2)(10a+5) =a·(a+1)×100 +25=100a(a+1)+25.
(3)195 =19×20×100+25=38 025.
16.【解】(1)8;10;2(n+1)
(2)不能.
设正方形ABCD内部有 a个点,则2(a+1)=2023,解得
因为 不是整数,所以原正方形不能被分割成2023个三角形.
17.【解】(1) 108;20 【点拨】设正中间的数是x,则左下角,右上角的数分别为x+6,x-6.
由题意可得x+6+x+x-6=36,所以x=12,所以这9个数为4,5,6,11,12,13,18,19,20,
所以这9个数的和为 4+5 +6+11 +12+13+18+19+20=108,最后一天是20号.
(2)不能.理由:设正中间的数是m,
则m-8+m-7+m-6+m-1+m+m+1+m+6+m+7+m+8=216,
所以m=24,观察表格可知,24右下角没有日期,
所以方框不能圈出“总和为216”的9个数.
18.【解】(1)1 +2 +3 +4 +5 +6
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三章 整式及其加减
7 探索与表达规律
夯实基础逐点练
练点1 与图形有关的规律
1.一张长方形桌子需配6把椅子,按如图方式将桌子拼在一起,那么n张桌子需要配置的椅子把数为( )
A.2n+4 B.6+2n C.2n+8 D.6n
2.如图,用相同的圆点按照一定的规律拼出图形.第一幅图中有4个圆点,第二幅图中有7个圆点,第三幅图中有10个圆点,第四幅图中有13个圆点 按照此规律,第一百幅图中圆点的个数是( )
A.297 B.301 C.303 D.400
3.用正方形按如图所示的规律拼图案,其中第①个图案中有5个正方形,第②个图案中有9个正方形,第③个图案中有13个正方形,第④个图案中有17个正方形,按此规律排列下去,则第⑨个图案中正方形的个数为( )
A.32 B.34 C.37 D.41
练点2 与数或式有关的规律
4.观察下列数据: 则第 12个数是( )
5.有一列数:1,3,2,-1,…,其规律是从第二个数开始,每一个数都是其前后两个数之和,根据此规律,则第2024个数是( )
A.1 B.3 C.2 D.-1
练点3 与日历或数阵有关的规律
6.将正整数1至6 000 按一定规律排列如下表,同时平移表中带阴影的方框,方框中三个数的和可能是( )
A.116 B.117 C.129 D.138
7.将全体正偶数排成一个三角形数阵,按照如图所示的排列规律,第10行第5个数是( )
A.98 B.100 C.102 D.104
第7题图 第8题图
8.如图,以O 为端点画六条射线 OA,OB,OC,OD,OE,OF后,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为1,2,3,4,5,6,7,8,…,那么所描的第2024个点在射线_________上.
纠易错 找图形变化规律时易忽视图形重叠部分而导致重复计算
9.将灰、白两种颜色的正六边形地砖按如图所示的方式拼成若干个图案.
(1)第4个图案中有白色地砖____________块;
(2)第 n个图案中有白色地砖___________块.
整合方法提升练
10.将字母“C”,“H”按照如图所示的规律摆放,依次下去,则第④个图形中字母“H”的个数是( )
A.9 B.10 C.11 D.12
11.观察下列树枝分杈的规律图,若第 n个图中树枝数用 表示,则Y -Y =( )
A.15×2 B.31×2 C.33×2 D.63×2
12.观察下列等式:7°=1,7 =7,7 =49,7 =343,7 = 2401,7 =16807,…,根据其中的规律可得 7 的结果的个位数字是( )
A.0 B.1 C.7 D.8
13.下列图形是将等边三角形按一定规律排列,则第5个图形中所有等边三角形的个数是_____________.
14.将一列有理数 如图所示有序排列. 根据图中的排列规律可知,“峰1”中峰顶的位置(C的位置)是有理数4,那么“峰7”中C的位置是有理数_________,-103 应排在A,B,C,D,E中_____________的位置.
15.我们知道简便计算的好处,事实上,简便计算在好多地方都存在,观察下列等式:
15 =1×2×100 +25 =225,
25 =2×3×100 +25 =625,
35 =3×4×100+25 =1 225,
……
(1)根据上述等式反映出的规律填空:
95 =_______________=____________.
(2)设这类等式左边两位数的十位数字为a,请用一个含a的代数式表示其结果.
(3)这种简便计算也可以推广应用:个位数字是5的三位数的平方,请写出195 的简便计算过程及结果.
16.如图,正方形ABCD内部有若干个点,用这些点以及正方形 ABCD的顶点 A,B,C,D 把原正方形分割成一些三角形(互相不重叠).
(1)填写下表:
正方形ABCD内部点的个数 1 2 3 4 …
分割成的三角形的个数 4 6 …
(2)原正方形能否被分割成2 023个三角形 若能,求此时正方形 ABCD 内部有多少个点;若不能,请说明理由.
17.在如表所示2023年1月份日历中,用长方形的方框圈出任意3×3个数.
星期日 星期一 星期二 星期三 星期四 星期五 星期六
1 2 3 4 5 6 7
8 9 10 11 12 13 14
15 16 17 18 19 20 21
22 23 24 25 26 27 28
29 30 31
(1)如果从左下角到右上角的“对角线”上的3个数字的和为 36,那么这9个数的和为_____________.在这9个日期中,最后一天是___________号;
(2)在这个月的日历中,用方框能否圈出“总和为216”的9个数 如果能,请求出这9个日期正中间一天是几号;如果不能,请说明理由.
探究培优拓展练
18.式子 表示从1开始的连续 100个正整数的和,由于上述式子比较长,书写不方便,为了简便起见,可以将上述式子表示为 这里“∑”是求和的符号.例如 ’用“∑”可以表示为 用“∑”可以表示为
(1)把 写成加法的形式是____________;
用“∑”可以表示为_________;
(3)计算:
参考答案
1. A 【点拨】观察图形发现多一张桌子,则多2把椅子,所以n张桌子需要6+2(n-1)=2n+4(把)椅子.
2. B 【点拨】第一幅图中有4个圆点,4=4+3×0;第二幅图中有7个圆点,7=4+3=4+3×1;
第三幅图中有10个圆点,10=4+3+3=4+3×2;第四幅图中有13个圆点,13=4+3+3+3=4+3×3;…;那么第 n幅图中圆点的个数为4+3(n-1)=3n+1,所以第一百幅图中圆点的个数为 3×100+1=301.
3. C 【点拨】第①个图案中有5个正方形;
第②个图案中有9个正方形,9=5+4=5+4×1;
第③个图案中有13个正方形,13=5 +4+4=5+4×2;
第④个图案中有17个正方形,17=5+4+4+4=5+4×3;
…;
第n个图案中正方形的个数为5+4(n-1)=4n+1;
所以第⑨个图案中正方形的个数为4×9+1=37.
4. D【点拨】观察所给的数可知第 n个数是 所以第12个数是
5. B 【点拨】根据题意可知,这列数是1,3,2,-1,-3,-2,1,3,2,…,
发现1,3,2,-1,-3,-2,6个数一个循环,
因为 2 024÷6=337……2,所以第2024个数是3.
6. A 【点拨】设带阴影的方框中最小的数是x,则其他两个数是x+2,x+9,则x+x+2+x+9=3x+
11,令3x+11=116,则x=35;令3x+11=117,则 不是整数;令3x+11=129,则 不是整数;令3x+11=138,则 不是整数,所以和可能是116.
7. B【点拨】观察数字的变化可知,
第n行有n个偶数,
因为第1行的第1个数是2=1×0+2;
第2行的第1个数是4=2×1+2;
第3行的第1个数是8=3×2+2;…;
所以第n行的第1个数是 n(n-1)+2.
所以第10行第1个数是10×9+2=92,
所以第10行第5个数是92+2×4=100.
8. OB 【点拨】因为1在射线OA 上,2在射线OB上,3在射线OC上,4在射线OD上,5在射线OE上,6在射线OF上,7在射线OA上,…所以每6个数一个循环.
因为2024÷6=337 2,所以所描的第2024个点所在射线与2所在射线一样.
所以所描的第2024个点在射线OB上.
9.(1)18
(2)(4n+2)
【点拨】第1个图案中白色地砖的块数为4×1+2=6;
第2个图案中白色地砖的块数为4×2+2=10;
第3个图案中白色地砖的块数为4×3+2=14;
第4个图案中白色地砖的块数为4×4+2=18;
…;
第 n个图案中白色地砖的块数为 4n+2.
点易错 本题易错的原因是把第 n个图案当成由n个第1个图案组成,忽略了重叠部分.
10. B 【点拨】第①个图形中字母“H”的个数为4,
第②个图形中字母“H”的个数为4+2,
第③个图形中字母“H”的个数为4+2×2,
第④个图形中字母“H”的个数为4+2×3=10.
11. B 【点拨】由题图可得Y =1 =2 -1,Y =3=以此类推,可得 所以Y =2 -1,所以Y -Y =2 -1-2 +1 =31×2 .
12. B 【点拨】观察所给等式发现7"的个位数字按1,7,9,3 这4个数进行循环,
因为1+7+9+3=20,2 025÷4=506……1,所以 的结果的个位数字是1.
13.485 【点拨】第1个图形中有5个等边三角形,第2个图形中有5×3+2=17(个)等边三角形,第3个图形中有17×3+2=53(个)等边三角形,由此得出第4个图形中有53×3+2 =161(个)等边三角形,所以第5个图形中有161×3+2 =485(个)等边三角形.
14.34;B 【点拨】每五个数一个峰,且第奇数个峰中C的位置是正偶数,第偶数个峰中C的位置是负奇数,故“峰7”中C的位置是7×5-1=34.
因为(103-1)÷5=20……2,所以-103在B的位置.
15.【解】(1)9×10×100 +25;9 025
(2)(10a+5) =a·(a+1)×100 +25=100a(a+1)+25.
(3)195 =19×20×100+25=38 025.
16.【解】(1)8;10;2(n+1)
(2)不能.
设正方形ABCD内部有 a个点,则2(a+1)=2023,解得
因为 不是整数,所以原正方形不能被分割成2023个三角形.
17.【解】(1) 108;20 【点拨】设正中间的数是x,则左下角,右上角的数分别为x+6,x-6.
由题意可得x+6+x+x-6=36,所以x=12,所以这9个数为4,5,6,11,12,13,18,19,20,
所以这9个数的和为 4+5 +6+11 +12+13+18+19+20=108,最后一天是20号.
(2)不能.理由:设正中间的数是m,
则m-8+m-7+m-6+m-1+m+m+1+m+6+m+7+m+8=216,
所以m=24,观察表格可知,24右下角没有日期,
所以方框不能圈出“总和为216”的9个数.
18.【解】(1)1 +2 +3 +4 +5 +6
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
