15.5.2公式法(2)[下学期]
文档属性
| 名称 | 15.5.2公式法(2)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 808.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-01-08 18:23:00 | ||
图片预览





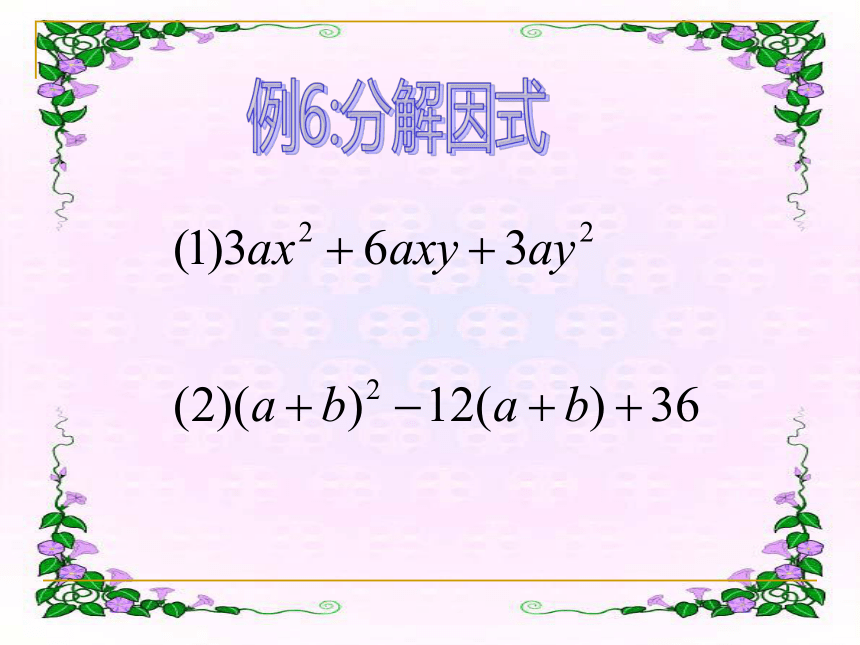
文档简介
课件12张PPT。15.5.2公式法(2)运用a2-b2=(a+b)(a-b) 分解因式一直到不能分解为止.所以分解后一定检查括号内是否能继续分解.温故知新 分解因式时有时要考虑综合运用各种方法,
例如:你会对x2-6x+9因式分解吗?探究完全平方公式公式应用的特征: 左边是:两数的平方和与这两数积的两倍
和(或差).右边是:这两数和(或差)的平方.例1:下列各多项式哪些能用完全平方公式因式分解?若能,请找出相应的a和b.例5:把下列各式因式分解例6:分解因式练习
1。下列多项式是不是完全平方式?为什么?
a2-4a+4; (2)1+4a2;
(3) 4b2+4b-1 ; (4)a2+ab+b2.2.分解因式:
(1) x2+12x+36; (2) -2xy-x2-y2;
(3) a2+2a+1; (4) 4x2-4x+1;
(5) ax2+2a2x+a3; (6) -3x2+6xy-3y2.例:简便方法运算。1,在括号内填上适当的代数式,使等式成立1,a2+6a+______=(a+____)22,16a2+_______+9b2=[___+ _____ ]293±24ab4a(±3b)推广与应用2,k-6ab+9b2是一个完全平方式,
那么的值是_____a2◆仔细做一做:
分解因式:
(x+y)2+4(x-y)2-4(x2-y2).◆创新应用:
已知(a+2b)2-2a-4b+1=0,求(a+2b)2005的值.◆综合拓展:
已知△ABC的三边分别为a,b,c,且a,b,c满足等式3(a2+b2+c2)=(a+b+c)2,请你说明△ABC是等边三角形.课堂小结:谈谈本节课你有哪些收获?
再见
例如:你会对x2-6x+9因式分解吗?探究完全平方公式公式应用的特征: 左边是:两数的平方和与这两数积的两倍
和(或差).右边是:这两数和(或差)的平方.例1:下列各多项式哪些能用完全平方公式因式分解?若能,请找出相应的a和b.例5:把下列各式因式分解例6:分解因式练习
1。下列多项式是不是完全平方式?为什么?
a2-4a+4; (2)1+4a2;
(3) 4b2+4b-1 ; (4)a2+ab+b2.2.分解因式:
(1) x2+12x+36; (2) -2xy-x2-y2;
(3) a2+2a+1; (4) 4x2-4x+1;
(5) ax2+2a2x+a3; (6) -3x2+6xy-3y2.例:简便方法运算。1,在括号内填上适当的代数式,使等式成立1,a2+6a+______=(a+____)22,16a2+_______+9b2=[___+ _____ ]293±24ab4a(±3b)推广与应用2,k-6ab+9b2是一个完全平方式,
那么的值是_____a2◆仔细做一做:
分解因式:
(x+y)2+4(x-y)2-4(x2-y2).◆创新应用:
已知(a+2b)2-2a-4b+1=0,求(a+2b)2005的值.◆综合拓展:
已知△ABC的三边分别为a,b,c,且a,b,c满足等式3(a2+b2+c2)=(a+b+c)2,请你说明△ABC是等边三角形.课堂小结:谈谈本节课你有哪些收获?
再见
