15.5.2公式法(1)[上学期]
文档属性
| 名称 | 15.5.2公式法(1)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 245.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-17 15:11:00 | ||
图片预览








文档简介
课件28张PPT。15.5.2公式法(1)问题1:什么叫多项式的因式分解?把一个多项式写成几个整式积的形式叫做多项式的因式分解把下列各式分解因式:
⑴4a2b-2ab
⑵-3x3y+6x2-9x
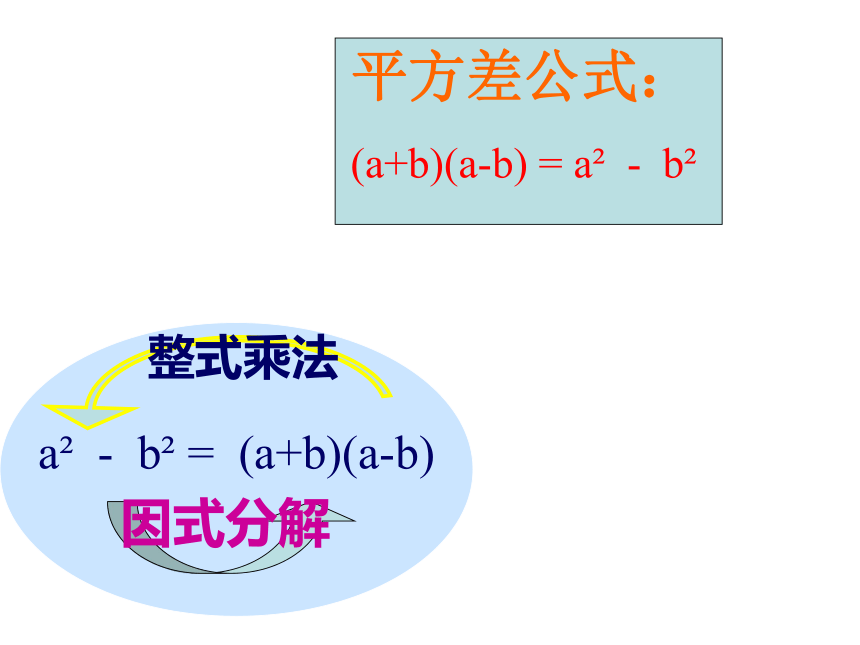
=2ab(2a-1)=-3x(x2y-2x+3)(3)2(a+b)2-(a+b)=(a+b)[2(a+b)-1]=(a+b)(2a+2b-1)创设情境引入 9992-1是1000的倍数吗?计算下列各式: (a+2)(a-2) =_____________.(2) (3a+2b)(3a-2b) =___________.a2-49a2-4b22. 根据上面的算式填空:(1) a2-4 =_________________.(2) 9a2-4b2 =________________.(a+2)(a-2)(3a+2b)(3a-2b)平方差公式:
(a+b)(a-b) = a2 - b2
a2 - b2 = (a+b)(a-b)
整式乘法
因式分解
a2-b2=(a+b)(a-b)两个数平方差,等于这两个数的和与这两个数的差的积。公式的结构特征:(1)左边是二项式,每项都是平方的形式,两项的符号相反;(2)右边是两个多项式的积,一个因式是两数的和,另一个因式是这两数的差;因式分解(1) X2 – 9例1. 把下列各式分解因式.(2) 4X2 – 9y2(3)4a6X2 – 9b4y2= x2-32=(x+3)(x-3)=( )2- ( )2=( + )( - )=(2a3x+3b2y)(2a3x-3b2y)2x3ya2 - b2 = ( a + b) (a - b)3y2x3y2x=( )2 - ( )22a3x3b2y(4) –9b4y2+ 4a6X2= 4a6X2 – 9b4y2=(2a3x)2- (3b2y)2=(2a3x+3b2y)(2a3x-3b2y)(1)9a2 - 4b2轻松闯关:(2) –x2y2+z2(3)快乐练习:下列各式能否用平方差公式分解?
①x2+y2
② x2-y2
③ -x2+y2
④ -x2-y2=(x+y)(x-y)=y2-x2=(y+x)(y-x)例2 分解因式:
(1)(x+m)2- (x+n)2=[( ) + ( )][( ) - ( )]
注意:a2-b2=(a+b)(a-b)中的a、b可以是一个数、一个单项式也可以是一个多项式。
=(2x+m+n)(m-n)x+mx+nx+mx+n =(x+m+x+n)(x+m-x-n)例2 分解因式:
(1)(x+m)2- (x+n)2(2)25(x+m)2-16(x+n)2=[ ]2-[ ]2 =[ + ][ - ]=(5x+5m+4x+4n)(5x+5m-4x-4n)=(9x+5m+4n)(x+5m-4n)
5(x+m)4(x+n)]4(x+n)5(x+m)5(x+m)4(x+n)例2 分解因式:
(1)(x+m)2- (x+n)2(2)25(x+m)2-16(x+n)2(3) - 16x2+ (x- y)2①x4-y4 ②a3b-ab解:①x4-y4 =(x2)2-(y2)2=(x2+y2)(x2-y2)=(x2+y2)(x+y)(x-y)② a3b-ab =ab(a2-1)=ab(a+1)(a-1)分解因式,必须进行到每一个多项式都不能再分解为止。例3 分解因式:(a- b)n- (a- b)n+2③③(a- b)n- (a- b)n+2=(a- b)n [1- (a- b) 2 ]=(a- b)n [1+ (a- b) ] [1- (a- b) ]=(a- b)n (1+ a- b ) (1- a+ b)融会贯通因式分解:
1、 – a4 + 16
2、 4(a+2)2 - 9(a - 1)2
3、 8x5-2x34、a2(x-1)+b2(1-x)知识应用 9992-1==1000×9989992-12=(999+1) (999-1)所以 9992-1 是1000的倍数. 9992-1是1000的倍数吗? 如图,求圆环形绿化区的面积. 解: 352 -152= (352-152)=(35+15)(35-15)=50×20
=1000 (m2)这个绿化区的面积是1000 m2
思考探索 观察下列各式:1–9 = - 8, 4-16= -12,
9-25=-16, 16-36= -20 ······
(1)猜想以上各式所含的规律,用含n(n为正整数) 的等式表示出来。
(2)试证明你的猜想4.运用平方差公式分解因式时,
要注意步骤与要点. 小结:
1.因式分解的步骤是首先提取公因式,然后考虑用公式.
2.因式分解进行到每一个因式不能分解为止.
3.计算中应用因式分解,可使计算简便.2、设n为整数,用因式分解说明(2n+1)2 - 25能被4整除。1、运用简便方法计算:
1) 20032 – 9
2)(1 - )(1 - )(1- )×···×(1- )(1- )
综合运用3、若a、b、c是三角形的三边长且满足
(a+b)2-(a+c)2=0,则此三角形是( )
A、等腰三角形 B、等边三角形
C、直角三角形 D、不能确定
利用因式分解计算:
1002-992+982-972+962-952+… +22-12解:原式=(100+99)(100-99)+(98+97)(98-97) +… +(2+1)(2-1)
挑战自我练习:因式分解(1)16x2-9y2
(2)-a4+16
(3)4(a+2)2-9(a-1)2
(4)x5-x3
(5)(x-1)+b2(1-x)解:(1)(2)x2n+1-100x
= x(x2n-100)
= x(xn+10)(xn-10)
不可以可 以不可以可 以不可以可 以
思考探索 观察下列各式:1–9 = - 8, 4-16= -12,
9-25=-16, 16-36= -20 ······
(1)把以上各式所含的规律用含n(n为正整数)的等式表示出来。
(2)按照(1)中的规律,请写出第 10个等式。若a=101,b=99,求a2-b2的值.把下列各式分解因式:
⑴4a2b-2ab
⑵-3x3y+6x2-9x
=2ab(2a-1)=-3x(x2y-2x+3)(3)2(a+b)2-(a+b)=(a+b)[2(a+b)-1](4) ax2 - a3=a(x2-a2)=a(x+a)(x-a)=(a+b)(2a+2b-1)
⑴4a2b-2ab
⑵-3x3y+6x2-9x
=2ab(2a-1)=-3x(x2y-2x+3)(3)2(a+b)2-(a+b)=(a+b)[2(a+b)-1]=(a+b)(2a+2b-1)创设情境引入 9992-1是1000的倍数吗?计算下列各式: (a+2)(a-2) =_____________.(2) (3a+2b)(3a-2b) =___________.a2-49a2-4b22. 根据上面的算式填空:(1) a2-4 =_________________.(2) 9a2-4b2 =________________.(a+2)(a-2)(3a+2b)(3a-2b)平方差公式:
(a+b)(a-b) = a2 - b2
a2 - b2 = (a+b)(a-b)
整式乘法
因式分解
a2-b2=(a+b)(a-b)两个数平方差,等于这两个数的和与这两个数的差的积。公式的结构特征:(1)左边是二项式,每项都是平方的形式,两项的符号相反;(2)右边是两个多项式的积,一个因式是两数的和,另一个因式是这两数的差;因式分解(1) X2 – 9例1. 把下列各式分解因式.(2) 4X2 – 9y2(3)4a6X2 – 9b4y2= x2-32=(x+3)(x-3)=( )2- ( )2=( + )( - )=(2a3x+3b2y)(2a3x-3b2y)2x3ya2 - b2 = ( a + b) (a - b)3y2x3y2x=( )2 - ( )22a3x3b2y(4) –9b4y2+ 4a6X2= 4a6X2 – 9b4y2=(2a3x)2- (3b2y)2=(2a3x+3b2y)(2a3x-3b2y)(1)9a2 - 4b2轻松闯关:(2) –x2y2+z2(3)快乐练习:下列各式能否用平方差公式分解?
①x2+y2
② x2-y2
③ -x2+y2
④ -x2-y2=(x+y)(x-y)=y2-x2=(y+x)(y-x)例2 分解因式:
(1)(x+m)2- (x+n)2=[( ) + ( )][( ) - ( )]
注意:a2-b2=(a+b)(a-b)中的a、b可以是一个数、一个单项式也可以是一个多项式。
=(2x+m+n)(m-n)x+mx+nx+mx+n =(x+m+x+n)(x+m-x-n)例2 分解因式:
(1)(x+m)2- (x+n)2(2)25(x+m)2-16(x+n)2=[ ]2-[ ]2 =[ + ][ - ]=(5x+5m+4x+4n)(5x+5m-4x-4n)=(9x+5m+4n)(x+5m-4n)
5(x+m)4(x+n)]4(x+n)5(x+m)5(x+m)4(x+n)例2 分解因式:
(1)(x+m)2- (x+n)2(2)25(x+m)2-16(x+n)2(3) - 16x2+ (x- y)2①x4-y4 ②a3b-ab解:①x4-y4 =(x2)2-(y2)2=(x2+y2)(x2-y2)=(x2+y2)(x+y)(x-y)② a3b-ab =ab(a2-1)=ab(a+1)(a-1)分解因式,必须进行到每一个多项式都不能再分解为止。例3 分解因式:(a- b)n- (a- b)n+2③③(a- b)n- (a- b)n+2=(a- b)n [1- (a- b) 2 ]=(a- b)n [1+ (a- b) ] [1- (a- b) ]=(a- b)n (1+ a- b ) (1- a+ b)融会贯通因式分解:
1、 – a4 + 16
2、 4(a+2)2 - 9(a - 1)2
3、 8x5-2x34、a2(x-1)+b2(1-x)知识应用 9992-1==1000×9989992-12=(999+1) (999-1)所以 9992-1 是1000的倍数. 9992-1是1000的倍数吗? 如图,求圆环形绿化区的面积. 解: 352 -152= (352-152)=(35+15)(35-15)=50×20
=1000 (m2)这个绿化区的面积是1000 m2
思考探索 观察下列各式:1–9 = - 8, 4-16= -12,
9-25=-16, 16-36= -20 ······
(1)猜想以上各式所含的规律,用含n(n为正整数) 的等式表示出来。
(2)试证明你的猜想4.运用平方差公式分解因式时,
要注意步骤与要点. 小结:
1.因式分解的步骤是首先提取公因式,然后考虑用公式.
2.因式分解进行到每一个因式不能分解为止.
3.计算中应用因式分解,可使计算简便.2、设n为整数,用因式分解说明(2n+1)2 - 25能被4整除。1、运用简便方法计算:
1) 20032 – 9
2)(1 - )(1 - )(1- )×···×(1- )(1- )
综合运用3、若a、b、c是三角形的三边长且满足
(a+b)2-(a+c)2=0,则此三角形是( )
A、等腰三角形 B、等边三角形
C、直角三角形 D、不能确定
利用因式分解计算:
1002-992+982-972+962-952+… +22-12解:原式=(100+99)(100-99)+(98+97)(98-97) +… +(2+1)(2-1)
挑战自我练习:因式分解(1)16x2-9y2
(2)-a4+16
(3)4(a+2)2-9(a-1)2
(4)x5-x3
(5)(x-1)+b2(1-x)解:(1)(2)x2n+1-100x
= x(x2n-100)
= x(xn+10)(xn-10)
不可以可 以不可以可 以不可以可 以
思考探索 观察下列各式:1–9 = - 8, 4-16= -12,
9-25=-16, 16-36= -20 ······
(1)把以上各式所含的规律用含n(n为正整数)的等式表示出来。
(2)按照(1)中的规律,请写出第 10个等式。若a=101,b=99,求a2-b2的值.把下列各式分解因式:
⑴4a2b-2ab
⑵-3x3y+6x2-9x
=2ab(2a-1)=-3x(x2y-2x+3)(3)2(a+b)2-(a+b)=(a+b)[2(a+b)-1](4) ax2 - a3=a(x2-a2)=a(x+a)(x-a)=(a+b)(2a+2b-1)
