2022-2023学年九年级上册人教版数学第二十四章圆单元测试(含答案)
文档属性
| 名称 | 2022-2023学年九年级上册人教版数学第二十四章圆单元测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 158.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-04 00:00:00 | ||
图片预览



文档简介
第二十四章 圆 单元测试 2022-2023学年九年级上册人教版数学
一、单选题
1.如L是⊙O的切线,要判定AB⊥L,还需要添加的条件是( )
A.AB经过圆心O B.AB是直径
C.AB是直径,B是切点 D.AB是直线,B是切点
2.如图,在⊙中,直径垂直于弦,若,则的度数是( )
A. B. C. D.
3.如图, 的半径 垂直于弦 于点 ,连接 并延长交 于点 ,连接 .若 ,,则 的长为( )
A. B. C. D.
4.如图在Rt△ABC中,∠ACB=90°,AC=6,BC=8,⊙O是△ABC的内切圆,连接AO,BO.则图中阴影部分的面积之和( )
A. B. C.12 D.14
5.如图,点 ,, 在 上,若 ,则 的度数是
A. B. C. D.
6.如图,在半径为 的 中,, 是互相垂直的两条弦,垂足为 ,且 ,则 的长为
A. B. C. D.
7.如图,已知 为 的半径,且 ,弦 于 ,若 ,则 长为
A. B. C. D.
8.如图,在平面直角坐标系中, 与 轴相切于原点 ,平行于 轴的直线交 于 , 两点,点 在点 的右方,若点 的坐标是 ,则点 的坐标是
A. B. C. D.
二、填空题
9.如图,一扇形纸扇完全打开后,外侧两竹条 和 的夹角为 , 长为 ,贴纸部分的宽 为 ,若纸扇两面贴纸,则贴纸的面积为 .(结果保留 )
10.在半径为 的圆中, 的圆心角所对的弧长等于 .
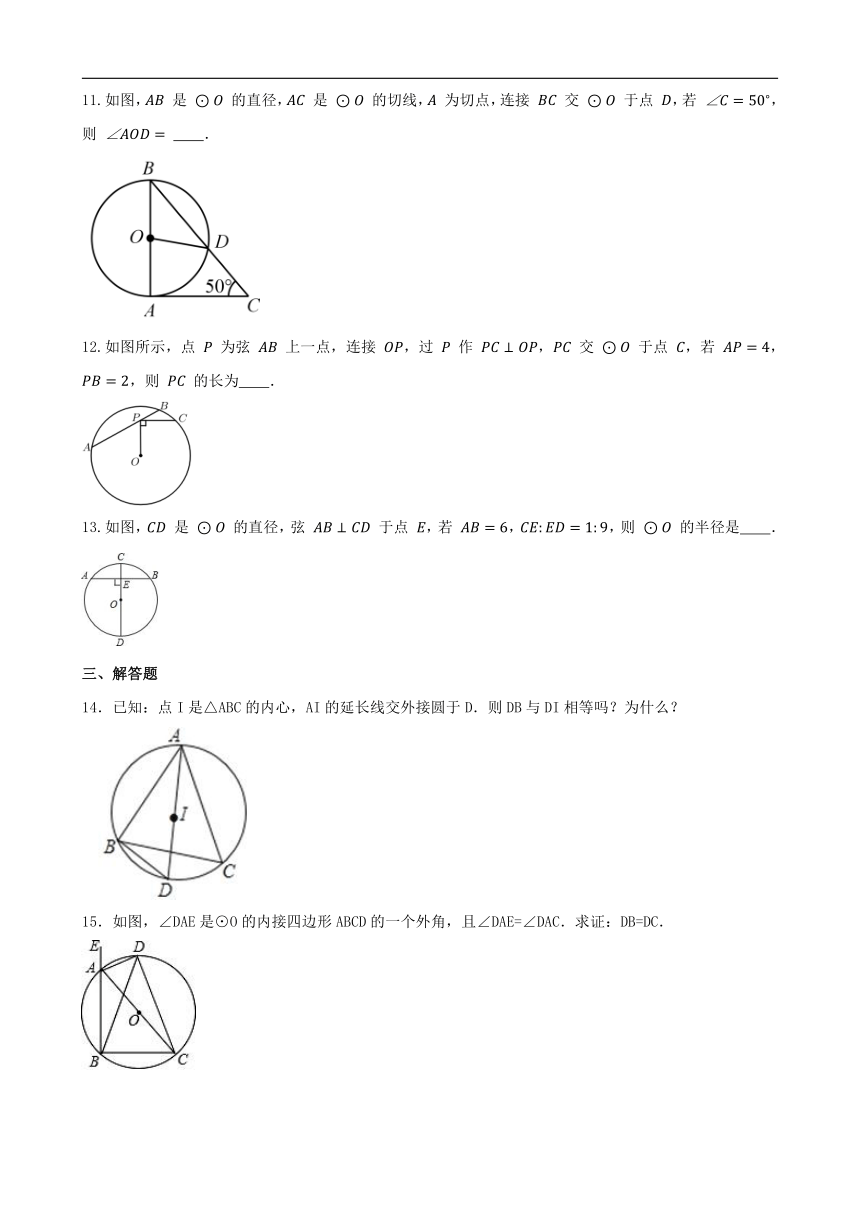
11.如图, 是 的直径, 是 的切线, 为切点,连接 交 于点 ,若 ,则 .
12.如图所示,点 为弦 上一点,连接 ,过 作 , 交 于点 ,若 ,,则 的长为 .
13.如图, 是 的直径,弦 于点 ,若 ,,则 的半径是 .
三、解答题
14.已知:点I是△ABC的内心,AI的延长线交外接圆于D.则DB与DI相等吗?为什么?
15.如图,∠DAE是⊙O的内接四边形ABCD的一个外角,且∠DAE=∠DAC.求证:DB=DC.
16.如图,AD是⊙O的弦,AB经过圆心O交⊙O于点C,∠A=∠B=30°,连接BD.求证:BD是⊙O的切线.
17.如图,四边形ABCD是⊙O的内接四边形,AD的延长线与BC的延长线相交于点E,DC=DE.
(1)求证:∠A=∠AEB;
(2)如果DC⊥OE,求证:△ABE是等边三角形.
18.如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,OA=5,AB与⊙O相切于点B,BP的延长线交直线l于点C.
(1)求证:AB=AC.
(2)若PC=2 ,求⊙O的半径.
参考答案
1.C
2.A
3.C
4.B
5. B
6. C
7. C
8. A
9.
10.
11.
12.
13.
14.解:ID=BD.
理由:如图所示:连接BI.
由三角形的外角的性质可知:∠1+∠2=∠BIA.
∵点I是△ABC的内心,
∴∠1=∠4,∠2=∠3.
又∵∠4=∠5,
∴∠1+∠2=∠3+∠4=∠3+∠5,即∠BIA=∠IBD.
∴ID=BD.
15.证明:∵∠DAE是⊙O的内接四边形ABCD的一个外角,∴∠DAE=∠DCB,又∠DAE=∠DAC,∴∠DCB=∠DAC,又∠DAC=∠DBC,∴∠DCB=∠DBC,∴DB=DC
16.解:如图,连接OD,
∵OD=OA,
∴∠ODA=∠DAB=30°,
∴∠DOB=∠ODA+∠DAB=60°,
∴∠ODB=180°﹣∠DOB﹣∠B=180°﹣60°﹣30°=90°,
即OD⊥BD,
∴直线BD与⊙O相切.
17.(1)证明:∵四边形ABCD是⊙O的内接四边形,
∴∠A=∠DCE,
∵DC=DE,
∴∠DCE=∠DEC,
∴∠A=∠AEB
(2)证明:∵DC⊥OE,
∴DF=CF,
∴OE是CD的垂直平分线,
∴ED=EC,又DE=DC,
∴△DEC为等边三角形,
∴∠AEB=60°,又∠A=∠AEB,
∴△ABE是等边三角形.
18.(1)证明:连接OB,
∵OB=OP,
∴∠OPB=∠OBP,
∵∠OPB=∠APC,
∴∠OBP=∠APC,
∵AB与⊙O相切于点B,
∴OB⊥AB,
∴∠ABO=90°,
∴∠ABP+∠OBP=90°,
∵OA⊥AC,
∴∠OAC=90°,
∴∠ACB+∠APC=90°,
∴∠ABP=∠ACB,
∴AB=AC
(2)证明:设⊙O的半径为r,
在Rt△AOB中,AB2=OA2﹣OB2=52﹣r2,
在Rt△ACP中,AC2=PC2﹣PA2,
AC2=(2 )2﹣(5﹣r)2,
∵AB=AC,
∴52﹣r2=(2 )2﹣(5﹣r)2,
解得:r=3,
则⊙O的半径为3
一、单选题
1.如L是⊙O的切线,要判定AB⊥L,还需要添加的条件是( )
A.AB经过圆心O B.AB是直径
C.AB是直径,B是切点 D.AB是直线,B是切点
2.如图,在⊙中,直径垂直于弦,若,则的度数是( )
A. B. C. D.
3.如图, 的半径 垂直于弦 于点 ,连接 并延长交 于点 ,连接 .若 ,,则 的长为( )
A. B. C. D.
4.如图在Rt△ABC中,∠ACB=90°,AC=6,BC=8,⊙O是△ABC的内切圆,连接AO,BO.则图中阴影部分的面积之和( )
A. B. C.12 D.14
5.如图,点 ,, 在 上,若 ,则 的度数是
A. B. C. D.
6.如图,在半径为 的 中,, 是互相垂直的两条弦,垂足为 ,且 ,则 的长为
A. B. C. D.
7.如图,已知 为 的半径,且 ,弦 于 ,若 ,则 长为
A. B. C. D.
8.如图,在平面直角坐标系中, 与 轴相切于原点 ,平行于 轴的直线交 于 , 两点,点 在点 的右方,若点 的坐标是 ,则点 的坐标是
A. B. C. D.
二、填空题
9.如图,一扇形纸扇完全打开后,外侧两竹条 和 的夹角为 , 长为 ,贴纸部分的宽 为 ,若纸扇两面贴纸,则贴纸的面积为 .(结果保留 )
10.在半径为 的圆中, 的圆心角所对的弧长等于 .
11.如图, 是 的直径, 是 的切线, 为切点,连接 交 于点 ,若 ,则 .
12.如图所示,点 为弦 上一点,连接 ,过 作 , 交 于点 ,若 ,,则 的长为 .
13.如图, 是 的直径,弦 于点 ,若 ,,则 的半径是 .
三、解答题
14.已知:点I是△ABC的内心,AI的延长线交外接圆于D.则DB与DI相等吗?为什么?
15.如图,∠DAE是⊙O的内接四边形ABCD的一个外角,且∠DAE=∠DAC.求证:DB=DC.
16.如图,AD是⊙O的弦,AB经过圆心O交⊙O于点C,∠A=∠B=30°,连接BD.求证:BD是⊙O的切线.
17.如图,四边形ABCD是⊙O的内接四边形,AD的延长线与BC的延长线相交于点E,DC=DE.
(1)求证:∠A=∠AEB;
(2)如果DC⊥OE,求证:△ABE是等边三角形.
18.如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,OA=5,AB与⊙O相切于点B,BP的延长线交直线l于点C.
(1)求证:AB=AC.
(2)若PC=2 ,求⊙O的半径.
参考答案
1.C
2.A
3.C
4.B
5. B
6. C
7. C
8. A
9.
10.
11.
12.
13.
14.解:ID=BD.
理由:如图所示:连接BI.
由三角形的外角的性质可知:∠1+∠2=∠BIA.
∵点I是△ABC的内心,
∴∠1=∠4,∠2=∠3.
又∵∠4=∠5,
∴∠1+∠2=∠3+∠4=∠3+∠5,即∠BIA=∠IBD.
∴ID=BD.
15.证明:∵∠DAE是⊙O的内接四边形ABCD的一个外角,∴∠DAE=∠DCB,又∠DAE=∠DAC,∴∠DCB=∠DAC,又∠DAC=∠DBC,∴∠DCB=∠DBC,∴DB=DC
16.解:如图,连接OD,
∵OD=OA,
∴∠ODA=∠DAB=30°,
∴∠DOB=∠ODA+∠DAB=60°,
∴∠ODB=180°﹣∠DOB﹣∠B=180°﹣60°﹣30°=90°,
即OD⊥BD,
∴直线BD与⊙O相切.
17.(1)证明:∵四边形ABCD是⊙O的内接四边形,
∴∠A=∠DCE,
∵DC=DE,
∴∠DCE=∠DEC,
∴∠A=∠AEB
(2)证明:∵DC⊥OE,
∴DF=CF,
∴OE是CD的垂直平分线,
∴ED=EC,又DE=DC,
∴△DEC为等边三角形,
∴∠AEB=60°,又∠A=∠AEB,
∴△ABE是等边三角形.
18.(1)证明:连接OB,
∵OB=OP,
∴∠OPB=∠OBP,
∵∠OPB=∠APC,
∴∠OBP=∠APC,
∵AB与⊙O相切于点B,
∴OB⊥AB,
∴∠ABO=90°,
∴∠ABP+∠OBP=90°,
∵OA⊥AC,
∴∠OAC=90°,
∴∠ACB+∠APC=90°,
∴∠ABP=∠ACB,
∴AB=AC
(2)证明:设⊙O的半径为r,
在Rt△AOB中,AB2=OA2﹣OB2=52﹣r2,
在Rt△ACP中,AC2=PC2﹣PA2,
AC2=(2 )2﹣(5﹣r)2,
∵AB=AC,
∴52﹣r2=(2 )2﹣(5﹣r)2,
解得:r=3,
则⊙O的半径为3
同课章节目录
