画图复习[上学期]

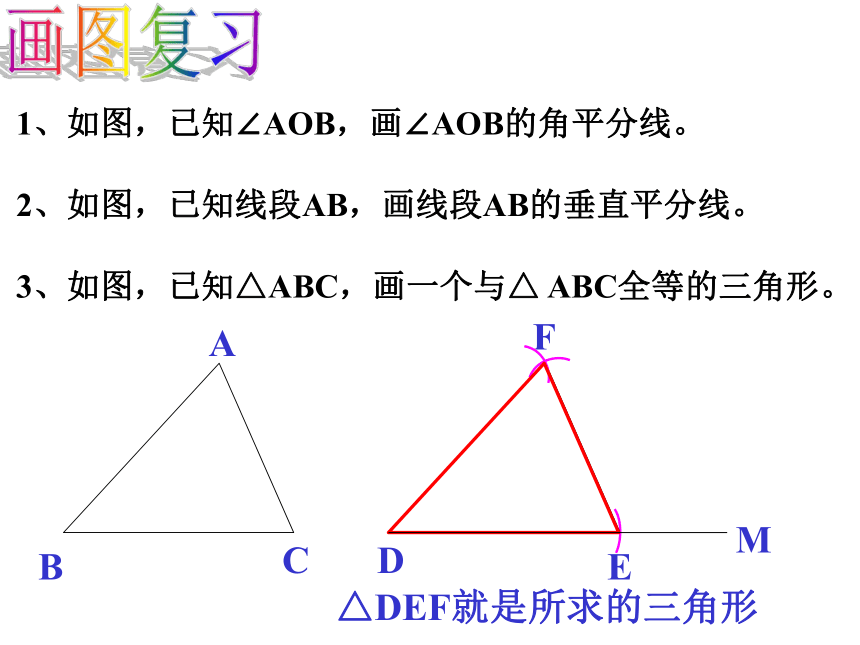
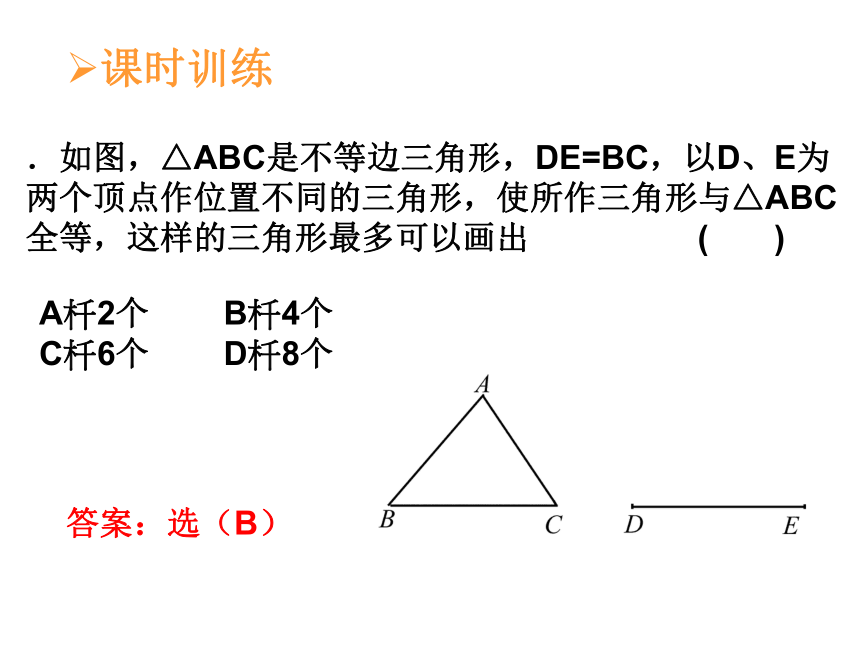
课件17张PPT。画图复习3、如图，已知△ABC，画一个与△ ABC全等的三角形。FE△DEF就是所求的三角形1、如图，已知∠AOB，画∠AOB的角平分线。2、如图，已知线段AB，画线段AB的垂直平分线。．如图，△ABC是不等边三角形，DE=BC，以D、E为两个顶点作位置不同的三角形，使所作三角形与△ABC全等，这样的三角形最多可以画出 ( )A?2个 B?4个
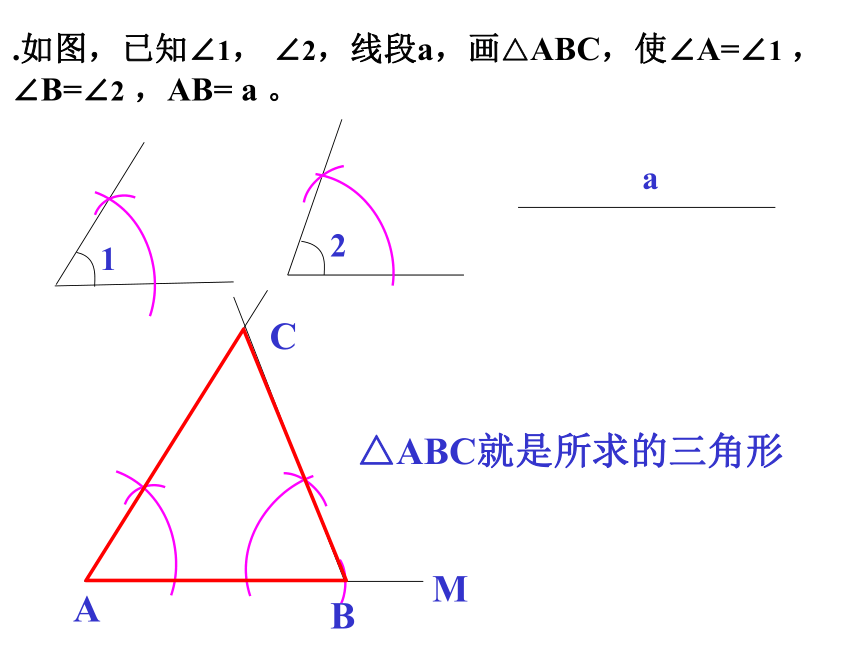
C?6个 D?8个答案：选（B）课时训练.如图，已知∠1， ∠2，线段a，画△ABC，使∠A=∠1 ，
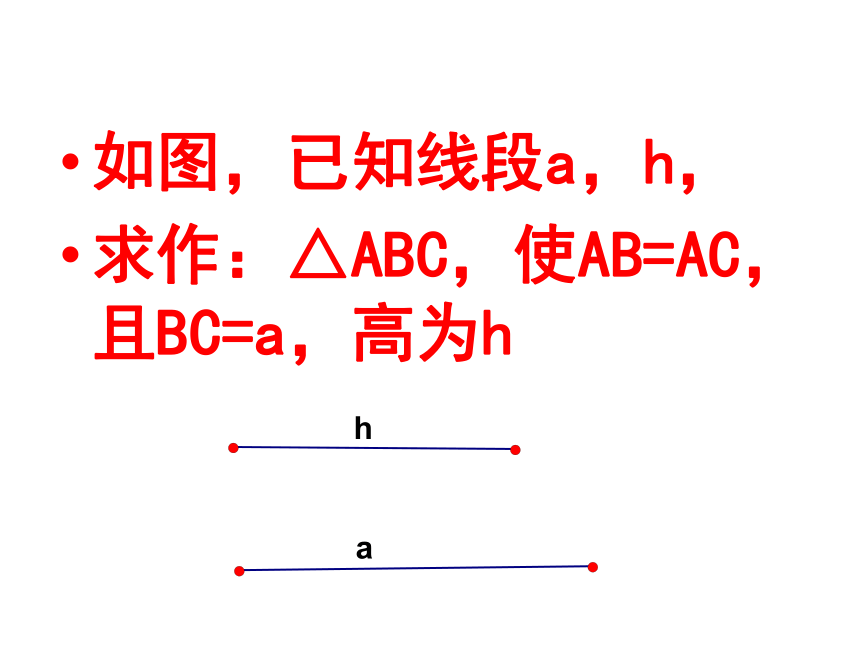
∠B=∠2 ，AB= a 。12aBC△ABC就是所求的三角形如图，已知线段a，h，
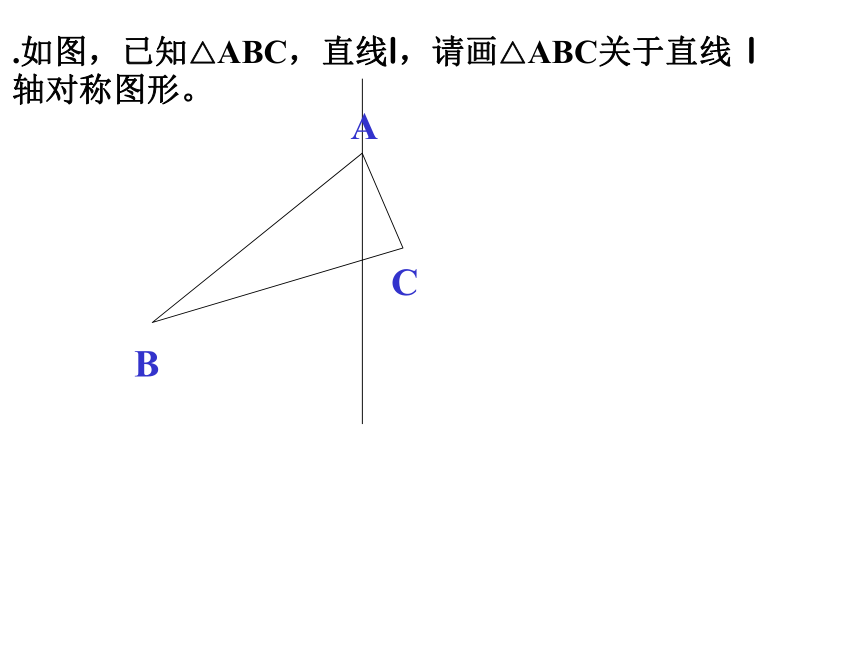
求作：△ABC，使AB=AC，且BC=a，高为h.如图，已知△ABC，直线l，请画△ABC关于直线 l
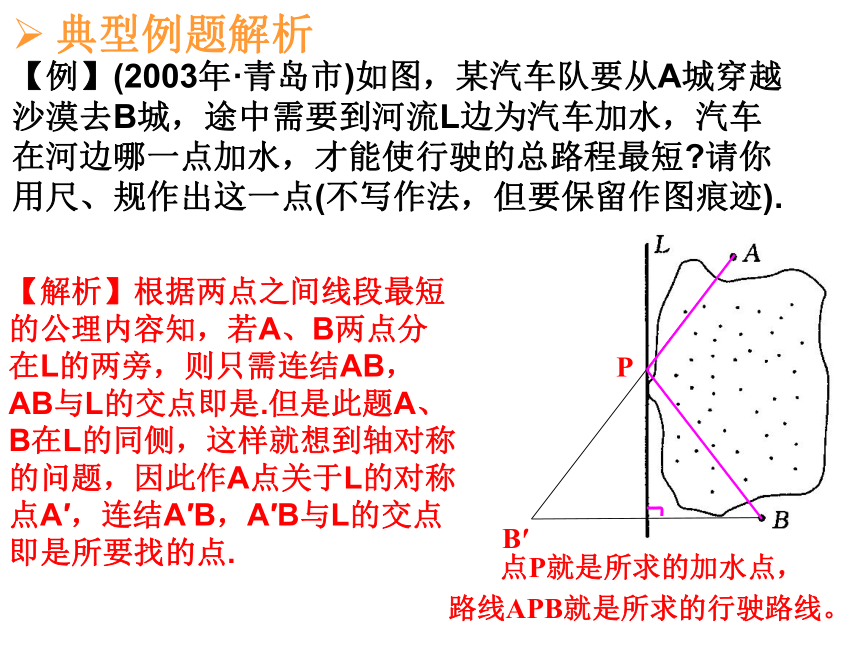
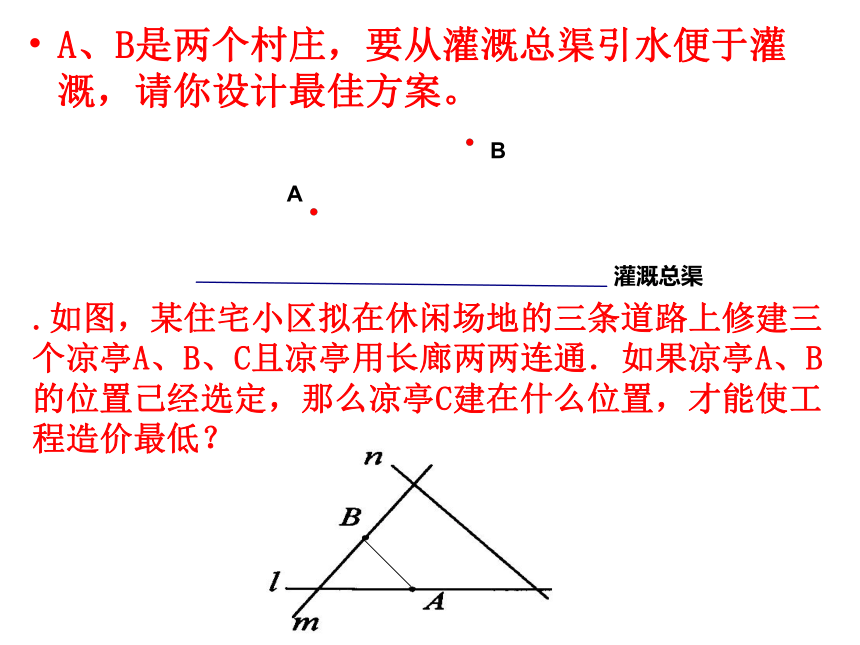
轴对称图形。ABC【例】(2003年·青岛市)如图，某汽车队要从A城穿越沙漠去B城，途中需要到河流L边为汽车加水，汽车在河边哪一点加水，才能使行驶的总路程最短?请你用尺、规作出这一点(不写作法，但要保留作图痕迹).典型例题解析【解析】根据两点之间线段最短的公理内容知，若A、B两点分在L的两旁，则只需连结AB，AB与L的交点即是.但是此题A、B在L的同侧，这样就想到轴对称的问题，因此作A点关于L的对称点A′，连结A′B，A′B与L的交点即是所要找的点. B′P点P就是所求的加水点，路线APB就是所求的行驶路线。A、B是两个村庄，要从灌溉总渠引水便于灌溉，请你设计最佳方案。.如图，某住宅小区拟在休闲场地的三条道路上修建三个凉亭A、B、C且凉亭用长廊两两连通．如果凉亭A、B的位置己经选定，那么凉亭C建在什么位置，才能使工程造价最低？.小林参加了这样的游戏，在活动区域边放了一些球（如图），在另一侧放着一些小木棍，小林应按怎样的路线跑去捡哪个位置的球、小木棍，才能最快跑到目的地A？你能说说为什么吗？··FEpQ小林按路线BPQA才能最快跑到目的地.已知三个自然村A、B、C的位置如图所示,现计划建一所小学,使其到A、B、C三个自然村的距离相等,请你设计出学校所在的位置O, .如图所示,为三条交叉公路,请你设计一个方案,在它们交叉的内部选址,建个物流中心O,使它到三条公路的距离相等,这样的地址有几处?请你画出来( 不用写画法,但要保留作图痕迹),并说明其中的理由.．(2003年·湖南省湘潭市)如图，国道107和国道320相交于O点，在∠AOB的内部有工厂C和D，现在修建一个货站P，使P到OA、OB的距离相等，且使PC=PD，用尺规作出货站P的位置(不写作法，保留作图痕迹，写出结论).课前热身P点P就是所求货站的位置课时训练.某村为合理使用土地，规划将住宅集中于A、B、C三个小区如图，为此需修建一座净化河水的自来水设施，(1)用尺、规作图，说明自来水设施建于何处，与三个小区等距离?(2)若直线l为河岸，作图说明水泵站建在何处才能使得向自来水设施铺设的管路最短?.已知，如图，△ABC中，AB=AC，∠A=360，仿照图（1），请你再设计两种不同的分法，将△ABC分割成3个三角形，使得每个三角形都是等腰三角形，（图（2）、图（3）供画图用，作图工具不限，不要求写出画法，不要求证明；要求标出所分得的每个等腰三角形三个内角的度数）如图，已知D是等腰三角形ABC底边BC上一点，
它到两腰AB、AC的距离分别为DE、DF。请你
指出当D点在什么位置时，DE=DF？并加以证明。例1已知等腰△ABC，由顶点A引BC边上的高恰好
等于BC边的一半。
（1）当BC为底边时，求∠A的度数；
（2）当BC为腰，且由顶点A引BC边上的高在
△ABC内部时，求∠A的度数；
（3）当BC为腰，且由顶点A引BC边上的高在
△ABC外部时，求∠A的度数。 1.有12棵树，把它栽成三排，要求每排恰好为5棵，
请你设计符合条件的栽法。（画出图形即可） 2.下列条件：(1)已知两腰；(2)已知底边和顶角；
（3）已知顶角和底角；(4)已知底边和底边上的
高。能确定一个等腰三角形的是（ ）
（A）（1）和（2） （B）（3）和（4）
（C）（2）和（4） （D）（1）和（4） 3.小颖从镜子里看到镜子对面电子钟的像如图所示，
则实际时间是（ ）
（A）21∶10 （B）10∶21
（C）10∶51 （D）12∶01
4.如图，在等边三角形ABC中，AD=BE=CF，
AE、BF、CD分别交于G、M、N，如果把
三个全等的三角形叫做一组全等三角形，
则图中有全等三角形（ ）
（A）6组 （B）5组
（C）4组 （D）3组 再见！