三角形的边[上学期]
图片预览









文档简介
课件59张PPT。三角形的边
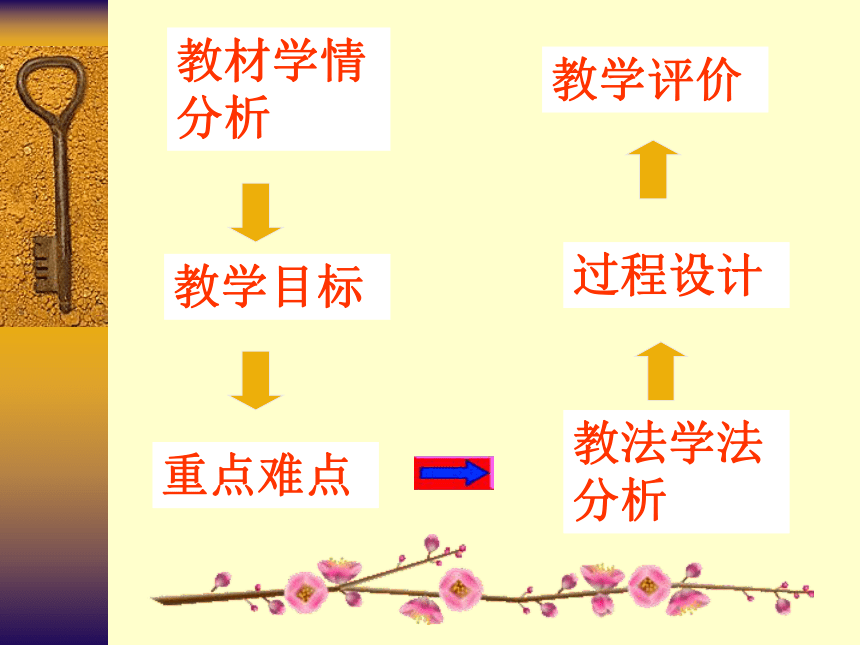
(说 课) 人教版七年级数学下册§7.1教法学法分析教材学情分析教学目标过程设计重点难点教学评价一、教材分析及学情分析1、教材的地位与作用2、学情分析 本节课是七年级下第七章的第一节,学生在小
学已学过一些三角形的知识,在前面学过线段、
角以及相交线、平行线等知识。他们的空间观念
得到进一步的发展,这样再来学习三角形的有关
内容,就有了更为充实的基础和准备。通过本节
的学习,可以丰富和加深学生对三角形边的认识。
同时为学习三角形的其他知识打好基础。起到了
承上启下的作用。教材分析一、教材分析及学情分析1、教材的地位与作用2、学情分析学情分析 在正式学习三角形三边关系之前,学生在生活
中已经积累了很多关于三角形三边关系的感性经验,
这些经验构成了学生学习的认知基础。教学过程中,
学生在抽象概括三角形三边之间的关系时,可能在
数学语言的描述上会有一定的困难,表达上也可能
不够严密,但只要学生表达的意思对,教师就应该
积极的给以肯定,同时教师要给学生更多探讨的空
间和交流的机会,毕竟数学模型的建立和思维的发
展需要经历一个渐近思辩的过程。 教法学法分析教材学情分析教学目标过程设计重点难点教学评价1、知识与技能目标2、过程与方法目标3、情感、态度与价值观目标二、教学目标知识目标 认识三角形,了解三角形的意义,认识三角
形的边、内角、顶点,能用符号语言表示三
角形. 1.经历度量三角形边长的实践活动中,理解三角形三边不等的关系.
2.懂得判断三条线段可否构成一个三角形的方法,并能运用它解决有关的问题.能力目标情感目标 帮助学生树立几何知识源于客观实际,用客观
实际的观念,激发学生学习的兴趣.教法学法分析教材学情分析教学目标过程设计重点难点教学评价教学重点 1.对三角形有关概念的了解,能用符号语
言表示三条形.
2.能从图中识别三角形.
3.通过度量三角形的边长的实践活动,从
中理解三角形三边间的不等关系 教学难点 1.在具体的图形中不重复,且不遗漏地识
别所有三角形.
2.用三角形三边不等关系判定三条线段
可否组成三角形 教法学法分析教材学情分析教学目标过程设计重点难点教学评价教学方法 观察——实验——讨论的教学方法多媒体辅助教学动手实践——自主探索——合作交流
的学习方法学习方法
教法学法分析教材学情分析教学目标过程设计重点难点教学评价四、过程设计 创设情景
引入新知 埃菲尔铁塔雄居于法国首都巴黎市中心的战神较场上。它是法国政府为庆祝年法国资产阶级大革命一百周年、举办世界博览会建立起来的永久性纪念物。 生活中的三角形! 生活中有许多使用三角形的实例,
你会举出一些实例吗?畅所欲言 同学们,你们知道哪些和三角形
有关的知识?说来听听!请动手画一个三角形。
说说你是怎样画的。快画一画吧!
观察下列图形:三角形的定义:四、过程设计 创设情景
引入新知自主学习
知识探究1、三角形ABC用符号表示( )
2、三角形有几个顶点?有几个内角?有几条边?
3、三角形ABC的边AB、AC、和BC可用小写字母分别表示为( )自学课本 70页第一部分至思考 ,回答以下问题:ABCabc记作: ABC三角形的顶点: A、B、C三角形的边:AB、AC、BC三角形的内角: A、 B、 Ccba我要和三角形交朋友智力大冲浪1.图中共有 个三角形,它们分别是 :
__________________________小结: 数三角形的个数时,抓住不在同一条直线上的三个
点能组成一个三角形;再按字母的顺序去数。2.以AB为边的三角形有哪些?3.以E为顶点的三角形有哪些?4.以∠D为角的三角形有哪些?智力大冲浪ABCDE 5.△BCD的三边分别是:
__________
三个角分别是:
_________
三个顶点分别是:
________
其中顶点C的对边是:_____________
∠D是由_____和______两边组成的内角
∠BEC是△BCD的内角吗?智力大冲浪思考:回想一下三角形按角可以分几类?按边呢?三角形的分类三角形四、过程设计 自主学习
知识探究小组试验
验证猜想创设情景
引入新知争鸣乐园谈谈你的想法两条路线长分别是BC,AB+AC.由“两点之间,线段最短”
可以得到AB+AC>BC 如图三角形中,假设有一只“难得糊涂”的小虫
要从点B出发沿着三角形的边爬到点C,它有几条
路线可以选择?各条路线的长一样吗?同理可得:AC+BC>AB,AB+BC>AC路线1:由点B到点C路线2:由点B到点A,再由点A到点C。三角形的三边有这样的关系:
三角形两边的和大于第三边结论实践质疑园(动动手,动动脑,小组合作交流一) 选择7cm、8cm、9cm、16cm的小棒摆一摆,三根一组,共有几种
组合,其中哪些组合不能构成三角形?哪些组合能构成三角形? 不能组成三角形的组合____________________________ 能组成三角形的组合___________________________ 是不是任意三条线段都能组成一个三角形? 通过试验,思考下面的问题:三角形的两边之和大于第三边。 三角形的三边关系:实践质疑园(动动手,动动脑,小组合作交流二) (1)根据你画的三角形,量出它的三边长度,并填空:
a=______;b=_______;c=______(2)计算并验证:
a+b>c; b+c>a; c+a>b
(3)计算并比较:
a-b____c; b-c____a; c-a____b
(4)通过以上的计算你认为一个三角形中任意两边之差与第三边的长度有怎样的关系?三角形的任意两边之差,小于第三边四、过程设计 自主学习
知识探究小组试验
验证猜想创设情景
引入新知反馈训练
应用知识 (1)基础练习 下列长度的三条线段能否组成三角形?为什么?(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 2 : 3 : 4 ( )
(4) 3,5,8 ( )应用新知,体验成功小窍门:比较较短的两边之和与最长边的大小即可。试一试,相信自己 学校的木工师傅现有两根木条,木条长分
别70厘米和100厘米,他要选择第三根木条,
将它们钉成一个三角形木架,你能帮助确定
第三条边最长是多少厘米?最短是多少厘米
吗? (2) 拓展练习已知三角形两边的长度,第三边长度范围是:两边之差的绝对值<第三边<两边之和。如果告诉你:
三角形两边的长度,
第三边长度的范围你能确定吗?小窍门请你来帮忙 金老师想制作一个三角形木架,现有两根长度为19cm和9cm的木棒,第三根的长度X的取值范围是多少?(3)变式练习 金老师想制作一个三角形木架,现有两根长度为19cm和9cm的木棒,如果要求第三根木棒的长度是偶数,我有几种选法?第三根的长度可以是多少?变式一: 金老师想制作一个三角形木架,现有两根长度为19cm和9cm的木棒,如果要求第三根木棒的长度是奇数,我有几种选法?第三根的长度可以是多少?变式二: 金老师想制作一个等腰三角形木架,现有两根长度为19cm和10cm的木棒,我有几种选法?第三根的长度可以是多少?三角形的周长是多少?变式三: 金老师想制作一个等腰三角形木架,现有两根长度为19cm和8cm的木棒,我有几种选法?第三根的长度可以是多少?三角形的周长是多少?变式四:麦田某村庄和小学分别位于两条交叉的大路边(如图)。可是,每年冬天麦田弄不好就会走出一条小路来。你能不能运用今天所学的知识解释这一现象。这样走对吗?(4)应用练习小论坛答:不相信。如果他一步能走4米,由三角形三边的关系得,他两腿长的和得大于4米,这与实际情况相矛盾,所以他一步不能走4米。 有人说他一步能走4米, 你相信吗?归纳小结1.你在本节课中最大的收获是什么?
2.说说你在本节课中最喜欢的是什么?
作业 1. P75 2,6
2.设计一张由三角形为基本图 形构成的美丽图案。板书设计课题:7.1三角形的边
1、三角形的定义2、三角形三边之间的不等关系 谢 谢!
多提宝贵意见!
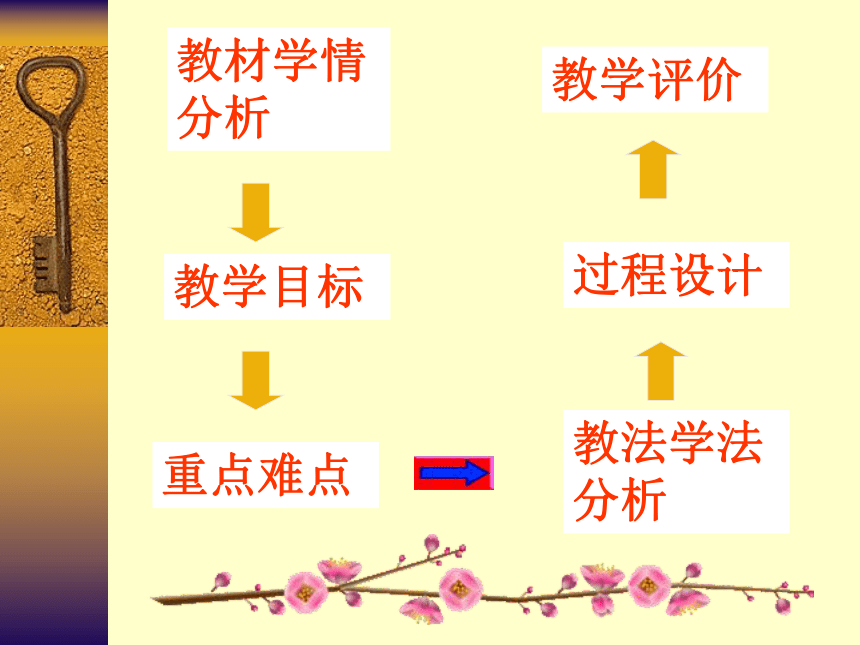
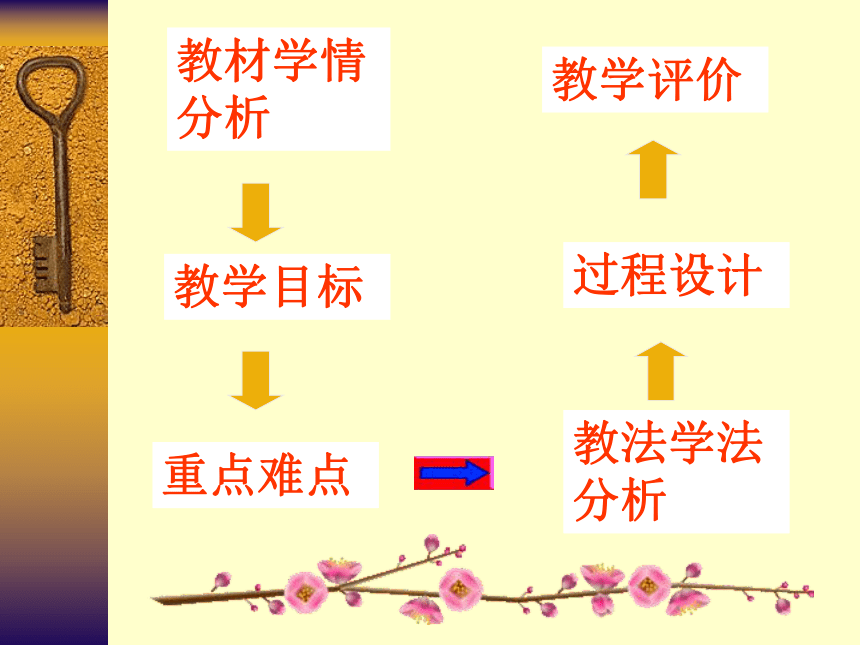
(说 课) 人教版七年级数学下册§7.1教法学法分析教材学情分析教学目标过程设计重点难点教学评价一、教材分析及学情分析1、教材的地位与作用2、学情分析 本节课是七年级下第七章的第一节,学生在小
学已学过一些三角形的知识,在前面学过线段、
角以及相交线、平行线等知识。他们的空间观念
得到进一步的发展,这样再来学习三角形的有关
内容,就有了更为充实的基础和准备。通过本节
的学习,可以丰富和加深学生对三角形边的认识。
同时为学习三角形的其他知识打好基础。起到了
承上启下的作用。教材分析一、教材分析及学情分析1、教材的地位与作用2、学情分析学情分析 在正式学习三角形三边关系之前,学生在生活
中已经积累了很多关于三角形三边关系的感性经验,
这些经验构成了学生学习的认知基础。教学过程中,
学生在抽象概括三角形三边之间的关系时,可能在
数学语言的描述上会有一定的困难,表达上也可能
不够严密,但只要学生表达的意思对,教师就应该
积极的给以肯定,同时教师要给学生更多探讨的空
间和交流的机会,毕竟数学模型的建立和思维的发
展需要经历一个渐近思辩的过程。 教法学法分析教材学情分析教学目标过程设计重点难点教学评价1、知识与技能目标2、过程与方法目标3、情感、态度与价值观目标二、教学目标知识目标 认识三角形,了解三角形的意义,认识三角
形的边、内角、顶点,能用符号语言表示三
角形. 1.经历度量三角形边长的实践活动中,理解三角形三边不等的关系.
2.懂得判断三条线段可否构成一个三角形的方法,并能运用它解决有关的问题.能力目标情感目标 帮助学生树立几何知识源于客观实际,用客观
实际的观念,激发学生学习的兴趣.教法学法分析教材学情分析教学目标过程设计重点难点教学评价教学重点 1.对三角形有关概念的了解,能用符号语
言表示三条形.
2.能从图中识别三角形.
3.通过度量三角形的边长的实践活动,从
中理解三角形三边间的不等关系 教学难点 1.在具体的图形中不重复,且不遗漏地识
别所有三角形.
2.用三角形三边不等关系判定三条线段
可否组成三角形 教法学法分析教材学情分析教学目标过程设计重点难点教学评价教学方法 观察——实验——讨论的教学方法多媒体辅助教学动手实践——自主探索——合作交流
的学习方法学习方法
教法学法分析教材学情分析教学目标过程设计重点难点教学评价四、过程设计 创设情景
引入新知 埃菲尔铁塔雄居于法国首都巴黎市中心的战神较场上。它是法国政府为庆祝年法国资产阶级大革命一百周年、举办世界博览会建立起来的永久性纪念物。 生活中的三角形! 生活中有许多使用三角形的实例,
你会举出一些实例吗?畅所欲言 同学们,你们知道哪些和三角形
有关的知识?说来听听!请动手画一个三角形。
说说你是怎样画的。快画一画吧!
观察下列图形:三角形的定义:四、过程设计 创设情景
引入新知自主学习
知识探究1、三角形ABC用符号表示( )
2、三角形有几个顶点?有几个内角?有几条边?
3、三角形ABC的边AB、AC、和BC可用小写字母分别表示为( )自学课本 70页第一部分至思考 ,回答以下问题:ABCabc记作: ABC三角形的顶点: A、B、C三角形的边:AB、AC、BC三角形的内角: A、 B、 Ccba我要和三角形交朋友智力大冲浪1.图中共有 个三角形,它们分别是 :
__________________________小结: 数三角形的个数时,抓住不在同一条直线上的三个
点能组成一个三角形;再按字母的顺序去数。2.以AB为边的三角形有哪些?3.以E为顶点的三角形有哪些?4.以∠D为角的三角形有哪些?智力大冲浪ABCDE 5.△BCD的三边分别是:
__________
三个角分别是:
_________
三个顶点分别是:
________
其中顶点C的对边是:_____________
∠D是由_____和______两边组成的内角
∠BEC是△BCD的内角吗?智力大冲浪思考:回想一下三角形按角可以分几类?按边呢?三角形的分类三角形四、过程设计 自主学习
知识探究小组试验
验证猜想创设情景
引入新知争鸣乐园谈谈你的想法两条路线长分别是BC,AB+AC.由“两点之间,线段最短”
可以得到AB+AC>BC 如图三角形中,假设有一只“难得糊涂”的小虫
要从点B出发沿着三角形的边爬到点C,它有几条
路线可以选择?各条路线的长一样吗?同理可得:AC+BC>AB,AB+BC>AC路线1:由点B到点C路线2:由点B到点A,再由点A到点C。三角形的三边有这样的关系:
三角形两边的和大于第三边结论实践质疑园(动动手,动动脑,小组合作交流一) 选择7cm、8cm、9cm、16cm的小棒摆一摆,三根一组,共有几种
组合,其中哪些组合不能构成三角形?哪些组合能构成三角形? 不能组成三角形的组合____________________________ 能组成三角形的组合___________________________ 是不是任意三条线段都能组成一个三角形? 通过试验,思考下面的问题:三角形的两边之和大于第三边。 三角形的三边关系:实践质疑园(动动手,动动脑,小组合作交流二) (1)根据你画的三角形,量出它的三边长度,并填空:
a=______;b=_______;c=______(2)计算并验证:
a+b>c; b+c>a; c+a>b
(3)计算并比较:
a-b____c; b-c____a; c-a____b
(4)通过以上的计算你认为一个三角形中任意两边之差与第三边的长度有怎样的关系?三角形的任意两边之差,小于第三边四、过程设计 自主学习
知识探究小组试验
验证猜想创设情景
引入新知反馈训练
应用知识 (1)基础练习 下列长度的三条线段能否组成三角形?为什么?(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 2 : 3 : 4 ( )
(4) 3,5,8 ( )应用新知,体验成功小窍门:比较较短的两边之和与最长边的大小即可。试一试,相信自己 学校的木工师傅现有两根木条,木条长分
别70厘米和100厘米,他要选择第三根木条,
将它们钉成一个三角形木架,你能帮助确定
第三条边最长是多少厘米?最短是多少厘米
吗? (2) 拓展练习已知三角形两边的长度,第三边长度范围是:两边之差的绝对值<第三边<两边之和。如果告诉你:
三角形两边的长度,
第三边长度的范围你能确定吗?小窍门请你来帮忙 金老师想制作一个三角形木架,现有两根长度为19cm和9cm的木棒,第三根的长度X的取值范围是多少?(3)变式练习 金老师想制作一个三角形木架,现有两根长度为19cm和9cm的木棒,如果要求第三根木棒的长度是偶数,我有几种选法?第三根的长度可以是多少?变式一: 金老师想制作一个三角形木架,现有两根长度为19cm和9cm的木棒,如果要求第三根木棒的长度是奇数,我有几种选法?第三根的长度可以是多少?变式二: 金老师想制作一个等腰三角形木架,现有两根长度为19cm和10cm的木棒,我有几种选法?第三根的长度可以是多少?三角形的周长是多少?变式三: 金老师想制作一个等腰三角形木架,现有两根长度为19cm和8cm的木棒,我有几种选法?第三根的长度可以是多少?三角形的周长是多少?变式四:麦田某村庄和小学分别位于两条交叉的大路边(如图)。可是,每年冬天麦田弄不好就会走出一条小路来。你能不能运用今天所学的知识解释这一现象。这样走对吗?(4)应用练习小论坛答:不相信。如果他一步能走4米,由三角形三边的关系得,他两腿长的和得大于4米,这与实际情况相矛盾,所以他一步不能走4米。 有人说他一步能走4米, 你相信吗?归纳小结1.你在本节课中最大的收获是什么?
2.说说你在本节课中最喜欢的是什么?
作业 1. P75 2,6
2.设计一张由三角形为基本图 形构成的美丽图案。板书设计课题:7.1三角形的边
1、三角形的定义2、三角形三边之间的不等关系 谢 谢!
多提宝贵意见!
