11.2.1 三角形的内角 课件(共23页PPT)2023-2024学年人教版八年级数学上册
文档属性
| 名称 | 11.2.1 三角形的内角 课件(共23页PPT)2023-2024学年人教版八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 623.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-04 00:00:00 | ||
图片预览


文档简介
(共23张PPT)
人教版八年级数学上册
11.2.1 三角形的内角
学习目标
(1).探索并掌握三角形内角和定理
(2).会用三角形内角和进行角度的计算
(3).能证明三角形的内角和定理及其推论
(4).能运用三角形的内角和定理及其推论判断角和边的关系,解决简单的实际问题。
重点
三角形的内角
难点
先天下之忧而忧,后天下之乐而乐
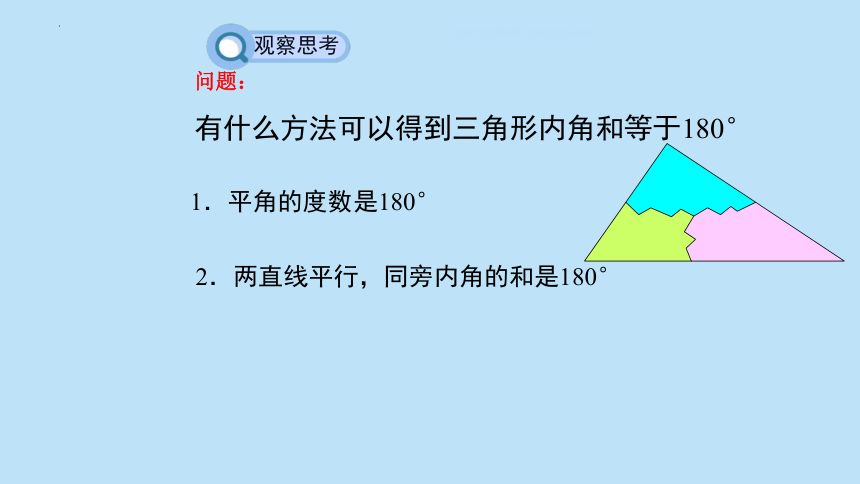
问题:
有什么方法可以得到三角形内角和等于180°
观察思考
1.平角的度数是180°
2.两直线平行,同旁内角的和是180°
先天下之忧而忧,后天下之乐而乐
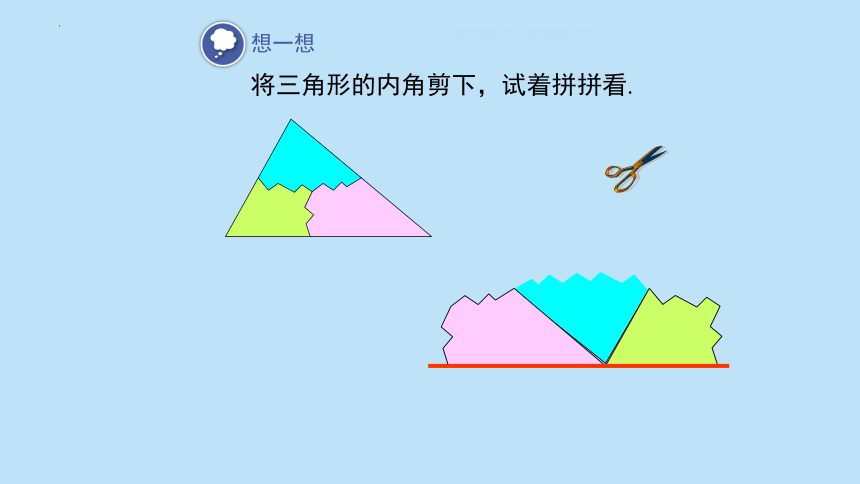
将三角形的内角剪下,试着拼拼看.
想一想
先天下之忧而忧,后天下之乐而乐
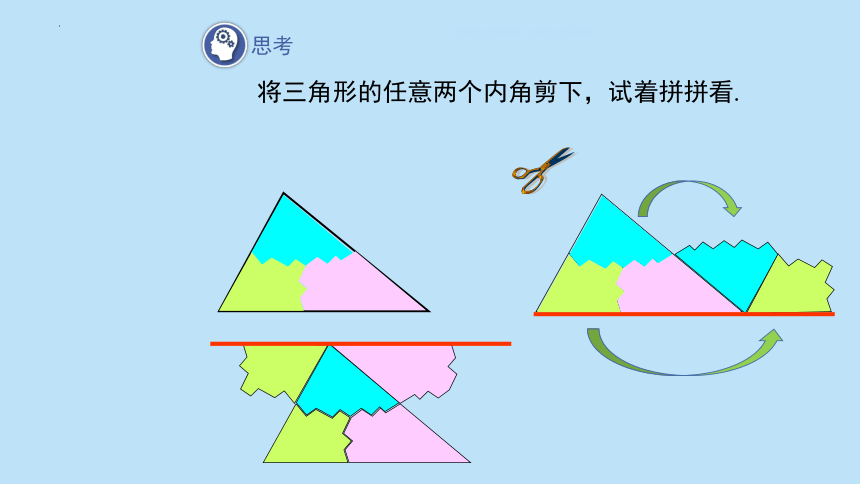
思考
将三角形的任意两个内角剪下,试着拼拼看.
先天下之忧而忧,后天下之乐而乐
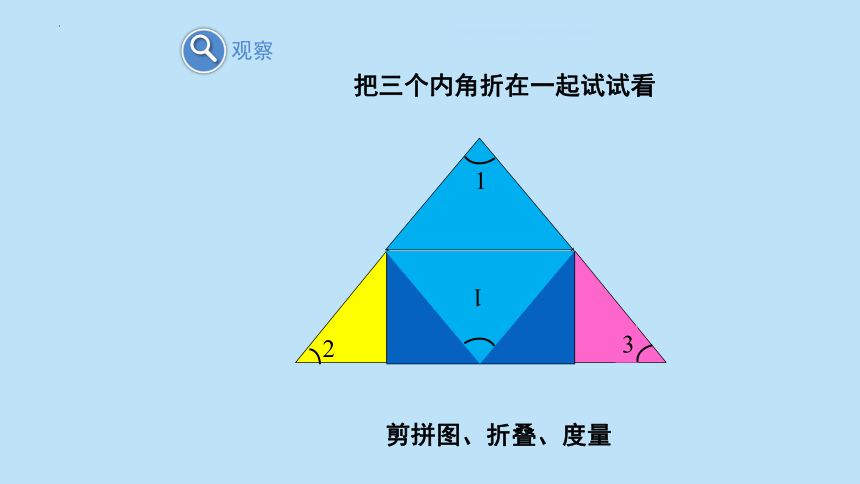
把三个内角折在一起试试看
1
2
2
3
3
剪拼图、折叠、度量
1
观察
先天下之忧而忧,后天下之乐而乐
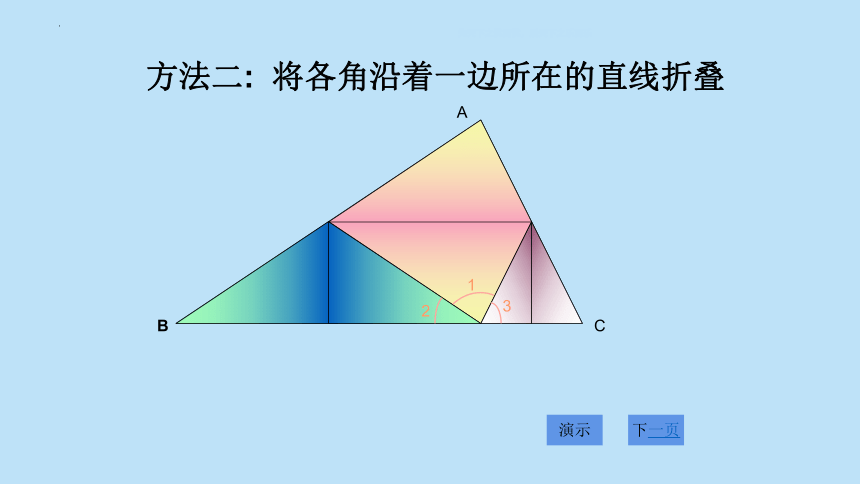
A
B
C
演示
下一页
1
2
3
方法二: 将各角沿着一边所在的直线折叠
先天下之忧而忧,后天下之乐而乐
如果△ABC是画在一块不能分割的平面上,如在黑板上,这时就不可能做到把∠A、∠B撕下来再分别放在∠1、∠2的位置上,那么又如何论证∠A+∠B+∠C= 180゜呢?
先天下之忧而忧,后天下之乐而乐
2
1
F
D
C
B
A
三角形的内角和等于1800.
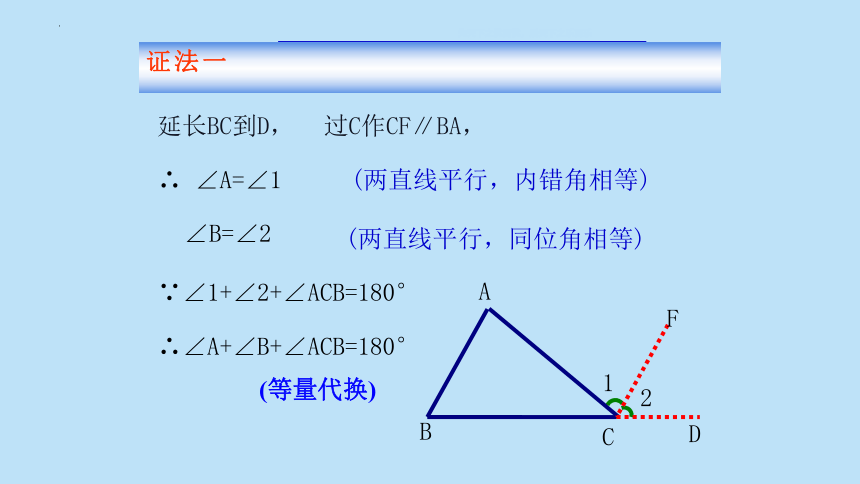
延长BC到D,
过C作CF∥BA,
∴ ∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
(两直线平行,同位角相等)
∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
证法一
(等量代换)
先天下之忧而忧,后天下之乐而乐
F
2
1
E
C
B
A
三角形的内角和等于1800.
过A作EF∥BC,
∴∠B=∠2
(两直线平行,内错角相等)
∠C=∠1
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°
∴∠B+∠C+∠BAC=180°
证法二
(等量代换)
先天下之忧而忧,后天下之乐而乐
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。
为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
思路总结
先天下之忧而忧,后天下之乐而乐
三角形内角和定理:
三角形的内角和等于1800.
几何语言:
在△ABC中, ∠A +∠B +∠C=180 °
先天下之忧而忧,后天下之乐而乐
通过刚才具体的度量和拼剪,确实可以验证出三角形的内角和为180°,但由于测量和拼剪会有误差,这些验证不是数学证明,不能完全的让人信服,下面我们用推理论证的方法去证明.
先天下之忧而忧,后天下之乐而乐
证一证
活动:
先天下之忧而忧,后天下之乐而乐
A
B
C
已知:△A B C, 求证:∠A +∠B +∠C =180°
D
E
证明:过点A作DE∥BC
∠C =∠EAC
(等量代换)
∴∠B =∠DAB
(两直线平行,内错角相等)
又∵∠DAB+∠BAC+∠EAC=180°
∴∠B+∠C+∠BAC=180°
先天下之忧而忧,后天下之乐而乐
探究新知
已知:△ABC, 求证:∠A +∠B +∠C =180°
A
B
C
D
E
过点C作CD∥BA.
证明:延长BC到点E,
∴ ∠A = ∠ACD
∠B=∠DCE
(两直线平行,内错角相等)
(两直线平行,同位角相等)
又∵∠BCA+∠ACD+∠DCE=180°
∴∠A+∠B+∠ACB=180°
(等量代换)
先天下之忧而忧,后天下之乐而乐
添加辅助线思路
)
2
)
1
2
1
1.构造平角
三角形内角和定理: 三角形的内角和等于180°.
A
B
C
E
2.构造同旁内角
转化思想
先天下之忧而忧,后天下之乐而乐
如图,在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线,求∠ADB的度数
随堂练习
解:∵∠BAC=40°,
AD是△ABC的角平分线,
∴∠BAD=BAC=20°
在△ABD中,
∠ADB=180°-∠B-∠BAD
=180°-75°-20°=85°
先天下之忧而忧,后天下之乐而乐
随堂练习
直角三角形的两个锐角互余.
A
B
C
先天下之忧而忧,后天下之乐而乐
随堂练习
直角三角形可以用符号“Rt△”表示,
直角三角形ABC 可以写成Rt△ABC .
A
B
C
先天下之忧而忧,后天下之乐而乐
82°
80 °
60 °
40 °
C
(1)如图,在△ABC中,∠A=55°,∠B=43 °
则∠ACB = ∠ACD = .
(2)如图,∠A+∠B+ ∠C+∠D+∠E+∠F= .
(1) (2)
(3)在△ABC中,∠A :∠B:∠C=2:3:4
则∠A = ∠ B= ∠ C= .
B
A
D
98°
A
B
C
D
E
F
360°
巩固练习
先天下之忧而忧,后天下之乐而乐
解:在△RtACD中∠CAD =30 °∠D =90 °
D
A
B
C
∴ ∠ACD =180 ° -30 ° -90 °=6 0 °
在Rt△BCD中 ∠CBD = 45 ° ∠D =90 °
∴ ∠BCD = 180 °- 90°-45 °=45 °
∴ ∠ACB = ∠ACD - ∠BCD = 6 0 °- 45 °=15°
1、如图,从A处观测C处时仰角∠CAD=30°,从B处观测C处时仰角∠CBD=45°.从C处观测A、B两处时视角∠ACB是多少
应用创新
先天下之忧而忧,后天下之乐而乐
1、三角形的内角和定理:
三角形三个内角之和为180°
2、由三角形内角和等于180°,可得出
(1)直角三角形的两个锐角互余;
(2)有两个角互余的三角形是直角三角形
(3)一个三角形最多有一个直角或钝角;
(4)任意一个三角形中,最多有三个锐角,
最少有两个锐角;
(5)一个三角形中至少有一个角小于或等于60°
课堂小结
人教版八年级数学上册
11.2.1 三角形的内角
学习目标
(1).探索并掌握三角形内角和定理
(2).会用三角形内角和进行角度的计算
(3).能证明三角形的内角和定理及其推论
(4).能运用三角形的内角和定理及其推论判断角和边的关系,解决简单的实际问题。
重点
三角形的内角
难点
先天下之忧而忧,后天下之乐而乐
问题:
有什么方法可以得到三角形内角和等于180°
观察思考
1.平角的度数是180°
2.两直线平行,同旁内角的和是180°
先天下之忧而忧,后天下之乐而乐
将三角形的内角剪下,试着拼拼看.
想一想
先天下之忧而忧,后天下之乐而乐
思考
将三角形的任意两个内角剪下,试着拼拼看.
先天下之忧而忧,后天下之乐而乐
把三个内角折在一起试试看
1
2
2
3
3
剪拼图、折叠、度量
1
观察
先天下之忧而忧,后天下之乐而乐
A
B
C
演示
下一页
1
2
3
方法二: 将各角沿着一边所在的直线折叠
先天下之忧而忧,后天下之乐而乐
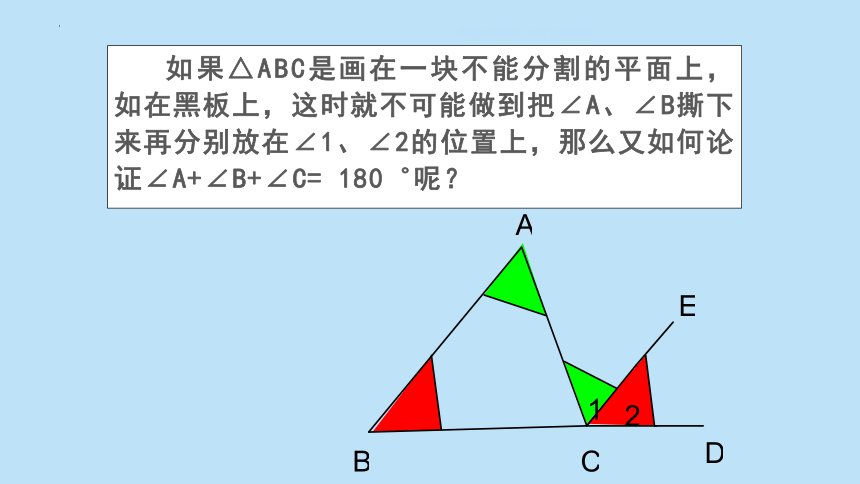
如果△ABC是画在一块不能分割的平面上,如在黑板上,这时就不可能做到把∠A、∠B撕下来再分别放在∠1、∠2的位置上,那么又如何论证∠A+∠B+∠C= 180゜呢?
先天下之忧而忧,后天下之乐而乐
2
1
F
D
C
B
A
三角形的内角和等于1800.
延长BC到D,
过C作CF∥BA,
∴ ∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
(两直线平行,同位角相等)
∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
证法一
(等量代换)
先天下之忧而忧,后天下之乐而乐
F
2
1
E
C
B
A
三角形的内角和等于1800.
过A作EF∥BC,
∴∠B=∠2
(两直线平行,内错角相等)
∠C=∠1
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°
∴∠B+∠C+∠BAC=180°
证法二
(等量代换)
先天下之忧而忧,后天下之乐而乐
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。
为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
思路总结
先天下之忧而忧,后天下之乐而乐
三角形内角和定理:
三角形的内角和等于1800.
几何语言:
在△ABC中, ∠A +∠B +∠C=180 °
先天下之忧而忧,后天下之乐而乐
通过刚才具体的度量和拼剪,确实可以验证出三角形的内角和为180°,但由于测量和拼剪会有误差,这些验证不是数学证明,不能完全的让人信服,下面我们用推理论证的方法去证明.
先天下之忧而忧,后天下之乐而乐
证一证
活动:
先天下之忧而忧,后天下之乐而乐
A
B
C
已知:△A B C, 求证:∠A +∠B +∠C =180°
D
E
证明:过点A作DE∥BC
∠C =∠EAC
(等量代换)
∴∠B =∠DAB
(两直线平行,内错角相等)
又∵∠DAB+∠BAC+∠EAC=180°
∴∠B+∠C+∠BAC=180°
先天下之忧而忧,后天下之乐而乐
探究新知
已知:△ABC, 求证:∠A +∠B +∠C =180°
A
B
C
D
E
过点C作CD∥BA.
证明:延长BC到点E,
∴ ∠A = ∠ACD
∠B=∠DCE
(两直线平行,内错角相等)
(两直线平行,同位角相等)
又∵∠BCA+∠ACD+∠DCE=180°
∴∠A+∠B+∠ACB=180°
(等量代换)
先天下之忧而忧,后天下之乐而乐
添加辅助线思路
)
2
)
1
2
1
1.构造平角
三角形内角和定理: 三角形的内角和等于180°.
A
B
C
E
2.构造同旁内角
转化思想
先天下之忧而忧,后天下之乐而乐
如图,在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线,求∠ADB的度数
随堂练习
解:∵∠BAC=40°,
AD是△ABC的角平分线,
∴∠BAD=BAC=20°
在△ABD中,
∠ADB=180°-∠B-∠BAD
=180°-75°-20°=85°
先天下之忧而忧,后天下之乐而乐
随堂练习
直角三角形的两个锐角互余.
A
B
C
先天下之忧而忧,后天下之乐而乐
随堂练习
直角三角形可以用符号“Rt△”表示,
直角三角形ABC 可以写成Rt△ABC .
A
B
C
先天下之忧而忧,后天下之乐而乐
82°
80 °
60 °
40 °
C
(1)如图,在△ABC中,∠A=55°,∠B=43 °
则∠ACB = ∠ACD = .
(2)如图,∠A+∠B+ ∠C+∠D+∠E+∠F= .
(1) (2)
(3)在△ABC中,∠A :∠B:∠C=2:3:4
则∠A = ∠ B= ∠ C= .
B
A
D
98°
A
B
C
D
E
F
360°
巩固练习
先天下之忧而忧,后天下之乐而乐
解:在△RtACD中∠CAD =30 °∠D =90 °
D
A
B
C
∴ ∠ACD =180 ° -30 ° -90 °=6 0 °
在Rt△BCD中 ∠CBD = 45 ° ∠D =90 °
∴ ∠BCD = 180 °- 90°-45 °=45 °
∴ ∠ACB = ∠ACD - ∠BCD = 6 0 °- 45 °=15°
1、如图,从A处观测C处时仰角∠CAD=30°,从B处观测C处时仰角∠CBD=45°.从C处观测A、B两处时视角∠ACB是多少
应用创新
先天下之忧而忧,后天下之乐而乐
1、三角形的内角和定理:
三角形三个内角之和为180°
2、由三角形内角和等于180°,可得出
(1)直角三角形的两个锐角互余;
(2)有两个角互余的三角形是直角三角形
(3)一个三角形最多有一个直角或钝角;
(4)任意一个三角形中,最多有三个锐角,
最少有两个锐角;
(5)一个三角形中至少有一个角小于或等于60°
课堂小结
