19.2菱形 说课课件[下学期]
文档属性
| 名称 | 19.2菱形 说课课件[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-09 18:49:00 | ||
图片预览








文档简介
(共23张PPT)
教材分析:
《菱形》这节课是人教版八年级下册第十九章第二节的内容,它是一个特殊的平行四边形,也是学习正方形的基础,在本章中起承上启下的作用。而学生已经学习了矩形的内容,所以对于菱形定义的学习不会感到十分困难。
教学目标:
1、让学生掌握菱形概念,知道菱形与平行四边形的关系。 2、掌握菱形的性质,体会菱形的图形美。 3、能运用菱形知识解决具体问题,提高分析能力和观察能力,培养学生的学习兴趣
1、教学重点: 菱形的性质定理。
2、教学难点:把菱形的性质和直角三角形的知识综合运用。
教学方法:
教师作引导,学生为主体,以学生的互动学习为主,通过实验,提高学生的分析能力 ,在合作、交流的气氛下进行师生互动,培养学生的自学能力和创新意识。
教学过程:
一、复习回顾
二、课题引入
三、课题教学
四、小结
五、作业
(1)平行四边形有哪些性质 矩形与平行四边形比较有哪些特殊的性质
平行四边形
边:
角:
对角线:
对边平行且相等
对角相等邻角互补
对角线互相平分
矩形
角:
四个角是直角
对角线:
对角线相等
上图中有你熟悉的图形吗?
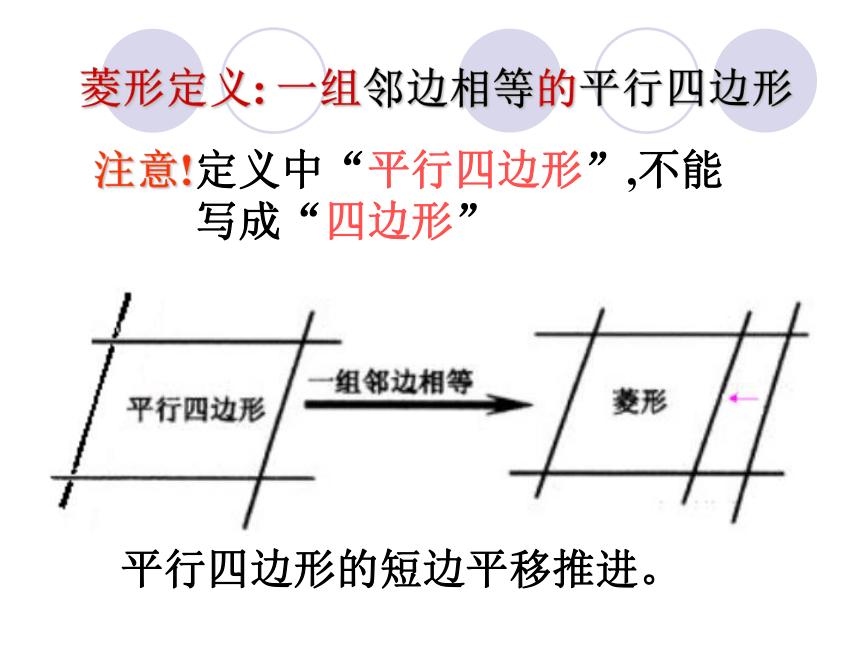
平行四边形的短边平移推进。
菱形定义:
一组邻边相等的平行四边形
注意!
定义中“平行四边形”,不能
写成“四边形”
判断题
1、有一组邻边相等的四边形是菱形。( )
2、菱形是平行四边形。( )
3、平行四边形是菱形。( )
做
一
做
将一张矩形纸对折两次,沿虚线剪下一个角,打开后,这是一个什么样的图形
菱形除了具有平行四边形一切性质外,它还有什么特殊性质
菱形
边:
四条边相等
对角线:
互相垂直
分别平分两组对角
轴对称图形
A
B
C
D
在菱形ABCD中,已知∠ABC=120°
则: 1) ∠ABD= ______
2)∠DAO= ___
试一试
B
A
C
D
O
60 °
30 °
这些性质你掌握好了吗 下面我来考考你!
1.判断题
(1)有一条对角线平分一组对角的四边形
是菱形 ( )
(2)菱形的对角线互相垂直平分,且平分各内角.( )
(3)菱形是轴对称图形,它的对称轴只有一条( )
错
对
错
如图:菱形花坛ABCD的边长为20m,∠ABC=600,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(分别精确到0.01m和0.1m2)。
O
C
B
A
D
解:∵花坛ABCD是菱形,
∴AC⊥BD,∠ABO= ∠ABC= ×60°=30°
在Rt△OAB中,AO= AB= ×20=10(m),
BO= = ≈17.32(m),
∴花坛的两条小路长
AC=2AO=20(M) BD=2BO≈34.64(M).
花坛的面积: S菱形ABCD=4S△OAB= AC×BD≈346.4(M 2).
练一练:
1、四边形ABCD是菱形,O是两条对角线的交点。已知AB=5cm,AO=4cm,求对角线AC和BD的长。
O
D
C
B
A
菱形的性质
菱形的性质
边:
四条边相等
对角线:
互相垂直
分别平分两组对角
轴对称图形
具有平行四边形一切性质
课本P113 5、P114 12
让我们课后做一做!
评价分析:
这节课是菱形的第1课时,主要内容是菱形的定义和性质。为了体现新课标的要求,在菱形的性质的教学形式上,采用了数学活动的方法。让学生动手实验,通过观察发现,自己讨论、探究、交流,总结出本节课的重点——菱形的性质。这样,学生自己得出的猜想和证明会更让他们易于接受,而解题方法也在此过程中也渗透给学生。为学生提供思维发展、合作交流的空间。激发学生学习数学的兴趣。
而练习的设计,重在加深学生对相关内容的认识,培养学生的合作性。提高学生的解题能力,扩大 学生的知识面,拓展思维。
教材分析:
《菱形》这节课是人教版八年级下册第十九章第二节的内容,它是一个特殊的平行四边形,也是学习正方形的基础,在本章中起承上启下的作用。而学生已经学习了矩形的内容,所以对于菱形定义的学习不会感到十分困难。
教学目标:
1、让学生掌握菱形概念,知道菱形与平行四边形的关系。 2、掌握菱形的性质,体会菱形的图形美。 3、能运用菱形知识解决具体问题,提高分析能力和观察能力,培养学生的学习兴趣
1、教学重点: 菱形的性质定理。
2、教学难点:把菱形的性质和直角三角形的知识综合运用。
教学方法:
教师作引导,学生为主体,以学生的互动学习为主,通过实验,提高学生的分析能力 ,在合作、交流的气氛下进行师生互动,培养学生的自学能力和创新意识。
教学过程:
一、复习回顾
二、课题引入
三、课题教学
四、小结
五、作业
(1)平行四边形有哪些性质 矩形与平行四边形比较有哪些特殊的性质
平行四边形
边:
角:
对角线:
对边平行且相等
对角相等邻角互补
对角线互相平分
矩形
角:
四个角是直角
对角线:
对角线相等
上图中有你熟悉的图形吗?
平行四边形的短边平移推进。
菱形定义:
一组邻边相等的平行四边形
注意!
定义中“平行四边形”,不能
写成“四边形”
判断题
1、有一组邻边相等的四边形是菱形。( )
2、菱形是平行四边形。( )
3、平行四边形是菱形。( )
做
一
做
将一张矩形纸对折两次,沿虚线剪下一个角,打开后,这是一个什么样的图形
菱形除了具有平行四边形一切性质外,它还有什么特殊性质
菱形
边:
四条边相等
对角线:
互相垂直
分别平分两组对角
轴对称图形
A
B
C
D
在菱形ABCD中,已知∠ABC=120°
则: 1) ∠ABD= ______
2)∠DAO= ___
试一试
B
A
C
D
O
60 °
30 °
这些性质你掌握好了吗 下面我来考考你!
1.判断题
(1)有一条对角线平分一组对角的四边形
是菱形 ( )
(2)菱形的对角线互相垂直平分,且平分各内角.( )
(3)菱形是轴对称图形,它的对称轴只有一条( )
错
对
错
如图:菱形花坛ABCD的边长为20m,∠ABC=600,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(分别精确到0.01m和0.1m2)。
O
C
B
A
D
解:∵花坛ABCD是菱形,
∴AC⊥BD,∠ABO= ∠ABC= ×60°=30°
在Rt△OAB中,AO= AB= ×20=10(m),
BO= = ≈17.32(m),
∴花坛的两条小路长
AC=2AO=20(M) BD=2BO≈34.64(M).
花坛的面积: S菱形ABCD=4S△OAB= AC×BD≈346.4(M 2).
练一练:
1、四边形ABCD是菱形,O是两条对角线的交点。已知AB=5cm,AO=4cm,求对角线AC和BD的长。
O
D
C
B
A
菱形的性质
菱形的性质
边:
四条边相等
对角线:
互相垂直
分别平分两组对角
轴对称图形
具有平行四边形一切性质
课本P113 5、P114 12
让我们课后做一做!
评价分析:
这节课是菱形的第1课时,主要内容是菱形的定义和性质。为了体现新课标的要求,在菱形的性质的教学形式上,采用了数学活动的方法。让学生动手实验,通过观察发现,自己讨论、探究、交流,总结出本节课的重点——菱形的性质。这样,学生自己得出的猜想和证明会更让他们易于接受,而解题方法也在此过程中也渗透给学生。为学生提供思维发展、合作交流的空间。激发学生学习数学的兴趣。
而练习的设计,重在加深学生对相关内容的认识,培养学生的合作性。提高学生的解题能力,扩大 学生的知识面,拓展思维。
