第五单元 圆--扇形 同步练习 人教版数学 六年级上册(有答案)
文档属性
| 名称 | 第五单元 圆--扇形 同步练习 人教版数学 六年级上册(有答案) | 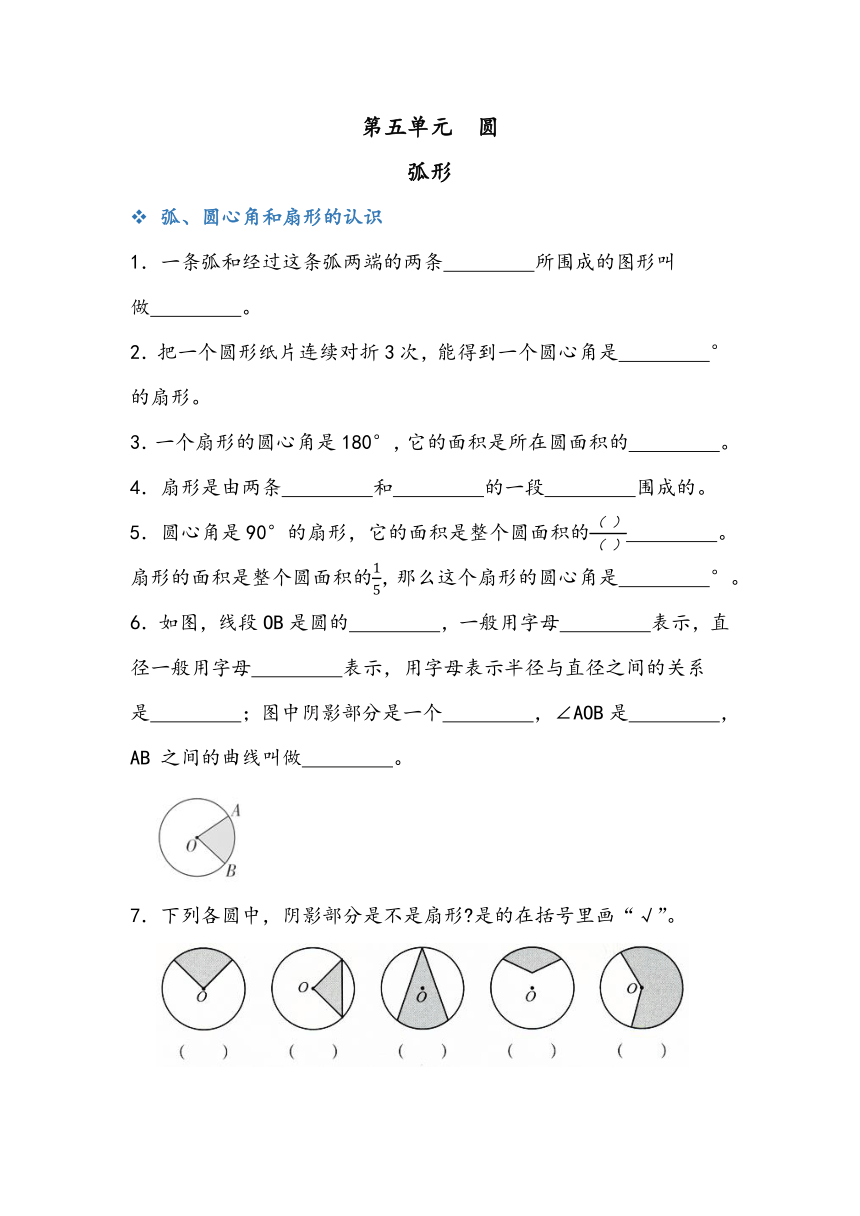 | |
| 格式 | docx | ||
| 文件大小 | 312.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-04 08:35:10 | ||
图片预览



文档简介
第五单元 圆
弧形
弧、圆心角和扇形的认识
1.一条弧和经过这条弧两端的两条 所围成的图形叫做 。
2.把一个圆形纸片连续对折3次,能得到一个圆心角是 °的扇形。
3.一个扇形的圆心角是180°,它的面积是所在圆面积的 。
4.扇形是由两条 和 的一段 围成的。
5.圆心角是90°的扇形,它的面积是整个圆面积的 。扇形的面积是整个圆面积的,那么这个扇形的圆心角是 °。
6.如图,线段OB是圆的 ,一般用字母 表示,直径一般用字母 表示,用字母表示半径与直径之间的关系是 ;图中阴影部分是一个 ,∠AOB是 ,AB 之间的曲线叫做 。
7.下列各圆中,阴影部分是不是扇形 是的在括号里画“√”。
8.已知圆的周长为25.12cm,在这个圆中的扇形AOB的面积为12.56cm2.
(1)圆心角∠AOB的度数;
(2) 的长.
9.给一把圆形的扇子镶边,共用去50.24厘米长的布条。这把扇子的面积是多少平方厘米?
扇形的面积
10.如下图所示,正方形面积是12cm2,那么圆空白部分的面积是
11.下图中,半圆的直径是4cm,求图中阴影部分的面积是 平方厘米。
12.一个圆里面有一个圆心角是60°的扇形,面积是18.84平方厘米,这个圆的面积是 平方厘米。
13.在下图的扇形中,点A、B为半径的中点,三角形AOB的面积为5cm2,那么阴影部分的面积为 cm2。
14.如图,点A,B,C均在圆上,把圆分别沿AB、BC对折,对折后,均过圆O的圆心O,则图中阴影部分面积和圆面积之比是 。
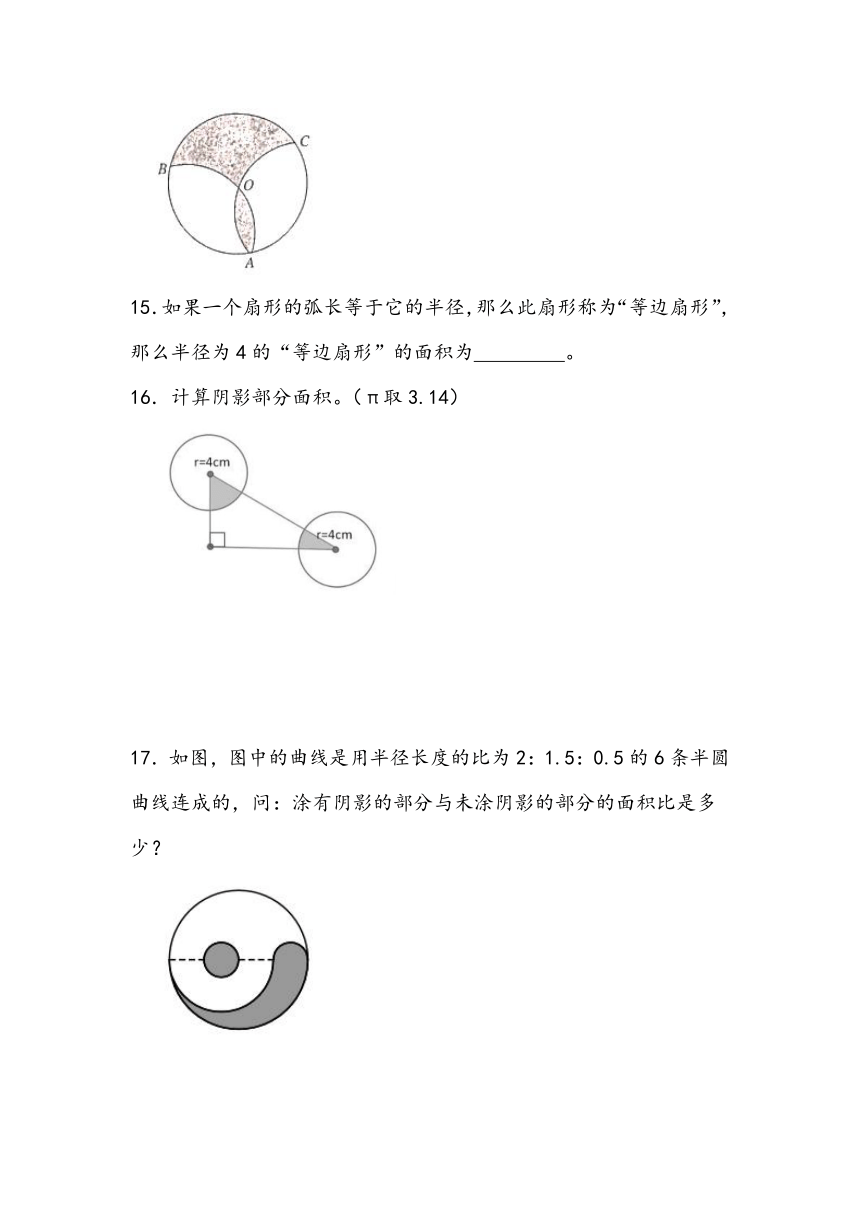
15.如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”,那么半径为4的“等边扇形”的面积为 。
16.计算阴影部分面积。(π取3.14)
17.如图,图中的曲线是用半径长度的比为2:1.5:0.5的6条半圆曲线连成的,问:涂有阴影的部分与未涂阴影的部分的面积比是多少?
18.如图所示,O为圆心,OACB为梯形,求阴影部分的周长与面积.(单位:cm)
19.如图所示,在等腰直角三角形ABC中,AC=4厘米,BC是半圆的直径,A为扇形ACD的圆心,求阴影部分的面积是多少平方厘米?
参考答案
1.【答案】半径;扇形
2.【答案】45
3.【答案】
4.【答案】半径;圆上;曲线
5.【答案】;72
6.【答案】半径;r;d;d=2r;扇形;圆心角;弧
7.【答案】
8.【答案】(1)解:.14×(25.12÷3.14÷2)2
=3.14×42
=3.14×16
=50.24(平方厘米)
360×
=360×
=90(度);
答:圆心角∠AOB的度数是90度。
(2)解:25.12×
=
=6.28(厘米);
答:弧AB长6.28厘米.
9.【答案】解:扇子的半径:50.24÷(2×3.14)=50.24÷6.28=8(厘米);扇子的面积:3.14×82=3.14×64=200.96(平方厘米);答:这把扇子的面积是200.96平方厘米。
10.【答案】28.26平方厘米
11.【答案】2.28
12.【答案】113.04
13.【答案】26.4
14.【答案】1:3
15.【答案】8
16.【答案】解:3.14×42÷4
=3.14×16÷4
=50.24÷4
=12.56(平方厘米)
17.【答案】解:令大、中、小半圆的半径分别为4、3、1。
阴影部分面积:S1=1×1×π××3+(4×4×π-3×3×π)
=π+π
=5π
空白部分面积:S2=4×4×π-5π
=11π
S1:S2=5π:11π=5:11
答:涂有阴影的部分与未涂阴影的部分的面积比是5:11。
18.【答案】解:3.14×4×2÷4+5+6
=12.56×2÷4+5+6
=25.12÷4+5+6
=6.28+5+6
=11.28+6
=17.28(cm)
(4+6)×4÷2-3.14×42÷4
=10×4÷2-3.14×16÷4
=40÷2-50.24÷4
=20-12.56
=7.44(cm2)
19.【答案】解:如图所示:
×3.14×42+×3.14×(4÷2)2-×4×4
=×3.14×16+×3.14×4-2×4
=3.14×2+3.14×2-8
=6.28+6.28-8
=12.56-8
=4.56(平方厘米)
弧形
弧、圆心角和扇形的认识
1.一条弧和经过这条弧两端的两条 所围成的图形叫做 。
2.把一个圆形纸片连续对折3次,能得到一个圆心角是 °的扇形。
3.一个扇形的圆心角是180°,它的面积是所在圆面积的 。
4.扇形是由两条 和 的一段 围成的。
5.圆心角是90°的扇形,它的面积是整个圆面积的 。扇形的面积是整个圆面积的,那么这个扇形的圆心角是 °。
6.如图,线段OB是圆的 ,一般用字母 表示,直径一般用字母 表示,用字母表示半径与直径之间的关系是 ;图中阴影部分是一个 ,∠AOB是 ,AB 之间的曲线叫做 。
7.下列各圆中,阴影部分是不是扇形 是的在括号里画“√”。
8.已知圆的周长为25.12cm,在这个圆中的扇形AOB的面积为12.56cm2.
(1)圆心角∠AOB的度数;
(2) 的长.
9.给一把圆形的扇子镶边,共用去50.24厘米长的布条。这把扇子的面积是多少平方厘米?
扇形的面积
10.如下图所示,正方形面积是12cm2,那么圆空白部分的面积是
11.下图中,半圆的直径是4cm,求图中阴影部分的面积是 平方厘米。
12.一个圆里面有一个圆心角是60°的扇形,面积是18.84平方厘米,这个圆的面积是 平方厘米。
13.在下图的扇形中,点A、B为半径的中点,三角形AOB的面积为5cm2,那么阴影部分的面积为 cm2。
14.如图,点A,B,C均在圆上,把圆分别沿AB、BC对折,对折后,均过圆O的圆心O,则图中阴影部分面积和圆面积之比是 。
15.如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”,那么半径为4的“等边扇形”的面积为 。
16.计算阴影部分面积。(π取3.14)
17.如图,图中的曲线是用半径长度的比为2:1.5:0.5的6条半圆曲线连成的,问:涂有阴影的部分与未涂阴影的部分的面积比是多少?
18.如图所示,O为圆心,OACB为梯形,求阴影部分的周长与面积.(单位:cm)
19.如图所示,在等腰直角三角形ABC中,AC=4厘米,BC是半圆的直径,A为扇形ACD的圆心,求阴影部分的面积是多少平方厘米?
参考答案
1.【答案】半径;扇形
2.【答案】45
3.【答案】
4.【答案】半径;圆上;曲线
5.【答案】;72
6.【答案】半径;r;d;d=2r;扇形;圆心角;弧
7.【答案】
8.【答案】(1)解:.14×(25.12÷3.14÷2)2
=3.14×42
=3.14×16
=50.24(平方厘米)
360×
=360×
=90(度);
答:圆心角∠AOB的度数是90度。
(2)解:25.12×
=
=6.28(厘米);
答:弧AB长6.28厘米.
9.【答案】解:扇子的半径:50.24÷(2×3.14)=50.24÷6.28=8(厘米);扇子的面积:3.14×82=3.14×64=200.96(平方厘米);答:这把扇子的面积是200.96平方厘米。
10.【答案】28.26平方厘米
11.【答案】2.28
12.【答案】113.04
13.【答案】26.4
14.【答案】1:3
15.【答案】8
16.【答案】解:3.14×42÷4
=3.14×16÷4
=50.24÷4
=12.56(平方厘米)
17.【答案】解:令大、中、小半圆的半径分别为4、3、1。
阴影部分面积:S1=1×1×π××3+(4×4×π-3×3×π)
=π+π
=5π
空白部分面积:S2=4×4×π-5π
=11π
S1:S2=5π:11π=5:11
答:涂有阴影的部分与未涂阴影的部分的面积比是5:11。
18.【答案】解:3.14×4×2÷4+5+6
=12.56×2÷4+5+6
=25.12÷4+5+6
=6.28+5+6
=11.28+6
=17.28(cm)
(4+6)×4÷2-3.14×42÷4
=10×4÷2-3.14×16÷4
=40÷2-50.24÷4
=20-12.56
=7.44(cm2)
19.【答案】解:如图所示:
×3.14×42+×3.14×(4÷2)2-×4×4
=×3.14×16+×3.14×4-2×4
=3.14×2+3.14×2-8
=6.28+6.28-8
=12.56-8
=4.56(平方厘米)
