完全平方[上学期]
图片预览





文档简介
课件19张PPT。清港中学:杨连青热烈欢迎各位
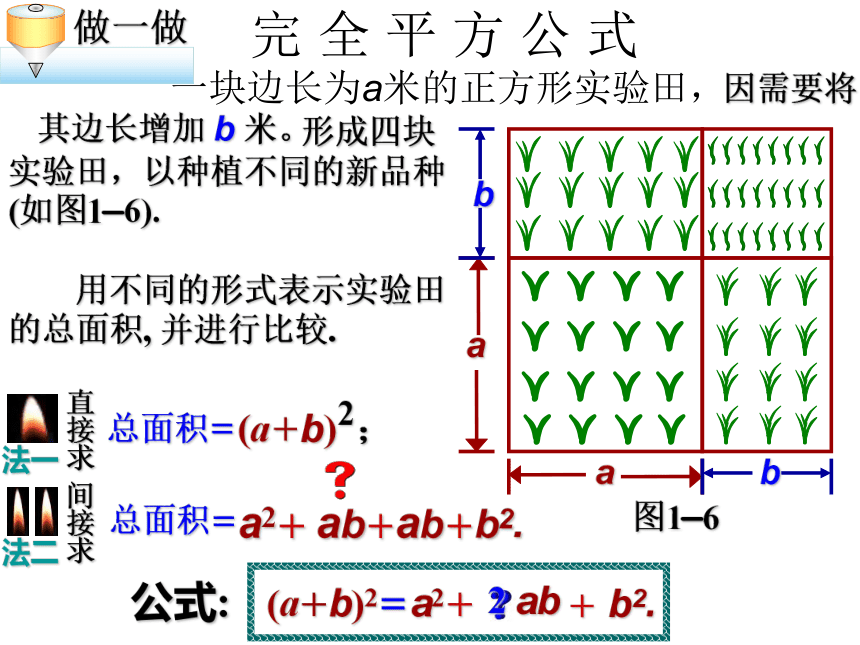
老师莅临指导!15.3.2 完全平方公式回顾与思考公式的结构特征:左边是a2 ? b2; 两个二项式的乘积,平方差公式 (a+b)(a?b)=即两数和与这两数差的积.右边是两数的平方差. 完 全 平 方 公 式 一块边长为a米的正方形实验田,图1—6 因需要将其边长增加 b 米。 形成四块实验田,以种植不同的新品种(如图1—6). 用不同的形式表示实验田的总面积, 并进行比较. (a+b) ;2a2+ab+ab+b2.(a+b)2=a2+ab+b2.2 完全平方公式 (1) 你能用多项式的乘法法则来说明它成立吗?(a+b)2=a2+2ab+b2 ;(a+b)(a+b)=a2+ab+ab+b2=a2+2ab+b2;(2)a2 ?2ab+b2.小颖写出了如下的算式:(a?b)2=[a+(?b)]2?她是怎么想的?利用两数和的
完全平方公式
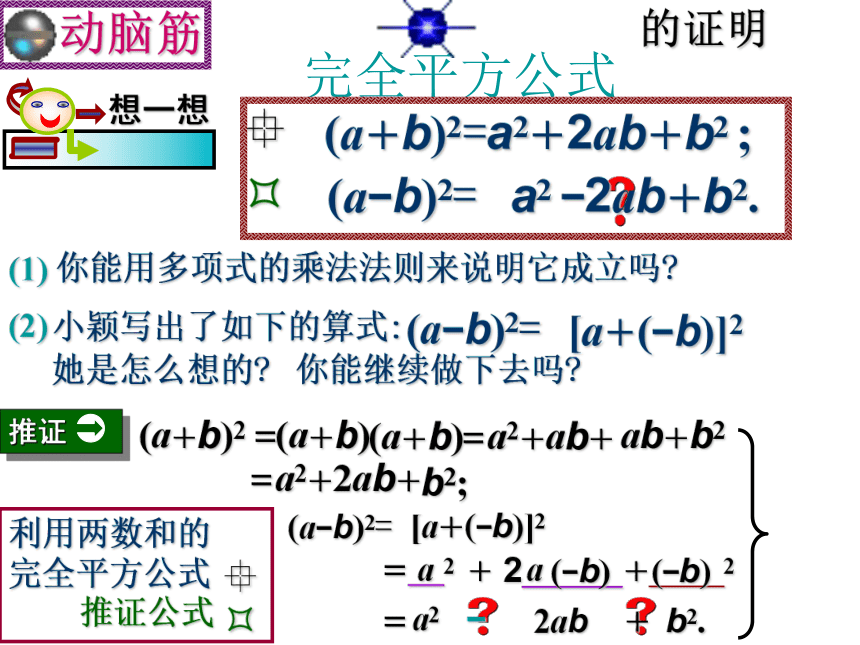
?推证公式?= 2 + 2 + 2 aa(?b)(?b)=a22ab?b2.+你能继续做下去吗?的证明公式特点:4、公式中的字母a,b可以表示数,单项式和
多项式。(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b21、积为二次三项式;2、积中两项为两数的平方和;3、另一项是两数积的2倍,且与乘式中间的符 号相同。首平方,末平方,首尾两倍中间放,符号与前一个样解: (4m+n)2= (a+b)2=a2+2ab+b2(1)(4m+n)2 ( a+ b)2= a2 + 2 a b + b2=16m2+8mn+n2(4m)2+2 4m ·n + n2例1 运用完全平方公式计算:(1) (2x+3y)2(2) (2x-3y)2(3) (-2x+3y)2(4) (-2x-3y)2小结:当所给的二项式中两项符号相同时,一般选用“和”的完全平方公式;
当所给的二项式中两项的符号相反时,一般选用“差”的完全平方差公式.变一变,你还能做吗? ?思考(a+b)2 与(-a-b)2相等吗?
(a-b)2与(b-a)2相等吗?
(a-b)2 与 a2-b2相等吗?不相等相等相等解题时常用结论:(-a-b)2 =(a+b)2 (a-b)2 =(b-a)2一试身手 (1) (y-5)2
1、利用完全平方公式计算:(2) (-4x+2y)2.
(3) (-2n -3)2 ;
(4) ( x ? 2y)2 ;填空:-2x4-4ab综合尝试,实践应用-2ab下列计算是否正确?如不正确,应怎样改正?
1.(a-2)2=a2-4 ( )
2.(2x+5)2=2x2+20x+25 ( )
3. (6a+3b)2=36a2 +18ab+9b2 ( )
4. (-a-b)(a+b)=-a2-2ab-b2 ( )×××对让我们大家一起来想!如果x2-6x+N是一个完全平方式,那么N是( )
(A )-3 (B)3 (C)-9 (D)9 D运用公式计算:
1.(a-b)(a+b)(a2+b2)2.(2-1)(2+1)(22+1) (24+1)…… (232+1)+1计算:20082-2009×2007解:原式=20082-(2008+1)(2008-1)=20082-(20082-1)=20082-20082+1=1计算:
1.(a+b+c)2
2.(x+2y-3)(x+2y+3)
本节课你的收获是什么?本节课你学到了什么?完全平方公式的结果 是三项,
即 (a ?b)2=a2 ?2ab+b2;平方差公式的结果 是两项,
即 (a+b)(a?b)=a2?b2.4计算数的平方时,可考虑把数分成两数的和(或差),
再用完全平方公式来计算,往往带来方便。
老师莅临指导!15.3.2 完全平方公式回顾与思考公式的结构特征:左边是a2 ? b2; 两个二项式的乘积,平方差公式 (a+b)(a?b)=即两数和与这两数差的积.右边是两数的平方差. 完 全 平 方 公 式 一块边长为a米的正方形实验田,图1—6 因需要将其边长增加 b 米。 形成四块实验田,以种植不同的新品种(如图1—6). 用不同的形式表示实验田的总面积, 并进行比较. (a+b) ;2a2+ab+ab+b2.(a+b)2=a2+ab+b2.2 完全平方公式 (1) 你能用多项式的乘法法则来说明它成立吗?(a+b)2=a2+2ab+b2 ;(a+b)(a+b)=a2+ab+ab+b2=a2+2ab+b2;(2)a2 ?2ab+b2.小颖写出了如下的算式:(a?b)2=[a+(?b)]2?她是怎么想的?利用两数和的
完全平方公式
?推证公式?= 2 + 2 + 2 aa(?b)(?b)=a22ab?b2.+你能继续做下去吗?的证明公式特点:4、公式中的字母a,b可以表示数,单项式和
多项式。(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b21、积为二次三项式;2、积中两项为两数的平方和;3、另一项是两数积的2倍,且与乘式中间的符 号相同。首平方,末平方,首尾两倍中间放,符号与前一个样解: (4m+n)2= (a+b)2=a2+2ab+b2(1)(4m+n)2 ( a+ b)2= a2 + 2 a b + b2=16m2+8mn+n2(4m)2+2 4m ·n + n2例1 运用完全平方公式计算:(1) (2x+3y)2(2) (2x-3y)2(3) (-2x+3y)2(4) (-2x-3y)2小结:当所给的二项式中两项符号相同时,一般选用“和”的完全平方公式;
当所给的二项式中两项的符号相反时,一般选用“差”的完全平方差公式.变一变,你还能做吗? ?思考(a+b)2 与(-a-b)2相等吗?
(a-b)2与(b-a)2相等吗?
(a-b)2 与 a2-b2相等吗?不相等相等相等解题时常用结论:(-a-b)2 =(a+b)2 (a-b)2 =(b-a)2一试身手 (1) (y-5)2
1、利用完全平方公式计算:(2) (-4x+2y)2.
(3) (-2n -3)2 ;
(4) ( x ? 2y)2 ;填空:-2x4-4ab综合尝试,实践应用-2ab下列计算是否正确?如不正确,应怎样改正?
1.(a-2)2=a2-4 ( )
2.(2x+5)2=2x2+20x+25 ( )
3. (6a+3b)2=36a2 +18ab+9b2 ( )
4. (-a-b)(a+b)=-a2-2ab-b2 ( )×××对让我们大家一起来想!如果x2-6x+N是一个完全平方式,那么N是( )
(A )-3 (B)3 (C)-9 (D)9 D运用公式计算:
1.(a-b)(a+b)(a2+b2)2.(2-1)(2+1)(22+1) (24+1)…… (232+1)+1计算:20082-2009×2007解:原式=20082-(2008+1)(2008-1)=20082-(20082-1)=20082-20082+1=1计算:
1.(a+b+c)2
2.(x+2y-3)(x+2y+3)
本节课你的收获是什么?本节课你学到了什么?完全平方公式的结果 是三项,
即 (a ?b)2=a2 ?2ab+b2;平方差公式的结果 是两项,
即 (a+b)(a?b)=a2?b2.4计算数的平方时,可考虑把数分成两数的和(或差),
再用完全平方公式来计算,往往带来方便。
