山东省威海市文登区五四学制2022-2023学年七年级下学期期末数学试题(含答案)
文档属性
| 名称 | 山东省威海市文登区五四学制2022-2023学年七年级下学期期末数学试题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 510.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-04 00:00:00 | ||
图片预览


文档简介
2022~2023学年第二学期教学质量检测
初二数学
注意事项:
1.本试卷共6页,共120分。考试时间120分钟。
2.答题前,请务必用0.5毫米黑色签字笔将自己的姓名、准考证号、座号填写在答题卡和试卷规定的位置上。
3.选择题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案标号。
4.非选择题必须使用0.5毫米黑色签字笔作答,如需改动,先划掉原来的答案,然后再写上新的答案,不能使用涂改液、胶带纸、修正带。不要求保留精确度的题目,计算结果保留准确值。
5.写在试卷上或答题卡指定区域以外的答案一律无效。
一、选择题(本大题共10小题,每小题3分,共30分。下列各题所给出的四个选项中,只有一个是正确的,每小题选对得3分,选错、不选或多选,均不得分)
1.二元一次方程的正整数解有( )
A.1个 B.2个 C.3个 D.4个
2.桌面上倒扣着5张扑克牌,其中3张红桃,2张黑桃,它们背面图案相同。从中随机抽取3张,下列事件是必然事件的是( )
A.至少有一张红桃 B.至少有一张黑桃 C.摸出三张黑桃 D.至少两张红桃
3.用“代入消元法”解方程组时,把①代入②,正确的是( )
A. B. C. D.
4.一个小球在如图所示的地面上自由滚动,小球停在阴影区域的概率为( )
A. B. C. D.
5.如图,下列选项不能判断的是( )
A. B. C. D.
6.我国古代数学名著《九章算术》中记载:“今有共买物,人出八,盈三:人出七,不足四。问人数、物价各几何?”大意是:现在有数人一起去买某物品,如果每人出8钱,则多了3钱:如果每人出7钱,则少了4钱.问共有多少人?物品的价格是多少钱?若设共有x人,物品的价格为y钱,可列方程组( )
A. B. C. D.
7.下列选项中,可以用来证明命运“若,则”是假命题的反例是( )
A., B., C., D.,
8.如图,已知,按照以下步聚作图:①以点为圆心,任意长为半径画弧,分别交OA,OB于点C,D;②分别以点C,D为圆心,以大于的长为半径画弧,两弧交于点;③连接OE,CE,DE,CD.下列结论错误的是( )
A. B. C. D.
9.设x,y,z是实数,则下列结论正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
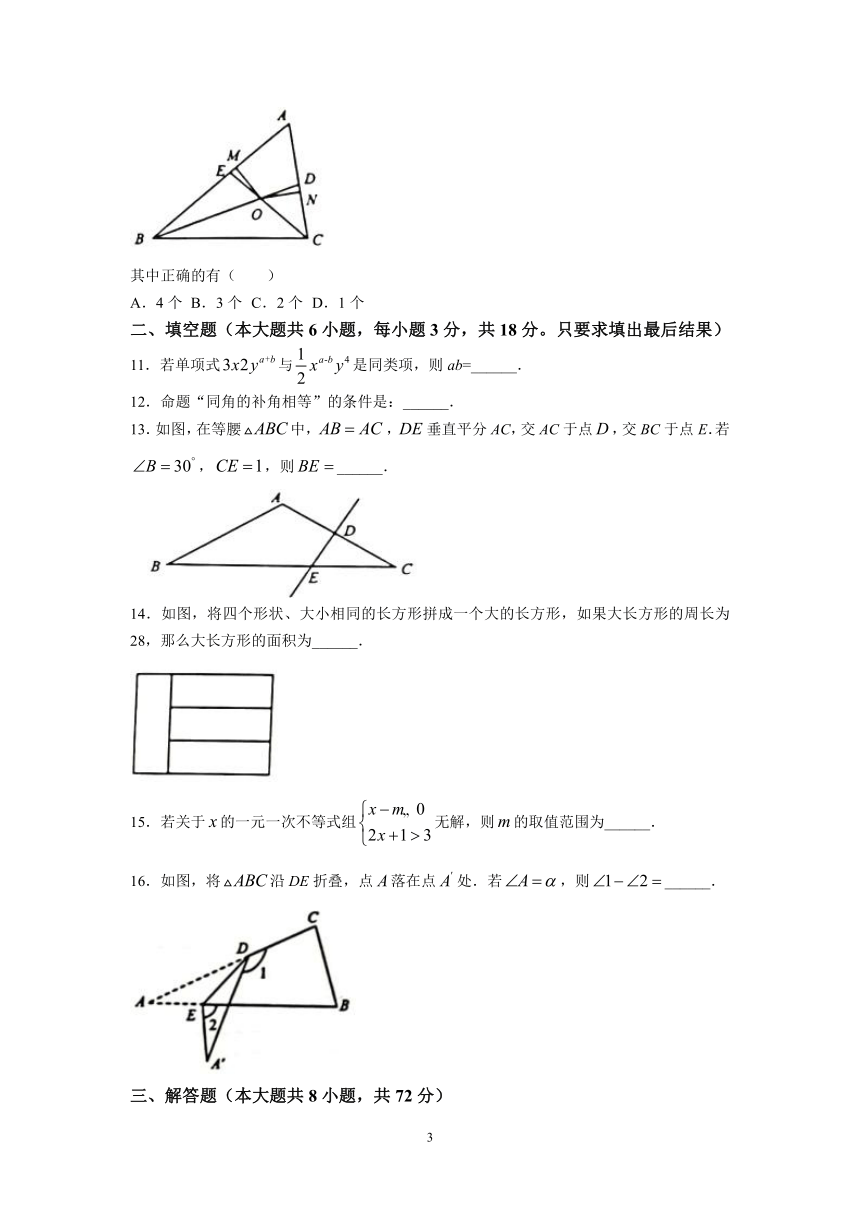
10.如图,在中,,,,分别是和的角平分线,BD,CE交于点,分别过点作于点,作于点.下列结论:
①;②;③;④.
其中正确的有( )
A.4个 B.3个 C.2个 D.1个
二、填空题(本大题共6小题,每小题3分,共18分。只要求填出最后结果)
11.若单项式与是同类项,则ab=______.
12.命题“同角的补角相等”的条件是:______.
13.如图,在等腰中,,垂直平分AC,交AC于点,交BC于点E.若,,则______.
14.如图,将四个形状、大小相同的长方形拼成一个大的长方形,如果大长方形的周长为28,那么大长方形的面积为______.
15.若关于的一元一次不等式组无解,则的取值范围为______.
16.如图,将沿DE折叠,点落在点处.若,则______.
三、解答题(本大题共8小题,共72分)
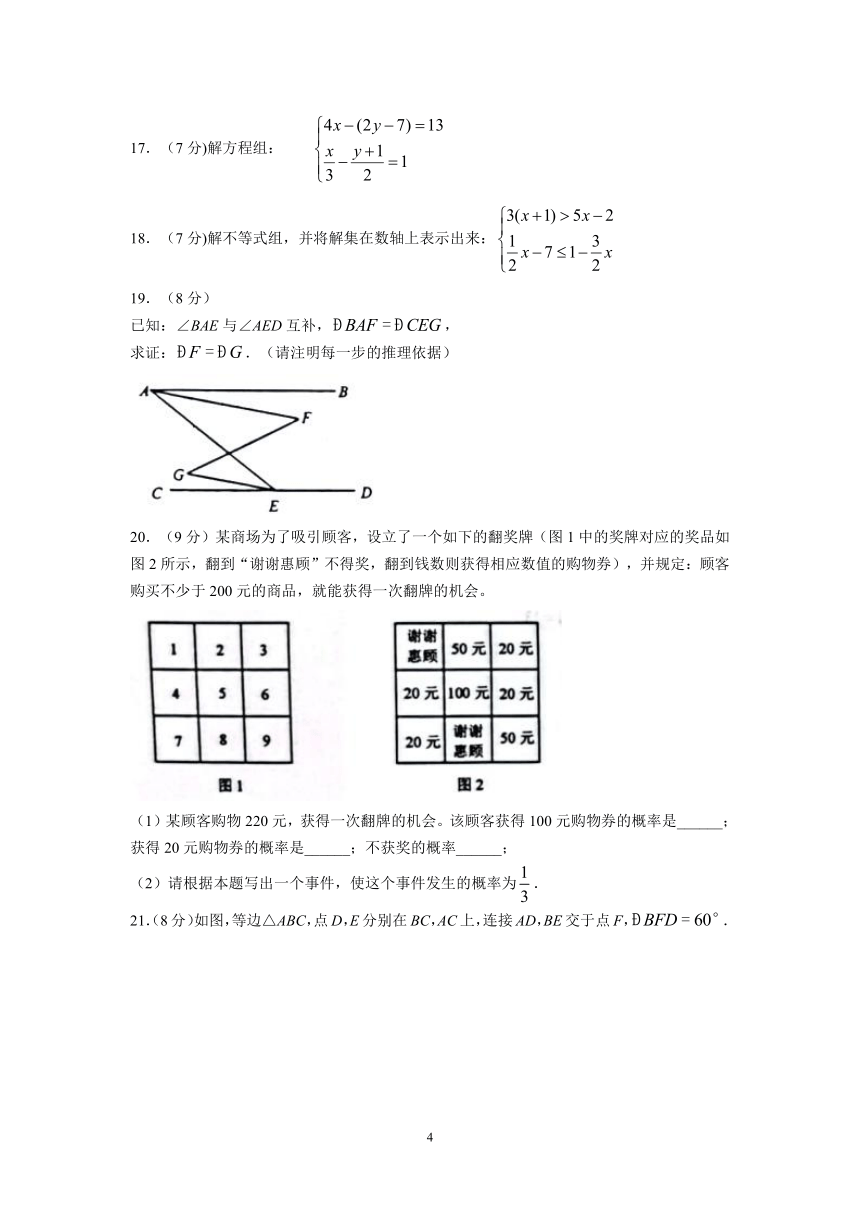
17.(7分)解方程组:
18.(7分)解不等式组,并将解集在数轴上表示出来:
19.(8分)
已知:∠BAE与∠AED互补,,
求证:.(请注明每一步的推理依据)
20.(9分)某商场为了吸引顾客,设立了一个如下的翻奖牌(图1中的奖牌对应的奖品如图2所示,翻到“谢谢惠顾”不得奖,翻到钱数则获得相应数值的购物券),并规定:顾客购买不少于200元的商品,就能获得一次翻牌的机会。
(1)某顾客购物220元,获得一次翻牌的机会。该顾客获得100元购物券的概率是______;获得20元购物券的概率是______;不获奖的概率______;
(2)请根据本题写出一个事件,使这个事件发生的概率为.
21.(8分)如图,等边△ABC,点D,E分别在BC,AC上,连接AD,BE交于点F,.
求证:。
22.(9分)从小明家到公园有一段上坡路和一段平路。周末,小明到公园玩耍,如果上坡路每小时走3千米,平路每小时走4千米,下坡路每小时走5千米,小明从家到公园需要1小时,从公园回到家需要48分钟。请问从小明家到公园的上坡路和平路各多少千米。
23.(12分)一条公路沿途有A,B,C三地,甲、乙两车分别从A,B两地同时出发,匀速行驶前往C地。乙车到达C地后停留1小时,然后以与来时相同的速度按原路返回B地。两车与C地的距离y(km)与甲车出发的时间x(h)之间的关系如图所示;
(1)甲、乙两车前往C地的速度分别为______、______;
(2)直接写出甲车行驶过程中,y(km)与x(h)之间的函数关系式______;
乙车从B地到C地的过程中,y(km)与x(h)之间的函数关系式______;
(3)甲车出发多少小时后与乙车相遇?此时两车到C地的距离为多少?
24.(12分)如图,在△ABC中,,。点D是BC上一点,以AD为边作△ADE,使,.连接CE并延长,过点A作AF⊥CE的延长线于点F.
(1)判断△ACF的形状,并说明理由:
(2)求证:.
2022~2023学年第二学期教学质量检测
初二数学答案
1.全卷总分120分.
2.该答案较略,仅供参考,解答题建议中间步骤适当给分,培养学生重视解题步骤的好习惯.
3.对不同方法,可研究、酌情给分.
4.若答案中出现了较明显的错误,请各位老师商议后进行改正.
一、选择题(本大题共10小题,每小题3分,共30分.下列各题所给出的四个选项中,只有一个是正确的,每小题选对得3分,选错、不选或多选,均不得分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C A B B C D A B D A
二、填空题(本大题共6小题,每小题3分,共18分.只要求填出最后结果)
11.3 12.两个角是同一个角的补角13.2 14.48 15. 16.
三、解答题(本大题共8小题,共72分)
17.(7分)
原方程组可化为解得
18.(7分)
由①得,;由②得,;
数轴表示(略)
所以原不等式组的解集为
19.(8分)
证出
求出
求出
注:推理依据每错两个扣1分。
20.(9分)
(1),,(2)略
21.(8分)
证出 证出 得出
22.(9分)
设:从小明家到公园的上坡路为x千米,平路为y千米,由题意得
解得
答:(略)。
23.(12分)
(1)60km/h、100km/h;
(2);;
(3)求出乙车从C地返回B地y(km)与x(h)之间的函数关系式:;
列方程组解得
答:(略)。
24.(12分)
(1)△ACF为等腰直角三角形。
证出
得出
证出△ACF为等腰直角三角形.
(2)延长CF至点G,使,连接AG.
证出
证出
证出
初二数学
注意事项:
1.本试卷共6页,共120分。考试时间120分钟。
2.答题前,请务必用0.5毫米黑色签字笔将自己的姓名、准考证号、座号填写在答题卡和试卷规定的位置上。
3.选择题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案标号。
4.非选择题必须使用0.5毫米黑色签字笔作答,如需改动,先划掉原来的答案,然后再写上新的答案,不能使用涂改液、胶带纸、修正带。不要求保留精确度的题目,计算结果保留准确值。
5.写在试卷上或答题卡指定区域以外的答案一律无效。
一、选择题(本大题共10小题,每小题3分,共30分。下列各题所给出的四个选项中,只有一个是正确的,每小题选对得3分,选错、不选或多选,均不得分)
1.二元一次方程的正整数解有( )
A.1个 B.2个 C.3个 D.4个
2.桌面上倒扣着5张扑克牌,其中3张红桃,2张黑桃,它们背面图案相同。从中随机抽取3张,下列事件是必然事件的是( )
A.至少有一张红桃 B.至少有一张黑桃 C.摸出三张黑桃 D.至少两张红桃
3.用“代入消元法”解方程组时,把①代入②,正确的是( )
A. B. C. D.
4.一个小球在如图所示的地面上自由滚动,小球停在阴影区域的概率为( )
A. B. C. D.
5.如图,下列选项不能判断的是( )
A. B. C. D.
6.我国古代数学名著《九章算术》中记载:“今有共买物,人出八,盈三:人出七,不足四。问人数、物价各几何?”大意是:现在有数人一起去买某物品,如果每人出8钱,则多了3钱:如果每人出7钱,则少了4钱.问共有多少人?物品的价格是多少钱?若设共有x人,物品的价格为y钱,可列方程组( )
A. B. C. D.
7.下列选项中,可以用来证明命运“若,则”是假命题的反例是( )
A., B., C., D.,
8.如图,已知,按照以下步聚作图:①以点为圆心,任意长为半径画弧,分别交OA,OB于点C,D;②分别以点C,D为圆心,以大于的长为半径画弧,两弧交于点;③连接OE,CE,DE,CD.下列结论错误的是( )
A. B. C. D.
9.设x,y,z是实数,则下列结论正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
10.如图,在中,,,,分别是和的角平分线,BD,CE交于点,分别过点作于点,作于点.下列结论:
①;②;③;④.
其中正确的有( )
A.4个 B.3个 C.2个 D.1个
二、填空题(本大题共6小题,每小题3分,共18分。只要求填出最后结果)
11.若单项式与是同类项,则ab=______.
12.命题“同角的补角相等”的条件是:______.
13.如图,在等腰中,,垂直平分AC,交AC于点,交BC于点E.若,,则______.
14.如图,将四个形状、大小相同的长方形拼成一个大的长方形,如果大长方形的周长为28,那么大长方形的面积为______.
15.若关于的一元一次不等式组无解,则的取值范围为______.
16.如图,将沿DE折叠,点落在点处.若,则______.
三、解答题(本大题共8小题,共72分)
17.(7分)解方程组:
18.(7分)解不等式组,并将解集在数轴上表示出来:
19.(8分)
已知:∠BAE与∠AED互补,,
求证:.(请注明每一步的推理依据)
20.(9分)某商场为了吸引顾客,设立了一个如下的翻奖牌(图1中的奖牌对应的奖品如图2所示,翻到“谢谢惠顾”不得奖,翻到钱数则获得相应数值的购物券),并规定:顾客购买不少于200元的商品,就能获得一次翻牌的机会。
(1)某顾客购物220元,获得一次翻牌的机会。该顾客获得100元购物券的概率是______;获得20元购物券的概率是______;不获奖的概率______;
(2)请根据本题写出一个事件,使这个事件发生的概率为.
21.(8分)如图,等边△ABC,点D,E分别在BC,AC上,连接AD,BE交于点F,.
求证:。
22.(9分)从小明家到公园有一段上坡路和一段平路。周末,小明到公园玩耍,如果上坡路每小时走3千米,平路每小时走4千米,下坡路每小时走5千米,小明从家到公园需要1小时,从公园回到家需要48分钟。请问从小明家到公园的上坡路和平路各多少千米。
23.(12分)一条公路沿途有A,B,C三地,甲、乙两车分别从A,B两地同时出发,匀速行驶前往C地。乙车到达C地后停留1小时,然后以与来时相同的速度按原路返回B地。两车与C地的距离y(km)与甲车出发的时间x(h)之间的关系如图所示;
(1)甲、乙两车前往C地的速度分别为______、______;
(2)直接写出甲车行驶过程中,y(km)与x(h)之间的函数关系式______;
乙车从B地到C地的过程中,y(km)与x(h)之间的函数关系式______;
(3)甲车出发多少小时后与乙车相遇?此时两车到C地的距离为多少?
24.(12分)如图,在△ABC中,,。点D是BC上一点,以AD为边作△ADE,使,.连接CE并延长,过点A作AF⊥CE的延长线于点F.
(1)判断△ACF的形状,并说明理由:
(2)求证:.
2022~2023学年第二学期教学质量检测
初二数学答案
1.全卷总分120分.
2.该答案较略,仅供参考,解答题建议中间步骤适当给分,培养学生重视解题步骤的好习惯.
3.对不同方法,可研究、酌情给分.
4.若答案中出现了较明显的错误,请各位老师商议后进行改正.
一、选择题(本大题共10小题,每小题3分,共30分.下列各题所给出的四个选项中,只有一个是正确的,每小题选对得3分,选错、不选或多选,均不得分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C A B B C D A B D A
二、填空题(本大题共6小题,每小题3分,共18分.只要求填出最后结果)
11.3 12.两个角是同一个角的补角13.2 14.48 15. 16.
三、解答题(本大题共8小题,共72分)
17.(7分)
原方程组可化为解得
18.(7分)
由①得,;由②得,;
数轴表示(略)
所以原不等式组的解集为
19.(8分)
证出
求出
求出
注:推理依据每错两个扣1分。
20.(9分)
(1),,(2)略
21.(8分)
证出 证出 得出
22.(9分)
设:从小明家到公园的上坡路为x千米,平路为y千米,由题意得
解得
答:(略)。
23.(12分)
(1)60km/h、100km/h;
(2);;
(3)求出乙车从C地返回B地y(km)与x(h)之间的函数关系式:;
列方程组解得
答:(略)。
24.(12分)
(1)△ACF为等腰直角三角形。
证出
得出
证出△ACF为等腰直角三角形.
(2)延长CF至点G,使,连接AG.
证出
证出
证出
同课章节目录
