人教版七年级数学上册3.2.2一元一次方程的解法(一)移项课件(22张PPT)
文档属性
| 名称 | 人教版七年级数学上册3.2.2一元一次方程的解法(一)移项课件(22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-05 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
第3章 一元一次方程
3.2.2一元一次方程的解法(一)
---移项
第三单元
1.理解移项的意义,掌握移项的方法.
2.学会运用移项解形如“ax+b=cx+d”的一元一次方程.
3.能够抓住实际问题中的数量关系列一元一次方程解决实际问题.
解下列方程:
(1)4x-9x=10; (2)-y+y=5; (3)+x+2x=210; (4)-=-5.
(1)解:合并同类项,得
-5x=10
系数化为1,得
x=-2
(2)解:合并同类项,得
-y=5
系数化为1,得
y=-5
(3)解:合并同类项,得
x=210
系数化为1,得
x=60
(4)解:合并同类项,得
=-5
系数化为1,得
x=-30
问题:把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少名学生?
解:设这个班有x名学生.
每人分3本,共分出____本,加上剩余的20本,这批书共____________本.
每人分4本,需要______本,减去缺的25本,这批书共______________本.
这批书的总数是一个定值,表示它的两个式子应相等,即表示同一个量的两个不同的式子相等.根据这一相等关系列方程得:
这批书的总数有几种表示法?它们之间有什么关系?本题哪个相等关系可作为列方程的依据呢?
方程3x+20=4x-25的两边都有含x的项(3x与4x)和不含字母的常数项(20与-25),怎样才能使它向x=a(常数)的形式转化呢?
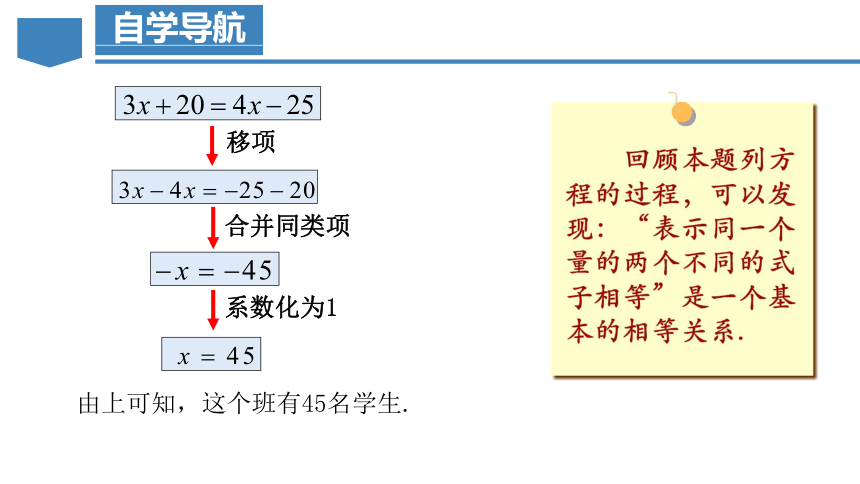
3x+20=4x-25
3x-4x+20=4x-4x-25
3x-4x=-25-20
3x-4x+20=-25
3x-4x+20-20=-25-20
比较下面的两个方程,你发现了什么?
移项的定义
一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项.
注意:移项一定要变号
移项的依据及注意事项
移项实际上是利用等式的性质1.
移项
合并同类项
系数化为1
由上可知,这个班有45名学生.
下面解方程中“移项”起了什么作用?
移项
合并同类项
系数化为1
通过移项,含未知数的项与常数项分别位于方程左右两边,使方程更接近于x=a的形式.
解方程时经常要“合并同类项”和“移项”,前面提到的古老的代数书中的“对消”和“还原”,指的就是“合并同类项”和“移项”. 早在一千多年前,数学家阿尔-花拉子米就已经对“合并同类项”和“移项”非常重视了.
利用移项解一元一次方程
重点
例1.解下列方程:
(1)2x-6=4x-1; (2)x-6=-x+4.
解:(1)移项,得
2x-4x=-1+6.
合并同类项,得
-2x=5.
系数化为1,得
x=-.
注意:改变了符号.
(2)移项,得
x+x=4+6.
合并同类项,得
x=10.
系数化为1,得
x=12.
1.解方程5x-3=2x+2,移项正确的是( )
A.5x-2x=2+3 B.5x+2x=2+3 C.5x-2x=2-3 D.5x+2x=2-3
2.若x的2倍与8的和等于6与x的2倍的差,则x=_____.
3.当:x=_____时,2x-3与3x+1的值互为相反数.
4.若单项式-2a3b2n-1与am-1b3n+2的和仍是单项式,则m+n=_____.
A
-
1
5.解下列方程:
(1)4-3x=6-5x; (2)2.5m+10m-15=6m-21.5; (3)x-2=x+.
解:(1)移项,得
-3x+5x=6-4.
合并同类项,得
2x=2.
系数化为1,得
x=1.
(2)移项,得
2.5m+10m-6m=-21.5+15.
合并同类项,得
6.5m=-6.5.
系数化为1,得
m=-1.
(3)移项,得
x-x=+2.
合并同类项,得
-x=.
系数化为1,得
x=-.
根据“表示同一个量的两个不同的式子相等”列方程解决问题
重点
例2.七年级(2)班全班同学去郊游,需要一定费用,如果每位同学付5元,那么还差5.6元;如果每位同学付5.5元,那么就多出10.4元.这个班有多少名同学 总费用是多少元
根据“表示同一个量的两个不同的式子相等”列方程解决问题
重点
例2.七年级(2)班全班同学去郊游,需要一定费用,如果每位同学付5元,那么还差5.6元;如果每位同学付5.5元,那么就多出10.4元.这个班有多少名同学 总费用是多少元
解:设这个班有x名同学.
根据题意,得5x+5.6=5.5x-10.4.
移项,得5x-5.5x=-10.4-5.6.
合并同类项,得-0.5x=-16.
系数化为1 ,得x=32.
所以5x+5.6=165.6.答:这个班有32名同学,总费用为165.6元.
1.甲仓库有200t煤,乙仓库有80t煤,若甲仓库每天运出15t煤,乙仓库每天运进25t煤,则_____天后两仓库存煤量相等.
2.《九章算术》中有一个“盈不足术”的问题,其大意是:若干人共同出资买羊,每人出5钱,则差45钱;每人出7钱,则差3钱.问:人数和羊价各是多少
3
解:设人数为x.根据题意,有5x+45=7x+3.
移项,得5x-7x=3-45.
合并同类项,得-2x=-42.
系数化为1, 得x=21.所以5x+45=150.答:人数为21,羊价为150钱.
利用一元一次方程解决数字问题
重点
例3.一个两位数,个位上的数是十位上的数的2倍,如果把十位上的数与个位上的数交换位置,所得的新两位数比原两位数大27,求原两位数的大小.
分析:设原两位数十位,上的数为x.
相等关系:新两位数=原两位数+27.
利用一元一次方程解决数字问题
重点
例3.一个两位数,个位上的数是十位上的数的2倍,如果把十位上的数与个位上的数交换位置,所得的新两位数比原两位数大27,求原两位数的大小.
解:设原两位数十位上的数为x,则个位上的数为2x.
根据题意,得10×2x+x=10x+2x+27.
移项,得20x+x-10x-2x=27.
合并同类项,得9x=27.
系数化为1,得x=3.
所以2x=6.
答:原两位数为36.
1.如图,在编写数学谜题时,“□”内要求填写同一个数字,若设“□”内的数字为x.则列出的方程正确的是( )
A.3×2x+5=2x B.3×20x+5=10x×2
C.3×20+x+5=20x D.3(20+x)+5=10x+2
2.有一个两位数,个位上的数比十位上的数大4,且个位上的数与十位上的数的和比这个两位数小9.求这个两位数.
解:设这个两位数十位上的数为x,则个位上的数为x+4.
根据题意,得x+4+x=10x+x+4-9,解得x=1.
所以x+4=5.答:这个两位数为15.
D
利用方程解决数字规律问题
难点
例4.在如图的月历表中,任意框出表中竖列上三个相邻的数,这三个数的和可能是( )
A.28 B.54 C.65 D.75
月历中数的关系:同一行中,相邻两数相差1;同一列中,相邻两数相差7.
另外,月历上的日期数最小为1,日 期数的最大值(不超过31)与月份有关,且日期数都是正整数.
解析:设三个数中中间的数为2x,则最小的数为x-7,最大的数为x+7,所以三个数的和为(x-7)+x+(x+7)=3x.故三个数的和是3的倍数.
例4.在如图的月历表中,任意框出表中竖列上三个相邻的数,这三个数的和可能是( )
A.28 B.54 C.65 D.75
B
利用方程解决数字规律问题
难点
1.小明在某月的日历上圈出了三个数a,b,c,并求出了它们的和为39,则这三个数在日历中的排列位置不可能是( )
B
2.如图,规定:上方相邻两数之和等于这两数下方箭头共同指向的数.
(1)用含有x的式子表示:m=_____,n=________;
(2)若y=-2,求x的值.
3x
2x+3
解:由题意得m=3x,n=2x+3,y=m+n,因为y=-2,所以3x+2x+3=-2.
解得x=-1.
移项的定义
一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项.
注意:移项一定要变号
移项的依据及注意事项
移项实际上是利用等式的性质1.
第3章 一元一次方程
3.2.2一元一次方程的解法(一)
---移项
第三单元
1.理解移项的意义,掌握移项的方法.
2.学会运用移项解形如“ax+b=cx+d”的一元一次方程.
3.能够抓住实际问题中的数量关系列一元一次方程解决实际问题.
解下列方程:
(1)4x-9x=10; (2)-y+y=5; (3)+x+2x=210; (4)-=-5.
(1)解:合并同类项,得
-5x=10
系数化为1,得
x=-2
(2)解:合并同类项,得
-y=5
系数化为1,得
y=-5
(3)解:合并同类项,得
x=210
系数化为1,得
x=60
(4)解:合并同类项,得
=-5
系数化为1,得
x=-30
问题:把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少名学生?
解:设这个班有x名学生.
每人分3本,共分出____本,加上剩余的20本,这批书共____________本.
每人分4本,需要______本,减去缺的25本,这批书共______________本.
这批书的总数是一个定值,表示它的两个式子应相等,即表示同一个量的两个不同的式子相等.根据这一相等关系列方程得:
这批书的总数有几种表示法?它们之间有什么关系?本题哪个相等关系可作为列方程的依据呢?
方程3x+20=4x-25的两边都有含x的项(3x与4x)和不含字母的常数项(20与-25),怎样才能使它向x=a(常数)的形式转化呢?
3x+20=4x-25
3x-4x+20=4x-4x-25
3x-4x=-25-20
3x-4x+20=-25
3x-4x+20-20=-25-20
比较下面的两个方程,你发现了什么?
移项的定义
一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项.
注意:移项一定要变号
移项的依据及注意事项
移项实际上是利用等式的性质1.
移项
合并同类项
系数化为1
由上可知,这个班有45名学生.
下面解方程中“移项”起了什么作用?
移项
合并同类项
系数化为1
通过移项,含未知数的项与常数项分别位于方程左右两边,使方程更接近于x=a的形式.
解方程时经常要“合并同类项”和“移项”,前面提到的古老的代数书中的“对消”和“还原”,指的就是“合并同类项”和“移项”. 早在一千多年前,数学家阿尔-花拉子米就已经对“合并同类项”和“移项”非常重视了.
利用移项解一元一次方程
重点
例1.解下列方程:
(1)2x-6=4x-1; (2)x-6=-x+4.
解:(1)移项,得
2x-4x=-1+6.
合并同类项,得
-2x=5.
系数化为1,得
x=-.
注意:改变了符号.
(2)移项,得
x+x=4+6.
合并同类项,得
x=10.
系数化为1,得
x=12.
1.解方程5x-3=2x+2,移项正确的是( )
A.5x-2x=2+3 B.5x+2x=2+3 C.5x-2x=2-3 D.5x+2x=2-3
2.若x的2倍与8的和等于6与x的2倍的差,则x=_____.
3.当:x=_____时,2x-3与3x+1的值互为相反数.
4.若单项式-2a3b2n-1与am-1b3n+2的和仍是单项式,则m+n=_____.
A
-
1
5.解下列方程:
(1)4-3x=6-5x; (2)2.5m+10m-15=6m-21.5; (3)x-2=x+.
解:(1)移项,得
-3x+5x=6-4.
合并同类项,得
2x=2.
系数化为1,得
x=1.
(2)移项,得
2.5m+10m-6m=-21.5+15.
合并同类项,得
6.5m=-6.5.
系数化为1,得
m=-1.
(3)移项,得
x-x=+2.
合并同类项,得
-x=.
系数化为1,得
x=-.
根据“表示同一个量的两个不同的式子相等”列方程解决问题
重点
例2.七年级(2)班全班同学去郊游,需要一定费用,如果每位同学付5元,那么还差5.6元;如果每位同学付5.5元,那么就多出10.4元.这个班有多少名同学 总费用是多少元
根据“表示同一个量的两个不同的式子相等”列方程解决问题
重点
例2.七年级(2)班全班同学去郊游,需要一定费用,如果每位同学付5元,那么还差5.6元;如果每位同学付5.5元,那么就多出10.4元.这个班有多少名同学 总费用是多少元
解:设这个班有x名同学.
根据题意,得5x+5.6=5.5x-10.4.
移项,得5x-5.5x=-10.4-5.6.
合并同类项,得-0.5x=-16.
系数化为1 ,得x=32.
所以5x+5.6=165.6.答:这个班有32名同学,总费用为165.6元.
1.甲仓库有200t煤,乙仓库有80t煤,若甲仓库每天运出15t煤,乙仓库每天运进25t煤,则_____天后两仓库存煤量相等.
2.《九章算术》中有一个“盈不足术”的问题,其大意是:若干人共同出资买羊,每人出5钱,则差45钱;每人出7钱,则差3钱.问:人数和羊价各是多少
3
解:设人数为x.根据题意,有5x+45=7x+3.
移项,得5x-7x=3-45.
合并同类项,得-2x=-42.
系数化为1, 得x=21.所以5x+45=150.答:人数为21,羊价为150钱.
利用一元一次方程解决数字问题
重点
例3.一个两位数,个位上的数是十位上的数的2倍,如果把十位上的数与个位上的数交换位置,所得的新两位数比原两位数大27,求原两位数的大小.
分析:设原两位数十位,上的数为x.
相等关系:新两位数=原两位数+27.
利用一元一次方程解决数字问题
重点
例3.一个两位数,个位上的数是十位上的数的2倍,如果把十位上的数与个位上的数交换位置,所得的新两位数比原两位数大27,求原两位数的大小.
解:设原两位数十位上的数为x,则个位上的数为2x.
根据题意,得10×2x+x=10x+2x+27.
移项,得20x+x-10x-2x=27.
合并同类项,得9x=27.
系数化为1,得x=3.
所以2x=6.
答:原两位数为36.
1.如图,在编写数学谜题时,“□”内要求填写同一个数字,若设“□”内的数字为x.则列出的方程正确的是( )
A.3×2x+5=2x B.3×20x+5=10x×2
C.3×20+x+5=20x D.3(20+x)+5=10x+2
2.有一个两位数,个位上的数比十位上的数大4,且个位上的数与十位上的数的和比这个两位数小9.求这个两位数.
解:设这个两位数十位上的数为x,则个位上的数为x+4.
根据题意,得x+4+x=10x+x+4-9,解得x=1.
所以x+4=5.答:这个两位数为15.
D
利用方程解决数字规律问题
难点
例4.在如图的月历表中,任意框出表中竖列上三个相邻的数,这三个数的和可能是( )
A.28 B.54 C.65 D.75
月历中数的关系:同一行中,相邻两数相差1;同一列中,相邻两数相差7.
另外,月历上的日期数最小为1,日 期数的最大值(不超过31)与月份有关,且日期数都是正整数.
解析:设三个数中中间的数为2x,则最小的数为x-7,最大的数为x+7,所以三个数的和为(x-7)+x+(x+7)=3x.故三个数的和是3的倍数.
例4.在如图的月历表中,任意框出表中竖列上三个相邻的数,这三个数的和可能是( )
A.28 B.54 C.65 D.75
B
利用方程解决数字规律问题
难点
1.小明在某月的日历上圈出了三个数a,b,c,并求出了它们的和为39,则这三个数在日历中的排列位置不可能是( )
B
2.如图,规定:上方相邻两数之和等于这两数下方箭头共同指向的数.
(1)用含有x的式子表示:m=_____,n=________;
(2)若y=-2,求x的值.
3x
2x+3
解:由题意得m=3x,n=2x+3,y=m+n,因为y=-2,所以3x+2x+3=-2.
解得x=-1.
移项的定义
一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项.
注意:移项一定要变号
移项的依据及注意事项
移项实际上是利用等式的性质1.
