长方体和正方体的认识(同步练习)-六年级上册数学苏教版(无答案)
文档属性
| 名称 | 长方体和正方体的认识(同步练习)-六年级上册数学苏教版(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 48.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-04 10:41:29 | ||
图片预览

文档简介
1.1 长方体和正方体的认识
知识点:1.认识长方体、正方体,理解长方体和正方体的面、棱、顶点以及长、宽、高(或棱长)的含义,掌握长方体和正方体的基本特点。长方体和正方体都有12条棱,6个面,8个顶点,相对的面完全一样。
2.认识四个面相等的长方体,相对的两个面是正方形,其他四个为面积相等的长方形。
3.棱长总和的求法:长方体棱长和=(长+宽+高)×4,正方体棱长和=棱长×12.
4.熟悉长方体和正方体的展开图。
基础题
填空题。
(1)一个长方体的长是15厘米,宽是12厘米,高是8厘米,它的上面的长是( )厘米,面积是( )平方厘米;前面的长是( )厘米,宽是( )厘米,面积是( )平方厘米;右面的长是( )厘米,宽是( )厘米,面积是( )平方厘米。
(2)用铁丝焊接成一个长12厘米、宽10厘米、高5厘米的长方体框架,至少需要铁丝( )厘米。
(3)一个长方体的长是9分米,宽是5分米,高是5分米,这个长方体有( )个面是正方形,每个面的面积是( )平方分米;其余四个面是长方形,其面积大小( ),每个面的面积是( )平方分米;这个长方体的表面积是( )
平方分米。
(4)一个长方体的金鱼缸,长是8分米,宽是5分米,高是6分米,不小心前面的玻璃被打坏了,修理时配上的玻璃的面积是( )。
(5)一个正方体的棱长总和是72厘米,它的一个面是边长( )厘米的正方形,它的表面积是( )平方厘米。
2.判断题。
(1)长方体的6个面一定都是长方形。 ( )
(2)长方体相对的两个面的面积一定相等。 ( )
(3)长方体的6个面中有可能有四个面是正方形。 ( )
(4)一张很薄的纸,只有正反两面。 ( )
(5)一个长方体如果有四个面是正方形,这个长方体一定是正方体。 ( )
(6)正方体的棱长扩大2倍,棱长和扩大2倍,表面积扩大2倍。
3.看图填空。
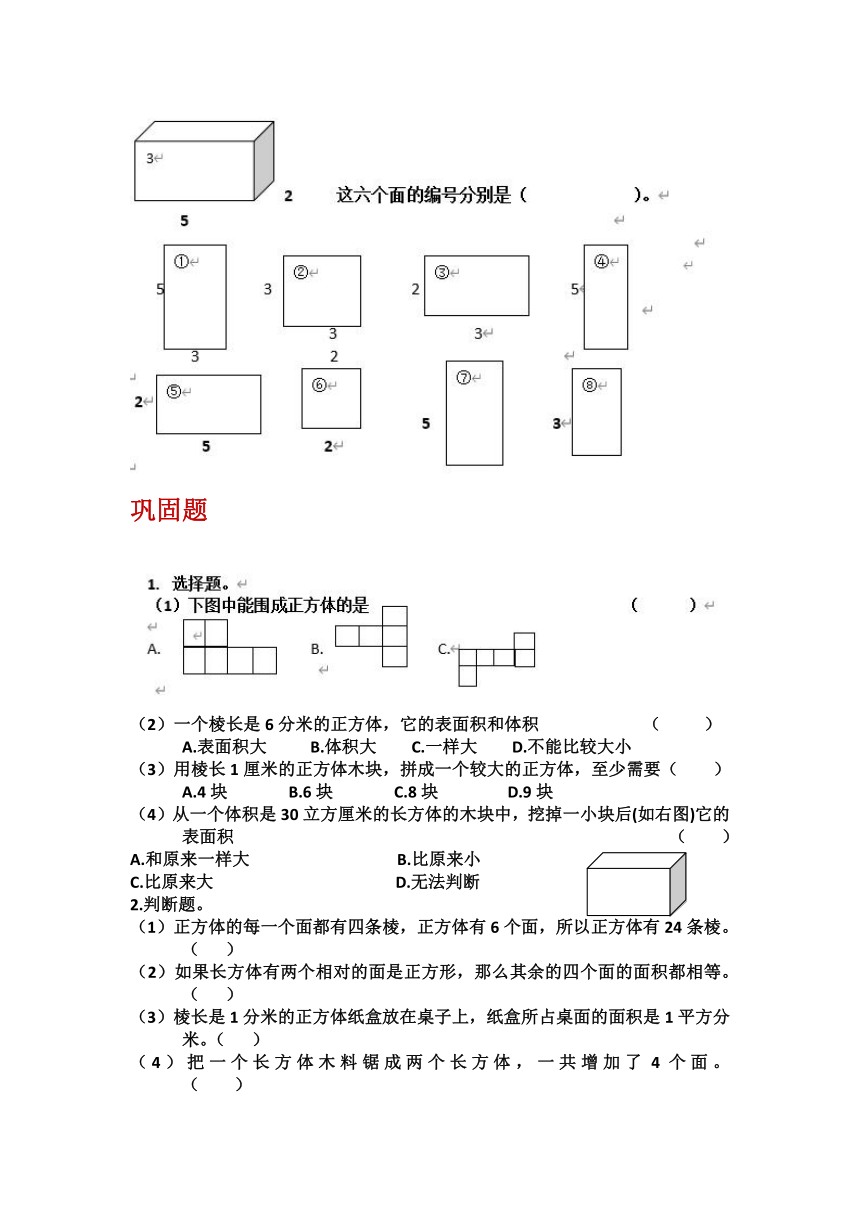
在下面的8个面中找出6个面,使它们能围成右面的长方体。
5
巩固题
(2)一个棱长是6分米的正方体,它的表面积和体积 ( )
A.表面积大 B.体积大 C.一样大 D.不能比较大小
(3)用棱长1厘米的正方体木块,拼成一个较大的正方体,至少需要( )
A.4块 B.6块 C.8块 D.9块
(4)从一个体积是30立方厘米的长方体的木块中,挖掉一小块后(如右图)它的表面积 ( )
A.和原来一样大 B.比原来小
C.比原来大 D.无法判断
2.判断题。
(1)正方体的每一个面都有四条棱,正方体有6个面,所以正方体有24条棱。( )
(2)如果长方体有两个相对的面是正方形,那么其余的四个面的面积都相等。( )
(3)棱长是1分米的正方体纸盒放在桌子上,纸盒所占桌面的面积是1平方分米。( )
(4)把一个长方体木料锯成两个长方体,一共增加了4个面。 ( )
3.应用题。
(1)将4个棱长都是2厘米的正方体如下图摆放,露在外面的面积是多少?
(2)一个长方体的棱长总和是160厘米,它的长是12厘米,宽是5厘米。这个长方体的高是多少厘米
(3)一个长方体和一个正方体的棱长之和相等,已知长方体的长为5厘米,宽为3厘米,髙为4厘米。求正方体的棱长。
(4)一个长方体木块,它的长是12厘米,宽是10厘米,高是8厘米,现把这个长方体的木块截成一个最大的正方体。这个正方体的棱长总和是多少厘米
压轴题
填空题。
把棱长8厘米的正方体木块分割成棱长2厘米的小正方体木块,可以分割成( )块。
需要( )个棱长为3厘米的正方体,才能组成一个棱长为9厘米的正方体。
操作题。
有一块形状如下图的硬纸,把它按照虚线折叠,能不能围成一个正方体?
从一个正方体上锯下一个角(一个四面体),使得剩下部分的棱长分别为12条、13条、14条、15条,应当怎样锯?清画出示意图。
12条 13条 14条 15条
(3)用一个平面去截一个正方体,可以得到几边形?
将一个长15厘米,宽6厘米,高3厘米的长方体三等分,你有几种分法?在下图中画出来。
增加的面积各是多少?
(5)用字母标出一个正方体的各面,下图中是三个不同方位的正方体。问:字母A,B,C的对面是什么字母?
知识点:1.认识长方体、正方体,理解长方体和正方体的面、棱、顶点以及长、宽、高(或棱长)的含义,掌握长方体和正方体的基本特点。长方体和正方体都有12条棱,6个面,8个顶点,相对的面完全一样。
2.认识四个面相等的长方体,相对的两个面是正方形,其他四个为面积相等的长方形。
3.棱长总和的求法:长方体棱长和=(长+宽+高)×4,正方体棱长和=棱长×12.
4.熟悉长方体和正方体的展开图。
基础题
填空题。
(1)一个长方体的长是15厘米,宽是12厘米,高是8厘米,它的上面的长是( )厘米,面积是( )平方厘米;前面的长是( )厘米,宽是( )厘米,面积是( )平方厘米;右面的长是( )厘米,宽是( )厘米,面积是( )平方厘米。
(2)用铁丝焊接成一个长12厘米、宽10厘米、高5厘米的长方体框架,至少需要铁丝( )厘米。
(3)一个长方体的长是9分米,宽是5分米,高是5分米,这个长方体有( )个面是正方形,每个面的面积是( )平方分米;其余四个面是长方形,其面积大小( ),每个面的面积是( )平方分米;这个长方体的表面积是( )
平方分米。
(4)一个长方体的金鱼缸,长是8分米,宽是5分米,高是6分米,不小心前面的玻璃被打坏了,修理时配上的玻璃的面积是( )。
(5)一个正方体的棱长总和是72厘米,它的一个面是边长( )厘米的正方形,它的表面积是( )平方厘米。
2.判断题。
(1)长方体的6个面一定都是长方形。 ( )
(2)长方体相对的两个面的面积一定相等。 ( )
(3)长方体的6个面中有可能有四个面是正方形。 ( )
(4)一张很薄的纸,只有正反两面。 ( )
(5)一个长方体如果有四个面是正方形,这个长方体一定是正方体。 ( )
(6)正方体的棱长扩大2倍,棱长和扩大2倍,表面积扩大2倍。
3.看图填空。
在下面的8个面中找出6个面,使它们能围成右面的长方体。
5
巩固题
(2)一个棱长是6分米的正方体,它的表面积和体积 ( )
A.表面积大 B.体积大 C.一样大 D.不能比较大小
(3)用棱长1厘米的正方体木块,拼成一个较大的正方体,至少需要( )
A.4块 B.6块 C.8块 D.9块
(4)从一个体积是30立方厘米的长方体的木块中,挖掉一小块后(如右图)它的表面积 ( )
A.和原来一样大 B.比原来小
C.比原来大 D.无法判断
2.判断题。
(1)正方体的每一个面都有四条棱,正方体有6个面,所以正方体有24条棱。( )
(2)如果长方体有两个相对的面是正方形,那么其余的四个面的面积都相等。( )
(3)棱长是1分米的正方体纸盒放在桌子上,纸盒所占桌面的面积是1平方分米。( )
(4)把一个长方体木料锯成两个长方体,一共增加了4个面。 ( )
3.应用题。
(1)将4个棱长都是2厘米的正方体如下图摆放,露在外面的面积是多少?
(2)一个长方体的棱长总和是160厘米,它的长是12厘米,宽是5厘米。这个长方体的高是多少厘米
(3)一个长方体和一个正方体的棱长之和相等,已知长方体的长为5厘米,宽为3厘米,髙为4厘米。求正方体的棱长。
(4)一个长方体木块,它的长是12厘米,宽是10厘米,高是8厘米,现把这个长方体的木块截成一个最大的正方体。这个正方体的棱长总和是多少厘米
压轴题
填空题。
把棱长8厘米的正方体木块分割成棱长2厘米的小正方体木块,可以分割成( )块。
需要( )个棱长为3厘米的正方体,才能组成一个棱长为9厘米的正方体。
操作题。
有一块形状如下图的硬纸,把它按照虚线折叠,能不能围成一个正方体?
从一个正方体上锯下一个角(一个四面体),使得剩下部分的棱长分别为12条、13条、14条、15条,应当怎样锯?清画出示意图。
12条 13条 14条 15条
(3)用一个平面去截一个正方体,可以得到几边形?
将一个长15厘米,宽6厘米,高3厘米的长方体三等分,你有几种分法?在下图中画出来。
增加的面积各是多少?
(5)用字母标出一个正方体的各面,下图中是三个不同方位的正方体。问:字母A,B,C的对面是什么字母?
