直角三角形全等的判定[上学期]
文档属性
| 名称 | 直角三角形全等的判定[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 301.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-21 17:38:00 | ||
图片预览



文档简介
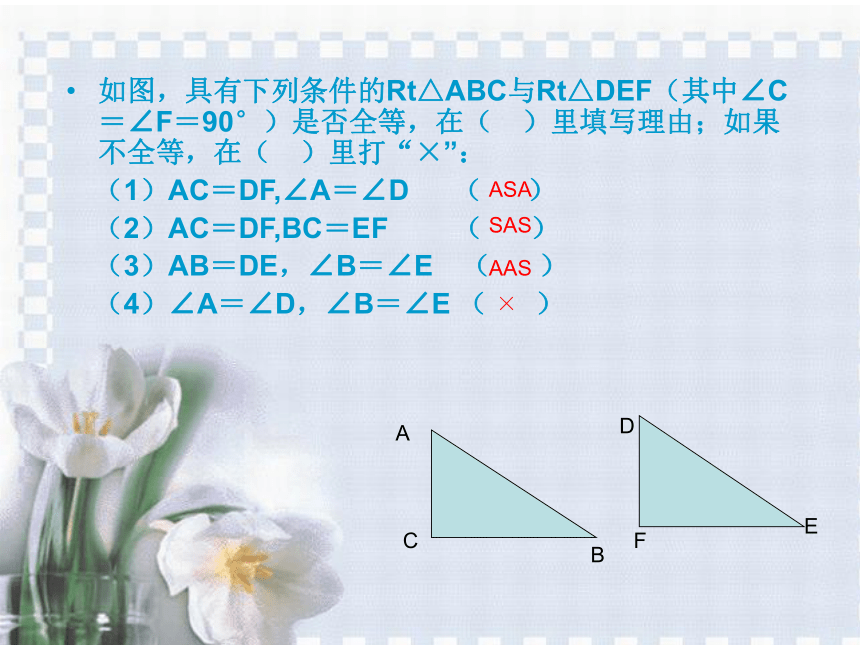
课件11张PPT。直角三角形全等的判定 北海六中 荣永彩 问题:判定一般三角形全等的方法有哪几种?若这两个三角形是直角三角形,那么这些判定方法适用吗?答:SSS,SAS,ASA,AAS如图,具有下列条件的Rt△ABC与Rt△DEF(其中∠C=∠F=90°)是否全等,在( )里填写理由;如果不全等,在( )里打“×”:
(1)AC=DF,∠A=∠D ( )
(2)AC=DF,BC=EF ( )
(3)AB=DE,∠B=∠E ( )
(4)∠A=∠D,∠B=∠E ( )
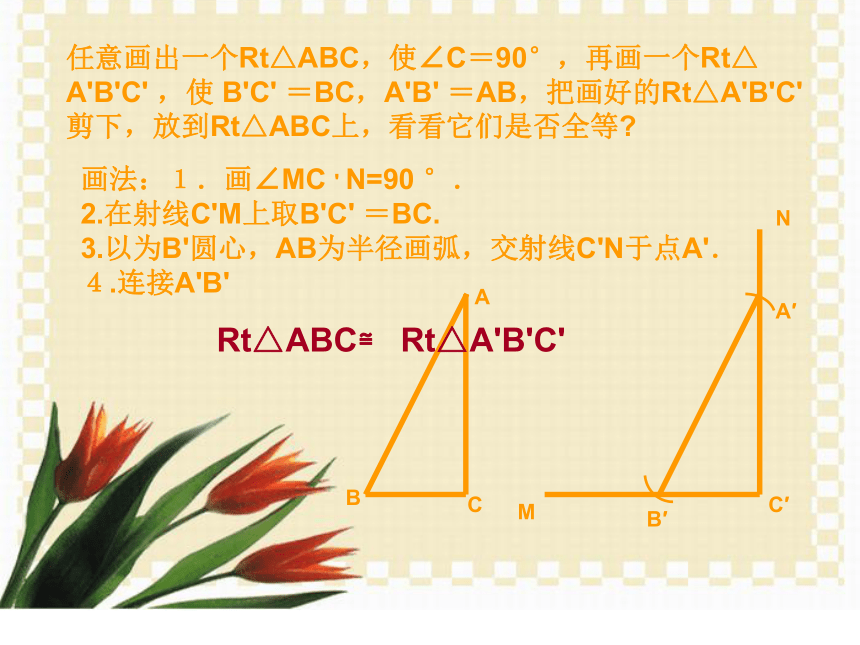
ASASASAAS×任意画出一个Rt△ABC,使∠C=90°,再画一个Rt△ A'B'C' ,使 B'C' =BC,A'B' =AB,把画好的Rt△A'B'C' 剪下,放到Rt△ABC上,看看它们是否全等?Rt△ABC≌ Rt△A'B'C' 画法:1.画∠MC ' N=90 °.
2.在射线C'M上取B'C' =BC.
3.以为B'圆心,AB为半径画弧,交射线C'N于点A'.
4.连接A'B' 两个直角三角形全等的判定:
斜边和一直角边对应相等的两个直角三角形全等
(可以简写成“斜边、直角边公理”或“HL”)
注意:“HL”是仅适用于Rt△的特殊方法。应用HL判定时,虽只有两个条件,但必须先有两个Rt△。书写格式为:
在Rt△______和Rt△______中,
∴Rt△______≌Rt△______(HL)
例1.如图,AC⊥BC,BD⊥AD,AC=BD.求证:BC=AD.
证明:∵ AC⊥BC,BD⊥AD
∴∠C=∠D=90°
在Rt△ABC 与Rt△BAD 中
AB=BA
AC=BD
∴ Rt△ABC≌ Rt△BAD(HL)
选择题
1.使两个直角三角形全等的条件是( )
2.如图,AD⊥BE,垂足C是BE的中点,AB=DE,若要证
△ABC≌ △DEC,可以根据( )
错了不对恭喜你,答对了再试一下(A)一个锐角对应相等(B)两个锐角对应相等(C)一条边对应相等(D)斜边和一条直角边对应相等
(A)边边边公理( D )边角边公理(C)角边角公理( B )斜边、直角边公理错了再试一下不对恭喜你,答对了如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别沿着两条直线行走,并同时到达D、E 两地。DA⊥AB,EB⊥AB. D、E与路段AB的距离相等吗?为什么?
证明∵ DA⊥AB,EB⊥AB
∴∠A=∠B=90°
在Rt△ACD与 Rt△BCE 中
AC=BC
CD=CE
∴ Rt△ACD ≌Rt△BCE(HL)
∴AD=BE
即D、E与路段AB的距离相等.
已知:如图,在△ABC和△A′B′C′中,CD、C′D′分别是高,并且AC=A′C′,CD=C′D′,∠ACB=∠A′C′B′。
求证:△ABC≌△A′B′C′
证明:∵ CD、C′D′分别是高
∴ ∠ADC= ∠A′D′C′=90°
在Rt△ ADC与Rt△ A′D′C′中
AC=A′C′
CD=C′D′
∴ Rt△ ADC=Rt△ A′D′C′(HL)
∴ ∠A =∠A′
在△ABC与△A′B′C′中
∠A =∠A′
AC=A′C′
∠ACB=∠A′C′B′
∴ △ABC≌△A′B′C′(ASA) 反思小结:谈谈你在这节课的收获.1.直角三角形全等的判定方法有五项依据:“SAS”、“ASA”、“ AAS”、“SSS”“HL”其中,“HL”公理只适用于判定直角三角形全等。
2.使用“HL”公理时,必须先得出两个直角三角形,然后证明斜边和一直角边对应相等。
再见!布置作业:
教材P104 7 、 8
(1)AC=DF,∠A=∠D ( )
(2)AC=DF,BC=EF ( )
(3)AB=DE,∠B=∠E ( )
(4)∠A=∠D,∠B=∠E ( )
ASASASAAS×任意画出一个Rt△ABC,使∠C=90°,再画一个Rt△ A'B'C' ,使 B'C' =BC,A'B' =AB,把画好的Rt△A'B'C' 剪下,放到Rt△ABC上,看看它们是否全等?Rt△ABC≌ Rt△A'B'C' 画法:1.画∠MC ' N=90 °.
2.在射线C'M上取B'C' =BC.
3.以为B'圆心,AB为半径画弧,交射线C'N于点A'.
4.连接A'B' 两个直角三角形全等的判定:
斜边和一直角边对应相等的两个直角三角形全等
(可以简写成“斜边、直角边公理”或“HL”)
注意:“HL”是仅适用于Rt△的特殊方法。应用HL判定时,虽只有两个条件,但必须先有两个Rt△。书写格式为:
在Rt△______和Rt△______中,
∴Rt△______≌Rt△______(HL)
例1.如图,AC⊥BC,BD⊥AD,AC=BD.求证:BC=AD.
证明:∵ AC⊥BC,BD⊥AD
∴∠C=∠D=90°
在Rt△ABC 与Rt△BAD 中
AB=BA
AC=BD
∴ Rt△ABC≌ Rt△BAD(HL)
选择题
1.使两个直角三角形全等的条件是( )
2.如图,AD⊥BE,垂足C是BE的中点,AB=DE,若要证
△ABC≌ △DEC,可以根据( )
错了不对恭喜你,答对了再试一下(A)一个锐角对应相等(B)两个锐角对应相等(C)一条边对应相等(D)斜边和一条直角边对应相等
(A)边边边公理( D )边角边公理(C)角边角公理( B )斜边、直角边公理错了再试一下不对恭喜你,答对了如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别沿着两条直线行走,并同时到达D、E 两地。DA⊥AB,EB⊥AB. D、E与路段AB的距离相等吗?为什么?
证明∵ DA⊥AB,EB⊥AB
∴∠A=∠B=90°
在Rt△ACD与 Rt△BCE 中
AC=BC
CD=CE
∴ Rt△ACD ≌Rt△BCE(HL)
∴AD=BE
即D、E与路段AB的距离相等.
已知:如图,在△ABC和△A′B′C′中,CD、C′D′分别是高,并且AC=A′C′,CD=C′D′,∠ACB=∠A′C′B′。
求证:△ABC≌△A′B′C′
证明:∵ CD、C′D′分别是高
∴ ∠ADC= ∠A′D′C′=90°
在Rt△ ADC与Rt△ A′D′C′中
AC=A′C′
CD=C′D′
∴ Rt△ ADC=Rt△ A′D′C′(HL)
∴ ∠A =∠A′
在△ABC与△A′B′C′中
∠A =∠A′
AC=A′C′
∠ACB=∠A′C′B′
∴ △ABC≌△A′B′C′(ASA) 反思小结:谈谈你在这节课的收获.1.直角三角形全等的判定方法有五项依据:“SAS”、“ASA”、“ AAS”、“SSS”“HL”其中,“HL”公理只适用于判定直角三角形全等。
2.使用“HL”公理时,必须先得出两个直角三角形,然后证明斜边和一直角边对应相等。
再见!布置作业:
教材P104 7 、 8
