2023- 2024学年沪科版八年级数学上册12.4综合与实践一次函数模型的应用 课堂同步练习 (含解析)
文档属性
| 名称 | 2023- 2024学年沪科版八年级数学上册12.4综合与实践一次函数模型的应用 课堂同步练习 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 134.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-05 17:32:31 | ||
图片预览




文档简介
2023- 2024学年沪科版八年级数学上册课堂同步练习
第12章 一次函数
12.4 综合与实践 一次函数模型的应用
1.对个人发表文章、出版图书所获稿费的纳税计算方法是y=
其中y表示稿费为x元时应缴纳的税额.若小明的爸爸取得一笔稿费,缴纳个人所得税后,得到13 320元,那么这笔稿费是( )
A.17 500元 B.15 500元
C.15 000元 D.12 000元
2.小明从家步行到学校需走的路程为1 800米.图中的折线O→A→B反映了小明从家步行到学校所走的路程s(米)与时间t(分钟)的函数关系,根据图象提供的信息,当小明从家出发去学校步行15分钟时,到学校还需步行 米.
3.如图,某品牌自行车每节链条的长度为2.5 cm,交叉重叠部分的圆的直径为0.8 cm.
(1)观察图形,填写表格;
链条节数x 1 2 3 4 …
链条长度y(cm) 2.5 4.2 5.9 …
(2)请你写出y与x之间的函数表达式;
(3)如果一辆自行车的链条(两端不相连)共由40节链条组成,那么链条的总长度是多少
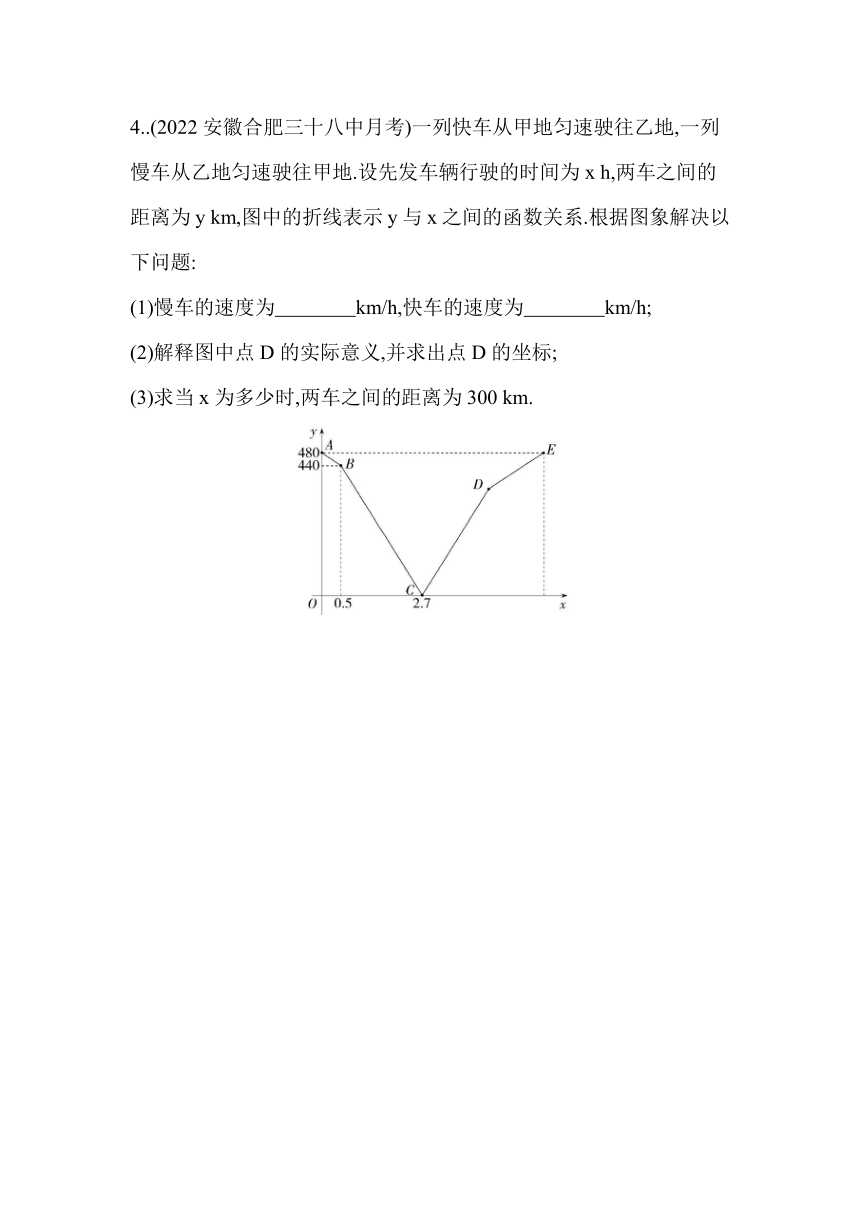
4..(2022安徽合肥三十八中月考)一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为x h,两车之间的距离为y km,图中的折线表示y与x之间的函数关系.根据图象解决以下问题:
(1)慢车的速度为 km/h,快车的速度为 km/h;
(2)解释图中点D的实际意义,并求出点D的坐标;
(3)求当x为多少时,两车之间的距离为300 km.
5. 近些年中国不负众望,国防能力得到了快速发展,为了纪念这些成就,国家发行了《中国“神舟”飞船首飞成功纪念》纪念邮票和《中国空间站》纪念邮票等.某校团委对学生进行了“国防知识竞答活动”,并决定购买一批《中国“神舟”飞船首飞成功纪念》纪念邮票和《中国空间站》纪念邮票作为奖品表彰在这次活动中成绩优异的同学,已知《中国“神舟”飞船首飞成功纪念》纪念邮票每套价格为75元,《中国空间站》纪念邮票每套价格为28元.
(1)若购买《中国“神舟”飞船首飞成功纪念》纪念邮票和《中国空间站》纪念邮票的总套数为50,且共花费2 810元,则本次购买的《中国“神舟”飞船首飞成功纪念》纪念邮票和《中国空间站》纪念邮票各多少套
(2)新学期学校计划采购上述两种奖品共100套,要求《中国“神舟”飞船首飞成功纪念》纪念邮票的套数不少于《中国空间站》纪念邮票套数的三分之一,则如何采购才能使总费用最少 最少费用是多少
6. 七年级学生梁香练习100米短跑,训练时间与100米短跑成绩记录如下:
时间(月) 1 2 3 4
成绩(秒) 15.6 15.4 15.2 15.0
(1)请你利用合适的函数模型求出梁香同学的100米短跑成绩y(秒)与训练时间x(月)之间的表达式;
(2)用所求出的函数表达式预测梁香同学训练半年(6个月)的100米短跑成绩;
(3)能用所求出的函数表达式预测梁香同学训练3年的100米短跑成绩吗 说明你的理由.
7.【国防技能学习教育】周末,某校团委组织部分优秀团员到国防教育基地开展驾驶冲锋舟训练.其中,甲、乙两组分别乘不同的冲锋舟同时从A地匀速行驶前往B地,甲组到达B地后立即沿原路匀速返回A地,图中的折线OMC表示甲组同学乘冲锋舟离A地的距离y(千米)与所用时间x(分钟)之间的函数关系,线段ON表示乙组同学乘冲锋舟离A地的距离y(千米)与所用时间x(分钟)之间的函数关系.
根据图象解答下列问题:
(1)A,B两地之间的距离为 千米,线段OM对应的函数关系式为 ,线段MC对应的函数关系式为 ,线段ON对应的函数关系式为 ;
(2)求图中线段ON和MC的交点D的坐标;
(3)直接写出整个行驶过程中,甲、乙两组同学所乘坐的冲锋舟之间的距离为5千米时,对应的行驶时间x的值.
8.(2022山东东营中考,23,★★☆)为满足顾客的购物需求,某水果店计划购进甲、乙两种水果进行销售.经了解,甲水果的进价比乙水果的进价低20%,水果店用1 000元购进甲种水果比用1 200元购进乙种水果的质量多10千克,已知甲,乙两种水果的售价分别为6元/千克和8元/千克.
(1)求甲、乙两种水果的进价分别是多少;
(2)若水果店购进这两种水果共150千克,其中甲种水果的质量不低于乙种水果质量的2倍,则水果店应如何进货才能获得最大利润 最大利润是多少
9.【新情境·乡村振兴】(2022贵州黔西南州中考,24,★★☆)某乡镇新打造的“田园风光”景区今年计划改造一片绿化地,种植A、B两种花卉,已知3盆A种花卉和4盆B种花卉的种植费用为330元,4盆A种花卉和3盆B种花卉的种植费用为300元.
(1)每盆A种花卉和每盆B种花卉的种植费用各是多少元
(2)若该景区今年计划种植A、B两种花卉共400盆,相关资料表明:A、B两种花卉的成活率分别为70%和90%,景区明年要将枯死的花卉补上相同的新花卉,但这两种花卉在明年共补的盆数不多于80盆,应如何安排这两种花卉的种植数量,才能使今年该项的种植费用最低 并求出最低费用.
10.(2022安徽亳州涡阳期中,22,★★☆)A、B两地相距60 km,甲从A地去往B地,乙从B地去往A地(如图1),图2中l1、l2分别表示甲、乙两人到B地的距离y(km)与甲出发时间x(h)的函数关系.
(1)根据图象,求乙的行驶速度;
(2)解释交点A的实际意义;
(3)求甲出发多长时间时,两人之间恰好相距5 km.
图1
图2
11.【主题教育·国家安全】【应用意识】电影《长津湖》以抗美援朝战争中的第二次战役中的长津湖战役为背景,讲述了一段波澜壮阔的历史.中国人民志愿军赴朝作战,在极寒严酷环境下,东线作战部队凭着钢铁意志和英勇无畏的战斗精神一路追击,奋勇杀敌,扭转战场态势,打出了军威国威.某中学为了培养学生的爱国主义情怀,组织师生共60人进行观影活动,电影票的价格如下表所示(教师按成人票价购票):
会员价 /(元/张) 普通票价
成人票价/(元/张) 学生票价/(元/张)
45 80 60
若师生均购买普通票,则共需3 800元.
(1)求参加观影活动的教师和学生分别有多少人;
(2)由于部分学生持有会员卡(会员卡仅限本人使用),所以有会员卡的学生享受会员价,设有会员卡的学生共x人,购买电影票的总费用为y元,若有会员卡的学生人数不超过没有会员卡的学生人数的2倍,求y的最小值.
12.【项目式学习试题】【模型观念】某景区内的环形路是边长为800米的正方形ABCD,如图所示.现有1号、2号两辆游览车分别从出口A和景点C同时出发,1号车顺时针、2号车逆时针沿环形路连续循环行驶,供游客随时免费乘车(上、下车的时间忽略不计),两车速度均为200米/分钟.
探究 设行驶时间为t分钟.
(1)当0≤t≤8时,分别写出1号车、2号车在左半环线离出口A的路程y1(米)、y2(米)与t(分钟)的函数关系式,并求出当两车相距的路程是400米时,t的值;
(2)t为何值时,1号车第三次恰好经过景点C 并直接写出这一段时间内它与2号车相遇的次数.
发现 如图②,游客甲在BC上的一点K(不与点B,C重合)处候车,准备乘车到出口A.设CK=x米.
情况一:若他刚好错过2号车,便搭乘即将到来的1号车;
情况二:若他刚好错过1号车,便搭乘即将到来的2号车.
比较哪种情况用时较多.(含候车时间)
决策 已知游客乙在DA上从D向出口A走去,步行的速度是50米/分钟.当行进到DA上一点P(不与点D,A重合)时,刚好与2号车迎面相遇.
(1)他发现,乘1号车会比乘2号车到出口A用时少,请你简要说明理由;
(2)设PA=s(0图①
图②
答案全解全析
1.C 根据题意可得x(1-20%)×20%×(1-30%)=x-13 320,整理得0.112x=x-13 320,所以0.888x=13 320,所以x=15 000,即这笔稿费是15 000元.
2.答案 350
解析 当8≤t≤20时,设s=kt+b(k≠0),将(8,960),(20,1 800)代入s=kt+b,得解得∴当8≤t≤20时,s=70t+400.
当t=15时,s=1 450,
∵1 800-1 450=350(米),
∴当小明从家出发去学校步行15分钟时,到学校还需步行350米.
3.解析 (1)7.6.(表格略)
(2)根据题意,得y=2.5+(2.5-0.8)(x-1)=1.7x+0.8,
∴y与x之间的函数表达式为y=1.7x+0.8.
(3)当x=40时,y=1.7×40+0.8=68.8(cm).
答:链条的总长度是68.8 cm.
4.解析 (1)80;120.
(2)点D的实际意义是快车到达乙地.
∵快车走完全程所需时间为480÷120=4(h),∴点D的横坐标为4.5,纵坐标为(80+120)×(4.5-2.7)=360,即点D(4.5,360).
(3)由题意,可知两车行驶的过程中有两次两车之间的距离为300 km,
相遇前:(80+120)×(x-0.5)=440-300,解得x=1.2;
相遇后:(80+120)×(x-2.7)=300,解得x=4.2,
故x=1.2或4.2时,两车之间的距离为300 km.
5.解析 (1)设购买《中国“神舟”飞船首飞成功纪念》纪念邮票x套,购买《中国空间站》纪念邮票y套,根据题意可得解得
∴购买《中国“神舟”飞船首飞成功纪念》纪念邮票30套,购买《中国空间站》纪念邮票20套.
(2)设购买《中国“神舟”飞船首飞成功纪念》纪念邮票m套,总费用为w元,则购买《中国空间站》纪念邮票(100-m)套,
根据题意可知,w=75m+28(100-m)=47m+2 800.
∵《中国“神舟”飞船首飞成功纪念》纪念邮票的套数不少于《中国空间站》纪念邮票套数的三分之一,
∴m≥(100-m),解得m≥25.
∵47>0,∴w随m的增大而增大,
∴当m=25时,w有最小值,为47×25+2 800=3 975(元).100-m=75.
∴当购买《中国“神舟”飞船首飞成功纪念》纪念邮票25套,购买《中国空间站》纪念邮票75套时,总费用最少,最少费用为3 975元.
6.解析 (1)设y=kx+b(k≠0),依题意得
解得
∴y=-0.2x+15.8.把其他数对代入也成立.
(2)当x=6时,y=-0.2×6+15.8=14.6.故预测梁香同学训练半年的100米短跑成绩为14.6秒.
(3)不能.因为短跑的成绩在短时间内可能呈某种趋势,但在较长的时间内,受自身的发展极限的限制,不会一直提高.
7.解析 (1)由题图可知,A,B两地之间的距离为20千米,
设线段OM对应的函数关系式为y=kx(k≠0),把M(24,20)代入得24k=20,解得k=,
∴线段OM对应的函数关系式为y=x(0≤x≤24);设线段MC对应的函数关系式为y=k'x+b(k'≠0),把M(24,20),C(48,0)代入得解得
∴线段MC对应的函数关系式为y=-x+40(24≤x≤48);
设线段ON对应的函数关系式为y=tx(t≠0),把N(40,20)代入得40t=20,解得t=,
∴线段ON对应的函数关系式为y=x(0≤x≤40).
(2)联立解得∴点D的坐标为(30,15).
(3)当x-x=5时,解得x=15,
当-x+40-x=5时,解得x=,
当x-=5时,解得x=,
∴甲、乙两组同学所乘坐的冲锋舟之间的距离为5千米时,对应的行驶时间x的值为15或或.
8.解析 (1)设乙种水果的进价为x元/千克,则甲种水果的进价为(1-20%)x元/千克,由题意得=+10,解得x=5.
经检验,x=5是原分式方程的解,且符合题意,则5×(1-20%)=4.
答:甲种水果的进价为4元/千克,乙种水果的进价为5元/千克.
(2)设购进甲种水果m千克,利润为w元,则购进乙种水果(150-m)千克,由题意得w=(6-4)m+(8-5)(150-m)=-m+450.
∵甲种水果的质量不低于乙种水果质量的2倍,
∴m≥2(150-m),解得m≥100.
∵-1<0,∴w随m的增大而减小,
∴当m=100时,w有最大值,为-100+450=350,150-m=50.
答:水果店应购进甲种水果100千克,乙种水果50千克,才能获得最大利润,最大利润为350元.
9.解析 (1)设每盆A种花卉的种植费用为x元,每盆B种花卉的种植费用为y元,根据题意,得解得
答:每盆A种花卉的种植费用为30元,每盆B种花卉的种植费用为60元.
(2)设种植A种花卉m盆,种植两种花卉的总费用为w元,则种植B种花卉(400-m)盆,
根据题意,得(1-70%)m+(1-90%)(400-m)≤80,
解得m≤200,
w=30m+60(400-m)=-30m+24 000,
∵-30<0,∴w随m的增大而减小,
∴当m=200时,w有最小值,为-30×200+24 000=18 000.400-200=200.
答:种植A、B两种花卉各200盆,能使今年该项的种植费用最低,最低费用为18 000元.
10.解析 (1)由图象可得乙的行驶速度为60÷(3.5-0.5)=20(km/h).
(2)设l1的函数解析式为y1=k1x+b1(k1≠0),
则解得
∴l1的函数解析式为y1=-30x+60.
设l2的函数解析式为y2=k2x+b2(k2≠0),
则解得
∴l2的函数解析式为y2=20x-10,
联立解得
∴点A的坐标为(1.4,18),
∴点A的实际意义是甲出发1.4 h时,甲、乙相遇,此时甲距离B地18 km.
(3)由题意可得|(-30x+60)-(20x-10)|=5,
解得x1=1.3,x2=1.5.
答:当甲出发1.3 h或1.5 h时,两人之间恰好相距5 km.
11.解析 (1)设参加观影活动的教师有m人,学生有n人,
依题意得解得
答:参加观影活动的教师有10人,学生有50人.
(2)∵有会员卡的学生有x人,∴购买普通票的学生有(50-x)人,
∴总费用y=80×10+45x+60(50-x)=-15x+3 800.
依题意得x≤2(50-x),解得x≤,
∵x为正整数,∴x的最大值为33.
∵-15<0,∴y随x的增大而减小,
∴当x=33时,y取得最小值,最小值=-15×33+3 800=3 305.
答:y的最小值为3 305.
12.解析 探究 (1)y1=200t,y2=-200t+1 600.
相遇前相距的路程为400米时,y2-y1=400,即-200t+1 600-200t=400,解得t=3.
相遇后相距的路程为400米时,y1-y2=400,即200t-(-200t+1 600)=400,解得t=5.
故当t=3或t=5时,两车相距的路程是400米.
(2)当1号车第三次恰好经过景点C时,200t=800×2+800×4×2,解得t=40.易知两车在点B、点D处相遇,故这一段时间内1号车与2号车相遇过5次.
发现 情况一用时为=分钟;
情况二用时为=分钟.
∵x>0,∴16-<16<16+,
∴情况二用时较多.
第12章 一次函数
12.4 综合与实践 一次函数模型的应用
1.对个人发表文章、出版图书所获稿费的纳税计算方法是y=
其中y表示稿费为x元时应缴纳的税额.若小明的爸爸取得一笔稿费,缴纳个人所得税后,得到13 320元,那么这笔稿费是( )
A.17 500元 B.15 500元
C.15 000元 D.12 000元
2.小明从家步行到学校需走的路程为1 800米.图中的折线O→A→B反映了小明从家步行到学校所走的路程s(米)与时间t(分钟)的函数关系,根据图象提供的信息,当小明从家出发去学校步行15分钟时,到学校还需步行 米.
3.如图,某品牌自行车每节链条的长度为2.5 cm,交叉重叠部分的圆的直径为0.8 cm.
(1)观察图形,填写表格;
链条节数x 1 2 3 4 …
链条长度y(cm) 2.5 4.2 5.9 …
(2)请你写出y与x之间的函数表达式;
(3)如果一辆自行车的链条(两端不相连)共由40节链条组成,那么链条的总长度是多少
4..(2022安徽合肥三十八中月考)一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为x h,两车之间的距离为y km,图中的折线表示y与x之间的函数关系.根据图象解决以下问题:
(1)慢车的速度为 km/h,快车的速度为 km/h;
(2)解释图中点D的实际意义,并求出点D的坐标;
(3)求当x为多少时,两车之间的距离为300 km.
5. 近些年中国不负众望,国防能力得到了快速发展,为了纪念这些成就,国家发行了《中国“神舟”飞船首飞成功纪念》纪念邮票和《中国空间站》纪念邮票等.某校团委对学生进行了“国防知识竞答活动”,并决定购买一批《中国“神舟”飞船首飞成功纪念》纪念邮票和《中国空间站》纪念邮票作为奖品表彰在这次活动中成绩优异的同学,已知《中国“神舟”飞船首飞成功纪念》纪念邮票每套价格为75元,《中国空间站》纪念邮票每套价格为28元.
(1)若购买《中国“神舟”飞船首飞成功纪念》纪念邮票和《中国空间站》纪念邮票的总套数为50,且共花费2 810元,则本次购买的《中国“神舟”飞船首飞成功纪念》纪念邮票和《中国空间站》纪念邮票各多少套
(2)新学期学校计划采购上述两种奖品共100套,要求《中国“神舟”飞船首飞成功纪念》纪念邮票的套数不少于《中国空间站》纪念邮票套数的三分之一,则如何采购才能使总费用最少 最少费用是多少
6. 七年级学生梁香练习100米短跑,训练时间与100米短跑成绩记录如下:
时间(月) 1 2 3 4
成绩(秒) 15.6 15.4 15.2 15.0
(1)请你利用合适的函数模型求出梁香同学的100米短跑成绩y(秒)与训练时间x(月)之间的表达式;
(2)用所求出的函数表达式预测梁香同学训练半年(6个月)的100米短跑成绩;
(3)能用所求出的函数表达式预测梁香同学训练3年的100米短跑成绩吗 说明你的理由.
7.【国防技能学习教育】周末,某校团委组织部分优秀团员到国防教育基地开展驾驶冲锋舟训练.其中,甲、乙两组分别乘不同的冲锋舟同时从A地匀速行驶前往B地,甲组到达B地后立即沿原路匀速返回A地,图中的折线OMC表示甲组同学乘冲锋舟离A地的距离y(千米)与所用时间x(分钟)之间的函数关系,线段ON表示乙组同学乘冲锋舟离A地的距离y(千米)与所用时间x(分钟)之间的函数关系.
根据图象解答下列问题:
(1)A,B两地之间的距离为 千米,线段OM对应的函数关系式为 ,线段MC对应的函数关系式为 ,线段ON对应的函数关系式为 ;
(2)求图中线段ON和MC的交点D的坐标;
(3)直接写出整个行驶过程中,甲、乙两组同学所乘坐的冲锋舟之间的距离为5千米时,对应的行驶时间x的值.
8.(2022山东东营中考,23,★★☆)为满足顾客的购物需求,某水果店计划购进甲、乙两种水果进行销售.经了解,甲水果的进价比乙水果的进价低20%,水果店用1 000元购进甲种水果比用1 200元购进乙种水果的质量多10千克,已知甲,乙两种水果的售价分别为6元/千克和8元/千克.
(1)求甲、乙两种水果的进价分别是多少;
(2)若水果店购进这两种水果共150千克,其中甲种水果的质量不低于乙种水果质量的2倍,则水果店应如何进货才能获得最大利润 最大利润是多少
9.【新情境·乡村振兴】(2022贵州黔西南州中考,24,★★☆)某乡镇新打造的“田园风光”景区今年计划改造一片绿化地,种植A、B两种花卉,已知3盆A种花卉和4盆B种花卉的种植费用为330元,4盆A种花卉和3盆B种花卉的种植费用为300元.
(1)每盆A种花卉和每盆B种花卉的种植费用各是多少元
(2)若该景区今年计划种植A、B两种花卉共400盆,相关资料表明:A、B两种花卉的成活率分别为70%和90%,景区明年要将枯死的花卉补上相同的新花卉,但这两种花卉在明年共补的盆数不多于80盆,应如何安排这两种花卉的种植数量,才能使今年该项的种植费用最低 并求出最低费用.
10.(2022安徽亳州涡阳期中,22,★★☆)A、B两地相距60 km,甲从A地去往B地,乙从B地去往A地(如图1),图2中l1、l2分别表示甲、乙两人到B地的距离y(km)与甲出发时间x(h)的函数关系.
(1)根据图象,求乙的行驶速度;
(2)解释交点A的实际意义;
(3)求甲出发多长时间时,两人之间恰好相距5 km.
图1
图2
11.【主题教育·国家安全】【应用意识】电影《长津湖》以抗美援朝战争中的第二次战役中的长津湖战役为背景,讲述了一段波澜壮阔的历史.中国人民志愿军赴朝作战,在极寒严酷环境下,东线作战部队凭着钢铁意志和英勇无畏的战斗精神一路追击,奋勇杀敌,扭转战场态势,打出了军威国威.某中学为了培养学生的爱国主义情怀,组织师生共60人进行观影活动,电影票的价格如下表所示(教师按成人票价购票):
会员价 /(元/张) 普通票价
成人票价/(元/张) 学生票价/(元/张)
45 80 60
若师生均购买普通票,则共需3 800元.
(1)求参加观影活动的教师和学生分别有多少人;
(2)由于部分学生持有会员卡(会员卡仅限本人使用),所以有会员卡的学生享受会员价,设有会员卡的学生共x人,购买电影票的总费用为y元,若有会员卡的学生人数不超过没有会员卡的学生人数的2倍,求y的最小值.
12.【项目式学习试题】【模型观念】某景区内的环形路是边长为800米的正方形ABCD,如图所示.现有1号、2号两辆游览车分别从出口A和景点C同时出发,1号车顺时针、2号车逆时针沿环形路连续循环行驶,供游客随时免费乘车(上、下车的时间忽略不计),两车速度均为200米/分钟.
探究 设行驶时间为t分钟.
(1)当0≤t≤8时,分别写出1号车、2号车在左半环线离出口A的路程y1(米)、y2(米)与t(分钟)的函数关系式,并求出当两车相距的路程是400米时,t的值;
(2)t为何值时,1号车第三次恰好经过景点C 并直接写出这一段时间内它与2号车相遇的次数.
发现 如图②,游客甲在BC上的一点K(不与点B,C重合)处候车,准备乘车到出口A.设CK=x米.
情况一:若他刚好错过2号车,便搭乘即将到来的1号车;
情况二:若他刚好错过1号车,便搭乘即将到来的2号车.
比较哪种情况用时较多.(含候车时间)
决策 已知游客乙在DA上从D向出口A走去,步行的速度是50米/分钟.当行进到DA上一点P(不与点D,A重合)时,刚好与2号车迎面相遇.
(1)他发现,乘1号车会比乘2号车到出口A用时少,请你简要说明理由;
(2)设PA=s(0
图②
答案全解全析
1.C 根据题意可得x(1-20%)×20%×(1-30%)=x-13 320,整理得0.112x=x-13 320,所以0.888x=13 320,所以x=15 000,即这笔稿费是15 000元.
2.答案 350
解析 当8≤t≤20时,设s=kt+b(k≠0),将(8,960),(20,1 800)代入s=kt+b,得解得∴当8≤t≤20时,s=70t+400.
当t=15时,s=1 450,
∵1 800-1 450=350(米),
∴当小明从家出发去学校步行15分钟时,到学校还需步行350米.
3.解析 (1)7.6.(表格略)
(2)根据题意,得y=2.5+(2.5-0.8)(x-1)=1.7x+0.8,
∴y与x之间的函数表达式为y=1.7x+0.8.
(3)当x=40时,y=1.7×40+0.8=68.8(cm).
答:链条的总长度是68.8 cm.
4.解析 (1)80;120.
(2)点D的实际意义是快车到达乙地.
∵快车走完全程所需时间为480÷120=4(h),∴点D的横坐标为4.5,纵坐标为(80+120)×(4.5-2.7)=360,即点D(4.5,360).
(3)由题意,可知两车行驶的过程中有两次两车之间的距离为300 km,
相遇前:(80+120)×(x-0.5)=440-300,解得x=1.2;
相遇后:(80+120)×(x-2.7)=300,解得x=4.2,
故x=1.2或4.2时,两车之间的距离为300 km.
5.解析 (1)设购买《中国“神舟”飞船首飞成功纪念》纪念邮票x套,购买《中国空间站》纪念邮票y套,根据题意可得解得
∴购买《中国“神舟”飞船首飞成功纪念》纪念邮票30套,购买《中国空间站》纪念邮票20套.
(2)设购买《中国“神舟”飞船首飞成功纪念》纪念邮票m套,总费用为w元,则购买《中国空间站》纪念邮票(100-m)套,
根据题意可知,w=75m+28(100-m)=47m+2 800.
∵《中国“神舟”飞船首飞成功纪念》纪念邮票的套数不少于《中国空间站》纪念邮票套数的三分之一,
∴m≥(100-m),解得m≥25.
∵47>0,∴w随m的增大而增大,
∴当m=25时,w有最小值,为47×25+2 800=3 975(元).100-m=75.
∴当购买《中国“神舟”飞船首飞成功纪念》纪念邮票25套,购买《中国空间站》纪念邮票75套时,总费用最少,最少费用为3 975元.
6.解析 (1)设y=kx+b(k≠0),依题意得
解得
∴y=-0.2x+15.8.把其他数对代入也成立.
(2)当x=6时,y=-0.2×6+15.8=14.6.故预测梁香同学训练半年的100米短跑成绩为14.6秒.
(3)不能.因为短跑的成绩在短时间内可能呈某种趋势,但在较长的时间内,受自身的发展极限的限制,不会一直提高.
7.解析 (1)由题图可知,A,B两地之间的距离为20千米,
设线段OM对应的函数关系式为y=kx(k≠0),把M(24,20)代入得24k=20,解得k=,
∴线段OM对应的函数关系式为y=x(0≤x≤24);设线段MC对应的函数关系式为y=k'x+b(k'≠0),把M(24,20),C(48,0)代入得解得
∴线段MC对应的函数关系式为y=-x+40(24≤x≤48);
设线段ON对应的函数关系式为y=tx(t≠0),把N(40,20)代入得40t=20,解得t=,
∴线段ON对应的函数关系式为y=x(0≤x≤40).
(2)联立解得∴点D的坐标为(30,15).
(3)当x-x=5时,解得x=15,
当-x+40-x=5时,解得x=,
当x-=5时,解得x=,
∴甲、乙两组同学所乘坐的冲锋舟之间的距离为5千米时,对应的行驶时间x的值为15或或.
8.解析 (1)设乙种水果的进价为x元/千克,则甲种水果的进价为(1-20%)x元/千克,由题意得=+10,解得x=5.
经检验,x=5是原分式方程的解,且符合题意,则5×(1-20%)=4.
答:甲种水果的进价为4元/千克,乙种水果的进价为5元/千克.
(2)设购进甲种水果m千克,利润为w元,则购进乙种水果(150-m)千克,由题意得w=(6-4)m+(8-5)(150-m)=-m+450.
∵甲种水果的质量不低于乙种水果质量的2倍,
∴m≥2(150-m),解得m≥100.
∵-1<0,∴w随m的增大而减小,
∴当m=100时,w有最大值,为-100+450=350,150-m=50.
答:水果店应购进甲种水果100千克,乙种水果50千克,才能获得最大利润,最大利润为350元.
9.解析 (1)设每盆A种花卉的种植费用为x元,每盆B种花卉的种植费用为y元,根据题意,得解得
答:每盆A种花卉的种植费用为30元,每盆B种花卉的种植费用为60元.
(2)设种植A种花卉m盆,种植两种花卉的总费用为w元,则种植B种花卉(400-m)盆,
根据题意,得(1-70%)m+(1-90%)(400-m)≤80,
解得m≤200,
w=30m+60(400-m)=-30m+24 000,
∵-30<0,∴w随m的增大而减小,
∴当m=200时,w有最小值,为-30×200+24 000=18 000.400-200=200.
答:种植A、B两种花卉各200盆,能使今年该项的种植费用最低,最低费用为18 000元.
10.解析 (1)由图象可得乙的行驶速度为60÷(3.5-0.5)=20(km/h).
(2)设l1的函数解析式为y1=k1x+b1(k1≠0),
则解得
∴l1的函数解析式为y1=-30x+60.
设l2的函数解析式为y2=k2x+b2(k2≠0),
则解得
∴l2的函数解析式为y2=20x-10,
联立解得
∴点A的坐标为(1.4,18),
∴点A的实际意义是甲出发1.4 h时,甲、乙相遇,此时甲距离B地18 km.
(3)由题意可得|(-30x+60)-(20x-10)|=5,
解得x1=1.3,x2=1.5.
答:当甲出发1.3 h或1.5 h时,两人之间恰好相距5 km.
11.解析 (1)设参加观影活动的教师有m人,学生有n人,
依题意得解得
答:参加观影活动的教师有10人,学生有50人.
(2)∵有会员卡的学生有x人,∴购买普通票的学生有(50-x)人,
∴总费用y=80×10+45x+60(50-x)=-15x+3 800.
依题意得x≤2(50-x),解得x≤,
∵x为正整数,∴x的最大值为33.
∵-15<0,∴y随x的增大而减小,
∴当x=33时,y取得最小值,最小值=-15×33+3 800=3 305.
答:y的最小值为3 305.
12.解析 探究 (1)y1=200t,y2=-200t+1 600.
相遇前相距的路程为400米时,y2-y1=400,即-200t+1 600-200t=400,解得t=3.
相遇后相距的路程为400米时,y1-y2=400,即200t-(-200t+1 600)=400,解得t=5.
故当t=3或t=5时,两车相距的路程是400米.
(2)当1号车第三次恰好经过景点C时,200t=800×2+800×4×2,解得t=40.易知两车在点B、点D处相遇,故这一段时间内1号车与2号车相遇过5次.
发现 情况一用时为=分钟;
情况二用时为=分钟.
∵x>0,∴16-<16<16+,
∴情况二用时较多.
