8.2特殊平行四边形——正方形复习课件
文档属性
| 名称 | 8.2特殊平行四边形——正方形复习课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 212.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-11-21 15:16:32 | ||
图片预览





文档简介
课件16张PPT。素养训练1.菱形的性质有哪些?
2.菱形的判定方法有哪些?
3.矩形的性质有哪些?
4.矩形的判定方法有哪些?
请任选一个问题回答:正方形 复习学习目标1、复习正方形的定义、性质及判定方法;
2、灵活运用上述知识点解决相关问题。 回忆旧知一1.正方形有哪些性质?正方形的四条边都相等,对边平行,四个角都是直角。
正方形的两条对角线相等,并且互相垂直、平分,每条对角线平分一组对角。 练习一1、正方形具有而菱形不一定具有的特征是( )
A四条边都相等 B对角线互相垂直平分
C对角线平分一组对角 D对角线相等
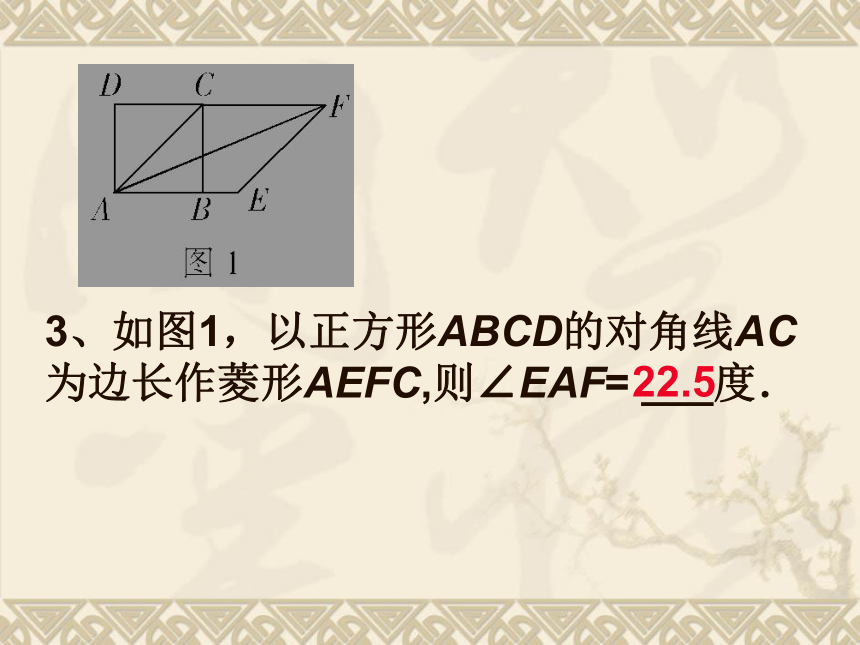
2、边长为2cm的正方形的对角线长为_______,面积为______。D3、如图1,以正方形ABCD的对角线AC为边长作菱形AEFC,则∠EAF= ___度.
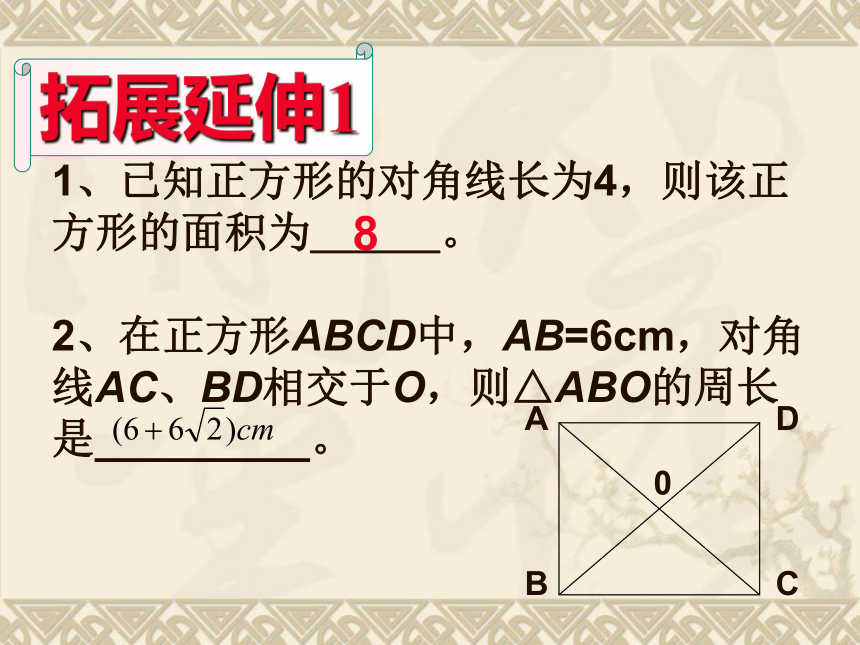
22.5拓展延伸11、已知正方形的对角线长为4,则该正方形的面积为___。
2、在正方形ABCD中,AB=6cm,对角线AC、BD相交于O,则△ABO的周长是_________。8正方形有哪些判定方法?回忆旧知二1.有一组邻边相等的矩形是正方形。
2.对角线互相垂直的矩形是正方形。
3.有一个角是直角的菱形是正方形。
4.对角线相等的菱形是正方形。 练习二1、能判定四边形是正方形的条件是( )
A.对角线相等 B.对角线互相垂直平分
C.对角线相等且垂直D.对角线相等且互相垂直平分
2、下列命题中:
①既是矩形又是菱形的四边形是正方形;
②对角线相等且互相垂直平分的四边形是正方形;
③对角线互相垂直的矩形是正方形;
④对角线相等,四条边相等的四边形是正方形,
你认为正确的有( )
A、1个 B、2个 C、3个 D、4个 DD3、如图,Rt△ABC中,∠BAC =90°, AD平分∠BAC, DE∥AC交AB于点E,DF∥AB交AC于点F,四边形AEDF是正方形吗?请说明理由.拓展延伸2 如图,在△ABC中, ∠ACB= 90°,BC的垂直平分线EF交BC于D,交AB于E,且CF=BE.
(1)求证:四边形BECF是菱形.
(2)当∠A的大小满足什么条件时,
菱形BECF是正方形?
请回答并证明你的结论. 课堂小结1.什么叫做正方形?一组邻边相等的矩形叫做正方形2.正方形有哪些性质?正方形的四条边都相等,对边平行,四个角都是直角。正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角。3.正方形有哪些判定方法?有一组邻边相等的矩形是正方形。
对角线互相垂直的矩形是正方形。
有一个角是直角的菱形是正方形。
对角线相等的菱形是正方形。 2.如图,已知 中, 平分 .
(1)四边形ADFE是菱形吗?请说明理由.
(2) 满足什么条件时,四边形ADFE是正方形?课堂检测1.已知四边形ABCD是菱形,当满足条件______时,它成为正方形。(填上你认为正确的一个条件即可) 作业巩固性作业:复习卷1-6
拓展性作业:
1.如图,矩形内有两个相邻的正方形,面积分别为4和2,那么阴影部分的面积为 . 2.如图1,在正方形ABCD中,点P是CD上一动点,连结PA,分别过点B、D作BE⊥PA、DF⊥PA,垂足为E、F。
(1)请探究BE、DF、EF这三条线段长度具有怎样的数量关系。若点P在DC的延长线上(如图2),那么这三条线段的长度之间又具有怎样的数量关系?若点P在CD的延长线上呢(如图3)?请分别直接写出结论; (2)请在(1)中的三个结论中选择一个说明理由
2.菱形的判定方法有哪些?
3.矩形的性质有哪些?
4.矩形的判定方法有哪些?
请任选一个问题回答:正方形 复习学习目标1、复习正方形的定义、性质及判定方法;
2、灵活运用上述知识点解决相关问题。 回忆旧知一1.正方形有哪些性质?正方形的四条边都相等,对边平行,四个角都是直角。
正方形的两条对角线相等,并且互相垂直、平分,每条对角线平分一组对角。 练习一1、正方形具有而菱形不一定具有的特征是( )
A四条边都相等 B对角线互相垂直平分
C对角线平分一组对角 D对角线相等
2、边长为2cm的正方形的对角线长为_______,面积为______。D3、如图1,以正方形ABCD的对角线AC为边长作菱形AEFC,则∠EAF= ___度.
22.5拓展延伸11、已知正方形的对角线长为4,则该正方形的面积为___。
2、在正方形ABCD中,AB=6cm,对角线AC、BD相交于O,则△ABO的周长是_________。8正方形有哪些判定方法?回忆旧知二1.有一组邻边相等的矩形是正方形。
2.对角线互相垂直的矩形是正方形。
3.有一个角是直角的菱形是正方形。
4.对角线相等的菱形是正方形。 练习二1、能判定四边形是正方形的条件是( )
A.对角线相等 B.对角线互相垂直平分
C.对角线相等且垂直D.对角线相等且互相垂直平分
2、下列命题中:
①既是矩形又是菱形的四边形是正方形;
②对角线相等且互相垂直平分的四边形是正方形;
③对角线互相垂直的矩形是正方形;
④对角线相等,四条边相等的四边形是正方形,
你认为正确的有( )
A、1个 B、2个 C、3个 D、4个 DD3、如图,Rt△ABC中,∠BAC =90°, AD平分∠BAC, DE∥AC交AB于点E,DF∥AB交AC于点F,四边形AEDF是正方形吗?请说明理由.拓展延伸2 如图,在△ABC中, ∠ACB= 90°,BC的垂直平分线EF交BC于D,交AB于E,且CF=BE.
(1)求证:四边形BECF是菱形.
(2)当∠A的大小满足什么条件时,
菱形BECF是正方形?
请回答并证明你的结论. 课堂小结1.什么叫做正方形?一组邻边相等的矩形叫做正方形2.正方形有哪些性质?正方形的四条边都相等,对边平行,四个角都是直角。正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角。3.正方形有哪些判定方法?有一组邻边相等的矩形是正方形。
对角线互相垂直的矩形是正方形。
有一个角是直角的菱形是正方形。
对角线相等的菱形是正方形。 2.如图,已知 中, 平分 .
(1)四边形ADFE是菱形吗?请说明理由.
(2) 满足什么条件时,四边形ADFE是正方形?课堂检测1.已知四边形ABCD是菱形,当满足条件______时,它成为正方形。(填上你认为正确的一个条件即可) 作业巩固性作业:复习卷1-6
拓展性作业:
1.如图,矩形内有两个相邻的正方形,面积分别为4和2,那么阴影部分的面积为 . 2.如图1,在正方形ABCD中,点P是CD上一动点,连结PA,分别过点B、D作BE⊥PA、DF⊥PA,垂足为E、F。
(1)请探究BE、DF、EF这三条线段长度具有怎样的数量关系。若点P在DC的延长线上(如图2),那么这三条线段的长度之间又具有怎样的数量关系?若点P在CD的延长线上呢(如图3)?请分别直接写出结论; (2)请在(1)中的三个结论中选择一个说明理由
