数学人教A版(2019)必修第一册5.5.1.1两角差的余弦公式 课件(共27张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.5.1.1两角差的余弦公式 课件(共27张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-04 17:36:52 | ||
图片预览







文档简介
(共27张PPT)
第五章 三角函数
5.5.1.1 两角差的余弦公式
高中数学/人教A版/必修一
某城市的电视发射塔建在市郊的一座小山上.如图所示, 在地平面上有一点A,测得A,C两点间距离约为60米,从A观测电视发射塔的视角(∠CAD)约为45°, ∠CAB=15°.求这座电视发射塔的高度.
B
D
A
C
60
45°
15°
1
情境导入
对于30°,45°,60°等特殊角的三角函数值可以直接写出,利用诱导公式还可进一步求出150°,210°,315°等角的三角函数值.
我们希望再引进一些公式,能够求更多的非特殊角的三角函数值,同时也为三角恒等变换提供理论依据.
1
两角差的余弦公式
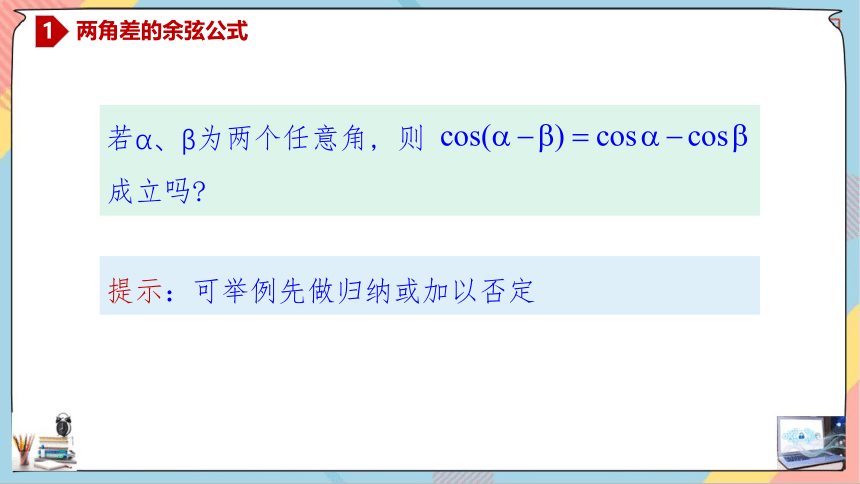
若α、β为两个任意角, 则
成立吗
1
两角差的余弦公式
提示:可举例先做归纳或加以否定
1
两角差的余弦公式
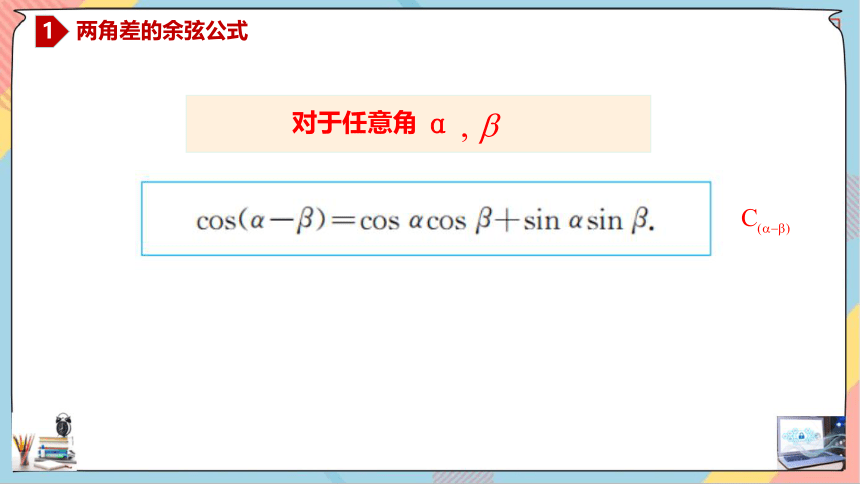
对于任意角
1
两角差的余弦公式
B
练一练
例1. 利用两角差的余弦公式求cos15°的值.
法1:
2
两角差的余弦公式的应用
法2:
C
练一练
例2.已知
是第三象限角 ,求 的值.
解:
由
得
2
两角差的余弦公式的应用
又由
是第三象限角,得
所以
解:
练一练
例3.已知
求
由
得
由
得
2
两角差的余弦公式的应用
解:
已知 且 求 的值
练一练
A
练一练
C
练一练
练一练
5.已知 为锐角,求
练一练
6.已知 求
练一练
课堂小结
一、本节课学习的新知识
两角差的余弦公式
两角差的余弦公式的应用
二、本节课提升的核心素养
数学建模
课堂小结
数学运算
逻辑推理
三、本节课训练的数学思想方法
数形结合
课堂小结
构造思想
类比思想
第五章 三角函数
5.5.1.1 两角差的余弦公式
高中数学/人教A版/必修一
某城市的电视发射塔建在市郊的一座小山上.如图所示, 在地平面上有一点A,测得A,C两点间距离约为60米,从A观测电视发射塔的视角(∠CAD)约为45°, ∠CAB=15°.求这座电视发射塔的高度.
B
D
A
C
60
45°
15°
1
情境导入
对于30°,45°,60°等特殊角的三角函数值可以直接写出,利用诱导公式还可进一步求出150°,210°,315°等角的三角函数值.
我们希望再引进一些公式,能够求更多的非特殊角的三角函数值,同时也为三角恒等变换提供理论依据.
1
两角差的余弦公式
若α、β为两个任意角, 则
成立吗
1
两角差的余弦公式
提示:可举例先做归纳或加以否定
1
两角差的余弦公式
对于任意角
1
两角差的余弦公式
B
练一练
例1. 利用两角差的余弦公式求cos15°的值.
法1:
2
两角差的余弦公式的应用
法2:
C
练一练
例2.已知
是第三象限角 ,求 的值.
解:
由
得
2
两角差的余弦公式的应用
又由
是第三象限角,得
所以
解:
练一练
例3.已知
求
由
得
由
得
2
两角差的余弦公式的应用
解:
已知 且 求 的值
练一练
A
练一练
C
练一练
练一练
5.已知 为锐角,求
练一练
6.已知 求
练一练
课堂小结
一、本节课学习的新知识
两角差的余弦公式
两角差的余弦公式的应用
二、本节课提升的核心素养
数学建模
课堂小结
数学运算
逻辑推理
三、本节课训练的数学思想方法
数形结合
课堂小结
构造思想
类比思想
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
