19.2.1 矩形(一)[下学期]
文档属性
| 名称 | 19.2.1 矩形(一)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 887.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-05-10 00:00:00 | ||
图片预览




文档简介
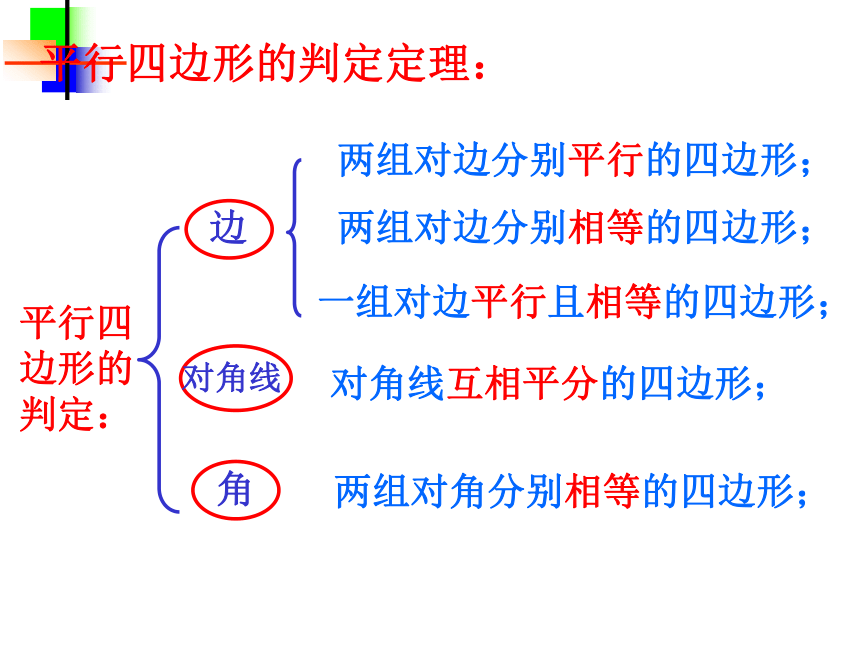
课件23张PPT。19.2特殊的平行四边形1-1八年级 数学第十九章 四边形两组对边分别平行的四边形是平行四边形平行四边形的性质:平行四边形的对边平行;平行四边形的对边相等;平行四边形的对角相等;平行四边形的邻角互补;平行四边形的对角线互相平分; 温故知新平行四边形的判定:两组对边分别平行的四边形;两组对边分别相等的四边形;两组对角分别相等的四边形;对角线互相平分的四边形;一组对边平行且相等的四边形;平行四边形的判定定理:定义:把连接三角形两边中点的线段叫做三角形的中位线 温故知新第十九章 四边形一个角是
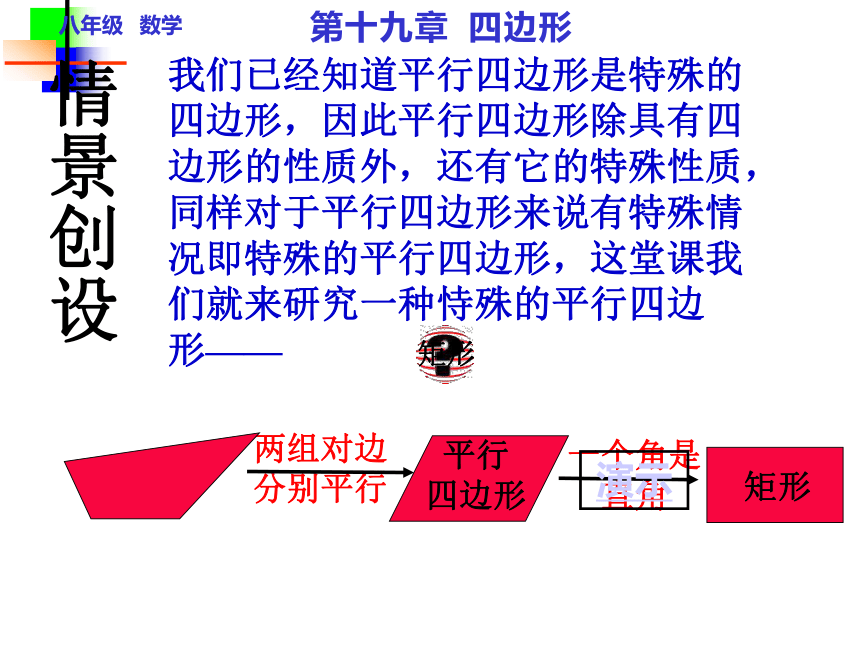
直角两组对边
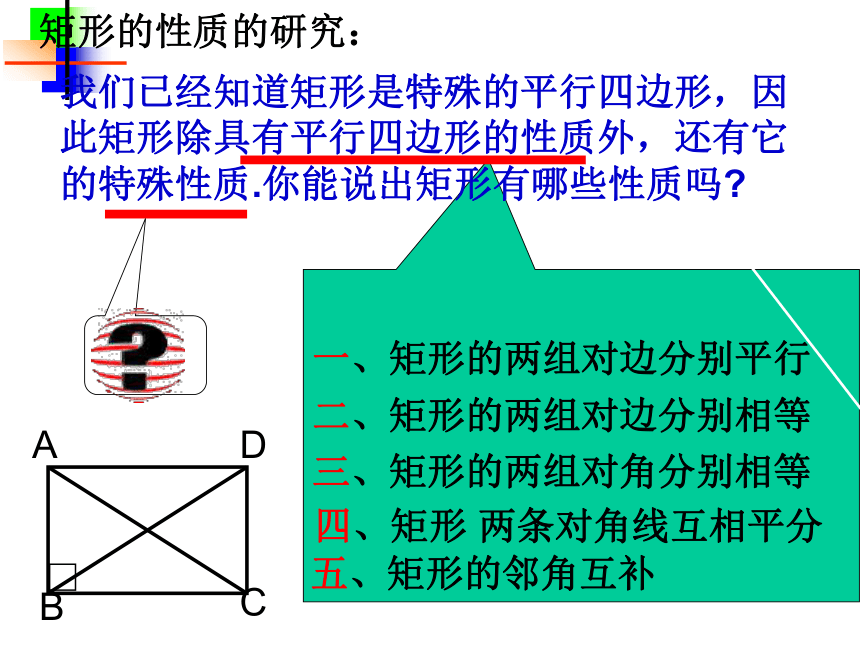
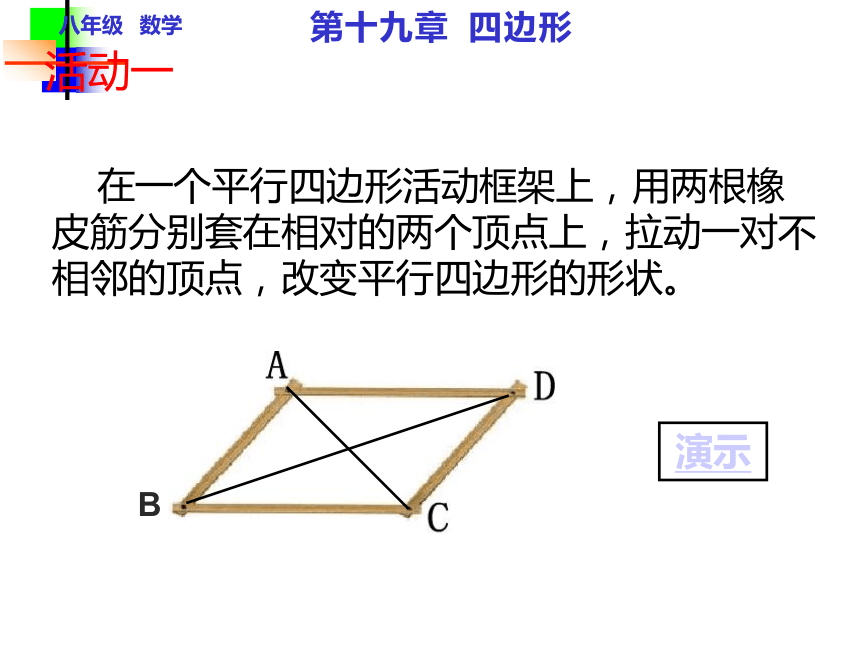
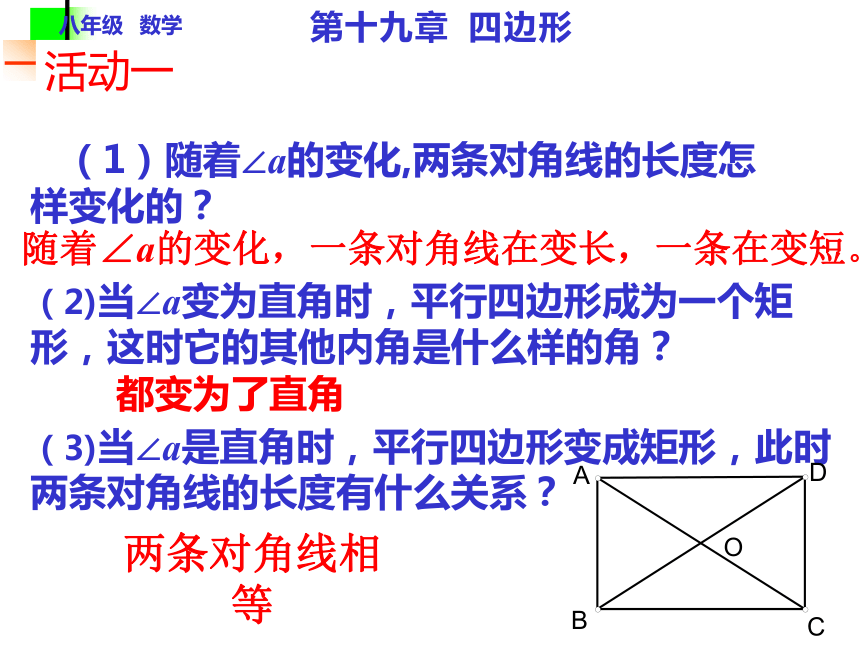
分别平行矩形情景创设我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说有特殊情况即特殊的平行四边形,这堂课我们就来研究一种恃殊的平行四边形—— 矩形演示八年级 数学第十九章 四边形八年级 数学矩形定义第十九章 四边形 我们生活中充满了矩形这种几何图形,教室里的黑板,门窗,课桌的桌面,信封明信片等都是矩形的形状,你知道什么是矩形吗? 你是否了解这种几何图形的性质呢?定义:有一个角是直角的平行四边形叫做矩形矩形的性质的研究:我们已经知道矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有它的特殊性质.你能说出矩形有哪些性质吗?四、矩形 两条对角线互相平分三、矩形的两组对角分别相等二、矩形的两组对边分别相等一、矩形的两组对边分别平行五、矩形的邻角互补八年级 数学活动一第十九章 四边形 在一个平行四边形活动框架上,用两根橡皮筋分别套在相对的两个顶点上,拉动一对不相邻的顶点,改变平行四边形的形状。演示 (1)随着∠a的变化,两条对角线的长度怎
样变化的?(2)当∠a变为直角时,平行四边形成为一个矩形,这时它的其他内角是什么样的角?(3)当∠a是直角时,平行四边形变成矩形,此时
两条对角线的长度有什么关系?随着∠a的变化,一条对角线在变长,一条在变短。都变为了直角两条对角线相等八年级 数学活动一第十九章 四边形八年级 数学第十九章 四边形综上所述可得矩形的特殊性质:矩形的四个角都是直角.矩形的两条对角线相等且互相平分.矩形的对边平行且相等.矩形本身是平行四边形,所以它具有平行四边形的所有性质边对角线角矩形的性质:矩形对边平行且相等;矩形的四个角都是直角;矩形的对角线相等且平分;八年级 数学第十九章 四边形定理:矩形的四个角都是直角.已知:如图,四边形ABCD是矩形.分析:由矩形的定义,利用对角相等,邻角互补可使问题得证.证明:∵ 四边形ABCD是矩形,∴∠A=900,四边形ABCD是平行四边形.∴∠C=∠A=900,
∠B=1800-∠A=900,
∠D=1800-∠A=900.求证:∠A=∠B=∠C=∠D=900.∴四边形ABCD是矩形.八年级 数学矩形的性质第十九章 四边形定理:矩形的两条对角线相等.已知:AC,BD是矩形ABCD的两条对角线.求证: AC=BD.证明:∵ 四边形ABCD是矩形,∴AB=DC,∠ABC=∠DCB=900.分析:根据矩形的性质性质,可转化为全等三角形(SAS)来证明.∵BC=CB,∴△ABC≌△DCB(SAS).∴AC=DB.八年级 数学矩形的性质第十九章 四边形设矩形的对角线AC与BD交于点E,那么,BE是Rt△ABC中一条怎样的特殊线段? 它与AC有什么大小关系?为什么?由此可得推论:
直角三角形斜边上的中线等于斜边的一半BE是Rt△ABC中斜边AC上的中线. BE等于AC的一半.∵ AC=BD,BE=DE,议一议:八年级 数学第十九章 四边形推论:直角三角形斜边上的中线等于斜边的一半.证明:延长CD到E使DE=CD,
连结AE、BE.∵AD = BD , DE =CD
∴四边形ACBE是平行四边形E?八年级 数学第十九章 四边形ODCBA相等的线段:相等的角:∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC ∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB等腰三角形有:△OAB △ OBC △OCD △OAD直角三角形有:Rt△ABC Rt△BCD Rt△CDA Rt△DAB全等三角形有:Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB
△OAB≌△OCD △OAD≌△OCB已知四边形ABCD是矩形思考:矩形ABCD是轴对称图形吗?它的对称轴有几条?矩形是中心对称图形吗?对称中心是?ABCDEFGH.八年级 数学第十九章 四边形矩形性质的应用 已知:如图,AC,BD是矩形ABCD的两条对线,AC,BD相交于点O,∠AOD=1200,AB=2.5cm.求矩形对角线的长.解:∵四边形ABCD是矩形,∴BD=2AB=2×2.5=5(cm).∴AC=BD,且∵∠DAB=900,∵∠AOD=1200,八年级 数学第十九章 四边形例2、例3教案.学案八年级 数学第十九章 四边形练一练:书本P104:练习3练习:如图四边形ABCD中,∠ABC=∠ADC=900,E是AC中点,EF平分∠BED交BD于点F,
(1)猜想EF与BD具有怎样的关系?
(2)试证明你的猜想。生活中的数学 给你一根足够长的绳子,你能检查教室的门窗或你的桌子是不是矩形吗?你怎样检查?解释其中的道理。八年级 数学学以致用第十九章 四边形四边形ABCD是矩形
若已知AB=8㎝,AD=6㎝,
则AC= ㎝ OB= ㎝
若已知∠CAB=40°,则∠OCB=
∠OBA= ∠AOB= ∠AOD=
若已知AC=10㎝,BC=6㎝,则矩形的周长= ㎝
矩形的面积= ㎝2
4 若已知 ∠DOC=120°,AD=6㎝,则AC= ㎝550°10100°40°12482880°练一练八年级 数学第十九章 四边形学习了本节课你有哪些收获?
直角两组对边
分别平行矩形情景创设我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说有特殊情况即特殊的平行四边形,这堂课我们就来研究一种恃殊的平行四边形—— 矩形演示八年级 数学第十九章 四边形八年级 数学矩形定义第十九章 四边形 我们生活中充满了矩形这种几何图形,教室里的黑板,门窗,课桌的桌面,信封明信片等都是矩形的形状,你知道什么是矩形吗? 你是否了解这种几何图形的性质呢?定义:有一个角是直角的平行四边形叫做矩形矩形的性质的研究:我们已经知道矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有它的特殊性质.你能说出矩形有哪些性质吗?四、矩形 两条对角线互相平分三、矩形的两组对角分别相等二、矩形的两组对边分别相等一、矩形的两组对边分别平行五、矩形的邻角互补八年级 数学活动一第十九章 四边形 在一个平行四边形活动框架上,用两根橡皮筋分别套在相对的两个顶点上,拉动一对不相邻的顶点,改变平行四边形的形状。演示 (1)随着∠a的变化,两条对角线的长度怎
样变化的?(2)当∠a变为直角时,平行四边形成为一个矩形,这时它的其他内角是什么样的角?(3)当∠a是直角时,平行四边形变成矩形,此时
两条对角线的长度有什么关系?随着∠a的变化,一条对角线在变长,一条在变短。都变为了直角两条对角线相等八年级 数学活动一第十九章 四边形八年级 数学第十九章 四边形综上所述可得矩形的特殊性质:矩形的四个角都是直角.矩形的两条对角线相等且互相平分.矩形的对边平行且相等.矩形本身是平行四边形,所以它具有平行四边形的所有性质边对角线角矩形的性质:矩形对边平行且相等;矩形的四个角都是直角;矩形的对角线相等且平分;八年级 数学第十九章 四边形定理:矩形的四个角都是直角.已知:如图,四边形ABCD是矩形.分析:由矩形的定义,利用对角相等,邻角互补可使问题得证.证明:∵ 四边形ABCD是矩形,∴∠A=900,四边形ABCD是平行四边形.∴∠C=∠A=900,
∠B=1800-∠A=900,
∠D=1800-∠A=900.求证:∠A=∠B=∠C=∠D=900.∴四边形ABCD是矩形.八年级 数学矩形的性质第十九章 四边形定理:矩形的两条对角线相等.已知:AC,BD是矩形ABCD的两条对角线.求证: AC=BD.证明:∵ 四边形ABCD是矩形,∴AB=DC,∠ABC=∠DCB=900.分析:根据矩形的性质性质,可转化为全等三角形(SAS)来证明.∵BC=CB,∴△ABC≌△DCB(SAS).∴AC=DB.八年级 数学矩形的性质第十九章 四边形设矩形的对角线AC与BD交于点E,那么,BE是Rt△ABC中一条怎样的特殊线段? 它与AC有什么大小关系?为什么?由此可得推论:
直角三角形斜边上的中线等于斜边的一半BE是Rt△ABC中斜边AC上的中线. BE等于AC的一半.∵ AC=BD,BE=DE,议一议:八年级 数学第十九章 四边形推论:直角三角形斜边上的中线等于斜边的一半.证明:延长CD到E使DE=CD,
连结AE、BE.∵AD = BD , DE =CD
∴四边形ACBE是平行四边形E?八年级 数学第十九章 四边形ODCBA相等的线段:相等的角:∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC ∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB等腰三角形有:△OAB △ OBC △OCD △OAD直角三角形有:Rt△ABC Rt△BCD Rt△CDA Rt△DAB全等三角形有:Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB
△OAB≌△OCD △OAD≌△OCB已知四边形ABCD是矩形思考:矩形ABCD是轴对称图形吗?它的对称轴有几条?矩形是中心对称图形吗?对称中心是?ABCDEFGH.八年级 数学第十九章 四边形矩形性质的应用 已知:如图,AC,BD是矩形ABCD的两条对线,AC,BD相交于点O,∠AOD=1200,AB=2.5cm.求矩形对角线的长.解:∵四边形ABCD是矩形,∴BD=2AB=2×2.5=5(cm).∴AC=BD,且∵∠DAB=900,∵∠AOD=1200,八年级 数学第十九章 四边形例2、例3教案.学案八年级 数学第十九章 四边形练一练:书本P104:练习3练习:如图四边形ABCD中,∠ABC=∠ADC=900,E是AC中点,EF平分∠BED交BD于点F,
(1)猜想EF与BD具有怎样的关系?
(2)试证明你的猜想。生活中的数学 给你一根足够长的绳子,你能检查教室的门窗或你的桌子是不是矩形吗?你怎样检查?解释其中的道理。八年级 数学学以致用第十九章 四边形四边形ABCD是矩形
若已知AB=8㎝,AD=6㎝,
则AC= ㎝ OB= ㎝
若已知∠CAB=40°,则∠OCB=
∠OBA= ∠AOB= ∠AOD=
若已知AC=10㎝,BC=6㎝,则矩形的周长= ㎝
矩形的面积= ㎝2
4 若已知 ∠DOC=120°,AD=6㎝,则AC= ㎝550°10100°40°12482880°练一练八年级 数学第十九章 四边形学习了本节课你有哪些收获?
