【轻松备课-人教版九上】24.1.4 圆周角 课件
文档属性
| 名称 | 【轻松备课-人教版九上】24.1.4 圆周角 课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-08 13:51:03 | ||
图片预览



文档简介
(共26张PPT)
24.1 圆的有关性质
第二十四章 圆
24.1.4 圆周角
导入新课
讲授新课
当堂练习
课堂小结
1.理解圆周角的概念,会叙述并证明圆周角定理.
2.理解圆周角与圆心角的关系并能运用圆周角定理及推
论解决简单的几何问题.(重点)
3.了解圆周角的分类,会推理验证“圆周角与圆心角的
关系”.(难点)
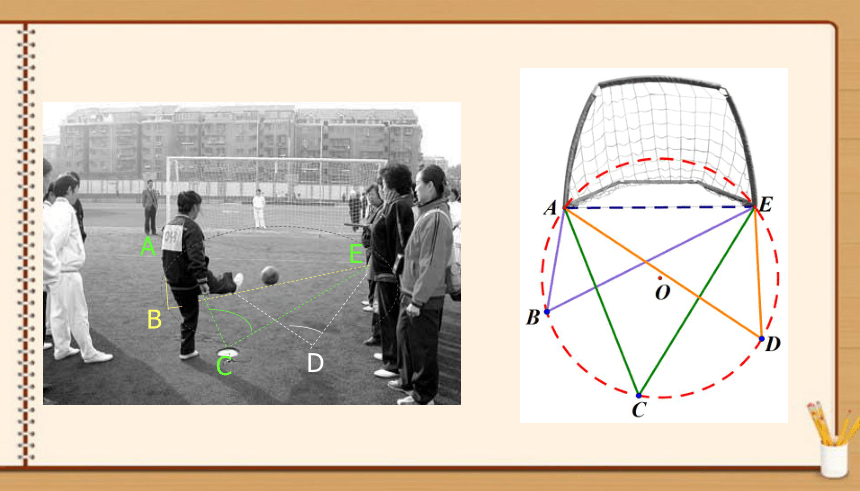
C
A
E
D
B
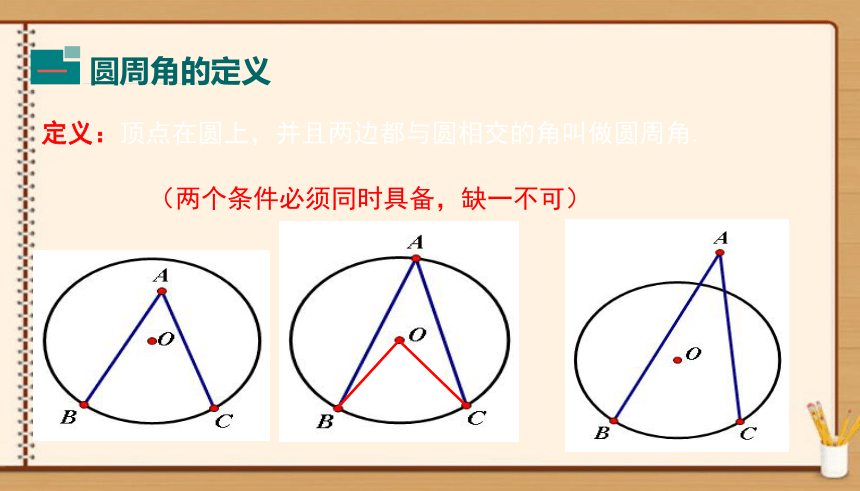
定义:顶点在圆上,并且两边都与圆相交的角叫做圆周角.
(两个条件必须同时具备,缺一不可)
圆周角的定义
一
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
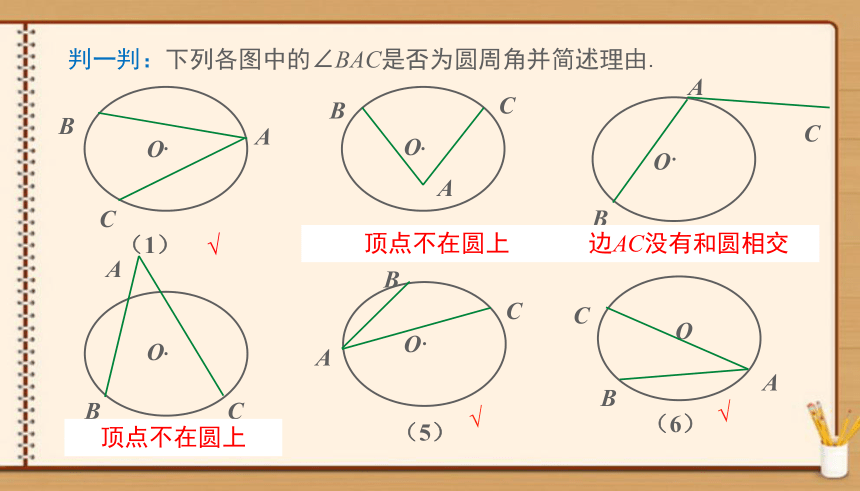
判一判:下列各图中的∠BAC是否为圆周角并简述理由.
(2)
(1)
(3)
(5)
(6)
顶点不在圆上
顶点不在圆上
边AC没有和圆相交
√
√
√
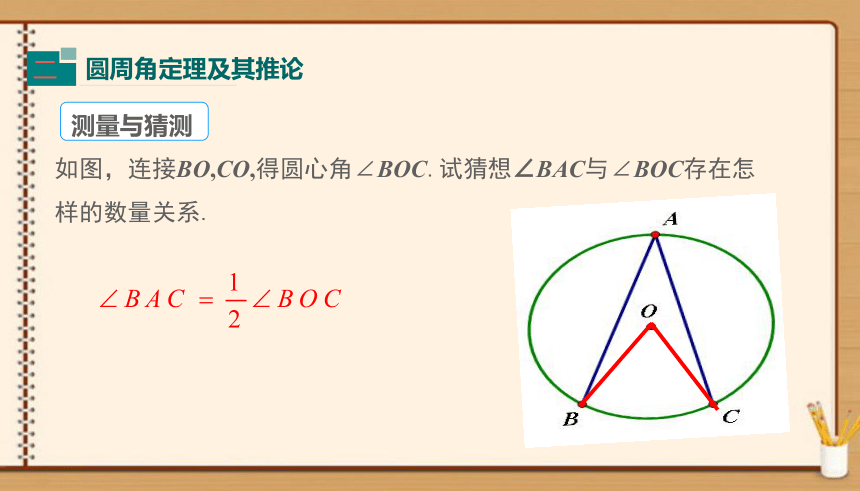
如图,连接BO,CO,得圆心角∠BOC.试猜想∠BAC与∠BOC存在怎样的数量关系.
圆周角定理及其推论
二
测量与猜测
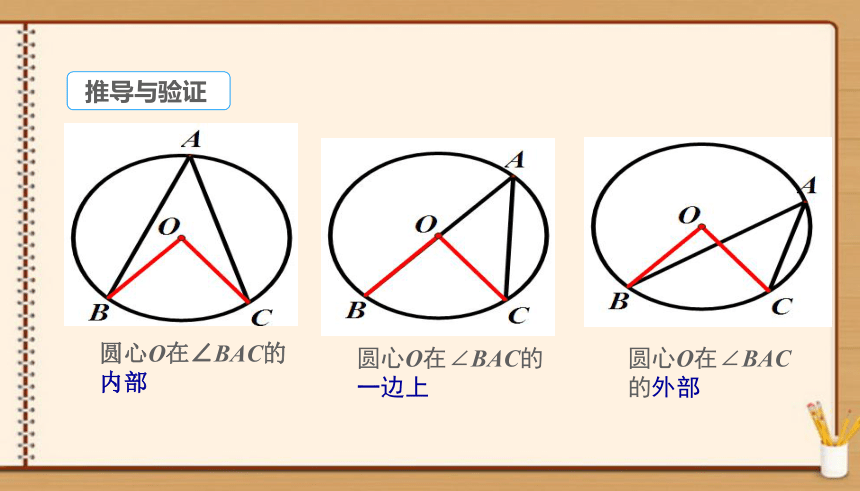
圆心O在∠BAC的 内部
圆心O在∠BAC的一边上
圆心O在∠BAC
的外部
推导与验证
圆心O在∠BAC的一边上(特殊情形)
OA=OC
∠A= ∠C
∠BOC= ∠ A+ ∠C
O
A
B
D
O
A
C
D
O
A
B
C
D
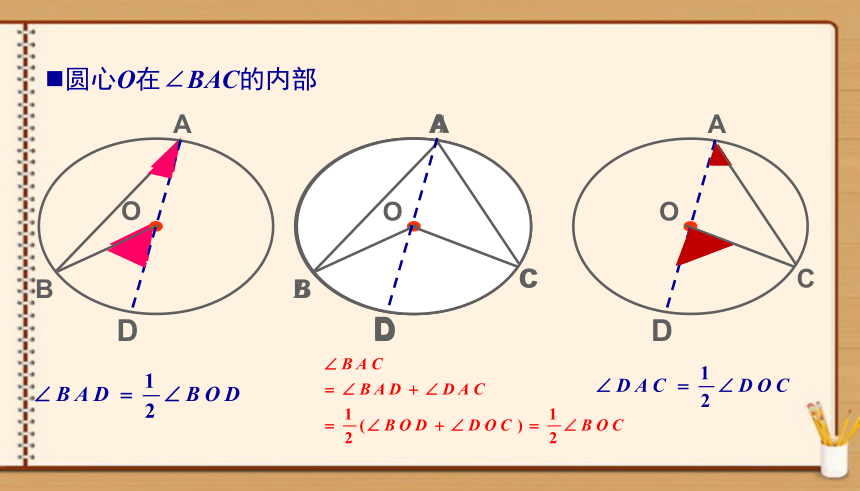
圆心O在∠BAC的内部
O
A
C
D
O
A
B
D
O
A
B
D
C
O
A
D
C
O
A
B
D
C
O
A
D
O
A
B
D
C
O
A
D
O
A
B
D
圆心O在∠BAC的外部
圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半.
要点归纳
圆周角定理及其推论
A1
A2
A3
推论1:
同弧所对的圆周角相等.
试一试:
1.如图,点A、B、C、D在☉O上,点A与点D在点B、C所在直线的同侧,∠BAC=35 .
(1)∠BOC= ,
理由是 ;
(2)∠BDC= ,理由是 .
70
35
同弧所对的圆周角相等
一条弧所对的圆周角等于该弧所对的圆心角的一半
(1)完成下列填空
∠1= .
∠2= .
∠3= .
∠5= .
2.如图,点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线.
∠4
∠8
∠6
∠7
A
B
C
D
O
1
(
(
(
(
(
(
(
(
2
3
4
5
6
7
8
2.如图,点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线.
(2)若AB=AD,则∠1与∠2是否相等,为什么?
⌒
⌒
推论2:等弧所对的圆周角相等
2.如图,点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线.
(3)若AC是半圆,
∠ADC= ,
∠ABC= .
90°
90°
若AC是直径,
推论3:半圆 所对的圆周角是直角.
(或直径)
反之,直角所对的弦是直径.
例:如图,⊙O直径AC为10cm,弦AD为6cm.
(1)求DC的长;
(2)若∠ADC的平分线交⊙O于B, 求AB、BC的长.
B
典例精析
解:(1)∵AC是直径,
∴ ∠ADC=90°.
在Rt△ADC中,
在Rt△ABC中,AB2+BC2=AC2,
(2)∵ AC是直径,
∴ ∠ABC=90°.
∵BD平分∠ADC,
∴∠ADB=∠CDB.
又∵∠ACB=∠ADB , ∠BAC=∠BDC .
∴ ∠BAC=∠ACB,
∴AB=BC.
B
解答圆周角有关问题时,若题中出现“直径”这个条件,则考虑构造直角三角形来求解.
归纳
若一个多边形各顶点都在同一个圆上,那么,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
圆内接四边形的定义
圆内接四边形
三
如图,四边形ABCD为⊙O的内接四边形,⊙O为四边形ABCD的外接圆.
探究性质
猜想:∠A与∠C, ∠B与∠D之间的关系为 .
∠A+ ∠C=180 ,∠B+ ∠D=180
圆内接四边形的性质:
圆内接四边形的对角互补.
练一练:
1.四边形ABCD是⊙O的内接四边形,且∠A=110°,∠B=80°,则∠C= ,∠D= .
2.⊙O的内接四边形ABCD中,∠A∶∠B∶∠C=1∶2∶3 ,则∠D= .
70
100
90
1.判断
(1)同一个圆中等弧所对的圆周角相等 ( )
(2)相等的弦所对的圆周角也相等 ( )
(3)900的角所对的弦是直径 ( )
(4)同弦所对的圆周角相等 ( )
√
×
×
×
2.如图,AB是⊙O的直径, C 、D是圆上的两点,∠ABD=40°,则∠BCD=____.
50°
3.已知△ABC的三个顶点在⊙O上,∠BAC=50°,∠ABC=47°
,则∠AOB= .
A
B
O
C
D
第2题
B
A
C
O
第3题
166°
4.如图,已知圆心角∠AOB=100°,则圆周角∠ACB= ,
∠ADB= .
D
A
O
C
B
130°
50°
5.如图,△ABC的顶点A、B、C
都在⊙O上,∠C=30 °,AB=2,
则⊙O的半径是 .
C
A
B
O
解:连接OA、OB
∵∠C=30 ° ,∴∠AOB=60 °
又∵OA=OB ,∴△AOB是等边三角形
∴OA=OB=AB=2,即半径为2。
2
6.如图,∠A=50°, ∠ABC=60 °,BD是⊙O的直径,则∠AEB等于 ( )
A.70° B.110° C.90° D.120°
B
A
C
B
O
D
E
拓展提升:如图,在△ABC中,AB=AC,以AB为直径的圆交BC于D,交AC于E.
(1)BD与CD的大小有什么关系 为什么
(2)求证: .
A
B
C
D
E
∵AB是圆的直径,点D在圆上,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=CD,
AD平分顶角∠BAC,即∠BAD=∠CAD,
(同圆或等圆中相等的圆周角所对弧相等).
解:BD=CD.理由是:连接AD,
圆心角
类比
圆周角
圆周角定义
圆周角定理
圆周角定理的推论
一条弧所对的圆周角等于它所对的圆心角的一半.
1.同弧(或等弧)所对的圆周角相等;2.半圆所对的圆周角是直角;反之,直角所对的弦是直径.
1.顶点在圆上,2.两边都与圆相交的角(二者必须同时具备)
24.1 圆的有关性质
第二十四章 圆
24.1.4 圆周角
导入新课
讲授新课
当堂练习
课堂小结
1.理解圆周角的概念,会叙述并证明圆周角定理.
2.理解圆周角与圆心角的关系并能运用圆周角定理及推
论解决简单的几何问题.(重点)
3.了解圆周角的分类,会推理验证“圆周角与圆心角的
关系”.(难点)
C
A
E
D
B
定义:顶点在圆上,并且两边都与圆相交的角叫做圆周角.
(两个条件必须同时具备,缺一不可)
圆周角的定义
一
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
判一判:下列各图中的∠BAC是否为圆周角并简述理由.
(2)
(1)
(3)
(5)
(6)
顶点不在圆上
顶点不在圆上
边AC没有和圆相交
√
√
√
如图,连接BO,CO,得圆心角∠BOC.试猜想∠BAC与∠BOC存在怎样的数量关系.
圆周角定理及其推论
二
测量与猜测
圆心O在∠BAC的 内部
圆心O在∠BAC的一边上
圆心O在∠BAC
的外部
推导与验证
圆心O在∠BAC的一边上(特殊情形)
OA=OC
∠A= ∠C
∠BOC= ∠ A+ ∠C
O
A
B
D
O
A
C
D
O
A
B
C
D
圆心O在∠BAC的内部
O
A
C
D
O
A
B
D
O
A
B
D
C
O
A
D
C
O
A
B
D
C
O
A
D
O
A
B
D
C
O
A
D
O
A
B
D
圆心O在∠BAC的外部
圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半.
要点归纳
圆周角定理及其推论
A1
A2
A3
推论1:
同弧所对的圆周角相等.
试一试:
1.如图,点A、B、C、D在☉O上,点A与点D在点B、C所在直线的同侧,∠BAC=35 .
(1)∠BOC= ,
理由是 ;
(2)∠BDC= ,理由是 .
70
35
同弧所对的圆周角相等
一条弧所对的圆周角等于该弧所对的圆心角的一半
(1)完成下列填空
∠1= .
∠2= .
∠3= .
∠5= .
2.如图,点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线.
∠4
∠8
∠6
∠7
A
B
C
D
O
1
(
(
(
(
(
(
(
(
2
3
4
5
6
7
8
2.如图,点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线.
(2)若AB=AD,则∠1与∠2是否相等,为什么?
⌒
⌒
推论2:等弧所对的圆周角相等
2.如图,点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线.
(3)若AC是半圆,
∠ADC= ,
∠ABC= .
90°
90°
若AC是直径,
推论3:半圆 所对的圆周角是直角.
(或直径)
反之,直角所对的弦是直径.
例:如图,⊙O直径AC为10cm,弦AD为6cm.
(1)求DC的长;
(2)若∠ADC的平分线交⊙O于B, 求AB、BC的长.
B
典例精析
解:(1)∵AC是直径,
∴ ∠ADC=90°.
在Rt△ADC中,
在Rt△ABC中,AB2+BC2=AC2,
(2)∵ AC是直径,
∴ ∠ABC=90°.
∵BD平分∠ADC,
∴∠ADB=∠CDB.
又∵∠ACB=∠ADB , ∠BAC=∠BDC .
∴ ∠BAC=∠ACB,
∴AB=BC.
B
解答圆周角有关问题时,若题中出现“直径”这个条件,则考虑构造直角三角形来求解.
归纳
若一个多边形各顶点都在同一个圆上,那么,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
圆内接四边形的定义
圆内接四边形
三
如图,四边形ABCD为⊙O的内接四边形,⊙O为四边形ABCD的外接圆.
探究性质
猜想:∠A与∠C, ∠B与∠D之间的关系为 .
∠A+ ∠C=180 ,∠B+ ∠D=180
圆内接四边形的性质:
圆内接四边形的对角互补.
练一练:
1.四边形ABCD是⊙O的内接四边形,且∠A=110°,∠B=80°,则∠C= ,∠D= .
2.⊙O的内接四边形ABCD中,∠A∶∠B∶∠C=1∶2∶3 ,则∠D= .
70
100
90
1.判断
(1)同一个圆中等弧所对的圆周角相等 ( )
(2)相等的弦所对的圆周角也相等 ( )
(3)900的角所对的弦是直径 ( )
(4)同弦所对的圆周角相等 ( )
√
×
×
×
2.如图,AB是⊙O的直径, C 、D是圆上的两点,∠ABD=40°,则∠BCD=____.
50°
3.已知△ABC的三个顶点在⊙O上,∠BAC=50°,∠ABC=47°
,则∠AOB= .
A
B
O
C
D
第2题
B
A
C
O
第3题
166°
4.如图,已知圆心角∠AOB=100°,则圆周角∠ACB= ,
∠ADB= .
D
A
O
C
B
130°
50°
5.如图,△ABC的顶点A、B、C
都在⊙O上,∠C=30 °,AB=2,
则⊙O的半径是 .
C
A
B
O
解:连接OA、OB
∵∠C=30 ° ,∴∠AOB=60 °
又∵OA=OB ,∴△AOB是等边三角形
∴OA=OB=AB=2,即半径为2。
2
6.如图,∠A=50°, ∠ABC=60 °,BD是⊙O的直径,则∠AEB等于 ( )
A.70° B.110° C.90° D.120°
B
A
C
B
O
D
E
拓展提升:如图,在△ABC中,AB=AC,以AB为直径的圆交BC于D,交AC于E.
(1)BD与CD的大小有什么关系 为什么
(2)求证: .
A
B
C
D
E
∵AB是圆的直径,点D在圆上,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=CD,
AD平分顶角∠BAC,即∠BAD=∠CAD,
(同圆或等圆中相等的圆周角所对弧相等).
解:BD=CD.理由是:连接AD,
圆心角
类比
圆周角
圆周角定义
圆周角定理
圆周角定理的推论
一条弧所对的圆周角等于它所对的圆心角的一半.
1.同弧(或等弧)所对的圆周角相等;2.半圆所对的圆周角是直角;反之,直角所对的弦是直径.
1.顶点在圆上,2.两边都与圆相交的角(二者必须同时具备)
同课章节目录
