11.1 平面内点的坐标 同步练习(含解析) 2022-2023学年上学期安徽省八年级数学期末试题选编
文档属性
| 名称 | 11.1 平面内点的坐标 同步练习(含解析) 2022-2023学年上学期安徽省八年级数学期末试题选编 |

|
|
| 格式 | docx | ||
| 文件大小 | 300.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-05 00:00:00 | ||
图片预览



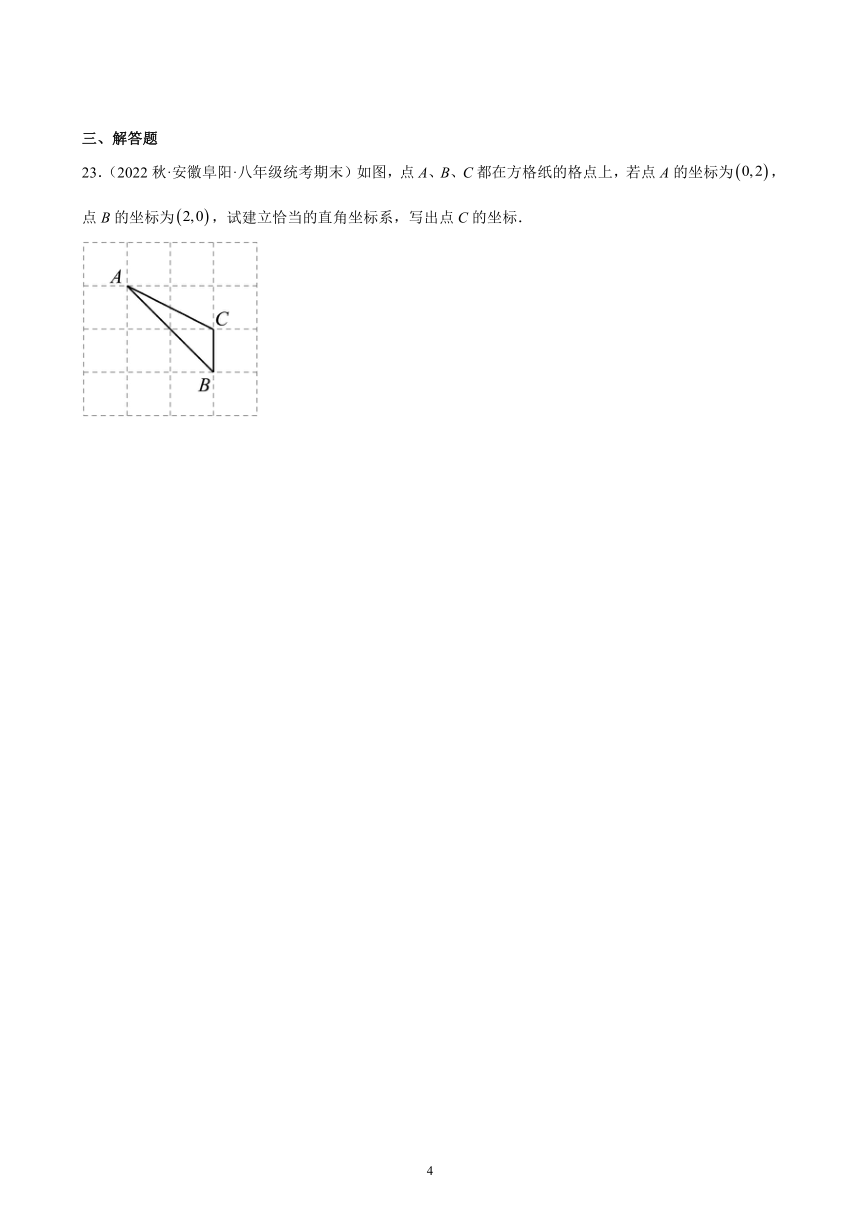

文档简介
11.1 平面内点的坐标
一、单选题
1.(2022秋·安徽合肥·八年级统考期末)已知点的坐标为,点的坐标为,平行于轴,则点的坐标为( )
A. B. C. D.
2.(2022秋·安徽滁州·八年级统考期末)在平面直角坐标系点P(-3,4)到x轴的距离是( )
A.4 B.3 C.5 D.-3
3.(2022秋·安徽合肥·八年级统考期末)点P在第二象限内,点P到x轴的距离是6,到y轴的距离是2,那么点P的坐标为( )
A.(﹣6,2) B.(﹣2,﹣6) C.(﹣2,6) D.(2,﹣6)
4.(2022秋·安徽蚌埠·八年级统考期末)点A(﹣3,4)离y轴的距离是( )
A.3 B.4 C.5 D.7
5.(2022秋·安徽亳州·八年级统考期末)在平面直角坐标系中,点P(5,-3)在( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.(2022秋·安徽淮北·八年级统考期末)如图,小手盖住的点的坐标可能为( )
A. B. C. D.
7.(2022秋·安徽宿州·八年级统考期末)在直角坐标系的x轴的负半轴上,则点P坐标为( )
A. B. C. D.
8.(2022秋·安徽安庆·八年级统考期末)已知点P位于第二象限,则点P的坐标可能是( )
A.(﹣2,0) B.(0,4) C.(﹣2,3) D.(2,﹣3)
9.(2022秋·安徽六安·八年级统考期末)点在第二象限内,其纵、横坐标均为整数,则( )
A.0 B.1 C.2 D.3
10.(2022秋·安徽·八年级统考期末)在平面直角坐标系中,若点在第二象限,则x是( )
A.正数 B.负数 C.正数或0 D.任意数
11.(2022秋·安徽安庆·八年级统考期末)在平面直角坐标系中,已知点A(m﹣1,2m﹣2),B(﹣3,2).若直线ABy轴,则线段AB的长为( )
A.2 B.4 C.6 D.8
12.(2022秋·安徽淮北·八年级统考期末)已知点,,则直线PQ( )
A.平行于x轴 B.平行于y轴 C.垂直于x轴 D.以上都不正确
13.(2022秋·安徽安庆·八年级统考期末)如图在正方形网格中,若A(1,1),B(2,0),则C点的坐标为( )
A.(-3,-2) B.(3,-2) C.(-2,-3) D.(2,-3)
14.(2022秋·安徽合肥·八年级统考期末)如图,动点在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点,第2次接着运动到点,第3次接着运动到点,…,按这样的运动规律,经过第2022次运动后,动点的坐标是( )
A. B. C. D.
15.(2022秋·安徽六安·八年级统考期末)在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m,其行走路线如图所示,第1次移动到,第2次移动到,…,第n次移动到,则的面积是( )
A. B. C. D.
16.(2022秋·安徽蚌埠·八年级统考期末)如图,围棋棋盘放在某平面直角坐标系内,已知棋子甲的坐标为,棋子乙的坐标为,则棋子丙的坐标是( )
A. B. C. D.
17.(2022秋·安徽宿州·八年级统考期末)2021年9月15日,中华人民共和国第十四届运动会开幕式在西安奥体中心举行,如图,如果将西安钟楼的位置记为直角坐标系的原点,下列哪个点的位置可以表示奥体中心的位置( )
A.(-2,3) B.(2,3) C.(-2,-3) D.(2,-3)
18.(2022秋·安徽宣城·八年级统考期末)以下能够准确表示宣城市政府地理位置的是( )
A.离上海市282千米 B.在上海市南偏西
C.在上海市南偏西282千米 D.东经,北纬
二、填空题
19.(2022秋·安徽池州·八年级统考期末)已知点A(a,b)在x轴上,则ab= .
20.(2022秋·安徽安庆·八年级统考期末)点在x轴上,则 .
21.(2022秋·安徽宣城·八年级统考期末)若点P位于第二象限,且距x轴的距离为2个单位长度,距y轴的距离为3个单位长度,则点P的坐标是 .
22.(2022秋·安徽淮北·八年级统考期末)已知点的坐标为,且点到两坐标轴的距离相等,则 .
三、解答题
23.(2022秋·安徽阜阳·八年级统考期末)如图,点A、B、C都在方格纸的格点上,若点A的坐标为,点B的坐标为,试建立恰当的直角坐标系,写出点C的坐标.
参考答案:
1.A
【分析】由平行于轴可得上任意点的横坐标都相等,从而,解得,代入即可.
【详解】解:点的坐标为,点的坐标为,平行于轴,
,解得,
,
故选:A.
【点睛】本题考查平行于轴直线上点的坐标特征,根据性质列出方程求解是解决问题的关键.
2.A
【分析】点到x轴的距离为纵坐标的绝对值,即可求解.
【详解】解:点到x轴的距离为,
故选:A.
【点睛】本题考查点到坐标轴的距离,点到横轴的距离为纵坐标的绝对值,到纵轴的距离为横坐标的绝对值.
3.C
【分析】根据点(x,y)到x轴的距离为|y|,到y轴的距离|x|解答即可.
【详解】解:设点P坐标为(x,y),
∵点P到x轴的距离是6,到y轴的距离是2,
∴|y|=6,|x|=2,
∵点P在第二象限内,
∴y=6,x=-2,
∴点P坐标为(-2,6),
故选:C.
【点睛】本题考查点到坐标轴的距离、点所在的象限,熟知点到坐标轴的距离与坐标的关系是解答的关键.
4.A
【分析】根据点在平面直角坐标系中的坐标的几何意义求解即可.
【详解】解:点A(﹣3,4)离y轴的距离是
故选A
【点睛】此题考查了点到坐标轴的距离,解题的关键是理解平面直角坐标系中点坐标的几何意义.
5.D
【分析】根据点的横纵坐标特点,判断其所在象限,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
【详解】解:∵点P(5,-3)的横纵坐标符号分别为: +,-,
∴点P(5,-3)位于第四象限.
故选:D.
【点睛】本题考查了各象限内点的坐标的符号,记住各象限内点的坐标的符号是解决的关键.
6.C
【分析】根据盖住的点是第三象限的点,然后根据各象限内点的坐标特征对各选项分析判断后利用排除法求解.
【详解】解:盖住的点是第三象限的点,
A.(2,2)在第一象限,故本选项错误;
B.(-2,2)在第二象限,故本选项错误;
C.(-2,-2)在第三象限,故本选项正确;
D.(2,-2)在第四象限,故本选项错误.
故选:C.
【点睛】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
7.A
【分析】根据x轴负半轴上的点的特征进行判断.
【详解】解:A、( 4,0)在x轴负半轴上,正确;
B、(0,4) 在y轴正半轴上,错误;
C、(0, 3) 在y轴负半轴上,错误;
D、(1,0) 在x轴正半轴上,错误;
故选择A.
【点睛】本题考查平行直角坐标系在坐标轴上点的坐标特征:x轴上的点纵坐标为0,y轴上的点横坐标为0.
8.C
【分析】根据第二象限的点横坐标为负,纵坐标为正进行判断即可.
【详解】解:A. (﹣2,0)在x轴上;
B. (0,4)在y轴上;
C. (﹣2,3)在第二象限;
D. (2,﹣3)在第四象限;
故选:C.
【点睛】本题考查了象限内点的坐标的特征,解题关键是明确不同象限内点的符号特征.
9.C
【分析】根据第二象限内点的横坐标小于零,纵坐标大于零,可得不等式组,根据解不等式组,可得答案.
【详解】解:∵点在第二象限内,
∴,解得:,
∵纵、横坐标均为整数,
∴,
故选C.
【点睛】本题考查了各象限内点的坐标的符号特征以及解不等式,记住各象限内点的坐标的符号是解决的关键.
10.A
【分析】根据第二象限,点的符号特征,进行判断即可.
【详解】解:∵第二象限,点的符号特征是,
∴,是正数;
故选A.
【点睛】本题考查坐标系下象限内点的符号特征.熟练掌握象限内点的符号特征,是解题的关键.
11.D
【分析】根据平行于轴的直线的横坐标相等,求得的值,进而求得点的坐标,即可求解.
【详解】解:∵直线ABy轴,A(m﹣1,2m﹣2),B(﹣3,2),
∴,
解得,
∴,
即,
∴,
故选D.
【点睛】本题考查了坐标与图形,求得的值是解题的关键.
12.A
【分析】根据平行于x轴的点的纵坐标相等解答.
【详解】解:∵,都在第二象限,纵坐标都是5,
∴轴,故A正确.
故选:A.
【点睛】本题考查了坐标与图形性质,主要利用了平行于x轴的直线上的点的坐标特征.
13.B
【分析】根据A(1,1),B(2,0),可得出原点的坐标,再结合图形即可确定出点C的坐标.
【详解】解:∵点A的坐标是:(1,1),点B的坐标是:(2,0),
∴原点坐标如下图所示:
∴点C的坐标是:(3,-2).
故选B.
【点睛】考查了点的坐标.点的坐标就是在平面直角坐标系中,坐标平面内的点与一对有序实数是一一对应的关系,这对有序实数则为这个点的坐标.
14.B
【分析】观察图形可知:每4次运动为一个循环,并且每一个循环向左运动4个单位,用2022÷4可判断出第2022次运动时,点P在第几个循环后的第几次运动中,进一步即可计算出坐标.
【详解】解:动点P的运动规律可以看作每运动四次为一个循环,每个循环向左运动4个单位,
∵2022÷4=505……2,
∴第2022次运动时,
点P在第506次循环后的第2次运动上,
∴横坐标为,纵坐标为0,
∴此时P(-2022,0).
故选:B.
【点睛】本题考查规律型:点坐标,解答时注意探究点的运动规律,又要注意动点的坐标的象限符号.
15.B
【分析】每四次一循环,每个循环,点向x轴的正方向前进2m,由于2019=504×4+3,则可判断点,然后根据三角形面积公式求出.
【详解】解:A1(1,0),A2(1,1),A3(2,1),A4(2,0),A5(3,0),A6(3,1),…,
每四次一循环,每个循环,点向x轴的正方向前进2m,
∴OA4n=2n,
∵2019=504×4+3,
∴点,且,
∴的面积=(m2).
故选:B.
【点睛】本题主要考查了点的坐标的变化规律,解题的关键是根据图形得出下标为4的倍数时对应长度即为下标的一半.
16.D
【分析】先利用棋子甲的坐标为(-2,2)画出直角坐标系,然后可写出棋子丙的坐标.
【详解】解:建立如图所示的平面直角坐标系:
棋子丙的坐标是.
故选:D.
【点睛】本题考查了坐标确定位置:平面内的点与有序实数对一一对应;记住平面内特殊位置的点的坐标特征.
17.B
【分析】熟记各象限内点的符号特征,第一象限(+,+),第二象限(-,+),第三象限(-,-),第四象限(+,-),直接利用已知平面直角坐标系得出奥体中心的位置.
【详解】解:由题意可得:奥体中心的位置可以为(2,3).
故选:B.
【点睛】此题主要考查了坐标确定位置,正确理解平面直角坐标系的意义是解题关键.
18.D
【分析】根据点的坐标的定义,确定一个位置需要两个数据解答即可.
【详解】解:能够准确表示宣城市政府地理位置的是:东经30.8°,北纬118°.
故选:D.
【点睛】本题考查了坐标确定位置,是基础题,理解坐标的定义是解题的关键.
19.0
【分析】直接利用x轴上点的坐标特点,得出答案.
【详解】∵点A(a,b)在x轴上,
∴b=0.
∴ab=0.
故答案为:0.
【点睛】本题主要考查x轴上点的坐标特点,掌握x轴上点的纵坐标为0,是解题的关键.
20.
【分析】根据x轴上点的纵坐标为0即可求出答案.
【详解】解:点在x轴上,
,
,
故答案为:.
【点睛】本题考查坐标轴上点的特征,要熟记x轴上点的纵坐标为0,y轴上点的横坐标为0.
21.
【分析】利用第二象限内点的坐标特征和点的坐标的表示方法求解.
【详解】解:∵点P位于第二象限,且距x轴的距离为2个单位长度,距y轴的距离为3个单位长度,
∴点P的坐标为(-3,2)
故答案为:(-3,2)
【点睛】本题考查了点的坐标:平面直角坐标系内的点与有序实数对是一一对应的关系,记住各象限点的坐标特征,理解坐标的意义是解题的关键.
22.4或1
【分析】分点的横坐标与纵坐标相等和互为相反数两种情况讨论求解.
【详解】解:∵点P(a+2,3a-6)到两坐标轴的距离相等,
∴a+2=3a-6或a+2+3a-6=0,
解得a=4或a=1,
故答案为:4或1.
【点睛】本题考查了点的坐标,难点在于分情况讨论.
23.图见解析,
【分析】根据点的坐标建立坐标系,再确定坐标.
【详解】解:如图所示建立直角坐标系:
∴点C的坐标为(2,1).
【点睛】本题考查了坐标系及其点的坐标,正确建立平面直角坐标系是解题的关键.
一、单选题
1.(2022秋·安徽合肥·八年级统考期末)已知点的坐标为,点的坐标为,平行于轴,则点的坐标为( )
A. B. C. D.
2.(2022秋·安徽滁州·八年级统考期末)在平面直角坐标系点P(-3,4)到x轴的距离是( )
A.4 B.3 C.5 D.-3
3.(2022秋·安徽合肥·八年级统考期末)点P在第二象限内,点P到x轴的距离是6,到y轴的距离是2,那么点P的坐标为( )
A.(﹣6,2) B.(﹣2,﹣6) C.(﹣2,6) D.(2,﹣6)
4.(2022秋·安徽蚌埠·八年级统考期末)点A(﹣3,4)离y轴的距离是( )
A.3 B.4 C.5 D.7
5.(2022秋·安徽亳州·八年级统考期末)在平面直角坐标系中,点P(5,-3)在( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.(2022秋·安徽淮北·八年级统考期末)如图,小手盖住的点的坐标可能为( )
A. B. C. D.
7.(2022秋·安徽宿州·八年级统考期末)在直角坐标系的x轴的负半轴上,则点P坐标为( )
A. B. C. D.
8.(2022秋·安徽安庆·八年级统考期末)已知点P位于第二象限,则点P的坐标可能是( )
A.(﹣2,0) B.(0,4) C.(﹣2,3) D.(2,﹣3)
9.(2022秋·安徽六安·八年级统考期末)点在第二象限内,其纵、横坐标均为整数,则( )
A.0 B.1 C.2 D.3
10.(2022秋·安徽·八年级统考期末)在平面直角坐标系中,若点在第二象限,则x是( )
A.正数 B.负数 C.正数或0 D.任意数
11.(2022秋·安徽安庆·八年级统考期末)在平面直角坐标系中,已知点A(m﹣1,2m﹣2),B(﹣3,2).若直线ABy轴,则线段AB的长为( )
A.2 B.4 C.6 D.8
12.(2022秋·安徽淮北·八年级统考期末)已知点,,则直线PQ( )
A.平行于x轴 B.平行于y轴 C.垂直于x轴 D.以上都不正确
13.(2022秋·安徽安庆·八年级统考期末)如图在正方形网格中,若A(1,1),B(2,0),则C点的坐标为( )
A.(-3,-2) B.(3,-2) C.(-2,-3) D.(2,-3)
14.(2022秋·安徽合肥·八年级统考期末)如图,动点在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点,第2次接着运动到点,第3次接着运动到点,…,按这样的运动规律,经过第2022次运动后,动点的坐标是( )
A. B. C. D.
15.(2022秋·安徽六安·八年级统考期末)在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m,其行走路线如图所示,第1次移动到,第2次移动到,…,第n次移动到,则的面积是( )
A. B. C. D.
16.(2022秋·安徽蚌埠·八年级统考期末)如图,围棋棋盘放在某平面直角坐标系内,已知棋子甲的坐标为,棋子乙的坐标为,则棋子丙的坐标是( )
A. B. C. D.
17.(2022秋·安徽宿州·八年级统考期末)2021年9月15日,中华人民共和国第十四届运动会开幕式在西安奥体中心举行,如图,如果将西安钟楼的位置记为直角坐标系的原点,下列哪个点的位置可以表示奥体中心的位置( )
A.(-2,3) B.(2,3) C.(-2,-3) D.(2,-3)
18.(2022秋·安徽宣城·八年级统考期末)以下能够准确表示宣城市政府地理位置的是( )
A.离上海市282千米 B.在上海市南偏西
C.在上海市南偏西282千米 D.东经,北纬
二、填空题
19.(2022秋·安徽池州·八年级统考期末)已知点A(a,b)在x轴上,则ab= .
20.(2022秋·安徽安庆·八年级统考期末)点在x轴上,则 .
21.(2022秋·安徽宣城·八年级统考期末)若点P位于第二象限,且距x轴的距离为2个单位长度,距y轴的距离为3个单位长度,则点P的坐标是 .
22.(2022秋·安徽淮北·八年级统考期末)已知点的坐标为,且点到两坐标轴的距离相等,则 .
三、解答题
23.(2022秋·安徽阜阳·八年级统考期末)如图,点A、B、C都在方格纸的格点上,若点A的坐标为,点B的坐标为,试建立恰当的直角坐标系,写出点C的坐标.
参考答案:
1.A
【分析】由平行于轴可得上任意点的横坐标都相等,从而,解得,代入即可.
【详解】解:点的坐标为,点的坐标为,平行于轴,
,解得,
,
故选:A.
【点睛】本题考查平行于轴直线上点的坐标特征,根据性质列出方程求解是解决问题的关键.
2.A
【分析】点到x轴的距离为纵坐标的绝对值,即可求解.
【详解】解:点到x轴的距离为,
故选:A.
【点睛】本题考查点到坐标轴的距离,点到横轴的距离为纵坐标的绝对值,到纵轴的距离为横坐标的绝对值.
3.C
【分析】根据点(x,y)到x轴的距离为|y|,到y轴的距离|x|解答即可.
【详解】解:设点P坐标为(x,y),
∵点P到x轴的距离是6,到y轴的距离是2,
∴|y|=6,|x|=2,
∵点P在第二象限内,
∴y=6,x=-2,
∴点P坐标为(-2,6),
故选:C.
【点睛】本题考查点到坐标轴的距离、点所在的象限,熟知点到坐标轴的距离与坐标的关系是解答的关键.
4.A
【分析】根据点在平面直角坐标系中的坐标的几何意义求解即可.
【详解】解:点A(﹣3,4)离y轴的距离是
故选A
【点睛】此题考查了点到坐标轴的距离,解题的关键是理解平面直角坐标系中点坐标的几何意义.
5.D
【分析】根据点的横纵坐标特点,判断其所在象限,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
【详解】解:∵点P(5,-3)的横纵坐标符号分别为: +,-,
∴点P(5,-3)位于第四象限.
故选:D.
【点睛】本题考查了各象限内点的坐标的符号,记住各象限内点的坐标的符号是解决的关键.
6.C
【分析】根据盖住的点是第三象限的点,然后根据各象限内点的坐标特征对各选项分析判断后利用排除法求解.
【详解】解:盖住的点是第三象限的点,
A.(2,2)在第一象限,故本选项错误;
B.(-2,2)在第二象限,故本选项错误;
C.(-2,-2)在第三象限,故本选项正确;
D.(2,-2)在第四象限,故本选项错误.
故选:C.
【点睛】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
7.A
【分析】根据x轴负半轴上的点的特征进行判断.
【详解】解:A、( 4,0)在x轴负半轴上,正确;
B、(0,4) 在y轴正半轴上,错误;
C、(0, 3) 在y轴负半轴上,错误;
D、(1,0) 在x轴正半轴上,错误;
故选择A.
【点睛】本题考查平行直角坐标系在坐标轴上点的坐标特征:x轴上的点纵坐标为0,y轴上的点横坐标为0.
8.C
【分析】根据第二象限的点横坐标为负,纵坐标为正进行判断即可.
【详解】解:A. (﹣2,0)在x轴上;
B. (0,4)在y轴上;
C. (﹣2,3)在第二象限;
D. (2,﹣3)在第四象限;
故选:C.
【点睛】本题考查了象限内点的坐标的特征,解题关键是明确不同象限内点的符号特征.
9.C
【分析】根据第二象限内点的横坐标小于零,纵坐标大于零,可得不等式组,根据解不等式组,可得答案.
【详解】解:∵点在第二象限内,
∴,解得:,
∵纵、横坐标均为整数,
∴,
故选C.
【点睛】本题考查了各象限内点的坐标的符号特征以及解不等式,记住各象限内点的坐标的符号是解决的关键.
10.A
【分析】根据第二象限,点的符号特征,进行判断即可.
【详解】解:∵第二象限,点的符号特征是,
∴,是正数;
故选A.
【点睛】本题考查坐标系下象限内点的符号特征.熟练掌握象限内点的符号特征,是解题的关键.
11.D
【分析】根据平行于轴的直线的横坐标相等,求得的值,进而求得点的坐标,即可求解.
【详解】解:∵直线ABy轴,A(m﹣1,2m﹣2),B(﹣3,2),
∴,
解得,
∴,
即,
∴,
故选D.
【点睛】本题考查了坐标与图形,求得的值是解题的关键.
12.A
【分析】根据平行于x轴的点的纵坐标相等解答.
【详解】解:∵,都在第二象限,纵坐标都是5,
∴轴,故A正确.
故选:A.
【点睛】本题考查了坐标与图形性质,主要利用了平行于x轴的直线上的点的坐标特征.
13.B
【分析】根据A(1,1),B(2,0),可得出原点的坐标,再结合图形即可确定出点C的坐标.
【详解】解:∵点A的坐标是:(1,1),点B的坐标是:(2,0),
∴原点坐标如下图所示:
∴点C的坐标是:(3,-2).
故选B.
【点睛】考查了点的坐标.点的坐标就是在平面直角坐标系中,坐标平面内的点与一对有序实数是一一对应的关系,这对有序实数则为这个点的坐标.
14.B
【分析】观察图形可知:每4次运动为一个循环,并且每一个循环向左运动4个单位,用2022÷4可判断出第2022次运动时,点P在第几个循环后的第几次运动中,进一步即可计算出坐标.
【详解】解:动点P的运动规律可以看作每运动四次为一个循环,每个循环向左运动4个单位,
∵2022÷4=505……2,
∴第2022次运动时,
点P在第506次循环后的第2次运动上,
∴横坐标为,纵坐标为0,
∴此时P(-2022,0).
故选:B.
【点睛】本题考查规律型:点坐标,解答时注意探究点的运动规律,又要注意动点的坐标的象限符号.
15.B
【分析】每四次一循环,每个循环,点向x轴的正方向前进2m,由于2019=504×4+3,则可判断点,然后根据三角形面积公式求出.
【详解】解:A1(1,0),A2(1,1),A3(2,1),A4(2,0),A5(3,0),A6(3,1),…,
每四次一循环,每个循环,点向x轴的正方向前进2m,
∴OA4n=2n,
∵2019=504×4+3,
∴点,且,
∴的面积=(m2).
故选:B.
【点睛】本题主要考查了点的坐标的变化规律,解题的关键是根据图形得出下标为4的倍数时对应长度即为下标的一半.
16.D
【分析】先利用棋子甲的坐标为(-2,2)画出直角坐标系,然后可写出棋子丙的坐标.
【详解】解:建立如图所示的平面直角坐标系:
棋子丙的坐标是.
故选:D.
【点睛】本题考查了坐标确定位置:平面内的点与有序实数对一一对应;记住平面内特殊位置的点的坐标特征.
17.B
【分析】熟记各象限内点的符号特征,第一象限(+,+),第二象限(-,+),第三象限(-,-),第四象限(+,-),直接利用已知平面直角坐标系得出奥体中心的位置.
【详解】解:由题意可得:奥体中心的位置可以为(2,3).
故选:B.
【点睛】此题主要考查了坐标确定位置,正确理解平面直角坐标系的意义是解题关键.
18.D
【分析】根据点的坐标的定义,确定一个位置需要两个数据解答即可.
【详解】解:能够准确表示宣城市政府地理位置的是:东经30.8°,北纬118°.
故选:D.
【点睛】本题考查了坐标确定位置,是基础题,理解坐标的定义是解题的关键.
19.0
【分析】直接利用x轴上点的坐标特点,得出答案.
【详解】∵点A(a,b)在x轴上,
∴b=0.
∴ab=0.
故答案为:0.
【点睛】本题主要考查x轴上点的坐标特点,掌握x轴上点的纵坐标为0,是解题的关键.
20.
【分析】根据x轴上点的纵坐标为0即可求出答案.
【详解】解:点在x轴上,
,
,
故答案为:.
【点睛】本题考查坐标轴上点的特征,要熟记x轴上点的纵坐标为0,y轴上点的横坐标为0.
21.
【分析】利用第二象限内点的坐标特征和点的坐标的表示方法求解.
【详解】解:∵点P位于第二象限,且距x轴的距离为2个单位长度,距y轴的距离为3个单位长度,
∴点P的坐标为(-3,2)
故答案为:(-3,2)
【点睛】本题考查了点的坐标:平面直角坐标系内的点与有序实数对是一一对应的关系,记住各象限点的坐标特征,理解坐标的意义是解题的关键.
22.4或1
【分析】分点的横坐标与纵坐标相等和互为相反数两种情况讨论求解.
【详解】解:∵点P(a+2,3a-6)到两坐标轴的距离相等,
∴a+2=3a-6或a+2+3a-6=0,
解得a=4或a=1,
故答案为:4或1.
【点睛】本题考查了点的坐标,难点在于分情况讨论.
23.图见解析,
【分析】根据点的坐标建立坐标系,再确定坐标.
【详解】解:如图所示建立直角坐标系:
∴点C的坐标为(2,1).
【点睛】本题考查了坐标系及其点的坐标,正确建立平面直角坐标系是解题的关键.
