19.2.1 矩形(1)[下学期]
文档属性
| 名称 | 19.2.1 矩形(1)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 875.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-05-13 00:00:00 | ||
图片预览




文档简介
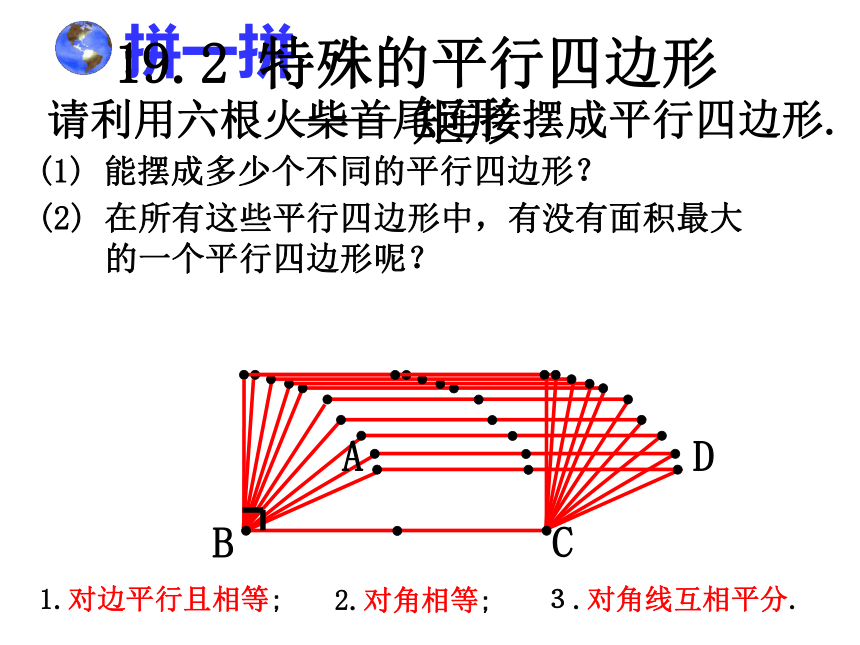
课件33张PPT。 §19.2.1 矩形 人教版八年级下册第十九章拼一拼 请利用六根火柴首尾连接摆成平行四边形. (1) 能摆成多少个不同的平行四边形? (2) 在所有这些平行四边形中,有没有面积最大
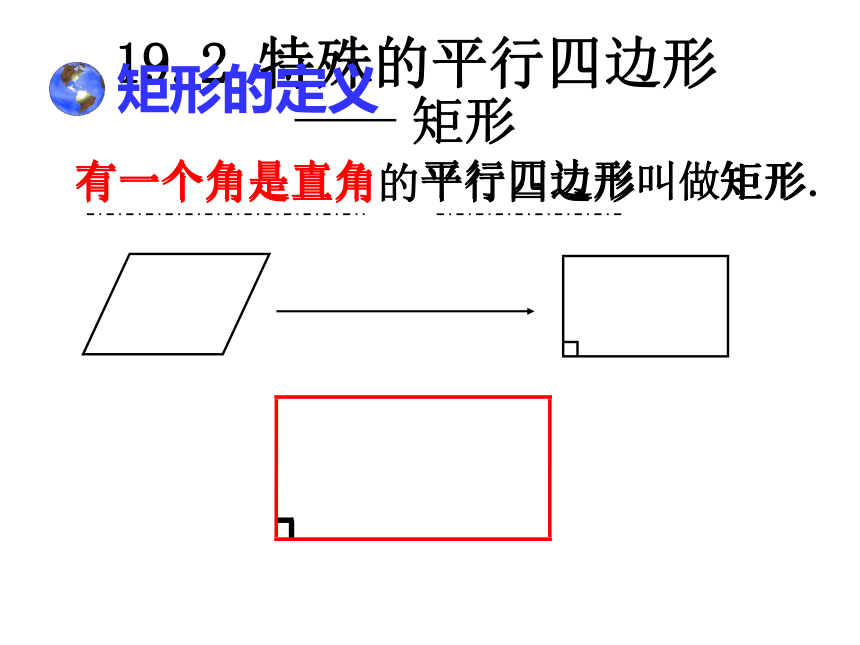
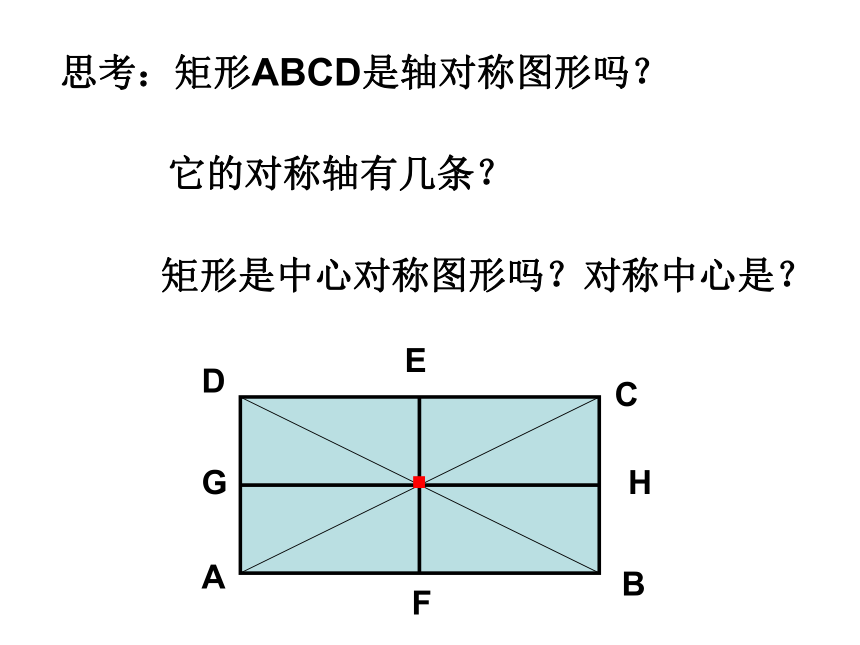
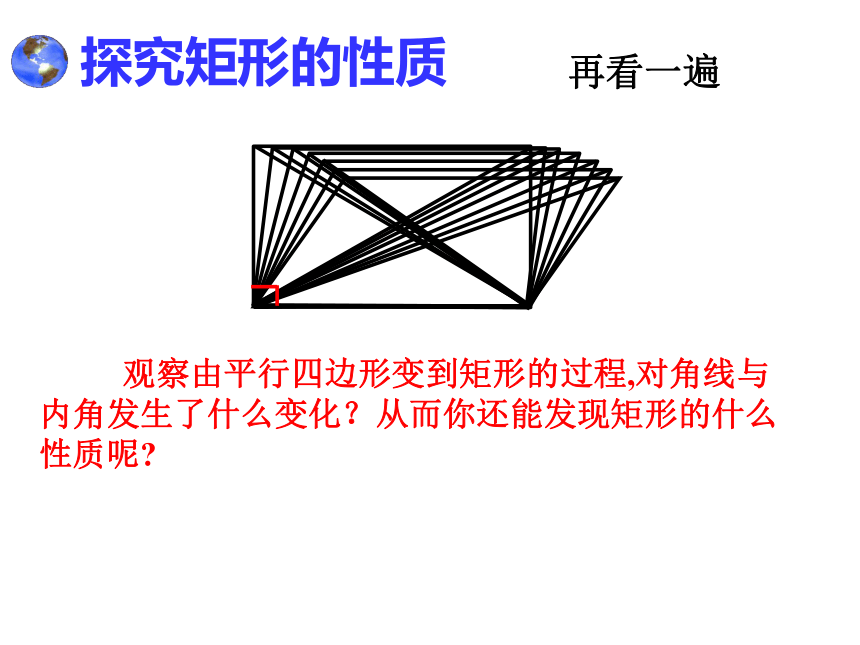
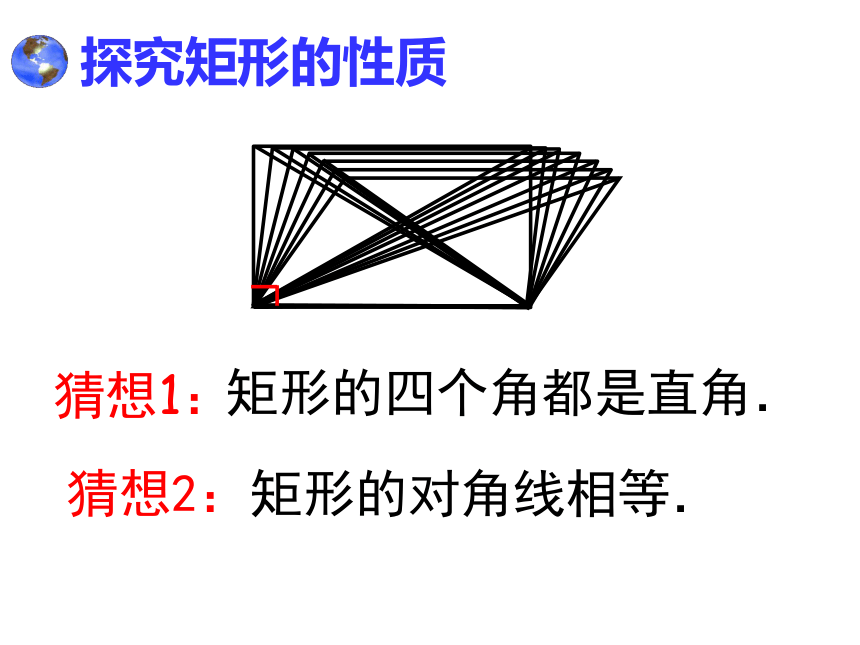
的一个平行四边形呢?19.2 特殊的平行四边形1.对边平行且相等;2.对角相等;3.对角线互相平分.平行四边形19.2 特殊的平行四边形 有一个角是直角的平行四边形矩形的定义叫做矩形.有一个角是直角矩形 思考:矩形ABCD是轴对称图形吗?它的对称轴有几条?矩形是中心对称图形吗?对称中心是?ABCDEFGH.探究矩形的性质再看一遍 观察由平行四边形变到矩形的过程,对角线与内角发生了什么变化?从而你还能发现矩形的什么性质呢?探究矩形的性质 矩形的四个角都是直角.猜想1:猜想2:矩形的对角线相等.矩形的四个角都是直角.已知:如图,四边形ABCD是矩形.分析:由矩形的定义,利用对角相等,邻角互补可使问题得证.证明:∵ 四边形ABCD是矩形,∴∠A=900,四边形ABCD是平行四边形.∴∠C=∠A=900,
∠B=1800-∠A=900,
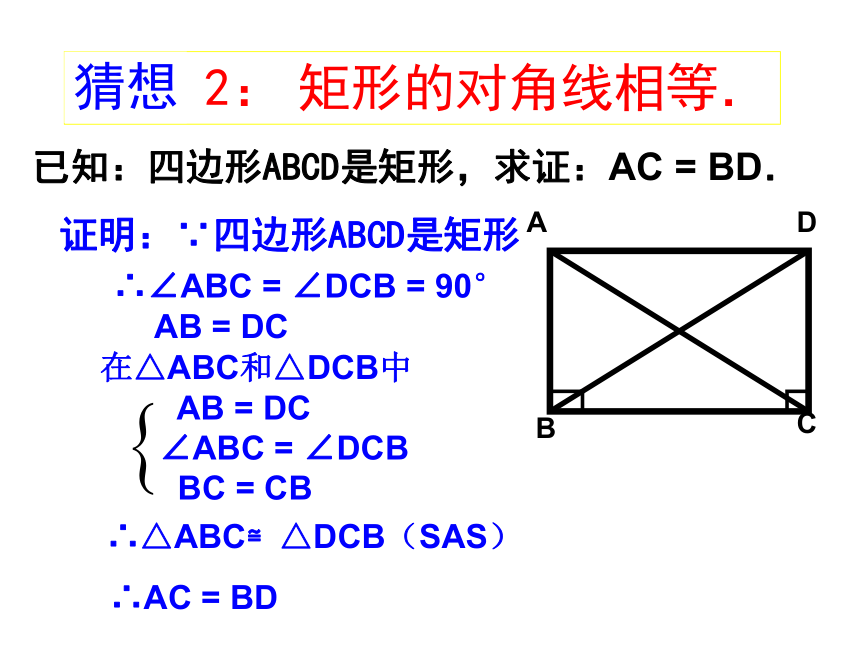
∠D=1800-∠A=900.求证:∠A=∠B=∠C=∠D=900.∴四边形ABCD是矩形.矩形的性质定理猜想已知:四边形ABCD是矩形,求证:AC = BD.证明:∵四边形ABCD是矩形∴∠ABC = ∠DCB = 90°∴△ABC≌△DCB(SAS) ∴AC = BD 2: 矩形的对角线相等.性质猜想在△ABC和△DCB中AB = DC AB = DC
∠ABC = ∠DCB
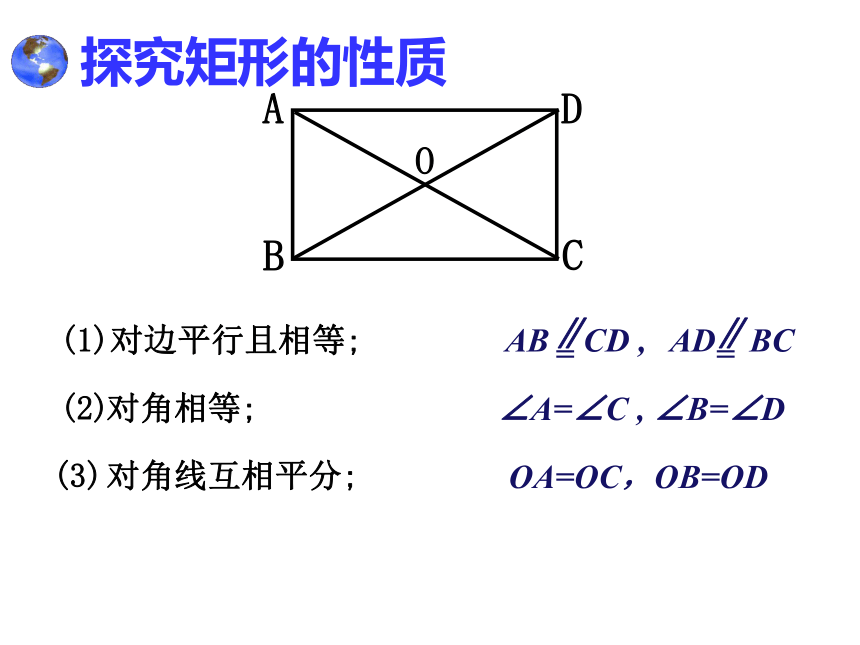
BC = CB探究矩形的性质O(1)对边平行且相等;(2) (3)∠A=∠C , ∠B=∠DOA=OC,OB=OD对角相等;对角线互相平分;OA=OC,OB=ODOA=OC=OB=OD∠BAD=∠BCD =∠ABC=∠ADC= 90°矩形的性质探究矩形的性质O(1)对边平行且相等;(2) (3)∠A=∠C , ∠B=∠D矩形的四个角都是直角;矩形的对角线相等对角相等;对角线互相平分;且互相平分;试一试1.矩形具有而一般平行四边形不具有的性
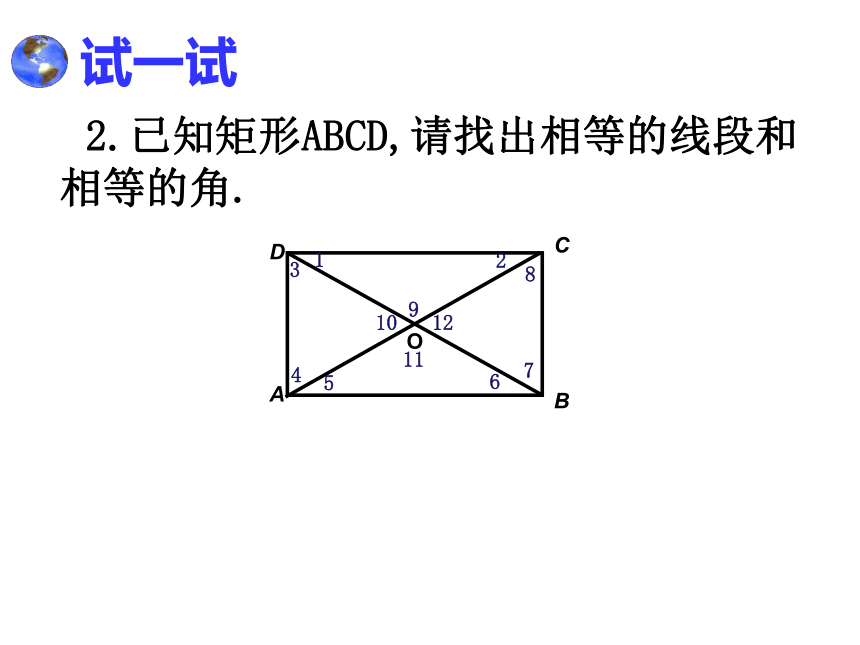
质是……………………………( ) C试一试2.已知矩形ABCD,请找出相等的线段和相等的角. 试一试3.已知矩形ABCD,请找出所有的直角三角形和等腰三角形. 矩形的问题可以转化到直角三角形或等腰三角形来解决. Rt△ADC、 Rt△DCB、
Rt△DAB、 Rt△ABC、△ADO、 △DOC、
△COB、 △AOB、共同练习 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4cm,求矩形对角线的长. 矩形的问题可以转化到直角三角形或等腰(边)三角形的问题来解决. 变式:若BD=8cm,∠AOD=120°,求 边AB的长。OABCD公平,因为OB=OD = OA=OC投圈游戏OABCDOB=OD = OA=OC推论:直角三角形斜边上的中线等于
斜边的一半。
= AC= BD 在 中,∠ABC=900 ,BO是斜边AC上的中线
OB = AC推论:直角三角形斜边上的中线等于斜边的一半.已知△ABC中∠ACB=90°,AD = BD
求证:CD = AB证明:延长CD到E使DE=CD,
连结AE、BE.∵AD = BD , DE =CD
∴四边形ACBE是平行四边形E?练一练 已知△ABC是Rt△,∠ABC=900,BD是斜边AC上的中线.(1)若 BD=3㎝,则AC=______ ㎝;
(2)若 ∠C=30°,AB=5㎝,则AC=_____㎝,
BD=_____㎝.6510 学海 无涯3.在 中,斜边AC上的中线
和高分别是6cm和5cm,则 的
面积S=( )。 A
BCDE30cm21.如图1,在矩形ABCD中,E、F是AB上的两点,且AE=BF,则
∠ ADE与 巩固 练习DA E F BC图1∠ BCF相等吗?为什么?2.如图2,矩形ABCD的对角线AC和BD相交于点O,CE//BD,交AB的延长线于点E,求证:AC=EC.A DBECO图23.已知:如图,在四边形ABCD中,∠ABC=∠ADC=900,M是AC的中点,N是
反馈 练习(1)试判断MD与MB的大小关系。
(2)试判断MN与BD的位置关系。
BD的中点。用一用 某学校因地制宜:先向北量6m,再向东量8m,接着向南量6m,最后向西量8m,在圈出的这块空地上建一个草坪.(1)圈出的空地是什么形状?(2)考虑到护理草坪,学校购置了一台自动喷水器, 这台机器的最大喷水距离为5m,问这台机器能对整个草坪进行护理吗?若能,则喷水器应安放在何处;若不能,请说明理由.O矩形的四个角均为直角矩形的对角线互相平分且相等矩形的对边平行且相等6868课堂小结1.知识小结2.学法小结(1)用类比的方法探究矩形的性质,先找共性再找特殊性,
并注意性质的整合;(2)矩形的问题常可以转化为直角三角形或等腰三角形
的问题来解决. 矩形ABCD中,AB= 4,BC=2,E是边CD 上的一点,AE=AB.求∠BEC的度数.课后作业课后练习:
如图,BD、CE是△ABC的高,G 、 F
分别是BC、DE的中点,求证:FG DE.AEBGCDF例2:如图,△ABC中,∠ACB=900,点D、E分别为AC、AB的中点,点F在BC延长线上,且∠CDF=∠A,
求证:四边形DECF是平行四边形;四边形ABCD是矩形
若已知AB=8㎝,AD=6㎝,
则AC= ㎝ OB= ㎝
若已知∠CAB=40°,则∠OCB=
∠OBA= ∠AOB= ∠AOD=
若已知AC=10㎝,BC=6㎝,则矩形的周长= ㎝
矩形的面积= ㎝2
4 若已知 ∠DOC=120°,AD=6㎝,则AC= ㎝550°10100°40°12482880°试一试如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线的长是13cm,那么矩形的周长是多少?
练一练:书本P104:练习3练习:如图四边形ABCD中,∠ABC=∠ADC=900,E是AC中点,EF平分∠BED交BD于点F,
(1)猜想EF与BD具有怎样的关系?
(2)试证明你的猜想。
再见投圈游戏 三位学生正在做投圈游戏,他们分别站在一个直角三角形的三个顶点处,目标物放在斜边的中点处,这样的队形对每个人公平吗? 在直角三角形中斜边上的中线等于斜边的一半. (1)随着∠a的变化,两条对角线的长度怎
样变化的?(2)当∠a变为直角时,平行四边形成为一个矩形,这时它的其他内角是什么样的角?(3)当∠a是直角时,平行四边形变成矩形,此时
两条对角线的长度有什么关系?随着∠a的变化,一条对角线在变长,
一条在变短。都变为了直角两条对角线相等活动一设矩形的对角线AC与BD交于点E,那么,BE是Rt△ABC中一条怎样的特殊线段? 它与AC有什么大小关系?为什么?由此可得推论:
直角三角形斜边上的中线等于斜边的一半BE是Rt△ABC中斜边AC上的中线. BE等于AC的一半.∵ AC=BD,BE=DE,议一议:八年级 数学第十九章 四边形
的一个平行四边形呢?19.2 特殊的平行四边形1.对边平行且相等;2.对角相等;3.对角线互相平分.平行四边形19.2 特殊的平行四边形 有一个角是直角的平行四边形矩形的定义叫做矩形.有一个角是直角矩形 思考:矩形ABCD是轴对称图形吗?它的对称轴有几条?矩形是中心对称图形吗?对称中心是?ABCDEFGH.探究矩形的性质再看一遍 观察由平行四边形变到矩形的过程,对角线与内角发生了什么变化?从而你还能发现矩形的什么性质呢?探究矩形的性质 矩形的四个角都是直角.猜想1:猜想2:矩形的对角线相等.矩形的四个角都是直角.已知:如图,四边形ABCD是矩形.分析:由矩形的定义,利用对角相等,邻角互补可使问题得证.证明:∵ 四边形ABCD是矩形,∴∠A=900,四边形ABCD是平行四边形.∴∠C=∠A=900,
∠B=1800-∠A=900,
∠D=1800-∠A=900.求证:∠A=∠B=∠C=∠D=900.∴四边形ABCD是矩形.矩形的性质定理猜想已知:四边形ABCD是矩形,求证:AC = BD.证明:∵四边形ABCD是矩形∴∠ABC = ∠DCB = 90°∴△ABC≌△DCB(SAS) ∴AC = BD 2: 矩形的对角线相等.性质猜想在△ABC和△DCB中AB = DC AB = DC
∠ABC = ∠DCB
BC = CB探究矩形的性质O(1)对边平行且相等;(2) (3)∠A=∠C , ∠B=∠DOA=OC,OB=OD对角相等;对角线互相平分;OA=OC,OB=ODOA=OC=OB=OD∠BAD=∠BCD =∠ABC=∠ADC= 90°矩形的性质探究矩形的性质O(1)对边平行且相等;(2) (3)∠A=∠C , ∠B=∠D矩形的四个角都是直角;矩形的对角线相等对角相等;对角线互相平分;且互相平分;试一试1.矩形具有而一般平行四边形不具有的性
质是……………………………( ) C试一试2.已知矩形ABCD,请找出相等的线段和相等的角. 试一试3.已知矩形ABCD,请找出所有的直角三角形和等腰三角形. 矩形的问题可以转化到直角三角形或等腰三角形来解决. Rt△ADC、 Rt△DCB、
Rt△DAB、 Rt△ABC、△ADO、 △DOC、
△COB、 △AOB、共同练习 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4cm,求矩形对角线的长. 矩形的问题可以转化到直角三角形或等腰(边)三角形的问题来解决. 变式:若BD=8cm,∠AOD=120°,求 边AB的长。OABCD公平,因为OB=OD = OA=OC投圈游戏OABCDOB=OD = OA=OC推论:直角三角形斜边上的中线等于
斜边的一半。
= AC= BD 在 中,∠ABC=900 ,BO是斜边AC上的中线
OB = AC推论:直角三角形斜边上的中线等于斜边的一半.已知△ABC中∠ACB=90°,AD = BD
求证:CD = AB证明:延长CD到E使DE=CD,
连结AE、BE.∵AD = BD , DE =CD
∴四边形ACBE是平行四边形E?练一练 已知△ABC是Rt△,∠ABC=900,BD是斜边AC上的中线.(1)若 BD=3㎝,则AC=______ ㎝;
(2)若 ∠C=30°,AB=5㎝,则AC=_____㎝,
BD=_____㎝.6510 学海 无涯3.在 中,斜边AC上的中线
和高分别是6cm和5cm,则 的
面积S=( )。 A
BCDE30cm21.如图1,在矩形ABCD中,E、F是AB上的两点,且AE=BF,则
∠ ADE与 巩固 练习DA E F BC图1∠ BCF相等吗?为什么?2.如图2,矩形ABCD的对角线AC和BD相交于点O,CE//BD,交AB的延长线于点E,求证:AC=EC.A DBECO图23.已知:如图,在四边形ABCD中,∠ABC=∠ADC=900,M是AC的中点,N是
反馈 练习(1)试判断MD与MB的大小关系。
(2)试判断MN与BD的位置关系。
BD的中点。用一用 某学校因地制宜:先向北量6m,再向东量8m,接着向南量6m,最后向西量8m,在圈出的这块空地上建一个草坪.(1)圈出的空地是什么形状?(2)考虑到护理草坪,学校购置了一台自动喷水器, 这台机器的最大喷水距离为5m,问这台机器能对整个草坪进行护理吗?若能,则喷水器应安放在何处;若不能,请说明理由.O矩形的四个角均为直角矩形的对角线互相平分且相等矩形的对边平行且相等6868课堂小结1.知识小结2.学法小结(1)用类比的方法探究矩形的性质,先找共性再找特殊性,
并注意性质的整合;(2)矩形的问题常可以转化为直角三角形或等腰三角形
的问题来解决. 矩形ABCD中,AB= 4,BC=2,E是边CD 上的一点,AE=AB.求∠BEC的度数.课后作业课后练习:
如图,BD、CE是△ABC的高,G 、 F
分别是BC、DE的中点,求证:FG DE.AEBGCDF例2:如图,△ABC中,∠ACB=900,点D、E分别为AC、AB的中点,点F在BC延长线上,且∠CDF=∠A,
求证:四边形DECF是平行四边形;四边形ABCD是矩形
若已知AB=8㎝,AD=6㎝,
则AC= ㎝ OB= ㎝
若已知∠CAB=40°,则∠OCB=
∠OBA= ∠AOB= ∠AOD=
若已知AC=10㎝,BC=6㎝,则矩形的周长= ㎝
矩形的面积= ㎝2
4 若已知 ∠DOC=120°,AD=6㎝,则AC= ㎝550°10100°40°12482880°试一试如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线的长是13cm,那么矩形的周长是多少?
练一练:书本P104:练习3练习:如图四边形ABCD中,∠ABC=∠ADC=900,E是AC中点,EF平分∠BED交BD于点F,
(1)猜想EF与BD具有怎样的关系?
(2)试证明你的猜想。
再见投圈游戏 三位学生正在做投圈游戏,他们分别站在一个直角三角形的三个顶点处,目标物放在斜边的中点处,这样的队形对每个人公平吗? 在直角三角形中斜边上的中线等于斜边的一半. (1)随着∠a的变化,两条对角线的长度怎
样变化的?(2)当∠a变为直角时,平行四边形成为一个矩形,这时它的其他内角是什么样的角?(3)当∠a是直角时,平行四边形变成矩形,此时
两条对角线的长度有什么关系?随着∠a的变化,一条对角线在变长,
一条在变短。都变为了直角两条对角线相等活动一设矩形的对角线AC与BD交于点E,那么,BE是Rt△ABC中一条怎样的特殊线段? 它与AC有什么大小关系?为什么?由此可得推论:
直角三角形斜边上的中线等于斜边的一半BE是Rt△ABC中斜边AC上的中线. BE等于AC的一半.∵ AC=BD,BE=DE,议一议:八年级 数学第十九章 四边形
