矩形(1)矩形的性质[下学期]
文档属性
| 名称 | 矩形(1)矩形的性质[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-05-13 00:00:00 | ||
图片预览







文档简介
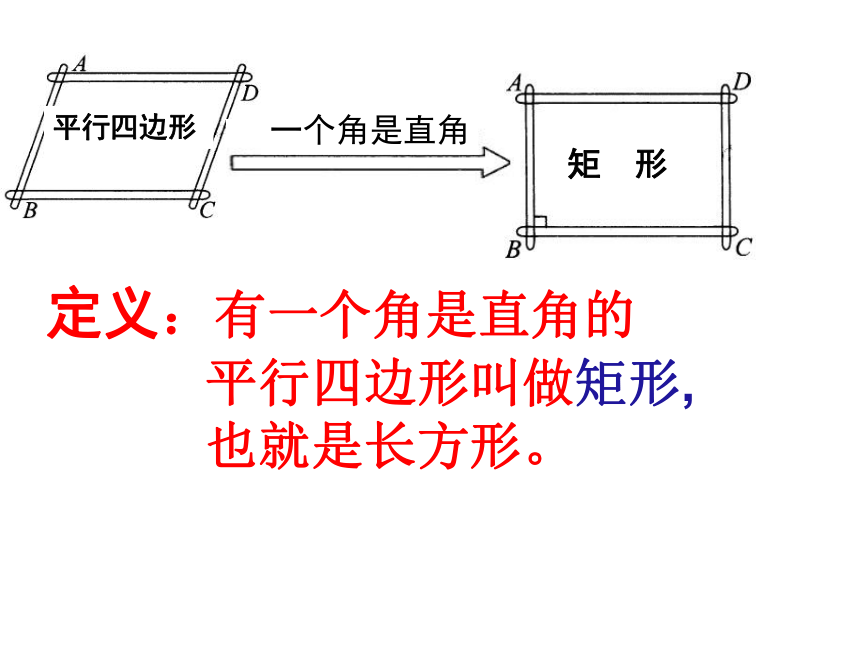
课件30张PPT。矩形矩形定义:有一个角是直角的
平行四边形叫做矩形,
也就是长方形。
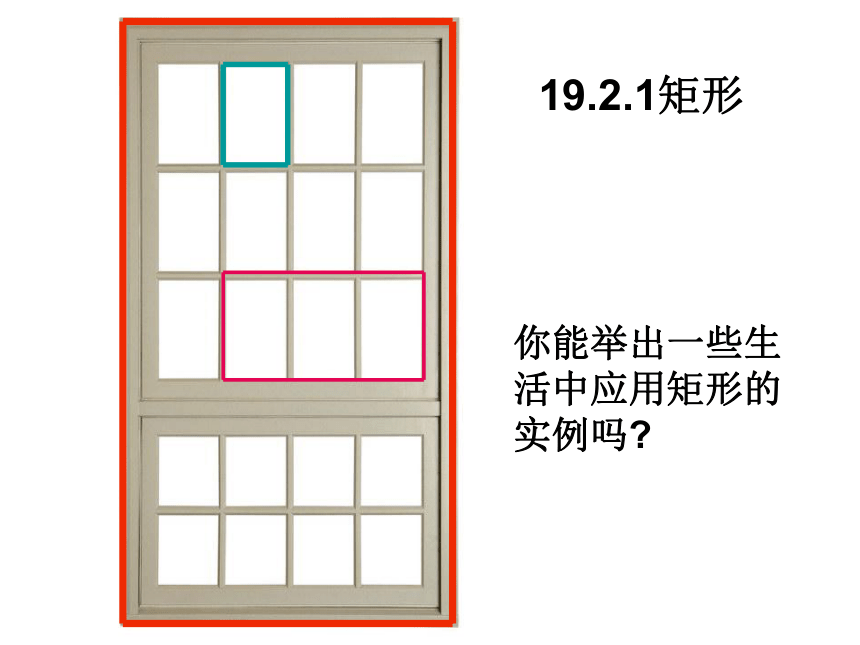
一个角是直角平行四边形矩 形一个角是直角有一个角是直角的平行四边形叫做矩形矩形的定义请欣赏19.2.1矩形你能举出一些生
活中应用矩形的
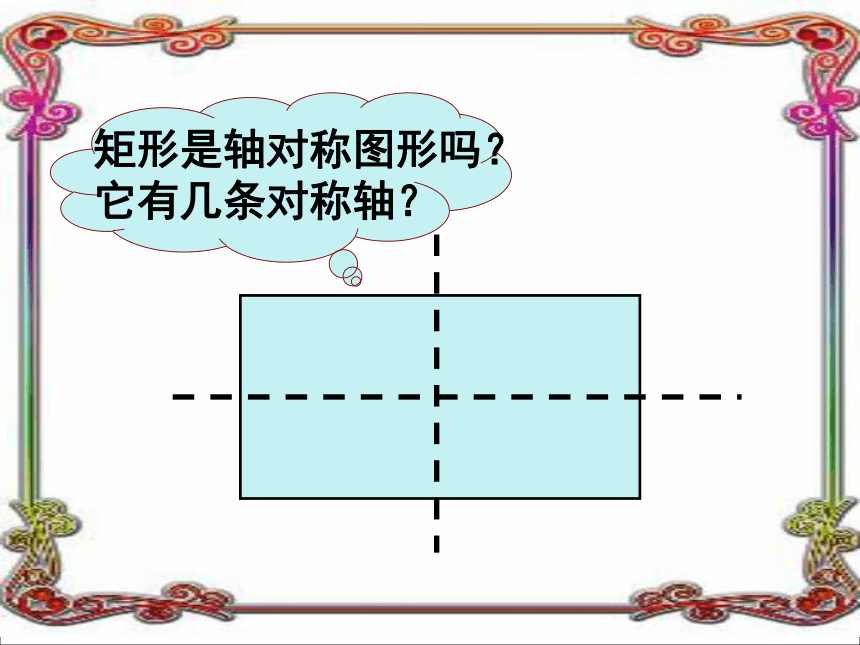
实例吗?矩形是轴对称图形吗?
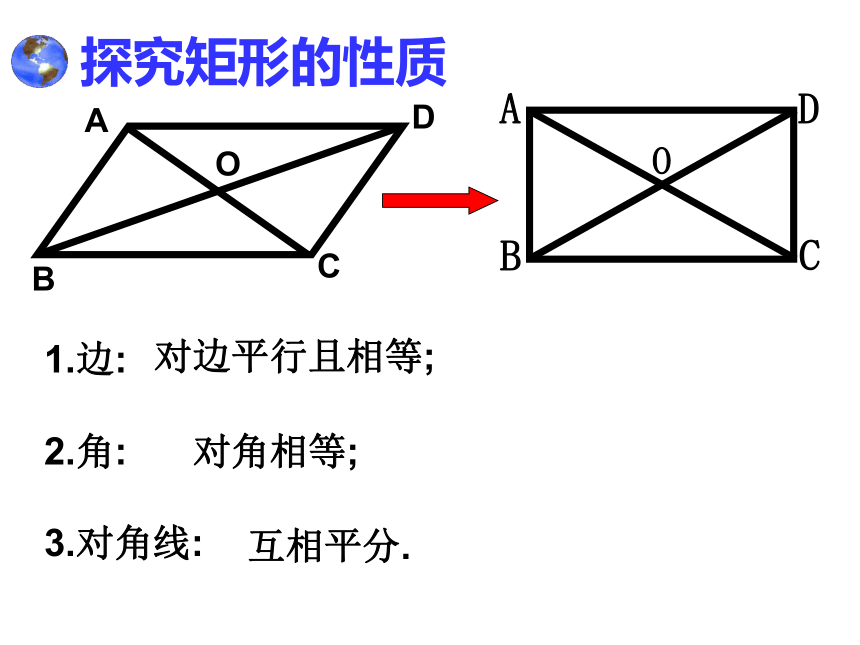
它有几条对称轴?探究 矩形的性质OAB1.边:
2.角:
3.对角线:CD对边平行且相等;对角相等;互相平分.O1.边:
2.角:
3.对角线:再看一遍1.边:
2.角:
3.对角线:∠BAD=∠BCD =∠ABC=∠ADC= 90°OOA=OC=OB=ODAB1.边:
2.角:
3.对角线:对边平行且相等;四个角都是直角;对角线相等且互相平分.CD已知:四边形ABCD是矩形,求证:AC = BD.证明:∵四边形ABCD是矩形∴∠ABC = ∠DCB = 90°∴△ABC≌△DCB(SAS) ∴AC = BD 2: 矩形的对角线相等.性质猜想在△ABC和△DCB中AB = DC AB = DC
∠ABC = ∠DCB
BC = CB1.矩形具有而一般平行四边形不具有的性质是( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分2.下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角相等
C.是轴对称图形 D.对角线互相垂直AD已知矩形ABCD,请找出所有的直角三角形和等腰三角形. 矩形的问题可以转化到直角三角形或等腰三角形来解决. Rt△ADC、 Rt△DCB、
Rt△DAB、 Rt△ABC、△ADO、 △DOC、
△COB、 △AOB、600如图,矩形ABCD的两条对角线相交于点O,AB=4cm,∠AOB=60°,求矩形对角线的长。解:∵四边形ABCD是矩形,∴AC与BD相等且互相平分。又 ∠AOB=60°,∴ ΔOAB是等边三角形∴OA=AB=4(cm)∴ AC=BD = 2OA=2×4=8(cm)
∴ OA = OB。变式:若BD=8cm,∠AOD=120°,求边AB的长。
O1200OABCD公平,因为OB=OD = OA=OC生活链接---投圈游戏OABCDOB=OD = OA=OC推论:直角三角形斜边上的中线等于
斜边的一半。
= AC= BD 在 中,∠ABC=900 ,BO是斜边AC上的中线
OB = AC已知:在△ABC中∠ACB=90°,AD = BD证明:延长CD到E使DE=CD,连 结AE、BE.∵AD = BD ,CD = EDE∴ACBE是平行四边形又∵∠ACB = 90∴CE = AB 1. 已知△ABC是Rt△,∠ABC=900,BD是斜边AC上的中线.(1)若BD=3㎝,则AC=______ ㎝;
(2)若∠C=30°,AB=5㎝,则AC=_____㎝,
BD=_____㎝.6510A2.在 中,斜边AC上的中线
和高分别是6cm和5cm,则 的
面积S=( )。 A
BCDE30cm2D3.在Rt⊿ABC中,∠C=90°,
AB=2AC.
求∠ A 、 ∠B 的度数.作斜边AB边的中线又∵AB=2AC∴⊿ACD是等边三角形∴∠A=60°
∴∠B=30 °练习4.矩形ABCD中,AB=2BC,AE=AB,求∠EBC的度数ABCDE5.设矩形ABCD和矩形AEFC的面积分别为S1、S2,则二者的大小关系是:S1________S2.6.已知如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=1200,求∠EAO的度数和∠OEA的度数 。7.已知:如图,在四边形ABCD中,∠ABC=∠ADC=900,M是AC的中点,N是
(1)试判断MD与MB的大小关系。
(2)试判断MN与BD的位置关系。
BD的中点。本课小结矩形的四个角都是直角.※ 矩形的定义:
一个角是直角的平行四边形是矩形 矩形的对角线相等.※ 矩形的性质※ 推 论 直角三角形斜边上的中线等于斜边的一半.同学们再见
平行四边形叫做矩形,
也就是长方形。
一个角是直角平行四边形矩 形一个角是直角有一个角是直角的平行四边形叫做矩形矩形的定义请欣赏19.2.1矩形你能举出一些生
活中应用矩形的
实例吗?矩形是轴对称图形吗?
它有几条对称轴?探究 矩形的性质OAB1.边:
2.角:
3.对角线:CD对边平行且相等;对角相等;互相平分.O1.边:
2.角:
3.对角线:再看一遍1.边:
2.角:
3.对角线:∠BAD=∠BCD =∠ABC=∠ADC= 90°OOA=OC=OB=ODAB1.边:
2.角:
3.对角线:对边平行且相等;四个角都是直角;对角线相等且互相平分.CD已知:四边形ABCD是矩形,求证:AC = BD.证明:∵四边形ABCD是矩形∴∠ABC = ∠DCB = 90°∴△ABC≌△DCB(SAS) ∴AC = BD 2: 矩形的对角线相等.性质猜想在△ABC和△DCB中AB = DC AB = DC
∠ABC = ∠DCB
BC = CB1.矩形具有而一般平行四边形不具有的性质是( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分2.下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角相等
C.是轴对称图形 D.对角线互相垂直AD已知矩形ABCD,请找出所有的直角三角形和等腰三角形. 矩形的问题可以转化到直角三角形或等腰三角形来解决. Rt△ADC、 Rt△DCB、
Rt△DAB、 Rt△ABC、△ADO、 △DOC、
△COB、 △AOB、600如图,矩形ABCD的两条对角线相交于点O,AB=4cm,∠AOB=60°,求矩形对角线的长。解:∵四边形ABCD是矩形,∴AC与BD相等且互相平分。又 ∠AOB=60°,∴ ΔOAB是等边三角形∴OA=AB=4(cm)∴ AC=BD = 2OA=2×4=8(cm)
∴ OA = OB。变式:若BD=8cm,∠AOD=120°,求边AB的长。
O1200OABCD公平,因为OB=OD = OA=OC生活链接---投圈游戏OABCDOB=OD = OA=OC推论:直角三角形斜边上的中线等于
斜边的一半。
= AC= BD 在 中,∠ABC=900 ,BO是斜边AC上的中线
OB = AC已知:在△ABC中∠ACB=90°,AD = BD证明:延长CD到E使DE=CD,连 结AE、BE.∵AD = BD ,CD = EDE∴ACBE是平行四边形又∵∠ACB = 90∴CE = AB 1. 已知△ABC是Rt△,∠ABC=900,BD是斜边AC上的中线.(1)若BD=3㎝,则AC=______ ㎝;
(2)若∠C=30°,AB=5㎝,则AC=_____㎝,
BD=_____㎝.6510A2.在 中,斜边AC上的中线
和高分别是6cm和5cm,则 的
面积S=( )。 A
BCDE30cm2D3.在Rt⊿ABC中,∠C=90°,
AB=2AC.
求∠ A 、 ∠B 的度数.作斜边AB边的中线又∵AB=2AC∴⊿ACD是等边三角形∴∠A=60°
∴∠B=30 °练习4.矩形ABCD中,AB=2BC,AE=AB,求∠EBC的度数ABCDE5.设矩形ABCD和矩形AEFC的面积分别为S1、S2,则二者的大小关系是:S1________S2.6.已知如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=1200,求∠EAO的度数和∠OEA的度数 。7.已知:如图,在四边形ABCD中,∠ABC=∠ADC=900,M是AC的中点,N是
(1)试判断MD与MB的大小关系。
(2)试判断MN与BD的位置关系。
BD的中点。本课小结矩形的四个角都是直角.※ 矩形的定义:
一个角是直角的平行四边形是矩形 矩形的对角线相等.※ 矩形的性质※ 推 论 直角三角形斜边上的中线等于斜边的一半.同学们再见
