【质量检测卷】人教版数学九年级上册 第二十四章质量评价(教师版)
文档属性
| 名称 | 【质量检测卷】人教版数学九年级上册 第二十四章质量评价(教师版) | 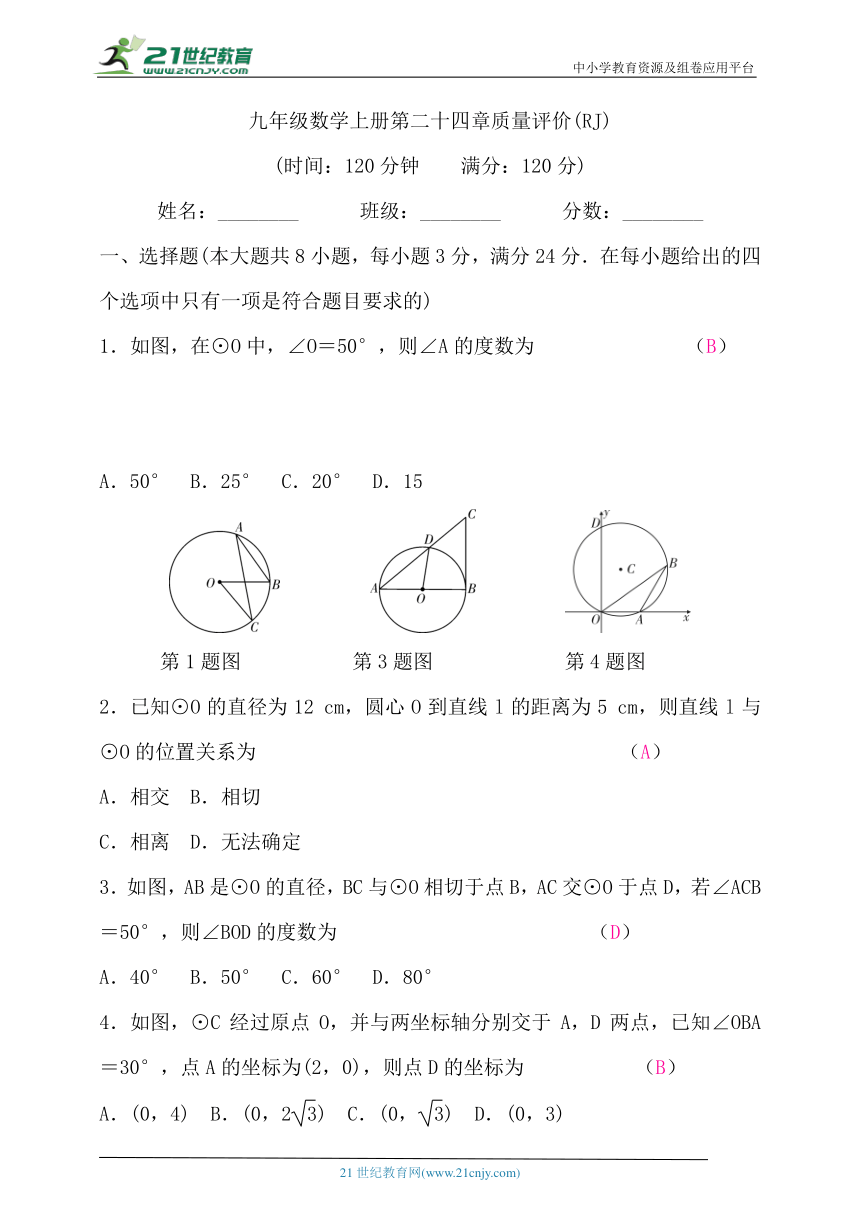 | |
| 格式 | DOC | ||
| 文件大小 | 494.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-08 13:51:24 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
九年级数学上册第二十四章质量评价(RJ)
(时间:120分钟 满分:120分)
姓名:________ 班级:________ 分数:________
一、选择题(本大题共8小题,每小题3分,满分24分.在每小题给出的四个选项中只有一项是符合题目要求的)
1.如图,在⊙O中,∠O=50°,则∠A的度数为 (B)
A.50° B.25° C.20° D.15
第1题图 第3题图 第4题图
2.已知⊙O的直径为12 cm,圆心O到直线l的距离为5 cm,则直线l与⊙O的位置关系为 (A)
A.相交 B.相切
C.相离 D.无法确定
3.如图,AB是⊙O的直径,BC与⊙O相切于点B,AC交⊙O于点D,若∠ACB=50°,则∠BOD的度数为 (D)
A.40° B.50° C.60° D.80°
4.如图,⊙C经过原点O,并与两坐标轴分别交于A,D两点,已知∠OBA=30°,点A的坐标为(2,0),则点D的坐标为 (B)
A.(0,4) B.(0,2) C.(0,) D.(0,3)
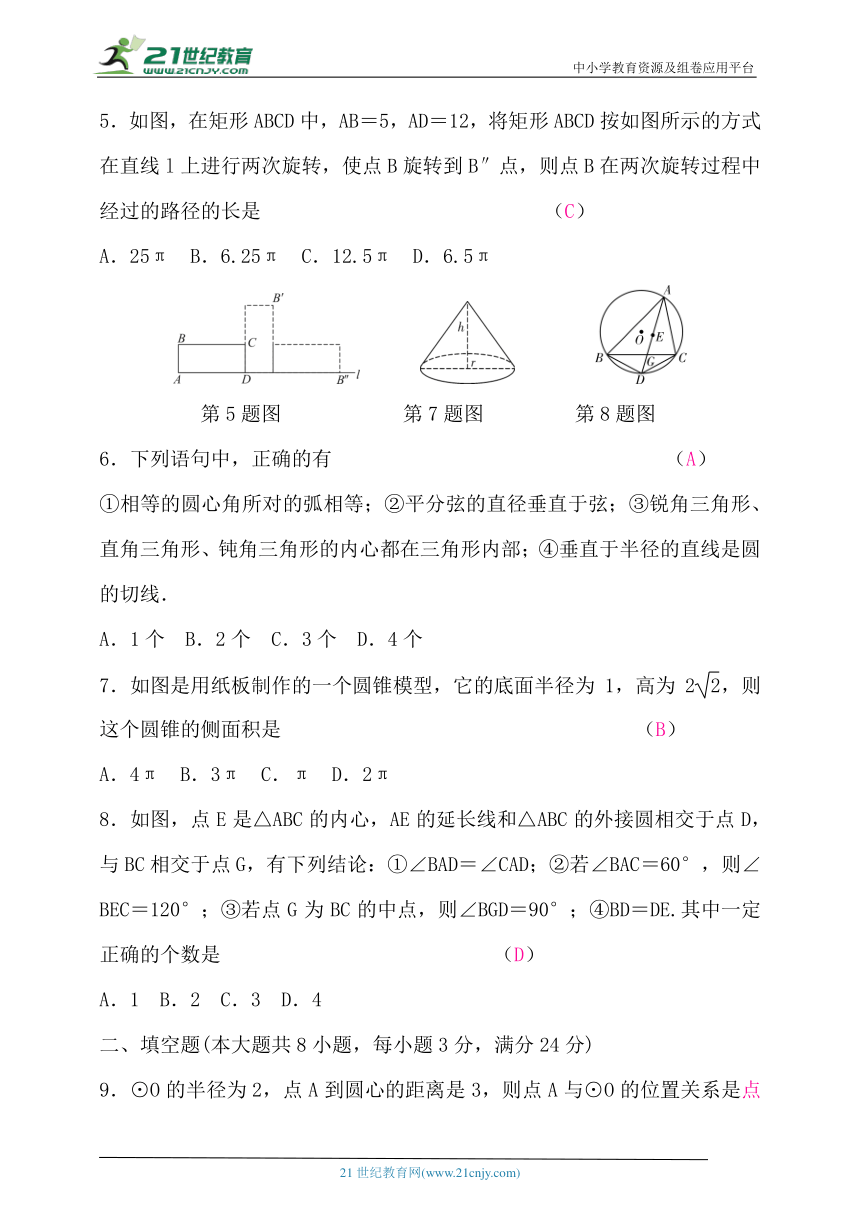
5.如图,在矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线l上进行两次旋转,使点B旋转到B″点,则点B在两次旋转过程中经过的路径的长是 (C)
A.25π B.6.25π C.12.5π D.6.5π
第5题图 第7题图 第8题图
6.下列语句中,正确的有 (A)
①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦;③锐角三角形、直角三角形、钝角三角形的内心都在三角形内部;④垂直于半径的直线是圆的切线.
A.1个 B.2个 C.3个 D.4个
7.如图是用纸板制作的一个圆锥模型,它的底面半径为1,高为2,则这个圆锥的侧面积是 (B)
A.4π B.3π C.π D.2π
8.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,与BC相交于点G,有下列结论:①∠BAD=∠CAD;②若∠BAC=60°,则∠BEC=120°;③若点G为BC的中点,则∠BGD=90°;④BD=DE.其中一定正确的个数是 (D)
A.1 B.2 C.3 D.4
二、填空题(本大题共8小题,每小题3分,满分24分)
9.⊙O的半径为2,点A到圆心的距离是3,则点A与⊙O的位置关系是点A在⊙O外.
10.已知扇形OAB的半径是5,圆心角是72°,则此扇形的面积是5π.
11.△ABC内接于半径为5 cm的⊙O,且∠BAC=30°,则BC的长为5cm.
12.一个直角三角形的两条直角边长是方程x2-7x+12=0的两个根,则此直角三角形的内切圆的半径为1.
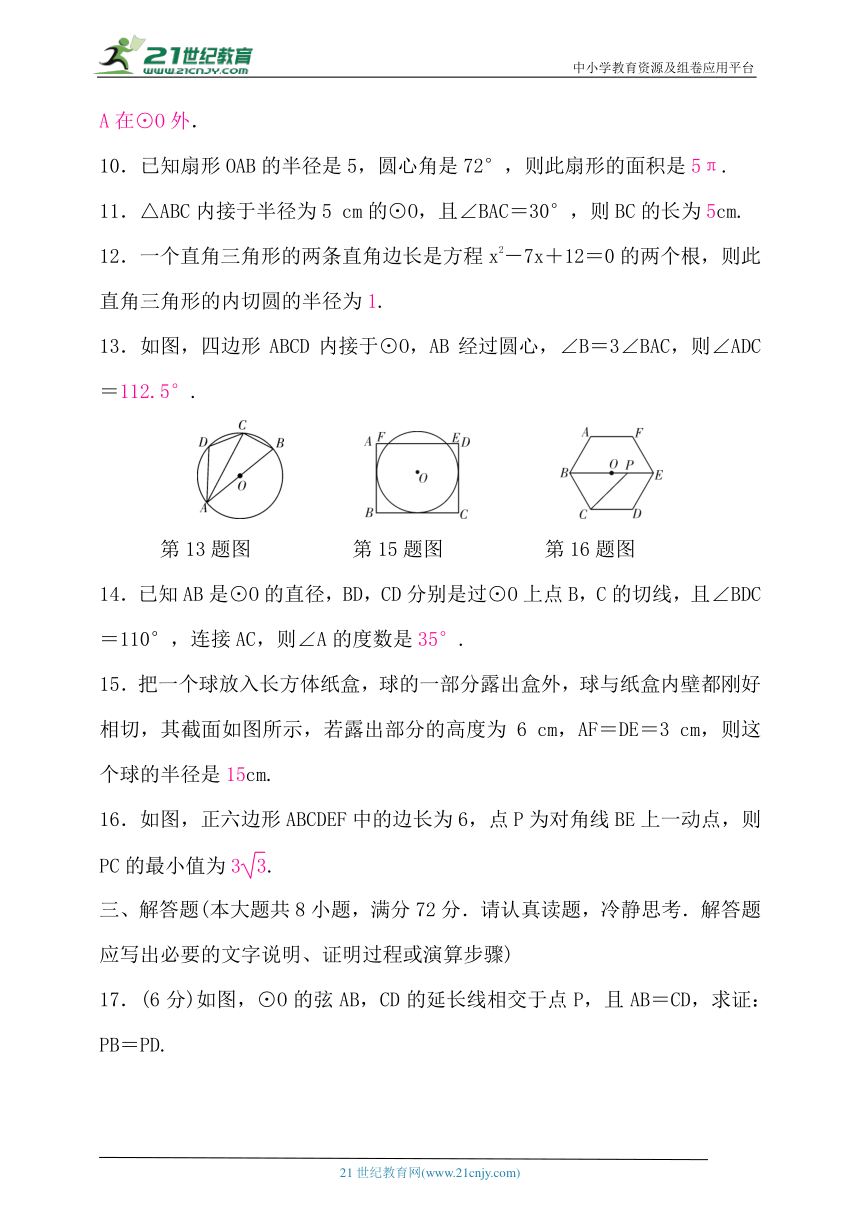
13.如图,四边形ABCD内接于⊙O,AB经过圆心,∠B=3∠BAC,则∠ADC=112.5°.
第13题图 第15题图 第16题图
14.已知AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=110°,连接AC,则∠A的度数是35°.
15.把一个球放入长方体纸盒,球的一部分露出盒外,球与纸盒内壁都刚好相切,其截面如图所示,若露出部分的高度为6 cm,AF=DE=3 cm,则这个球的半径是15cm.
16.如图,正六边形ABCDEF中的边长为6,点P为对角线BE上一动点,则PC的最小值为3.
三、解答题(本大题共8小题,满分72分.请认真读题,冷静思考.解答题应写出必要的文字说明、证明过程或演算步骤)
17.(6分)如图,⊙O的弦AB,CD的延长线相交于点P,且AB=CD,求证:PB=PD.
证明:连接AC,
∵AB=CD,
∴=,∴+=+.
即=,
∴∠A=∠C,∴PA=PC,
∴PA-AB=PC-CD.
即PB=PD.
18.(8分)如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)若∠AOC=40°,求∠DEB的度数;
(2)若OC=3,OA=5,求AB的长.
解:(1)∵AB是⊙O的一条弦,OD⊥AB,
∴=.∴∠DEB=∠AOD=×40°=20°.
(2)∵AB是⊙O的一条弦,OD⊥AB,∴AC=BC,即AB=2AC.
在Rt△AOC中,∵AC==4.∴AB=8.
19.(8分)如图,AB为⊙O的弦,BD切⊙O于点B,OD⊥OA,OD与AB相交于点C.求证:BD=CD.
证明:连接OB,∵BD切⊙O于点B,∴OB⊥BD,
∴∠1+∠2=90°,∵OD⊥OA,∴∠AOC=90°,
∴∠A+∠4=90°,
∵OA=OB,∴∠1=∠A,∴∠2=∠4,而∠3=∠4,
∴∠2=∠3,∴BD=CD.
20.(9分)如图,AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连接BC.
(1)求证:AE=ED;
(2)若AB=10,∠CBD=36°,求的长及扇形AOC的面积.
(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∵OC∥BD,∴∠AEO=∠ADB=90°,
即OC⊥AD,∴AE=ED.
(2)解:∵OC⊥AD,
∴=,∴∠AOC=72°,
∴==2π,S扇形AOC==5π.
21.(9分)如图,AB是⊙O的直径,C是的中点,CE⊥AB,垂足为E,BD交CE于点F.
(1)求证:CF=BF;
(2)若AD=6,⊙O的半径为5,求BC的长.
(1)证明:连接AC,
∵C是的中点,∴∠DBC=∠BAC,
∵∠BCE+∠ECA=∠BAC+∠ECA=90°,
∴∠BCE=∠BAC,∴∠BCE=∠DBC,
∴CF=BF.
(2)解:连接OC交BD于点G,
∵AB是⊙O的直径,
∴∠ADB=90°,AB=2OC=10,
∴BD=8,∵C是的中点,
∴OC⊥BD,DG=BG=BD=4,
∵OA=OB,∴OG是△ABD的中位线,
∴OG=AD=3,
∴CG=OC-OG=5-3=2,
在Rt△BCG中,由勾股定理得BC=2.
22.(10分)如图,AB是⊙O的直径,C是⊙O上的点,点D在AB的延长线上,∠BCD=∠BAC.
(1)求证:CD是⊙O的切线;
(2)若∠D=30°,BD=2,求图中阴影部分的面积.
(1)证明:连接OC,
∵OA=OC,∴∠BAC=∠OCA,
∵∠BCD=∠BAC,∴∠BCD=∠OCA,
∵AB是直径,∴∠ACB=90°,
∴∠OCA+∠OCB=∠BCD+∠OCB=90°,
∴∠OCD=90°,
∵OC是半径,∴CD是⊙O的切线.
(2)解:设⊙O的半径为r,∴AB=2r,
∵∠D=30°,∠OCD=90°,∴OD=2r,∠COB=60°,
∴r+2=2r,∴r=2,∠AOC=120°,∴BC=2,由勾股定理得AC=2,
易求S△AOC=×2×1=.S扇形OAC==,
∴阴影部分的面积为π-.
23.(10分)如图,已知Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,O是AB边上一点,⊙O经过点B,D,与AB交于点E.
(1)求证:AC是⊙O的切线;
(2)若BC=3,AC=4,求AE的长.
(1)证明:连接OD,
∵OB=OD,∴∠ODB=∠OBD,
∵BD平分∠ABC,∴∠OBD=∠CBD,
∴∠ODB=∠CBD,∴OD∥BC,
∴∠ADO=∠C=90°,∴OD⊥AC,
∵OD为⊙O的半径,∴AC是⊙O的切线.
(2)解:∵∠C=90°,BC=3,AC=4,∴AB=5,
作DF⊥AB于点F,则△BDC≌△BDF(AAS),
∴BF=BC=3,AF=AB-BF=2.设DF=DC=x,
在Rt△ADF中,AF2+DF2=AD2,
∴(4-x)2=22+x2,解得x=1.5,∴AD=2.5.
∵OA·DF=OD·AD,
设⊙O的半径是r,则有(5-r)×1.5=r×2.5,解得r=.
∴AE=AB-BE=.
24.(12分)如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,与AC,BC分别交于点M,N,与AB的另一个交点为E.过点N作NF⊥AB,垂足为F.
(1)求证:NF是⊙O的切线;
(2)若NF=2,DF=1,求弦ED的长.
(1)证明:连接ON.
∵在Rt△ACB中,CD是边AB的中线,
∴CD=BD,∴∠DCB=∠B,
∵OC=ON,
∴∠ONC=∠DCB,
∴∠ONC=∠B,∴ON∥AB.
∵NF⊥AB,∴∠NFB=90°.
∴∠ONF=∠NFB=90°,∴ON⊥NF.
又∵NF过半径ON的外端,
∴NF是⊙O的切线.
(2)解:过点O作OH⊥ED,垂足为H,
设⊙O的半径为r,
∵OH⊥ED,NF⊥AB,ON⊥NF,
∴∠OHD=∠NFH=∠ONF=90°.
∴四边形ONFH为矩形.
∴HF=ON=r,OH=NF=2,
∴HD=HF-DF=r-1,
在Rt△OHD中,∠OHD=90°,
∴OH2+HD2=OD2,
即22+(r-1)2=r2,∴r=.∴HD=,
∵OH⊥ED,且OH过圆心O,
∴HE=HD,
∴ED=2HD=3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
九年级数学上册第二十四章质量评价(RJ)
(时间:120分钟 满分:120分)
姓名:________ 班级:________ 分数:________
一、选择题(本大题共8小题,每小题3分,满分24分.在每小题给出的四个选项中只有一项是符合题目要求的)
1.如图,在⊙O中,∠O=50°,则∠A的度数为 (B)
A.50° B.25° C.20° D.15
第1题图 第3题图 第4题图
2.已知⊙O的直径为12 cm,圆心O到直线l的距离为5 cm,则直线l与⊙O的位置关系为 (A)
A.相交 B.相切
C.相离 D.无法确定
3.如图,AB是⊙O的直径,BC与⊙O相切于点B,AC交⊙O于点D,若∠ACB=50°,则∠BOD的度数为 (D)
A.40° B.50° C.60° D.80°
4.如图,⊙C经过原点O,并与两坐标轴分别交于A,D两点,已知∠OBA=30°,点A的坐标为(2,0),则点D的坐标为 (B)
A.(0,4) B.(0,2) C.(0,) D.(0,3)
5.如图,在矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线l上进行两次旋转,使点B旋转到B″点,则点B在两次旋转过程中经过的路径的长是 (C)
A.25π B.6.25π C.12.5π D.6.5π
第5题图 第7题图 第8题图
6.下列语句中,正确的有 (A)
①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦;③锐角三角形、直角三角形、钝角三角形的内心都在三角形内部;④垂直于半径的直线是圆的切线.
A.1个 B.2个 C.3个 D.4个
7.如图是用纸板制作的一个圆锥模型,它的底面半径为1,高为2,则这个圆锥的侧面积是 (B)
A.4π B.3π C.π D.2π
8.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,与BC相交于点G,有下列结论:①∠BAD=∠CAD;②若∠BAC=60°,则∠BEC=120°;③若点G为BC的中点,则∠BGD=90°;④BD=DE.其中一定正确的个数是 (D)
A.1 B.2 C.3 D.4
二、填空题(本大题共8小题,每小题3分,满分24分)
9.⊙O的半径为2,点A到圆心的距离是3,则点A与⊙O的位置关系是点A在⊙O外.
10.已知扇形OAB的半径是5,圆心角是72°,则此扇形的面积是5π.
11.△ABC内接于半径为5 cm的⊙O,且∠BAC=30°,则BC的长为5cm.
12.一个直角三角形的两条直角边长是方程x2-7x+12=0的两个根,则此直角三角形的内切圆的半径为1.
13.如图,四边形ABCD内接于⊙O,AB经过圆心,∠B=3∠BAC,则∠ADC=112.5°.
第13题图 第15题图 第16题图
14.已知AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=110°,连接AC,则∠A的度数是35°.
15.把一个球放入长方体纸盒,球的一部分露出盒外,球与纸盒内壁都刚好相切,其截面如图所示,若露出部分的高度为6 cm,AF=DE=3 cm,则这个球的半径是15cm.
16.如图,正六边形ABCDEF中的边长为6,点P为对角线BE上一动点,则PC的最小值为3.
三、解答题(本大题共8小题,满分72分.请认真读题,冷静思考.解答题应写出必要的文字说明、证明过程或演算步骤)
17.(6分)如图,⊙O的弦AB,CD的延长线相交于点P,且AB=CD,求证:PB=PD.
证明:连接AC,
∵AB=CD,
∴=,∴+=+.
即=,
∴∠A=∠C,∴PA=PC,
∴PA-AB=PC-CD.
即PB=PD.
18.(8分)如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)若∠AOC=40°,求∠DEB的度数;
(2)若OC=3,OA=5,求AB的长.
解:(1)∵AB是⊙O的一条弦,OD⊥AB,
∴=.∴∠DEB=∠AOD=×40°=20°.
(2)∵AB是⊙O的一条弦,OD⊥AB,∴AC=BC,即AB=2AC.
在Rt△AOC中,∵AC==4.∴AB=8.
19.(8分)如图,AB为⊙O的弦,BD切⊙O于点B,OD⊥OA,OD与AB相交于点C.求证:BD=CD.
证明:连接OB,∵BD切⊙O于点B,∴OB⊥BD,
∴∠1+∠2=90°,∵OD⊥OA,∴∠AOC=90°,
∴∠A+∠4=90°,
∵OA=OB,∴∠1=∠A,∴∠2=∠4,而∠3=∠4,
∴∠2=∠3,∴BD=CD.
20.(9分)如图,AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连接BC.
(1)求证:AE=ED;
(2)若AB=10,∠CBD=36°,求的长及扇形AOC的面积.
(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∵OC∥BD,∴∠AEO=∠ADB=90°,
即OC⊥AD,∴AE=ED.
(2)解:∵OC⊥AD,
∴=,∴∠AOC=72°,
∴==2π,S扇形AOC==5π.
21.(9分)如图,AB是⊙O的直径,C是的中点,CE⊥AB,垂足为E,BD交CE于点F.
(1)求证:CF=BF;
(2)若AD=6,⊙O的半径为5,求BC的长.
(1)证明:连接AC,
∵C是的中点,∴∠DBC=∠BAC,
∵∠BCE+∠ECA=∠BAC+∠ECA=90°,
∴∠BCE=∠BAC,∴∠BCE=∠DBC,
∴CF=BF.
(2)解:连接OC交BD于点G,
∵AB是⊙O的直径,
∴∠ADB=90°,AB=2OC=10,
∴BD=8,∵C是的中点,
∴OC⊥BD,DG=BG=BD=4,
∵OA=OB,∴OG是△ABD的中位线,
∴OG=AD=3,
∴CG=OC-OG=5-3=2,
在Rt△BCG中,由勾股定理得BC=2.
22.(10分)如图,AB是⊙O的直径,C是⊙O上的点,点D在AB的延长线上,∠BCD=∠BAC.
(1)求证:CD是⊙O的切线;
(2)若∠D=30°,BD=2,求图中阴影部分的面积.
(1)证明:连接OC,
∵OA=OC,∴∠BAC=∠OCA,
∵∠BCD=∠BAC,∴∠BCD=∠OCA,
∵AB是直径,∴∠ACB=90°,
∴∠OCA+∠OCB=∠BCD+∠OCB=90°,
∴∠OCD=90°,
∵OC是半径,∴CD是⊙O的切线.
(2)解:设⊙O的半径为r,∴AB=2r,
∵∠D=30°,∠OCD=90°,∴OD=2r,∠COB=60°,
∴r+2=2r,∴r=2,∠AOC=120°,∴BC=2,由勾股定理得AC=2,
易求S△AOC=×2×1=.S扇形OAC==,
∴阴影部分的面积为π-.
23.(10分)如图,已知Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,O是AB边上一点,⊙O经过点B,D,与AB交于点E.
(1)求证:AC是⊙O的切线;
(2)若BC=3,AC=4,求AE的长.
(1)证明:连接OD,
∵OB=OD,∴∠ODB=∠OBD,
∵BD平分∠ABC,∴∠OBD=∠CBD,
∴∠ODB=∠CBD,∴OD∥BC,
∴∠ADO=∠C=90°,∴OD⊥AC,
∵OD为⊙O的半径,∴AC是⊙O的切线.
(2)解:∵∠C=90°,BC=3,AC=4,∴AB=5,
作DF⊥AB于点F,则△BDC≌△BDF(AAS),
∴BF=BC=3,AF=AB-BF=2.设DF=DC=x,
在Rt△ADF中,AF2+DF2=AD2,
∴(4-x)2=22+x2,解得x=1.5,∴AD=2.5.
∵OA·DF=OD·AD,
设⊙O的半径是r,则有(5-r)×1.5=r×2.5,解得r=.
∴AE=AB-BE=.
24.(12分)如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,与AC,BC分别交于点M,N,与AB的另一个交点为E.过点N作NF⊥AB,垂足为F.
(1)求证:NF是⊙O的切线;
(2)若NF=2,DF=1,求弦ED的长.
(1)证明:连接ON.
∵在Rt△ACB中,CD是边AB的中线,
∴CD=BD,∴∠DCB=∠B,
∵OC=ON,
∴∠ONC=∠DCB,
∴∠ONC=∠B,∴ON∥AB.
∵NF⊥AB,∴∠NFB=90°.
∴∠ONF=∠NFB=90°,∴ON⊥NF.
又∵NF过半径ON的外端,
∴NF是⊙O的切线.
(2)解:过点O作OH⊥ED,垂足为H,
设⊙O的半径为r,
∵OH⊥ED,NF⊥AB,ON⊥NF,
∴∠OHD=∠NFH=∠ONF=90°.
∴四边形ONFH为矩形.
∴HF=ON=r,OH=NF=2,
∴HD=HF-DF=r-1,
在Rt△OHD中,∠OHD=90°,
∴OH2+HD2=OD2,
即22+(r-1)2=r2,∴r=.∴HD=,
∵OH⊥ED,且OH过圆心O,
∴HE=HD,
∴ED=2HD=3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
