人教版八年级数学上册13.4课题学习 最短路径问题 同步练习 (含答案)
文档属性
| 名称 | 人教版八年级数学上册13.4课题学习 最短路径问题 同步练习 (含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 149.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-05 00:00:00 | ||
图片预览

文档简介
13.4课题学习 最短路径问题
一、单选题
1.在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是100°,那么在△ABC中与这100°角对应相等的角是 ( )
A.∠A B.∠B C.∠C D.∠B或∠C
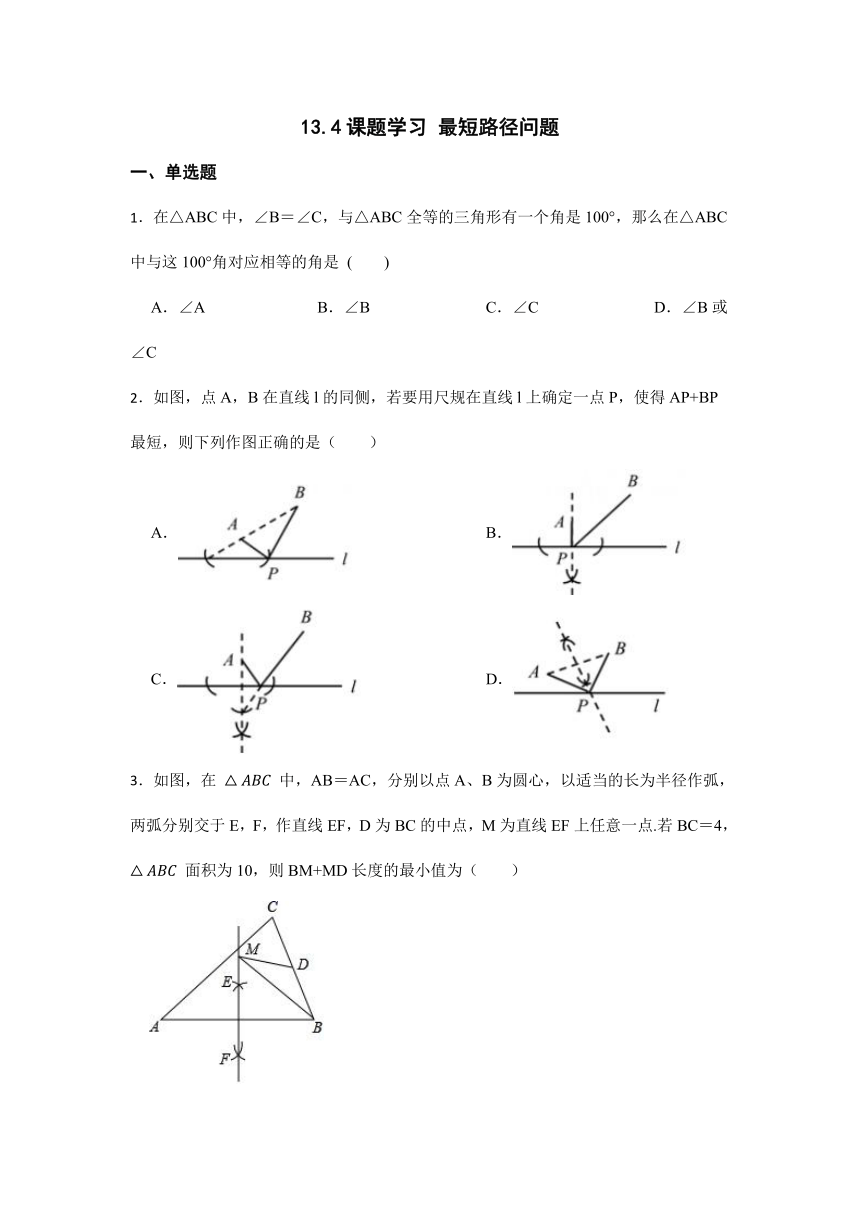
2.如图,点A,B在直线l的同侧,若要用尺规在直线l上确定一点P,使得AP+BP最短,则下列作图正确的是( )
A. B.
C. D.
3.如图,在 中,AB=AC,分别以点A、B为圆心,以适当的长为半径作弧,两弧分别交于E,F,作直线EF,D为BC的中点,M为直线EF上任意一点.若BC=4, 面积为10,则BM+MD长度的最小值为( )
A. B.3 C.4 D.5
4.在△ABC中,已知AB=7,点C到AB的距离为4,则△ABC周长的最小值是( )
A.5+4 B.+7 C.2+ D.以上都不对
5.如图,在平面直角坐标系中,已知A(1,1)、B(3,5),要在y轴上找一点P,使得△PAB的周长最小,则点P的坐标为( )
A.(0,1) B.(0,2) C.( ,0) D.(2,0)
6.如图,在△ 中, , 、 分别是底边 和腰 上的中线,点 为 上一动点,则 的最小值等于( )
A.线段 的长 B.线段 的长
C.线段 的长 D.线段 的长
二、填空题
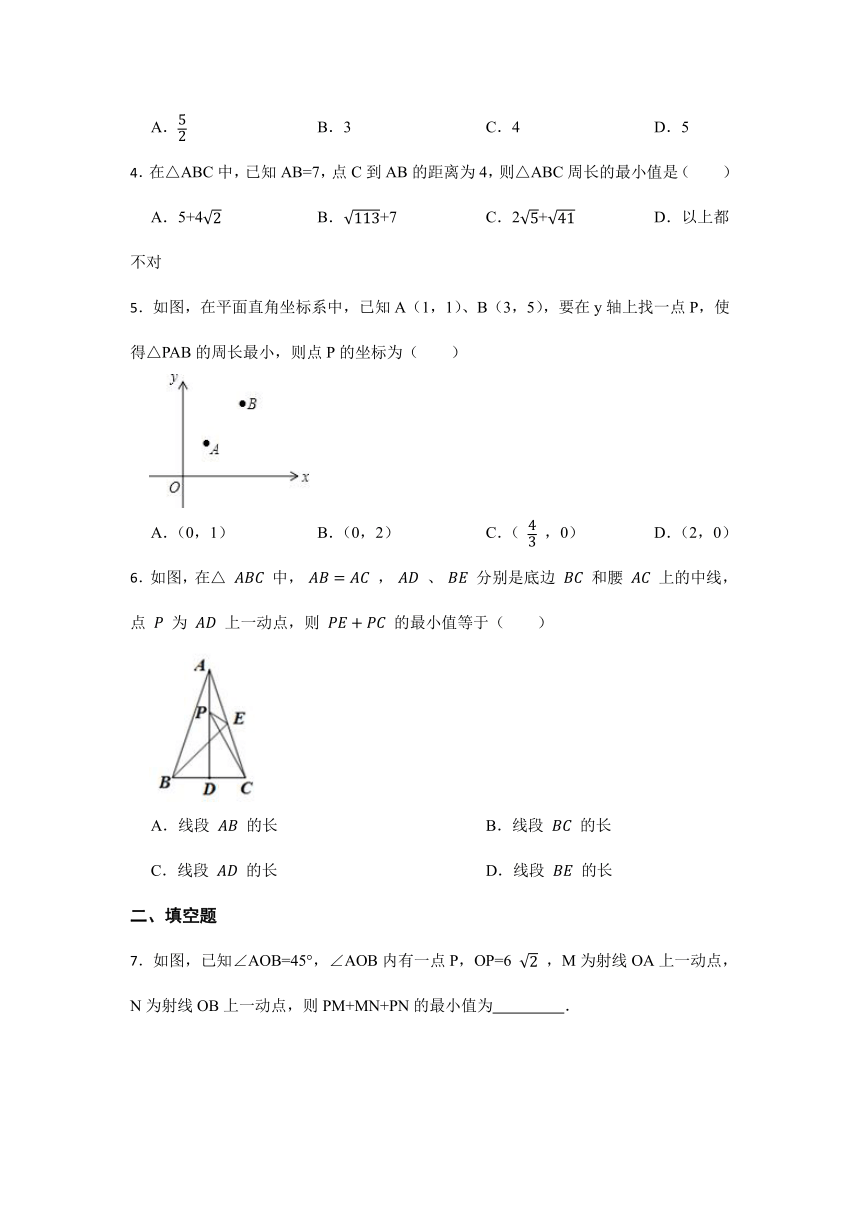
7.如图,已知∠AOB=45°,∠AOB内有一点P,OP=6 ,M为射线OA上一动点,N为射线OB上一动点,则PM+MN+PN的最小值为 .
8.如图,已知直线 y= x+3 与 x 轴、y 轴分别交于点 A、B,线段 AB 为直角边在第一内作等腰 Rt△ABC,∠BAC=90 . 点 P 是 x 轴上的一个动点,设 P(x,0).
(1)当 x = 时,PB+PC 的值最小;
(2)当 x = 时,|PB-PC|的值最大.
9.如图,等边△ABC中,AB=4,E是线段AC上的任意一点,∠BAC的平分线交BC于D,AD=2 ,F是AD上的动点,连接CF、EF,则CF+EF的最小值为 .
10.如图,在△ABC中,∠ACB=90°,AC=BC=4,D为BC中点,E为AB边上的动点,则△CDE周长的最小值为 .
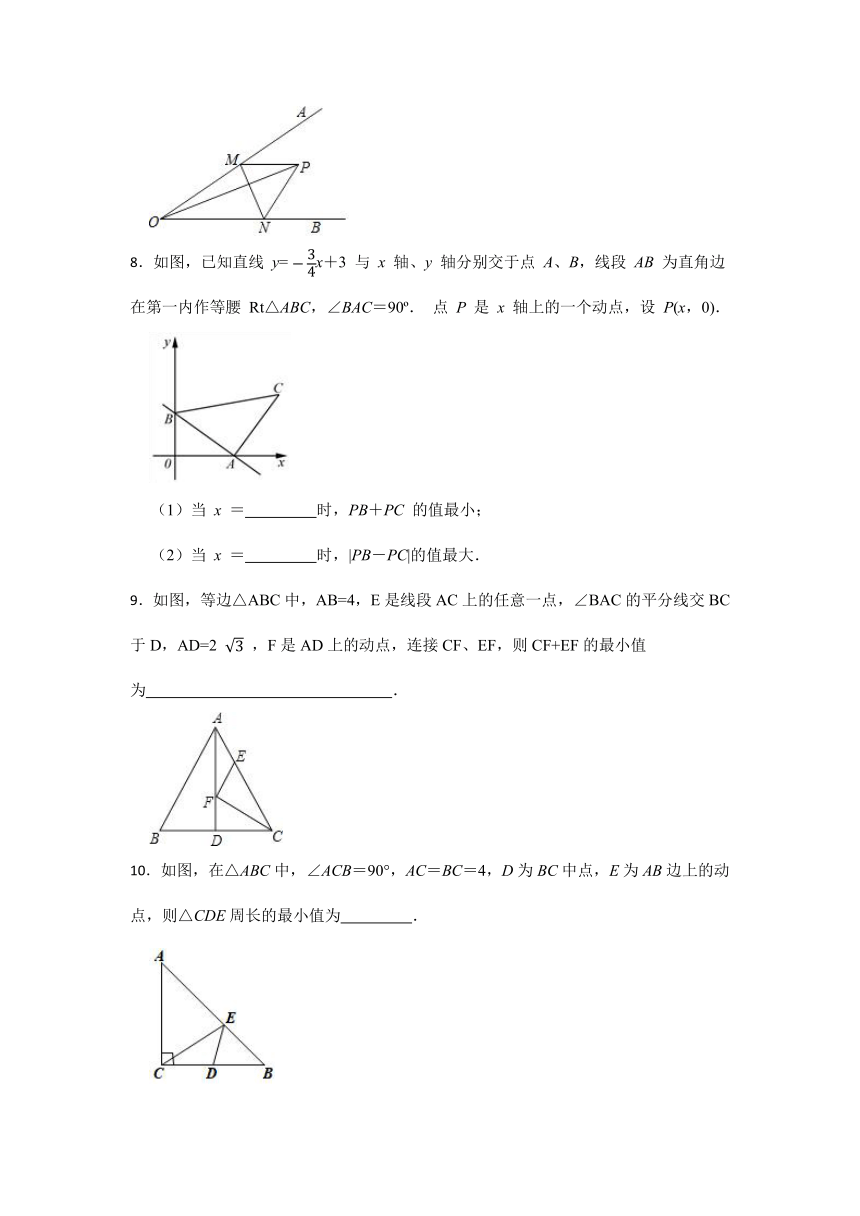
11.已知△ABC的面积是12,AB=AC=5,AD是BC边上的中线,E,P分别是AC,AD上的动点,则CP+EP的最小值为 .
12.如图,∠AOB=45°,OC平分∠AOB,点M为OB上一定点,P为OC上的一动点,N为OB上一动点,当PM+PN最小时,则∠PMO的度数为 .
三、解答题
13.△ABC三个顶点的坐标分别为A(﹣2,1),B(1,2),C(0,3).
(1)请画出△ABC,并画出它向右平移3个单位长度后得到的△A1B1C1;
(2)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并写出点P的坐标.
14.如图,亮亮在A处看护羊群吃草,其家在B处,A,B到河岸的距离分别为AC=200m,BD=100m,CD=400m,亮亮从A处把羊群赶到河边饮水后回家,作图说明亮亮如何行走路程最短,并求出亮亮走的最短路程.
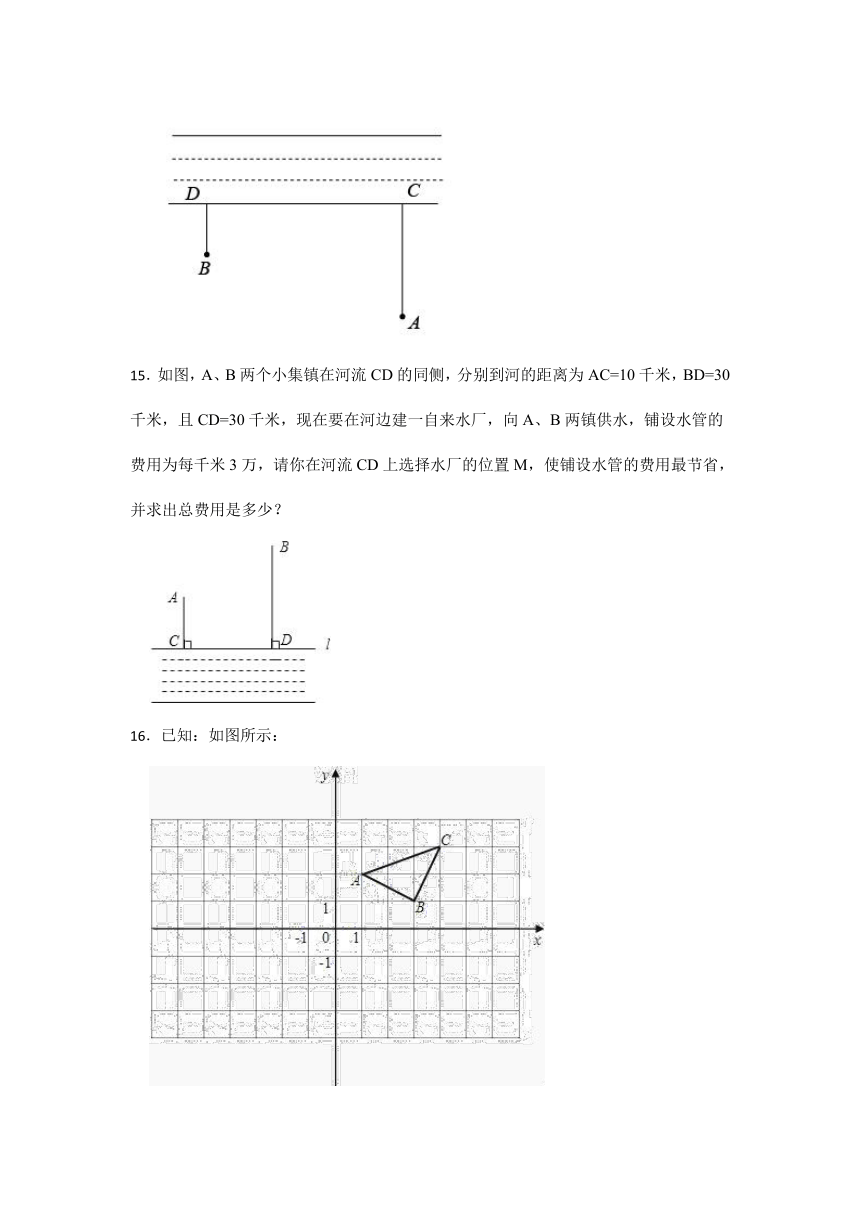
15.如图,A、B两个小集镇在河流CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?
16.已知:如图所示:
作出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′三个顶点的坐标.
17.已知点A(﹣3,﹣4)和B(﹣2,1),试在y轴求一点P,使PA与PB的和最小.
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】D
4.【答案】B
5.【答案】B
6.【答案】D
7.【答案】12
8.【答案】(1)3
(2)-21
9.【答案】2
10.【答案】
11.【答案】
12.【答案】45°
13.【答案】解:(1)如图所示,
(2)作点A关于x轴的对称点A2,连接A2B交x轴与点P,则点P即为所求;
∵A(﹣2,1),
∴A2(﹣2,﹣1),
设直线A2B的解析式为:y=kx+b,
∴,
∴,
∴直线A2B的解析式为:y=x﹣1,
∴P的坐标(﹣1,0).
14.【答案】解:作点B关于河岸的对称点E,连接AE交CD于点P,如图所示:
由轴对称的性质可知:PB=PE,DE=DB,
∴PA+PB=AP+PE,
由两点之间线段最短可知,当点A、P、E在一条直线上时,PA+PB最短,故亮亮的行走路线为A P B时,路程最短;
过点E作EF⊥AC,垂足为F,如图所示,故四边形EDCF为矩形,
∴EF=CD=400m,CF=ED=BD=100m,
最短路程为:
PA+PB=AE
答:亮亮走的最短路程为.
15.【答案】解:作A关于CD的对称点A′,连接A′B与CD,交点CD于M,点M即为所求作的点,
则可得:DK=A′C=AC=10千米,
∴BK=BD+DK=40千米,
∴AM+BM=A′B= =50千米,
总费用为50×3=150万元.
16.【答案】
分别作A、B、C的对称点,A′、B′、C′,由三点的位置可知:
A′(-1,2),B′(-3,1),C′(-4,3)
17.【答案】解:A关于y轴的对称点是C(3,﹣4)则PA=PC,B,C在y轴两侧 则当BPC共线时,PB+PC最小,即PA+PB最小,
设直线BC是y=kx+b,把B,C两点坐标代入:
,
解得:
所以y=﹣x﹣1
y轴上x=0,则y=0﹣1=﹣1,
所以 P(0,﹣1)
一、单选题
1.在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是100°,那么在△ABC中与这100°角对应相等的角是 ( )
A.∠A B.∠B C.∠C D.∠B或∠C
2.如图,点A,B在直线l的同侧,若要用尺规在直线l上确定一点P,使得AP+BP最短,则下列作图正确的是( )
A. B.
C. D.
3.如图,在 中,AB=AC,分别以点A、B为圆心,以适当的长为半径作弧,两弧分别交于E,F,作直线EF,D为BC的中点,M为直线EF上任意一点.若BC=4, 面积为10,则BM+MD长度的最小值为( )
A. B.3 C.4 D.5
4.在△ABC中,已知AB=7,点C到AB的距离为4,则△ABC周长的最小值是( )
A.5+4 B.+7 C.2+ D.以上都不对
5.如图,在平面直角坐标系中,已知A(1,1)、B(3,5),要在y轴上找一点P,使得△PAB的周长最小,则点P的坐标为( )
A.(0,1) B.(0,2) C.( ,0) D.(2,0)
6.如图,在△ 中, , 、 分别是底边 和腰 上的中线,点 为 上一动点,则 的最小值等于( )
A.线段 的长 B.线段 的长
C.线段 的长 D.线段 的长
二、填空题
7.如图,已知∠AOB=45°,∠AOB内有一点P,OP=6 ,M为射线OA上一动点,N为射线OB上一动点,则PM+MN+PN的最小值为 .
8.如图,已知直线 y= x+3 与 x 轴、y 轴分别交于点 A、B,线段 AB 为直角边在第一内作等腰 Rt△ABC,∠BAC=90 . 点 P 是 x 轴上的一个动点,设 P(x,0).
(1)当 x = 时,PB+PC 的值最小;
(2)当 x = 时,|PB-PC|的值最大.
9.如图,等边△ABC中,AB=4,E是线段AC上的任意一点,∠BAC的平分线交BC于D,AD=2 ,F是AD上的动点,连接CF、EF,则CF+EF的最小值为 .
10.如图,在△ABC中,∠ACB=90°,AC=BC=4,D为BC中点,E为AB边上的动点,则△CDE周长的最小值为 .
11.已知△ABC的面积是12,AB=AC=5,AD是BC边上的中线,E,P分别是AC,AD上的动点,则CP+EP的最小值为 .
12.如图,∠AOB=45°,OC平分∠AOB,点M为OB上一定点,P为OC上的一动点,N为OB上一动点,当PM+PN最小时,则∠PMO的度数为 .
三、解答题
13.△ABC三个顶点的坐标分别为A(﹣2,1),B(1,2),C(0,3).
(1)请画出△ABC,并画出它向右平移3个单位长度后得到的△A1B1C1;
(2)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并写出点P的坐标.
14.如图,亮亮在A处看护羊群吃草,其家在B处,A,B到河岸的距离分别为AC=200m,BD=100m,CD=400m,亮亮从A处把羊群赶到河边饮水后回家,作图说明亮亮如何行走路程最短,并求出亮亮走的最短路程.
15.如图,A、B两个小集镇在河流CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?
16.已知:如图所示:
作出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′三个顶点的坐标.
17.已知点A(﹣3,﹣4)和B(﹣2,1),试在y轴求一点P,使PA与PB的和最小.
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】D
4.【答案】B
5.【答案】B
6.【答案】D
7.【答案】12
8.【答案】(1)3
(2)-21
9.【答案】2
10.【答案】
11.【答案】
12.【答案】45°
13.【答案】解:(1)如图所示,
(2)作点A关于x轴的对称点A2,连接A2B交x轴与点P,则点P即为所求;
∵A(﹣2,1),
∴A2(﹣2,﹣1),
设直线A2B的解析式为:y=kx+b,
∴,
∴,
∴直线A2B的解析式为:y=x﹣1,
∴P的坐标(﹣1,0).
14.【答案】解:作点B关于河岸的对称点E,连接AE交CD于点P,如图所示:
由轴对称的性质可知:PB=PE,DE=DB,
∴PA+PB=AP+PE,
由两点之间线段最短可知,当点A、P、E在一条直线上时,PA+PB最短,故亮亮的行走路线为A P B时,路程最短;
过点E作EF⊥AC,垂足为F,如图所示,故四边形EDCF为矩形,
∴EF=CD=400m,CF=ED=BD=100m,
最短路程为:
PA+PB=AE
答:亮亮走的最短路程为.
15.【答案】解:作A关于CD的对称点A′,连接A′B与CD,交点CD于M,点M即为所求作的点,
则可得:DK=A′C=AC=10千米,
∴BK=BD+DK=40千米,
∴AM+BM=A′B= =50千米,
总费用为50×3=150万元.
16.【答案】
分别作A、B、C的对称点,A′、B′、C′,由三点的位置可知:
A′(-1,2),B′(-3,1),C′(-4,3)
17.【答案】解:A关于y轴的对称点是C(3,﹣4)则PA=PC,B,C在y轴两侧 则当BPC共线时,PB+PC最小,即PA+PB最小,
设直线BC是y=kx+b,把B,C两点坐标代入:
,
解得:
所以y=﹣x﹣1
y轴上x=0,则y=0﹣1=﹣1,
所以 P(0,﹣1)
