3.1函数的概念及其表示 课时3 函数的表示法 课件(共29张PPT)
文档属性
| 名称 | 3.1函数的概念及其表示 课时3 函数的表示法 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-04 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
3.1 函数的概念及其表示
课时3 函数的表示法(1)
教学目标
1. 了解表示函数有三种基本方法:解析法、列表法和图象法.理解函数关系的三种表示方法具有内在的联系,在一定的条件下可以互相转化.
2. 能根据问题的具体条件选择恰当的方法表示函数关系,为后面的进一步学习和研究函数的性质奠定基础.
3. 通过实例,感受函数在生产和生活实际中的重要性,体会数和形结合的完美性,提高学生运用数形结合的思想方法分析问题、解决问题的能力.
学习目标
课程目标 学科核心素养
了解函数的三种表示方法,并理解其内在联系 通过对函数的三种表示方法的探索与研究,进一步理解函数的概念,培养数学抽象素养
能选择恰当的方法表示函数关系,构建函数模型 通过构建函数的模型,培养直观想象和数学运算等素养
会运用函数的图象解决有关比较函数值的大小、求函数的值域等问题,体会函数图象的应用 通过运用函数图象解决相关问题,提高数学应用的意识和能力,培养数学运算等素养
情境导学
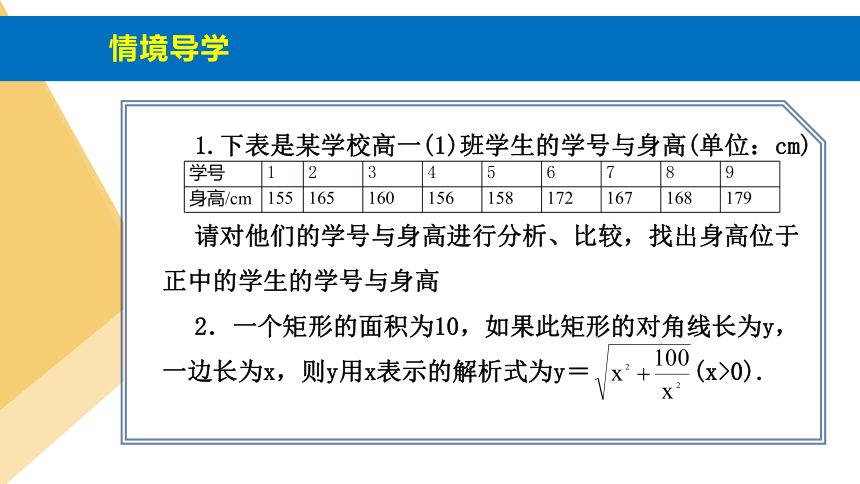
1.下表是某学校高一(1)班学生的学号与身高(单位:cm)
请对他们的学号与身高进行分析、比较,找出身高位于正中的学生的学号与身高
2.一个矩形的面积为10,如果此矩形的对角线长为y,一边长为x,则y用x表示的解析式为y= (x>0).
学号 1 2 3 4 5 6 7 8 9
身高/cm 155 165 160 156 158 172 167 168 179
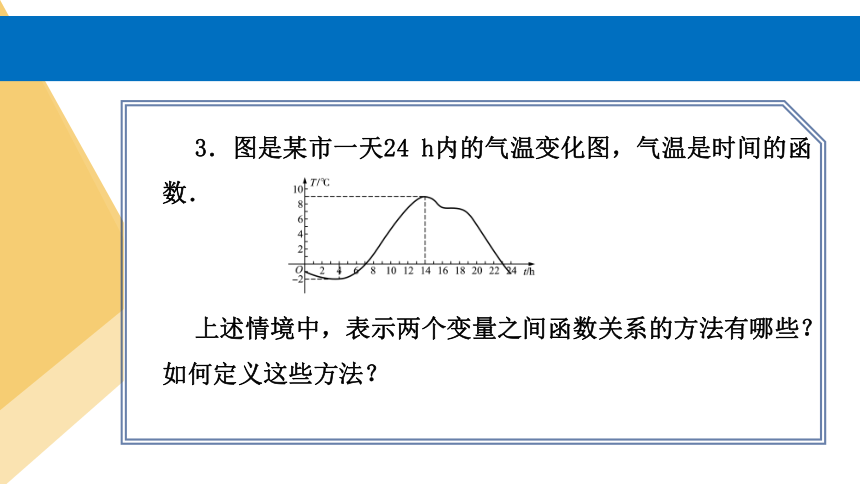
3.图是某市一天24 h内的气温变化图,气温是时间的函数.
上述情境中,表示两个变量之间函数关系的方法有哪些?如何定义这些方法?
【活动1】 比较函数的三种表示法
初探新知
【问题2】试用表格表示问题1中铅笔数x与钱数y之间的关系.
【问题1】某同学计划买x(x∈{1,2,3,4,5})支2B铅笔.每支铅笔的价格为0.5元,共需y元.请你在y与x之间建立一个函数关系.函数的定义域是什么?
【问题4】比较函数的三种表示法,它们各自的特点是什么?说说它们的优缺点.
【问题3】试用图象表示问题1中x与y之间的关系.
【问题5】什么是函数的解析式 试举例说明.
【问题6】怎样求一个函数的值域 谈谈你的想法.
【活动2】求分式函数的值域
【问题7】形如 的函数的值域如何求
【活动3】求根式函数的值域
【问题8】如果函数解析式中含有根式,如
该如何处理?有什么注意点吗?
典例精析
【例1】某商场新进了10台彩电,每台售价3 000元,试分别用列表法、图象法、解析法表示售出台数x(x∈{1,2,3,4,5,6,7,8,9,10})与收款总额y(元)之间的函数关系.
【解】 用列表法表示如下:
x/台 1 2 3 4 5
y/元 3 000 6 000 9 000 12 00 15 000
x/台 6 7 8 9 10
y/元 18 000 21 000 24 000 27 000 30 000
【解】 用图象法表示,如图所示:
用解析法表示为y=3 000x,
x∈{1,2,3,4,5,6,7,8,9,10}.
【方法规律】
函数三种表示法的优缺点:
【变式训练1】某同学到长城旅游,他骑行共享单车由宾馆前往长城,前进了a km,疲惫不堪,休息半小时后,沿原路返回,途中看见路边标语“不到长城非好汉”,便调转车头继续向长城方向前进,则该同学离起点(宾馆)的距离与时间的函数图象大致为( )
C
【解】该同学前进了a km,疲惫不堪,休息半小时后,此时到宾馆的距离不变为常数,排除A;沿原路返回的过程,随时间的增加路程减少,排除B,D;途中看见路边标语“不到长城非好汉”,便调转车头继续向长城方向前进,此时到宾馆的距离随时间的增加逐步增加.故选C.
【例2】画出函数f(x)=-x2+2x+3的图象,并根据图象解答下列问题:
(1) 比较f(0),f(1),f(3)的大小;
(2) 若x1(3) 求函数f(x)的值域.
思路点拨:识图→识图→分析→下结论.
【解】令函数y=f(x)=-x2+2x+3,其定义域为R,列表:
描点,连线,得函数图象如图所示:
(1) 根据图象,容易发现f(0)=3,
f(1)=4,f(3)=0,所以f(3)(2) 根据图象,容易发现
当x1(3) 可以看出函数的图象是以(1,4)为顶点、开口向下的抛物线,因此,函数的值域为(-∞,4].
x … -2 -1 0 1 2 3 4 …
y … -5 0 3 4 3 0 -5 …
【方法规律】
函数图象形象、直观地反映了函数的对称性、函数的值域及函数值随自变量变化而变化的趋势.
【变式训练2】 [2020·枣庄市联考]如图,函数f(x)的图象是曲线OAB,则f( )的值等于________.
【解】 由图象知f(3)=1,故f( )=f(1)=2.
2
思路点拨 根据函数的结构特点,选择求函数值域的方法.
【解】
【例3】求下列函数的值域:
(1)
(2)
【方法规律】
换元法、分离变量法是求解函数值域的有效方法,但要注意各方法所适用的函数形式,还要注意函数定义域的限制.换元法多用于无理函数,换元的目的是进行化归,把无理式转化为有理式来求解;分式型函数求值域,多采用分离变量法,分离出整式来处理.
【变式训练3】
【解】
思路点拨:(1) 根据解析式将自变量代入解析式即可求解. (2) 由解析式将代入解析式,整理化简即可证出. (3) 由(2)即可求解.
(备选例题)
【解】
【方法规律】
函数解析式是表示两个变量间的函数关系的一种重要的方法,有了解析式,能够很方便地求出函数的值,有时还可以根据解析式画出函数图象,求出函数的值域等.
课堂反思
通过本节课的学习,你学到了什么?
2.你认为本节课的重点和难点是什么?
随堂演练
1.[2022·上海市高考二模改编题]若函数y=f(x)的值域为[-1,1],则函数y=f(x+2)的值域为 ( )
A. [-1,1] B. [-1,0]
C. [0,1] D. [2,8]
A
2.函数f(x)=x- 的值域为( )
A. B.
C. D.
3. (多选)下列四个命题中,错误的是( )
A. f(x)= + 是函数
B. 函数的定义域或值域可以是空集
C. 函数y=x2+2x+3(x∈N)的图象是一条抛物线
D. 若函数y= 的定义域为R,则0≤a≤1
A
ABC
5.已知f(x)的图象如图所示,则f(x)的定义域为 ________,值域为________.
4. 函数f(x)= 的值域为________.
(1,2]
[-4,3]
[-2,4]U[5,8]
同学们再见!
Goodbye Students!
3.1 函数的概念及其表示
课时3 函数的表示法(1)
教学目标
1. 了解表示函数有三种基本方法:解析法、列表法和图象法.理解函数关系的三种表示方法具有内在的联系,在一定的条件下可以互相转化.
2. 能根据问题的具体条件选择恰当的方法表示函数关系,为后面的进一步学习和研究函数的性质奠定基础.
3. 通过实例,感受函数在生产和生活实际中的重要性,体会数和形结合的完美性,提高学生运用数形结合的思想方法分析问题、解决问题的能力.
学习目标
课程目标 学科核心素养
了解函数的三种表示方法,并理解其内在联系 通过对函数的三种表示方法的探索与研究,进一步理解函数的概念,培养数学抽象素养
能选择恰当的方法表示函数关系,构建函数模型 通过构建函数的模型,培养直观想象和数学运算等素养
会运用函数的图象解决有关比较函数值的大小、求函数的值域等问题,体会函数图象的应用 通过运用函数图象解决相关问题,提高数学应用的意识和能力,培养数学运算等素养
情境导学
1.下表是某学校高一(1)班学生的学号与身高(单位:cm)
请对他们的学号与身高进行分析、比较,找出身高位于正中的学生的学号与身高
2.一个矩形的面积为10,如果此矩形的对角线长为y,一边长为x,则y用x表示的解析式为y= (x>0).
学号 1 2 3 4 5 6 7 8 9
身高/cm 155 165 160 156 158 172 167 168 179
3.图是某市一天24 h内的气温变化图,气温是时间的函数.
上述情境中,表示两个变量之间函数关系的方法有哪些?如何定义这些方法?
【活动1】 比较函数的三种表示法
初探新知
【问题2】试用表格表示问题1中铅笔数x与钱数y之间的关系.
【问题1】某同学计划买x(x∈{1,2,3,4,5})支2B铅笔.每支铅笔的价格为0.5元,共需y元.请你在y与x之间建立一个函数关系.函数的定义域是什么?
【问题4】比较函数的三种表示法,它们各自的特点是什么?说说它们的优缺点.
【问题3】试用图象表示问题1中x与y之间的关系.
【问题5】什么是函数的解析式 试举例说明.
【问题6】怎样求一个函数的值域 谈谈你的想法.
【活动2】求分式函数的值域
【问题7】形如 的函数的值域如何求
【活动3】求根式函数的值域
【问题8】如果函数解析式中含有根式,如
该如何处理?有什么注意点吗?
典例精析
【例1】某商场新进了10台彩电,每台售价3 000元,试分别用列表法、图象法、解析法表示售出台数x(x∈{1,2,3,4,5,6,7,8,9,10})与收款总额y(元)之间的函数关系.
【解】 用列表法表示如下:
x/台 1 2 3 4 5
y/元 3 000 6 000 9 000 12 00 15 000
x/台 6 7 8 9 10
y/元 18 000 21 000 24 000 27 000 30 000
【解】 用图象法表示,如图所示:
用解析法表示为y=3 000x,
x∈{1,2,3,4,5,6,7,8,9,10}.
【方法规律】
函数三种表示法的优缺点:
【变式训练1】某同学到长城旅游,他骑行共享单车由宾馆前往长城,前进了a km,疲惫不堪,休息半小时后,沿原路返回,途中看见路边标语“不到长城非好汉”,便调转车头继续向长城方向前进,则该同学离起点(宾馆)的距离与时间的函数图象大致为( )
C
【解】该同学前进了a km,疲惫不堪,休息半小时后,此时到宾馆的距离不变为常数,排除A;沿原路返回的过程,随时间的增加路程减少,排除B,D;途中看见路边标语“不到长城非好汉”,便调转车头继续向长城方向前进,此时到宾馆的距离随时间的增加逐步增加.故选C.
【例2】画出函数f(x)=-x2+2x+3的图象,并根据图象解答下列问题:
(1) 比较f(0),f(1),f(3)的大小;
(2) 若x1
思路点拨:识图→识图→分析→下结论.
【解】令函数y=f(x)=-x2+2x+3,其定义域为R,列表:
描点,连线,得函数图象如图所示:
(1) 根据图象,容易发现f(0)=3,
f(1)=4,f(3)=0,所以f(3)
当x1
x … -2 -1 0 1 2 3 4 …
y … -5 0 3 4 3 0 -5 …
【方法规律】
函数图象形象、直观地反映了函数的对称性、函数的值域及函数值随自变量变化而变化的趋势.
【变式训练2】 [2020·枣庄市联考]如图,函数f(x)的图象是曲线OAB,则f( )的值等于________.
【解】 由图象知f(3)=1,故f( )=f(1)=2.
2
思路点拨 根据函数的结构特点,选择求函数值域的方法.
【解】
【例3】求下列函数的值域:
(1)
(2)
【方法规律】
换元法、分离变量法是求解函数值域的有效方法,但要注意各方法所适用的函数形式,还要注意函数定义域的限制.换元法多用于无理函数,换元的目的是进行化归,把无理式转化为有理式来求解;分式型函数求值域,多采用分离变量法,分离出整式来处理.
【变式训练3】
【解】
思路点拨:(1) 根据解析式将自变量代入解析式即可求解. (2) 由解析式将代入解析式,整理化简即可证出. (3) 由(2)即可求解.
(备选例题)
【解】
【方法规律】
函数解析式是表示两个变量间的函数关系的一种重要的方法,有了解析式,能够很方便地求出函数的值,有时还可以根据解析式画出函数图象,求出函数的值域等.
课堂反思
通过本节课的学习,你学到了什么?
2.你认为本节课的重点和难点是什么?
随堂演练
1.[2022·上海市高考二模改编题]若函数y=f(x)的值域为[-1,1],则函数y=f(x+2)的值域为 ( )
A. [-1,1] B. [-1,0]
C. [0,1] D. [2,8]
A
2.函数f(x)=x- 的值域为( )
A. B.
C. D.
3. (多选)下列四个命题中,错误的是( )
A. f(x)= + 是函数
B. 函数的定义域或值域可以是空集
C. 函数y=x2+2x+3(x∈N)的图象是一条抛物线
D. 若函数y= 的定义域为R,则0≤a≤1
A
ABC
5.已知f(x)的图象如图所示,则f(x)的定义域为 ________,值域为________.
4. 函数f(x)= 的值域为________.
(1,2]
[-4,3]
[-2,4]U[5,8]
同学们再见!
Goodbye Students!
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
