人教版高中数学必修第一册3.1函数的概念及其表示 课时4 函数的表示法(2) 课件(共25张PPT)
文档属性
| 名称 | 人教版高中数学必修第一册3.1函数的概念及其表示 课时4 函数的表示法(2) 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 792.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-04 20:44:52 | ||
图片预览







文档简介
(共25张PPT)
3.1 函数的概念及其表示
课时4 函数的表示法(2)
高考导向
1. 通过具体实例,了解分段函数的概念及其表示方法,掌握其简单应用.
2. 通过具体问题,掌握求函数解析式的几种常见方法,理解其适用范围.
3. 能够求解有关函数解析式的综合性问题,提高分析和解决问题的能力.
学习目标
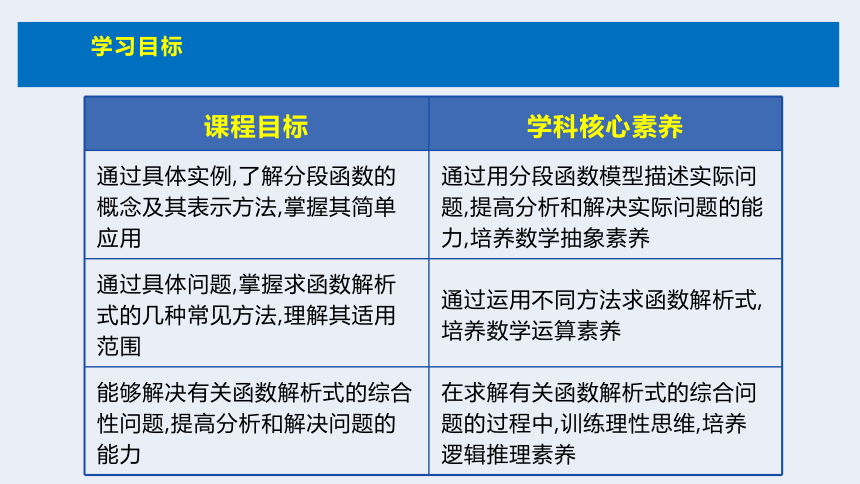
课程目标 学科核心素养
通过具体实例,了解分段函数的概念及其表示方法,掌握其简单应用 通过用分段函数模型描述实际问题,提高分析和解决实际问题的能力,培养数学抽象素养
通过具体问题,掌握求函数解析式的几种常见方法,理解其适用范围 通过运用不同方法求函数解析式,培养数学运算素养
能够解决有关函数解析式的综合性问题,提高分析和解决问题的能力 在求解有关函数解析式的综合问题的过程中,训练理性思维,培养逻辑推理素养
情境导学
人们常说,数学来源于生活,生活赋予数学美感,数学离开生活就会枯燥无味.
国内投寄信函(本埠),假设每封信函不超过20 g时付邮资0.8元,超过20 g不超过40 g时付邮资1.6元,以此类推,每封x(0【活动1】 理解分段函数的概念
初探新知
【问题2】上述x与y之间的关系有何特点?
【问题1】情境导学中的x与y是否具有函数关系?若有,其定义域、值域各是什么?
【问题3】你知道这类函数的名称吗?它的定义是什么?它是一个函数,还是几个函数?
【问题4】这类函数的定义域和值域如何求?它的图象有什么特点?
【问题5】已知f(x+1)=x2-3x+2,求f(x)的解析式.
【活动2】探究求函数解析式的常见方法
【问题6】已知f(x2+1)=3x4+2x2-1,求f(x).
【问题7】已知2f(x)+f( )=3x,请你采用适当方法求出f(x)的解析式.
【问题8】已知f(x)为一次函数,且f(1)=0,f(3)=2,请你采用适当方法求出f(x)的解析式.
【问题9】上述求函数解析式的几种方法各自的特点是什么?
【活动3】理解求函数解析式的几种方法的特点
【问题10】在上述的几种方法中,待定系数法相对简单,可以适用于所有情况吗?
典例精析
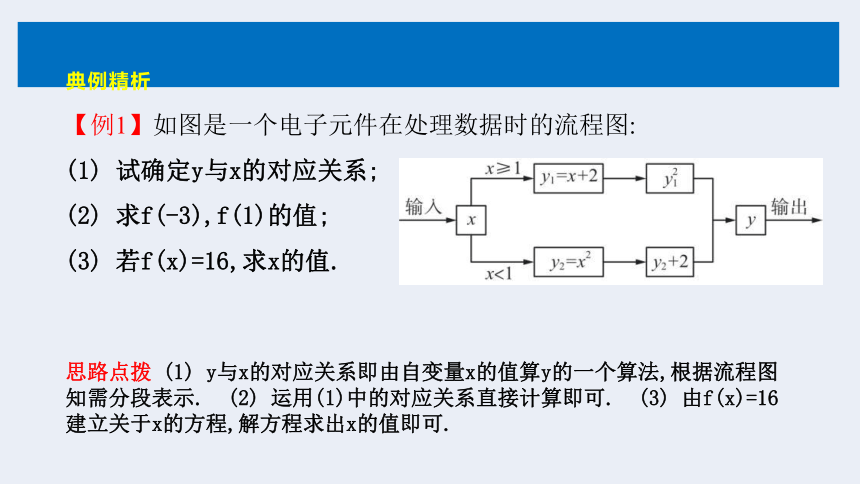
思路点拨 (1) y与x的对应关系即由自变量x的值算y的一个算法,根据流程图知需分段表示. (2) 运用(1)中的对应关系直接计算即可. (3) 由f(x)=16建立关于x的方程,解方程求出x的值即可.
【例1】如图是一个电子元件在处理数据时的流程图:
(1) 试确定y与x的对应关系;
(2) 求f(-3),f(1)的值;
(3) 若f(x)=16,求x的值.
【方法规律】:在不同的定义区间上有不同的对应关系的函数叫做分段函数.分段函数的求值问题的解题思路:① 求函数值:当出现f(f(a))的形式时,应从内到外依次求值.② 求自变量的值:先假设所求的值在分段函数定义区间的各段上,然后求出相应自变量的值,切记要代入检验.
【解】
【变式训练1】
【解】
【例2】[教材改编题]已知f(x+1)=x2-3x+2,求f(x).
思路点拨 思路一:令x+1=t,换元求解.思路二:采用配凑法,将等式右边配凑成关于(x+1)的式子.
【解】
【方法规律】
我们把没有给出具体解析式的函数称为抽象函数.在抽象函数问题中,当不知道函数类型时,一般可采用换元法或配凑法求函数解析式.使用换元法或配凑法时要注意自变量取值范围的变化情况.
【变式训练2】 已知f( +1)=x+2 ,求f(x)的解析式.
【解】方法1(配凑法):f( +1)=( )2+2 +1-1=
( +1)2-1,其中 +1≥1.故所求函数的解析式为f(x)=x2-1,其中x≥1.
方法2(换元法):令 +1=t,则x=(t-1)2,且t≥1,则函数f( +1)=x+2 可化为f(t)=(t-1)2+2(t-1)=t2-1,故所求函数的解析式为f(x)=x2-1,其中x≥1.
【例3】已知f(x)是二次函数,且满足f(0)=1,f(x+1)-f(x)=2x,求f(x)的解析式.
思路点拨 运用待定系数法求解.
【解】
【方法规律】
在抽象函数问题中,已知函数解析式的类型及函数的某些特征,可设出其函数解析式,利用待定系数法求解,这里包含着方程思想的应用.待定系数法一般用于函数是多项式的情况.
【变式训练3】已知f(x)是一次函数,且f(f(x))=2x-1,求f(x)的解析式.
【解】
(备选例题)[教材改编题]已知函数f(x)对于任意的x有f(x)+2f(-x)=3x-2,求f(x).
思路点拨 将x替换为-x,得到第二个恒等式,与第一个恒等式构成方程组求解.
【解】
【方法规律】
如果在已知式子中含有关于两个不同变量的函数,而这两个变量有着某种关系,这时就可以依据两个变量的关系,建立一个新的关于这两个变量的式子,由这两个式子建立方程组,通过解方程组消去一个变量,从而得到目标变量的解析式.这种方法叫做构造方程组法.构造方程组法也是求函数解析式的重要方法之一.
课堂反思
通过本节课的学习,你学到了什么?
2.你认为本节课的重点和难点是什么?
随堂演练
1.
B
2.[教材改编题]已知函数f(x)= 则函数f(x)的图象是( )
A
BC
5.已知函数F(x)=f(x)+g(x),其中f(x)是x的正比例函数,g(x)是x的反比例函数,且F( )=16,F(1)=8,则F(x)的解析式为________________.
4. 若函数f(x)满足f(3x+2)=9x+8,则f(x)=________.
3x+2
同学们再见!
Goodbye Students!
3.1 函数的概念及其表示
课时4 函数的表示法(2)
高考导向
1. 通过具体实例,了解分段函数的概念及其表示方法,掌握其简单应用.
2. 通过具体问题,掌握求函数解析式的几种常见方法,理解其适用范围.
3. 能够求解有关函数解析式的综合性问题,提高分析和解决问题的能力.
学习目标
课程目标 学科核心素养
通过具体实例,了解分段函数的概念及其表示方法,掌握其简单应用 通过用分段函数模型描述实际问题,提高分析和解决实际问题的能力,培养数学抽象素养
通过具体问题,掌握求函数解析式的几种常见方法,理解其适用范围 通过运用不同方法求函数解析式,培养数学运算素养
能够解决有关函数解析式的综合性问题,提高分析和解决问题的能力 在求解有关函数解析式的综合问题的过程中,训练理性思维,培养逻辑推理素养
情境导学
人们常说,数学来源于生活,生活赋予数学美感,数学离开生活就会枯燥无味.
国内投寄信函(本埠),假设每封信函不超过20 g时付邮资0.8元,超过20 g不超过40 g时付邮资1.6元,以此类推,每封x(0
初探新知
【问题2】上述x与y之间的关系有何特点?
【问题1】情境导学中的x与y是否具有函数关系?若有,其定义域、值域各是什么?
【问题3】你知道这类函数的名称吗?它的定义是什么?它是一个函数,还是几个函数?
【问题4】这类函数的定义域和值域如何求?它的图象有什么特点?
【问题5】已知f(x+1)=x2-3x+2,求f(x)的解析式.
【活动2】探究求函数解析式的常见方法
【问题6】已知f(x2+1)=3x4+2x2-1,求f(x).
【问题7】已知2f(x)+f( )=3x,请你采用适当方法求出f(x)的解析式.
【问题8】已知f(x)为一次函数,且f(1)=0,f(3)=2,请你采用适当方法求出f(x)的解析式.
【问题9】上述求函数解析式的几种方法各自的特点是什么?
【活动3】理解求函数解析式的几种方法的特点
【问题10】在上述的几种方法中,待定系数法相对简单,可以适用于所有情况吗?
典例精析
思路点拨 (1) y与x的对应关系即由自变量x的值算y的一个算法,根据流程图知需分段表示. (2) 运用(1)中的对应关系直接计算即可. (3) 由f(x)=16建立关于x的方程,解方程求出x的值即可.
【例1】如图是一个电子元件在处理数据时的流程图:
(1) 试确定y与x的对应关系;
(2) 求f(-3),f(1)的值;
(3) 若f(x)=16,求x的值.
【方法规律】:在不同的定义区间上有不同的对应关系的函数叫做分段函数.分段函数的求值问题的解题思路:① 求函数值:当出现f(f(a))的形式时,应从内到外依次求值.② 求自变量的值:先假设所求的值在分段函数定义区间的各段上,然后求出相应自变量的值,切记要代入检验.
【解】
【变式训练1】
【解】
【例2】[教材改编题]已知f(x+1)=x2-3x+2,求f(x).
思路点拨 思路一:令x+1=t,换元求解.思路二:采用配凑法,将等式右边配凑成关于(x+1)的式子.
【解】
【方法规律】
我们把没有给出具体解析式的函数称为抽象函数.在抽象函数问题中,当不知道函数类型时,一般可采用换元法或配凑法求函数解析式.使用换元法或配凑法时要注意自变量取值范围的变化情况.
【变式训练2】 已知f( +1)=x+2 ,求f(x)的解析式.
【解】方法1(配凑法):f( +1)=( )2+2 +1-1=
( +1)2-1,其中 +1≥1.故所求函数的解析式为f(x)=x2-1,其中x≥1.
方法2(换元法):令 +1=t,则x=(t-1)2,且t≥1,则函数f( +1)=x+2 可化为f(t)=(t-1)2+2(t-1)=t2-1,故所求函数的解析式为f(x)=x2-1,其中x≥1.
【例3】已知f(x)是二次函数,且满足f(0)=1,f(x+1)-f(x)=2x,求f(x)的解析式.
思路点拨 运用待定系数法求解.
【解】
【方法规律】
在抽象函数问题中,已知函数解析式的类型及函数的某些特征,可设出其函数解析式,利用待定系数法求解,这里包含着方程思想的应用.待定系数法一般用于函数是多项式的情况.
【变式训练3】已知f(x)是一次函数,且f(f(x))=2x-1,求f(x)的解析式.
【解】
(备选例题)[教材改编题]已知函数f(x)对于任意的x有f(x)+2f(-x)=3x-2,求f(x).
思路点拨 将x替换为-x,得到第二个恒等式,与第一个恒等式构成方程组求解.
【解】
【方法规律】
如果在已知式子中含有关于两个不同变量的函数,而这两个变量有着某种关系,这时就可以依据两个变量的关系,建立一个新的关于这两个变量的式子,由这两个式子建立方程组,通过解方程组消去一个变量,从而得到目标变量的解析式.这种方法叫做构造方程组法.构造方程组法也是求函数解析式的重要方法之一.
课堂反思
通过本节课的学习,你学到了什么?
2.你认为本节课的重点和难点是什么?
随堂演练
1.
B
2.[教材改编题]已知函数f(x)= 则函数f(x)的图象是( )
A
BC
5.已知函数F(x)=f(x)+g(x),其中f(x)是x的正比例函数,g(x)是x的反比例函数,且F( )=16,F(1)=8,则F(x)的解析式为________________.
4. 若函数f(x)满足f(3x+2)=9x+8,则f(x)=________.
3x+2
同学们再见!
Goodbye Students!
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
