21.3 实际问题与一元二次方程同步练习题(含解析)
文档属性
| 名称 | 21.3 实际问题与一元二次方程同步练习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 807.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-04 22:38:53 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
人教版九年级数学上册
21.3 实际问题与一元二次方程 同步练习题
一、单选题
1.有一人患了流感,经过两轮传染后,共有人患了流感,每轮传染中平均每人传染了( )个人
A.11 B.12 C.13 D.14
2.海南省某企业年月份利润为万元,要使月份的利润为万元,则每月的平均增长率是( )
A. B. C. D.
3.某小区花园有一块长方形花圃,它的宽为,若长边不变,将短边扩大,使得扩大后的花圃形状为正方形,且面积比原来增加,设原来花圃长边为,可列方程( )
A. B.
C. D.
4.如图,这是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点…,第行有个点…,前行的点数和不能是以下哪个结果( )
A.45 B.66 C.100 D.210
5.某商店经销一种销售成本为40元的水果,据市场分析,若按每千克50元销售,一个月能售出500千克:销售单价每涨1元,月销售量就减少10千克,设销售单价为每千克()元,月销售利润达8000元.则方程为( )
A. B.
C. D.
6.在中,,动点P从点A沿线段向点B移动,一动点Q从点B沿线段向点C移动,两点同时开始移动,点的速度为,点的速度为,当到达点时两点同时停止运动.若使的面积为,则点P运动的时间是( )
A.1s B.4s C.5s或1s D.4s或1s
7.一辆汽车以20m/s的速度行驶,司机发现前方路面26m处有情况,紧急刹车后汽车又滑行25m后停车,问刹车后汽车滑行到16m时约用了( )
A.1s B.1.2s C.2s D.4s
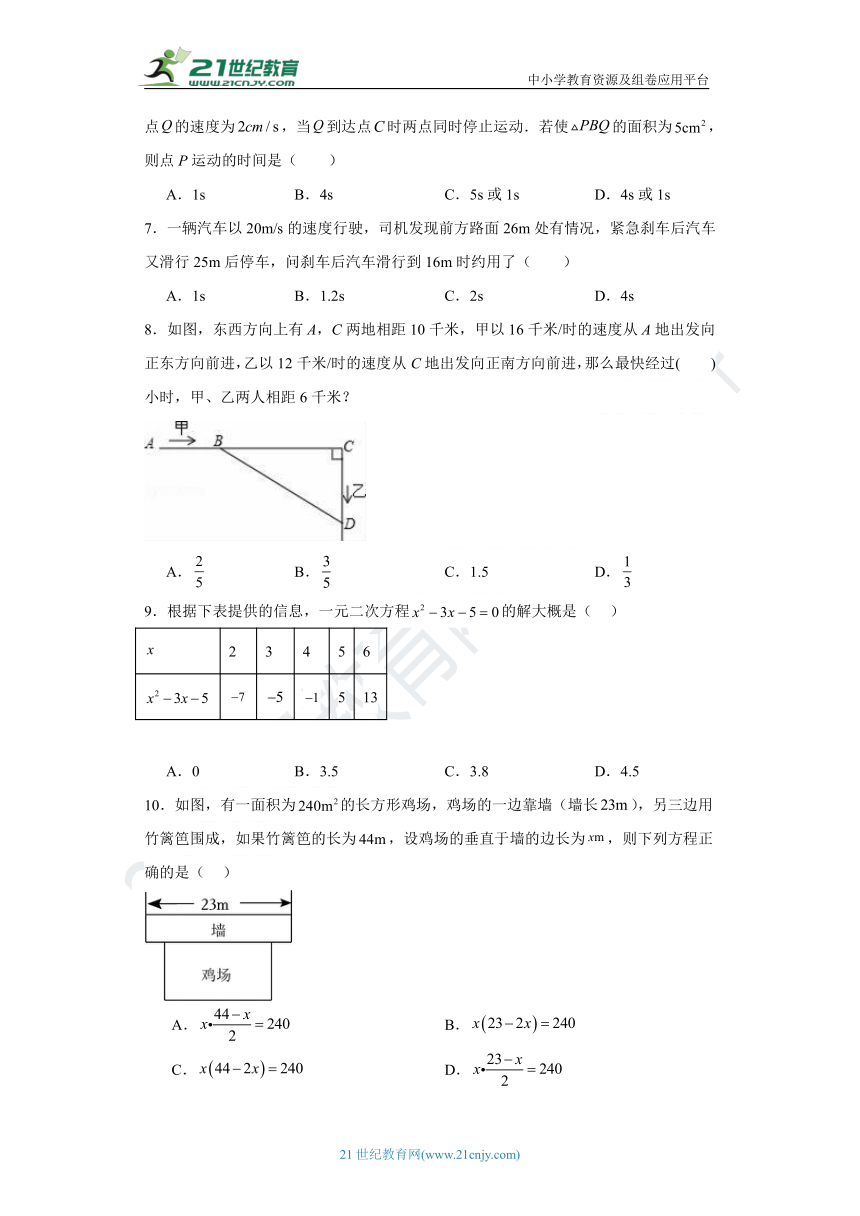
8.如图,东西方向上有A,C两地相距10千米,甲以16千米/时的速度从A地出发向正东方向前进,乙以12千米/时的速度从C地出发向正南方向前进,那么最快经过( )小时,甲、乙两人相距6千米?
A. B. C.1.5 D.
9.根据下表提供的信息,一元二次方程的解大概是( )
2 3 4 5 6
5 13
A.0 B.3.5 C.3.8 D.4.5
10.如图,有一面积为的长方形鸡场,鸡场的一边靠墙(墙长),另三边用竹篱笆围成,如果竹篱笆的长为,设鸡场的垂直于墙的边长为,则下列方程正确的是( )
A. B.
C. D.
二、填空题
11.某学校组织篮球比赛,实行单循环制,共有36场比赛,则参加的队数为 .
12.如图,要设计一幅宽20cm,长30cm的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为,如果要使所有彩条所占面积为原矩形图案面积的三分之一,竖彩条的宽度是 cm.
13.2023“全晋乐购”网上年货节活动期间,某商家购进一批进价为80元/盒的吕梁沙棘汁,按150元/盒的价格进行销售,每天可售出160盒.后经市场调查发现,当每盒价格降低1元时,每天可多售出8盒.若要每天盈利16000元,设每盒价格降低元,则可列方程为 .
14.一个小球以速度开始向前滚动,并且均匀减速,后小球停止滚动.小球滚动约用了 秒(结果保留小数点后一位)
15.一个小组若干人,新年每人互送贺卡一张,已知全组共送贺卡30张,则这个小组有 人.
三、解答题
16.圣诞节昂立师生互送贺卡,总共送出张,求昂立共有师生多少人?
17.随着国家“惠民政策”的陆续出台,为了切实让老百姓得到实惠,国家卫计委通过严打药品销售环节中的不正当行为,以维护老百姓的利益.某种药品原价600元/瓶,经过连续两次降价后,现在仅卖384元/瓶.求该种药品平均每次降价的百分率.
18.将一个正方形的场地扩建,一边加长,一边加长后变成矩形,且矩形的面积是,求原来正方形的边长.
19.一个两位数是一个一位数的平方,把这个一位数放在这个两位数的左边所成的三位数,比把这个一位数放在这个两位数的右边所成的三位数大,求这个两位数.
20.在“五一”期间,某水果超市调查两种新疆干枣的销售情况,下面是调查员的对话:
小王:干枣的进价是每千克8元,售价16元,干枣的进价是每千克14元,售价20元.
小张:当干枣销售价每千克20元时,每天可售出30千克,若每千克降低1元,平均每天可多售出10千克.
根据他们的对话,解决下面所给的问题:
(1)该水果店第一次用2500元直接购进这两种干枣共200千克,问这两种干枣各购进多少千克?若全部售出,共获得多少利润?
(2)为了给顾客优惠,将销售价定为每千克多少元时,才能使干枣平均每天的销售利润为200元?
21.已知,一辆汽车在笔直的公路上刹车后,该车的速度米秒与时间秒之间满足一次函数关系,其图象如图所示;
(1)求与之间的函数关系式;
(2)已知汽车在该运动状态下,一段时间内向前滑行的距离等于这段时间内的平均速度乘以时间该运动状态下的平均速度,表示这段时间起始时刻的速度,表示这段时间结束时刻的速度.若该车刹车后秒内向前滑行了米,求的值.
22.如图,矩形中,,,点从开始沿边向点以厘米/秒的速度移动,点从点开始沿边向点以厘米/秒的速度移动,如果、分别是从同时出发,求经过几秒时,
(1)的面积等于平方厘米?
(2)五边形的面积最小?最小值是多少?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【分析】患流感的人把病毒传染给别人,自己仍然患病,包括在总数中.设每轮传染中平均一个人传染了x个人,则第一轮传染了x个人,第二轮作为传染源的是人,则传染人,依题意列方程:,解方程即可求解.
【详解】设每轮传染中平均一个人传染了x个人,依题意得
,即,
解方程得(舍去),
即每轮传染中平均每人传染了个人,
故选:B
【点睛】此题考查了一元二次方程的应用,解题的关键是读懂题目,从实际问题中抽象出方程模型,设出未知数,找出等量关系,列方程.
2.C
【分析】设每月的平均增长率是,由题意:月份利润为万元,要使月份的利润为万元,列出一元二次方程,解方程即可.
【详解】解:设每月的平均增长率是,
由题意得:,
解得:,不符合题意,舍去.
即每月的平均增长率是,
故选:C.
【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
3.B
【分析】设原来花圃长边为,则短边增加了,再根据面积增加了列出方程即可.
【详解】解:,设原来花圃长边为,则短边增加了,
由题意得,,即,
故选B.
【点睛】本题主要考查了从实际问题中抽象出一元二次方程,正确理解题意找到等量关系是解题的关键.
4.C
【分析】由于第一行有1个点,第二行有2个点…第n行有n个点…,则前n行共有个点,然后根据选项分别求出n的值,即可作出判断.
【详解】通过观察图形可知:第一行有1个点,第二行有2个点…第n行有n个点,
前n行共有个点,其中n为正整数.
∴当时,解得:(舍去),;
当时,解得:(舍去), ;
当时,解得:(舍去),(舍去),即前行的点数和不能是100;
当时,解得:(舍去),.
故选:C.
【点睛】本题主要考查的是探究图形的规律,一元二次方程的解.正确得到前行的点数和的式子是解题的关键.
5.A
【分析】根据题意销售单价每涨1元,月销售量就减少10千克,得到销售单价为时销量为:,再根据:利润(单价成本)数量,列出方程即可得出答案.
【详解】解:售价为时的销量为:,
月销售利润达8000时得:,
故答案选:A.
【点睛】本题考查了一元二次方程的应用,理解题意找出数量关系列出方程是解题关键.
6.A
【分析】设点运动的时间为,则,,利用三角形的面积计算公式,即可得出关于的一元二次方程,解之即可得出的值,再结合当到达点时两点同时停止运动,即可得出点运动的时间.
【详解】解:设点运动的时间为,则,,
依题意得:,
整理得:,
解得:,,
当到达点时两点同时停止运动,
,
,
.
故选:A.
【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
7.A
【分析】等量关系为:平均速度×时间=16,把相关数值代入即可求解.
【详解】解:设约用了x秒.
汽车每秒减少的速度为:20÷[25÷(20÷2)]=8,
∴16米时的平均速度为:[20+(20﹣8x)]÷2=20﹣4x.
∴(20﹣4x)×x=16,
解得:x1=1,x2=4,
∵20﹣8x>0,
∴x=1,
故选:A.
【点睛】本题考查了一元二次方程的应用,用到的知识点为:匀变速运动的物体的平均速度=初速度与末速度和的一半;每秒减少的速度等于初速度与末速度之差与所用时间的比值.
8.A
【分析】根据题意表示出BC,DC的长,进而利用勾股定理求出答案
【详解】解:设最快经过x小时,甲、乙两人相距6km,根据题意可得:
BC=(10﹣16x)km,DC=12xkm,
因为BC2+DC2=BD2,
则(10﹣16x)2+(12x)2=62,
解得:x1=x2=0.4.
答:最快经过0.4小时,甲、乙两人相距6km.
故选A.
【点睛】此题主要考查了勾股定理以及一元二次方程的应用,利用勾股定理列出方程是解题的关键.
9.D
【分析】根据表格数据,找出代数式从变为时的取值范围即可判断
【详解】时,,
时,,
则的解的范围为,
即一元二次方程的解大概是4.5.
故选D.
【点睛】本题考查了估算一元二次方程的解的近似值,根据表格获得信息是解题的关键.
10.C
【分析】已知长方形鸡场垂直于墙的边长(即长方形鸡场的宽)为,结合竹篱笆的长度,可求得长方形鸡场的长,根据面积的等量关系,可列出方程.
【详解】解:设鸡场的垂直于墙的边长为,鸡场平行于墙的边长为:,
根据面积的等量关系,得:
.
故选:C.
【点睛】本题主要考查列二元一次方程,根据题意找到等量关系并用未知数表示出来是解题的关键.
11.9
【分析】设有个球队参加比赛,那么第一个队和其他队打场球,第二个队和其他队打场,以此类推可以知道共打场,然后列出方程求解.
【详解】解:设邀请个球队参加比赛,
依题意得,
即,
,
或(不合题意,舍去).
故答案为:9.
【点睛】此题考查了一元二次方程的应用,该题和实际生活结合比较紧密,准确找到关键描述语,从而根据等量关系准确地列出方程是解决问题的关键.此题还要判断所求的解是否符合题意,舍去不合题意的解.
12.
【分析】设横彩条的宽度为,则竖彩条的宽度为,则由图可知一个横彩条的面积为,一个竖彩条的面积为,重叠的面积为,接下来根据所有彩条所占面积为原矩形图案面积的三分之一可得,解方程,问题便可解答.
【详解】解:设横彩条的宽度为,则竖彩条的宽度为,则
,
解得,(舍去),
∴,
∴竖的彩条宽为.
故答案为:.
【点睛】本题属于一元二次方程的应用,找出等量关系是解答本题的关键.
13.
【分析】设每件商品售价降低元,根据“每天盈利16000元”列出一元二次方程即可.
【详解】解:设每件商品售价降低元,平均每天可售出盒.
依题意得:,
故答案为:.
【点睛】本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
14.1.2.
【分析】利用等量关系:速度时间=路程,时间为,根据题意列出方程:求解即可.
【详解】由题意得:小球的平均滚动速度是,
设小球滚动5时约用了,
由题意得:,
整理得:,
解得:,
∵,
∴,
故小球滚动用了1.2秒.
【点睛】本题考查了一元二次方程的应用,重点在于求出平均每秒小球的运动减少的速度,读懂题意是解题的关键.
15.6
【分析】设这个小组有x个人,则每个人送出张贺卡,再根据全组共送贺卡30张建立方程求解即可.
【详解】解:设这个小组有x个人,
由题意得:
解得(舍去),
∴这个小组有6人
故答案为:6.
【点睛】本题主要考查了一元二次方程的事件应用,根据每个人送出张贺卡建立方程是解题的关键.
16.31人
【分析】设昂立共有师生人,再建立方程:,再解方程即可.
【详解】解:设昂立共有师生人,
由题意可得:,
整理得:,解得:,(负值舍去).
答:昂立共有师生31人.
【点睛】本题主要考查互送卡片问题,一元二次方程的应用,确定相等关系是解本题的关键,注意由于每人都要送到,因此不用除2.
17.20%
【分析】设该种药品平均每次降价的百分率为x,则第一次降价后的单价是原来的,第二次降价后的单价是原来的,根据题意列方程解答即可.
【详解】解:设该种药品平均每次降价的百分率为,
由题意得:,
解得:,(不合题意舍去),
∴,
答:该种药品平均每次降价的百分率为20%.
【点睛】此题主要考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
18.
【分析】先原来的正方形的边长为,则一边长为:,另一边长为:,根据题意列出方程,解方程即可.
【详解】解:设原来的正方形的边长为,
则.
解得:(不合题意,舍去),.
答:原来的正方形的边长为.
【点睛】本题考查了矩形的面积,一元二次方程的实际应用,根据题意列代数式和方程求解是解题的关键.
19.16或49
【分析】设一位数为,则两位数为,根据题意列出方程求解即可.
【详解】设一位数为,则两位数为.
则根据题意可得:,
整理得:.
分解得:,
解得:,.
答:这个两位数为16或49.
【点睛】本题考查了一元二次方程的应用,把一个一位数放在这个两位数的左边所成的三位数,可以表示为;把一个一位数放在这个两位数的右边所成的三位数,可以表示为,读懂题意,找出等量关系式是解题的关键.
20.(1)50千克,150千克;利润1300元
(2)将销售价定为每千克18元时,能使干枣平均每天的销售利润为200元
【分析】(1)设购进干枣千克,购进干枣千克,根据“水果店第一次用2500元直接购进这两种干枣共200千克”,列出二元一次方程组,解方程组即可得到答案;
(2)设干枣的售价定为每千克元,则每千克的销售利润为元,平均每天可售出千克,根据题意列出方程,解方程即可得到答案.
【详解】(1)解:设购进干枣千克,购进干枣千克,
根据题意可得:
,
解得:,
购进干枣50千克,购进干枣150千克,
利润为:(元);
(2)解:设干枣的售价定为每千克元,则每千克的销售利润为元,
平均每天可售出千克,
根据题意得:
,
整理得:,
解得:,
∵要给顾客优惠,
∴不符合题意舍去,
∴,
答:将销售价定为每千克18元时,能使干枣B平均每天的销售利润为200元.
【点睛】本题主要考查了二元一次方程组的应用、一元二次方程的应用,读懂题意,正确列出二元一次方程组和一元二次方程是解题的关键.
21.(1)
(2)该车刹车后秒内向前滑行了米
【分析】(1)待定系数法求解析式即可求解;
(2)根据题意得出,路程等于速度乘以时间,列出一元二次方程,解方程即可求解.
【详解】(1)解:将点,代入,
,
解得:,
∴与之间的函数关系式为;
(2)解:依题意,, ,,
则
依题意,,
即
解得:或(舍去)
答:该车刹车后秒内向前滑行了米.
【点睛】本题考查了一次函数的应用,一元二次方程的应用,根据题意列出一元二次方程,求得一次函数解析式是解题的关键.
22.(1)2秒或4秒
(2)3秒时,五边形的面积最小,最小值是39平方厘米
【分析】(1)设运动时间为,则,,再由面积公式建立方程求解即可;
(2)由(1)可得:要使的面积有最大值,则要使取最大值,则此时,面积为9, 则此时五边形的面积最小,从而可得答案.
【详解】(1)解:设运动时间为,则,,
则,
解得:或.
∴经过2秒或4秒时,的面积等于8平方厘米.
(2)由(1)可得:
∴要使的面积有最大值,则要使取最大值,则此时,面积为9,
则此时五边形的面积最小,最小值为.
【点睛】本题主要考查动点问题,一元二次方程的应用,配方法的应用,熟练的解一元二次方程是解本题的关键.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
人教版九年级数学上册
21.3 实际问题与一元二次方程 同步练习题
一、单选题
1.有一人患了流感,经过两轮传染后,共有人患了流感,每轮传染中平均每人传染了( )个人
A.11 B.12 C.13 D.14
2.海南省某企业年月份利润为万元,要使月份的利润为万元,则每月的平均增长率是( )
A. B. C. D.
3.某小区花园有一块长方形花圃,它的宽为,若长边不变,将短边扩大,使得扩大后的花圃形状为正方形,且面积比原来增加,设原来花圃长边为,可列方程( )
A. B.
C. D.
4.如图,这是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点…,第行有个点…,前行的点数和不能是以下哪个结果( )
A.45 B.66 C.100 D.210
5.某商店经销一种销售成本为40元的水果,据市场分析,若按每千克50元销售,一个月能售出500千克:销售单价每涨1元,月销售量就减少10千克,设销售单价为每千克()元,月销售利润达8000元.则方程为( )
A. B.
C. D.
6.在中,,动点P从点A沿线段向点B移动,一动点Q从点B沿线段向点C移动,两点同时开始移动,点的速度为,点的速度为,当到达点时两点同时停止运动.若使的面积为,则点P运动的时间是( )
A.1s B.4s C.5s或1s D.4s或1s
7.一辆汽车以20m/s的速度行驶,司机发现前方路面26m处有情况,紧急刹车后汽车又滑行25m后停车,问刹车后汽车滑行到16m时约用了( )
A.1s B.1.2s C.2s D.4s
8.如图,东西方向上有A,C两地相距10千米,甲以16千米/时的速度从A地出发向正东方向前进,乙以12千米/时的速度从C地出发向正南方向前进,那么最快经过( )小时,甲、乙两人相距6千米?
A. B. C.1.5 D.
9.根据下表提供的信息,一元二次方程的解大概是( )
2 3 4 5 6
5 13
A.0 B.3.5 C.3.8 D.4.5
10.如图,有一面积为的长方形鸡场,鸡场的一边靠墙(墙长),另三边用竹篱笆围成,如果竹篱笆的长为,设鸡场的垂直于墙的边长为,则下列方程正确的是( )
A. B.
C. D.
二、填空题
11.某学校组织篮球比赛,实行单循环制,共有36场比赛,则参加的队数为 .
12.如图,要设计一幅宽20cm,长30cm的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为,如果要使所有彩条所占面积为原矩形图案面积的三分之一,竖彩条的宽度是 cm.
13.2023“全晋乐购”网上年货节活动期间,某商家购进一批进价为80元/盒的吕梁沙棘汁,按150元/盒的价格进行销售,每天可售出160盒.后经市场调查发现,当每盒价格降低1元时,每天可多售出8盒.若要每天盈利16000元,设每盒价格降低元,则可列方程为 .
14.一个小球以速度开始向前滚动,并且均匀减速,后小球停止滚动.小球滚动约用了 秒(结果保留小数点后一位)
15.一个小组若干人,新年每人互送贺卡一张,已知全组共送贺卡30张,则这个小组有 人.
三、解答题
16.圣诞节昂立师生互送贺卡,总共送出张,求昂立共有师生多少人?
17.随着国家“惠民政策”的陆续出台,为了切实让老百姓得到实惠,国家卫计委通过严打药品销售环节中的不正当行为,以维护老百姓的利益.某种药品原价600元/瓶,经过连续两次降价后,现在仅卖384元/瓶.求该种药品平均每次降价的百分率.
18.将一个正方形的场地扩建,一边加长,一边加长后变成矩形,且矩形的面积是,求原来正方形的边长.
19.一个两位数是一个一位数的平方,把这个一位数放在这个两位数的左边所成的三位数,比把这个一位数放在这个两位数的右边所成的三位数大,求这个两位数.
20.在“五一”期间,某水果超市调查两种新疆干枣的销售情况,下面是调查员的对话:
小王:干枣的进价是每千克8元,售价16元,干枣的进价是每千克14元,售价20元.
小张:当干枣销售价每千克20元时,每天可售出30千克,若每千克降低1元,平均每天可多售出10千克.
根据他们的对话,解决下面所给的问题:
(1)该水果店第一次用2500元直接购进这两种干枣共200千克,问这两种干枣各购进多少千克?若全部售出,共获得多少利润?
(2)为了给顾客优惠,将销售价定为每千克多少元时,才能使干枣平均每天的销售利润为200元?
21.已知,一辆汽车在笔直的公路上刹车后,该车的速度米秒与时间秒之间满足一次函数关系,其图象如图所示;
(1)求与之间的函数关系式;
(2)已知汽车在该运动状态下,一段时间内向前滑行的距离等于这段时间内的平均速度乘以时间该运动状态下的平均速度,表示这段时间起始时刻的速度,表示这段时间结束时刻的速度.若该车刹车后秒内向前滑行了米,求的值.
22.如图,矩形中,,,点从开始沿边向点以厘米/秒的速度移动,点从点开始沿边向点以厘米/秒的速度移动,如果、分别是从同时出发,求经过几秒时,
(1)的面积等于平方厘米?
(2)五边形的面积最小?最小值是多少?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【分析】患流感的人把病毒传染给别人,自己仍然患病,包括在总数中.设每轮传染中平均一个人传染了x个人,则第一轮传染了x个人,第二轮作为传染源的是人,则传染人,依题意列方程:,解方程即可求解.
【详解】设每轮传染中平均一个人传染了x个人,依题意得
,即,
解方程得(舍去),
即每轮传染中平均每人传染了个人,
故选:B
【点睛】此题考查了一元二次方程的应用,解题的关键是读懂题目,从实际问题中抽象出方程模型,设出未知数,找出等量关系,列方程.
2.C
【分析】设每月的平均增长率是,由题意:月份利润为万元,要使月份的利润为万元,列出一元二次方程,解方程即可.
【详解】解:设每月的平均增长率是,
由题意得:,
解得:,不符合题意,舍去.
即每月的平均增长率是,
故选:C.
【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
3.B
【分析】设原来花圃长边为,则短边增加了,再根据面积增加了列出方程即可.
【详解】解:,设原来花圃长边为,则短边增加了,
由题意得,,即,
故选B.
【点睛】本题主要考查了从实际问题中抽象出一元二次方程,正确理解题意找到等量关系是解题的关键.
4.C
【分析】由于第一行有1个点,第二行有2个点…第n行有n个点…,则前n行共有个点,然后根据选项分别求出n的值,即可作出判断.
【详解】通过观察图形可知:第一行有1个点,第二行有2个点…第n行有n个点,
前n行共有个点,其中n为正整数.
∴当时,解得:(舍去),;
当时,解得:(舍去), ;
当时,解得:(舍去),(舍去),即前行的点数和不能是100;
当时,解得:(舍去),.
故选:C.
【点睛】本题主要考查的是探究图形的规律,一元二次方程的解.正确得到前行的点数和的式子是解题的关键.
5.A
【分析】根据题意销售单价每涨1元,月销售量就减少10千克,得到销售单价为时销量为:,再根据:利润(单价成本)数量,列出方程即可得出答案.
【详解】解:售价为时的销量为:,
月销售利润达8000时得:,
故答案选:A.
【点睛】本题考查了一元二次方程的应用,理解题意找出数量关系列出方程是解题关键.
6.A
【分析】设点运动的时间为,则,,利用三角形的面积计算公式,即可得出关于的一元二次方程,解之即可得出的值,再结合当到达点时两点同时停止运动,即可得出点运动的时间.
【详解】解:设点运动的时间为,则,,
依题意得:,
整理得:,
解得:,,
当到达点时两点同时停止运动,
,
,
.
故选:A.
【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
7.A
【分析】等量关系为:平均速度×时间=16,把相关数值代入即可求解.
【详解】解:设约用了x秒.
汽车每秒减少的速度为:20÷[25÷(20÷2)]=8,
∴16米时的平均速度为:[20+(20﹣8x)]÷2=20﹣4x.
∴(20﹣4x)×x=16,
解得:x1=1,x2=4,
∵20﹣8x>0,
∴x=1,
故选:A.
【点睛】本题考查了一元二次方程的应用,用到的知识点为:匀变速运动的物体的平均速度=初速度与末速度和的一半;每秒减少的速度等于初速度与末速度之差与所用时间的比值.
8.A
【分析】根据题意表示出BC,DC的长,进而利用勾股定理求出答案
【详解】解:设最快经过x小时,甲、乙两人相距6km,根据题意可得:
BC=(10﹣16x)km,DC=12xkm,
因为BC2+DC2=BD2,
则(10﹣16x)2+(12x)2=62,
解得:x1=x2=0.4.
答:最快经过0.4小时,甲、乙两人相距6km.
故选A.
【点睛】此题主要考查了勾股定理以及一元二次方程的应用,利用勾股定理列出方程是解题的关键.
9.D
【分析】根据表格数据,找出代数式从变为时的取值范围即可判断
【详解】时,,
时,,
则的解的范围为,
即一元二次方程的解大概是4.5.
故选D.
【点睛】本题考查了估算一元二次方程的解的近似值,根据表格获得信息是解题的关键.
10.C
【分析】已知长方形鸡场垂直于墙的边长(即长方形鸡场的宽)为,结合竹篱笆的长度,可求得长方形鸡场的长,根据面积的等量关系,可列出方程.
【详解】解:设鸡场的垂直于墙的边长为,鸡场平行于墙的边长为:,
根据面积的等量关系,得:
.
故选:C.
【点睛】本题主要考查列二元一次方程,根据题意找到等量关系并用未知数表示出来是解题的关键.
11.9
【分析】设有个球队参加比赛,那么第一个队和其他队打场球,第二个队和其他队打场,以此类推可以知道共打场,然后列出方程求解.
【详解】解:设邀请个球队参加比赛,
依题意得,
即,
,
或(不合题意,舍去).
故答案为:9.
【点睛】此题考查了一元二次方程的应用,该题和实际生活结合比较紧密,准确找到关键描述语,从而根据等量关系准确地列出方程是解决问题的关键.此题还要判断所求的解是否符合题意,舍去不合题意的解.
12.
【分析】设横彩条的宽度为,则竖彩条的宽度为,则由图可知一个横彩条的面积为,一个竖彩条的面积为,重叠的面积为,接下来根据所有彩条所占面积为原矩形图案面积的三分之一可得,解方程,问题便可解答.
【详解】解:设横彩条的宽度为,则竖彩条的宽度为,则
,
解得,(舍去),
∴,
∴竖的彩条宽为.
故答案为:.
【点睛】本题属于一元二次方程的应用,找出等量关系是解答本题的关键.
13.
【分析】设每件商品售价降低元,根据“每天盈利16000元”列出一元二次方程即可.
【详解】解:设每件商品售价降低元,平均每天可售出盒.
依题意得:,
故答案为:.
【点睛】本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
14.1.2.
【分析】利用等量关系:速度时间=路程,时间为,根据题意列出方程:求解即可.
【详解】由题意得:小球的平均滚动速度是,
设小球滚动5时约用了,
由题意得:,
整理得:,
解得:,
∵,
∴,
故小球滚动用了1.2秒.
【点睛】本题考查了一元二次方程的应用,重点在于求出平均每秒小球的运动减少的速度,读懂题意是解题的关键.
15.6
【分析】设这个小组有x个人,则每个人送出张贺卡,再根据全组共送贺卡30张建立方程求解即可.
【详解】解:设这个小组有x个人,
由题意得:
解得(舍去),
∴这个小组有6人
故答案为:6.
【点睛】本题主要考查了一元二次方程的事件应用,根据每个人送出张贺卡建立方程是解题的关键.
16.31人
【分析】设昂立共有师生人,再建立方程:,再解方程即可.
【详解】解:设昂立共有师生人,
由题意可得:,
整理得:,解得:,(负值舍去).
答:昂立共有师生31人.
【点睛】本题主要考查互送卡片问题,一元二次方程的应用,确定相等关系是解本题的关键,注意由于每人都要送到,因此不用除2.
17.20%
【分析】设该种药品平均每次降价的百分率为x,则第一次降价后的单价是原来的,第二次降价后的单价是原来的,根据题意列方程解答即可.
【详解】解:设该种药品平均每次降价的百分率为,
由题意得:,
解得:,(不合题意舍去),
∴,
答:该种药品平均每次降价的百分率为20%.
【点睛】此题主要考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
18.
【分析】先原来的正方形的边长为,则一边长为:,另一边长为:,根据题意列出方程,解方程即可.
【详解】解:设原来的正方形的边长为,
则.
解得:(不合题意,舍去),.
答:原来的正方形的边长为.
【点睛】本题考查了矩形的面积,一元二次方程的实际应用,根据题意列代数式和方程求解是解题的关键.
19.16或49
【分析】设一位数为,则两位数为,根据题意列出方程求解即可.
【详解】设一位数为,则两位数为.
则根据题意可得:,
整理得:.
分解得:,
解得:,.
答:这个两位数为16或49.
【点睛】本题考查了一元二次方程的应用,把一个一位数放在这个两位数的左边所成的三位数,可以表示为;把一个一位数放在这个两位数的右边所成的三位数,可以表示为,读懂题意,找出等量关系式是解题的关键.
20.(1)50千克,150千克;利润1300元
(2)将销售价定为每千克18元时,能使干枣平均每天的销售利润为200元
【分析】(1)设购进干枣千克,购进干枣千克,根据“水果店第一次用2500元直接购进这两种干枣共200千克”,列出二元一次方程组,解方程组即可得到答案;
(2)设干枣的售价定为每千克元,则每千克的销售利润为元,平均每天可售出千克,根据题意列出方程,解方程即可得到答案.
【详解】(1)解:设购进干枣千克,购进干枣千克,
根据题意可得:
,
解得:,
购进干枣50千克,购进干枣150千克,
利润为:(元);
(2)解:设干枣的售价定为每千克元,则每千克的销售利润为元,
平均每天可售出千克,
根据题意得:
,
整理得:,
解得:,
∵要给顾客优惠,
∴不符合题意舍去,
∴,
答:将销售价定为每千克18元时,能使干枣B平均每天的销售利润为200元.
【点睛】本题主要考查了二元一次方程组的应用、一元二次方程的应用,读懂题意,正确列出二元一次方程组和一元二次方程是解题的关键.
21.(1)
(2)该车刹车后秒内向前滑行了米
【分析】(1)待定系数法求解析式即可求解;
(2)根据题意得出,路程等于速度乘以时间,列出一元二次方程,解方程即可求解.
【详解】(1)解:将点,代入,
,
解得:,
∴与之间的函数关系式为;
(2)解:依题意,, ,,
则
依题意,,
即
解得:或(舍去)
答:该车刹车后秒内向前滑行了米.
【点睛】本题考查了一次函数的应用,一元二次方程的应用,根据题意列出一元二次方程,求得一次函数解析式是解题的关键.
22.(1)2秒或4秒
(2)3秒时,五边形的面积最小,最小值是39平方厘米
【分析】(1)设运动时间为,则,,再由面积公式建立方程求解即可;
(2)由(1)可得:要使的面积有最大值,则要使取最大值,则此时,面积为9, 则此时五边形的面积最小,从而可得答案.
【详解】(1)解:设运动时间为,则,,
则,
解得:或.
∴经过2秒或4秒时,的面积等于8平方厘米.
(2)由(1)可得:
∴要使的面积有最大值,则要使取最大值,则此时,面积为9,
则此时五边形的面积最小,最小值为.
【点睛】本题主要考查动点问题,一元二次方程的应用,配方法的应用,熟练的解一元二次方程是解本题的关键.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
