22.3 实际问题与二次函数同步练习题(含解析)
文档属性
| 名称 | 22.3 实际问题与二次函数同步练习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-04 22:49:48 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
人教版 九年级数学上册
22.3 实际问题与二次函数 同步练习题
一、单选题
1.下列三个问题中都有两个变量:①把一个长10cm、宽5cm的长方形的长减少xcm,宽不变,长方形的面积y(单位:)随x的变化而变化;②一个矩形绿地的长为30m,宽为20m,若长和宽各增加xm,则扩充后的绿地的面积y(单位:)随x的变化而变化;③某长方体的体积为1000,长方体的高y(单位:cm)随底面积x(单位:)的变化而变化;则y关于x的函数关系正确的是( )
A.①二次函数,②二次函数,③二次函数
B.①一次函数,②二次函数,③反比例函数
C.①二次函数,②二次函数,③一次函数
D.①反比例函数,②二次函数,③一次函数
2.如图,要围一个矩形菜园,共中一边是墙,且的长不能超过,其余的三边用篱笆,且这三边的和为.有下列结论:
①的长可以为;
②的长有两个不同的值满足菜园面积为;
③菜园面积的最大值为.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
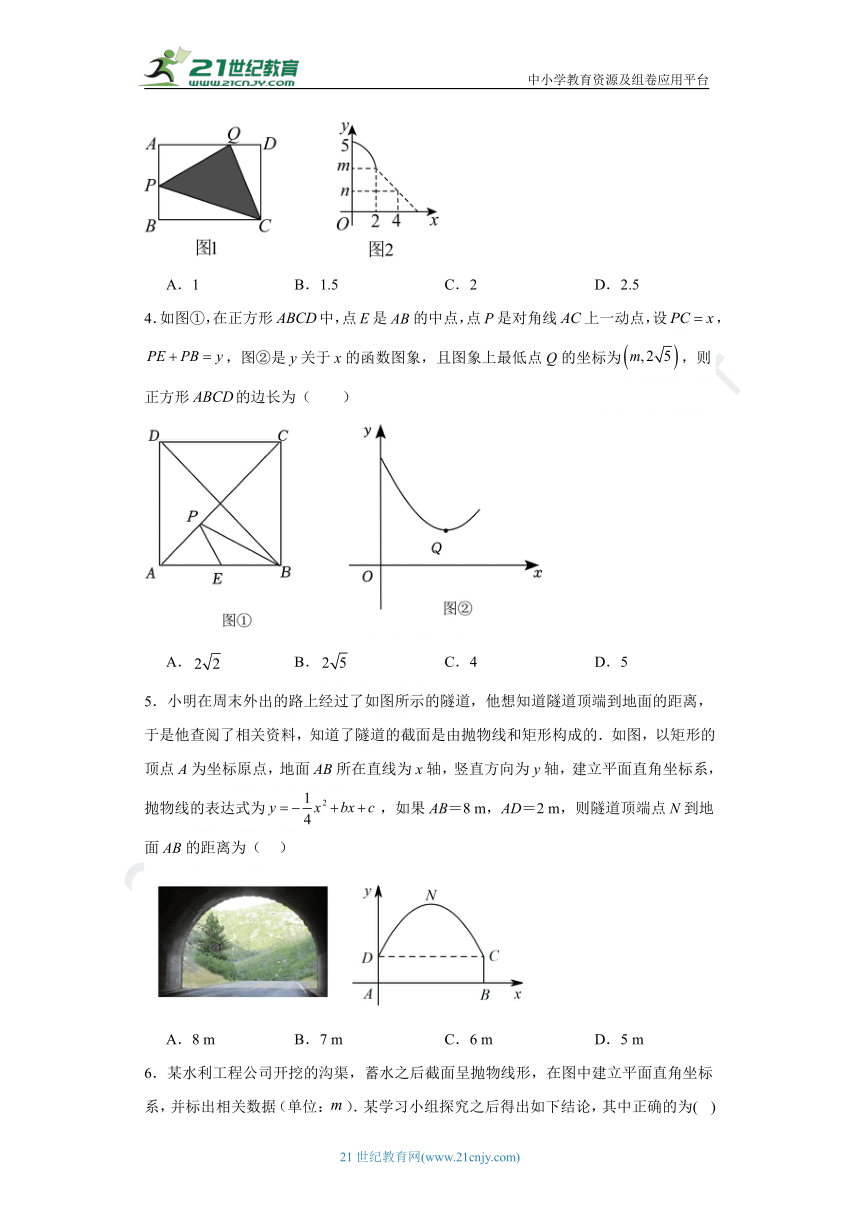
3.如图1,在矩形()中,动点Q从点D出发,沿以每秒1个单位长度的速度做匀速运动,到达点A后停止运动,动点P从点B出发,沿以与点Q同样的速度做匀速运动,到达点A后也停止运动.已知点P,Q同时开始运动,设点Q的运动时间为x秒,的面积是y,其中y关于x的函数图像如图2所示,则的值是( )
A.1 B.1.5 C.2 D.2.5
4.如图①,在正方形中,点E是的中点,点P是对角线上一动点,设,,图②是y关于x的函数图象,且图象上最低点Q的坐标为,则正方形的边长为( )
A. B. C.4 D.5
5.小明在周末外出的路上经过了如图所示的隧道,他想知道隧道顶端到地面的距离,于是他查阅了相关资料,知道了隧道的截面是由抛物线和矩形构成的.如图,以矩形的顶点A为坐标原点,地面AB所在直线为x轴,竖直方向为y轴,建立平面直角坐标系,抛物线的表达式为,如果AB=8 m,AD=2 m,则隧道顶端点N到地面AB的距离为( )
A.8 m B.7 m C.6 m D.5 m
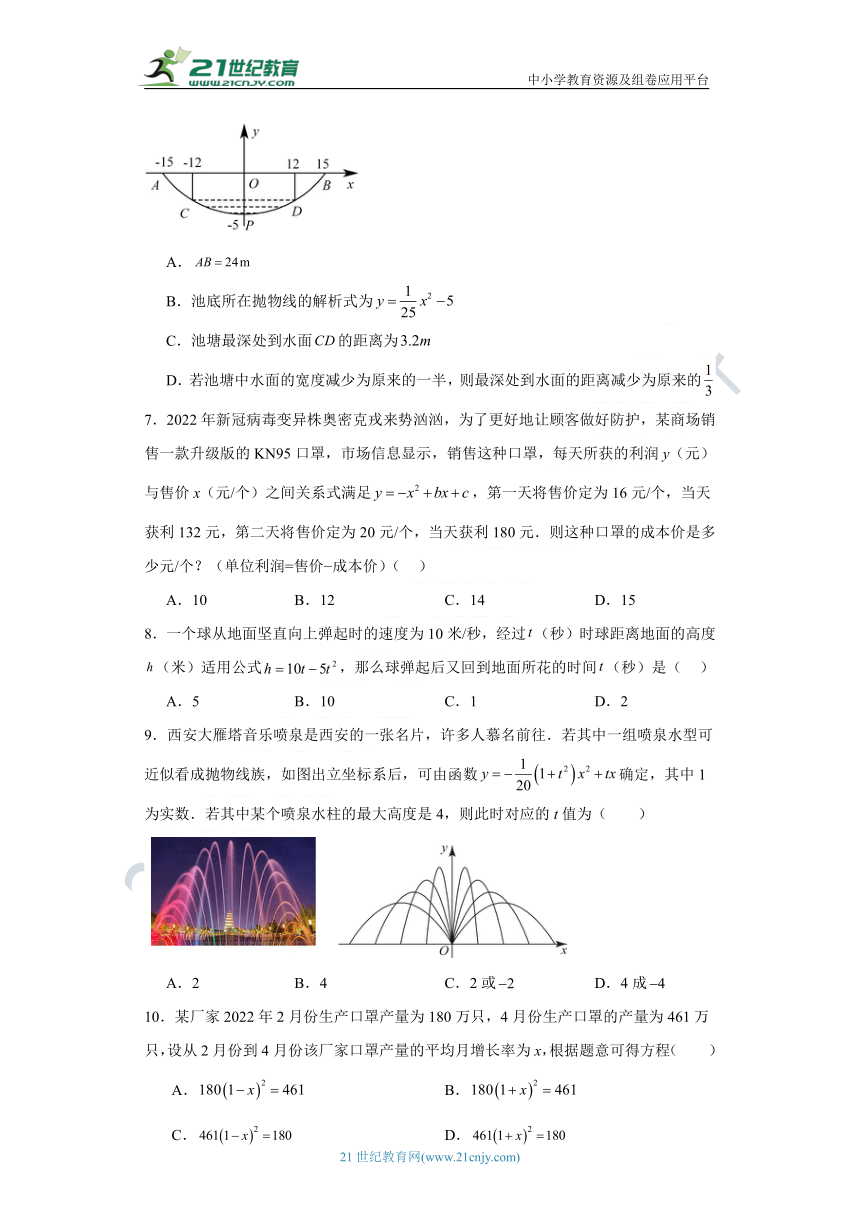
6.某水利工程公司开挖的沟渠,蓄水之后截面呈抛物线形,在图中建立平面直角坐标系,并标出相关数据(单位:).某学习小组探究之后得出如下结论,其中正确的为( )
A.
B.池底所在抛物线的解析式为
C.池塘最深处到水面的距离为
D.若池塘中水面的宽度减少为原来的一半,则最深处到水面的距离减少为原来的
7.2022年新冠病毒变异株奥密克戎来势汹汹,为了更好地让顾客做好防护,某商场销售一款升级版的KN95口罩,市场信息显示,销售这种口罩,每天所获的利润y(元)与售价x(元/个)之间关系式满足,第一天将售价定为16元/个,当天获利132元,第二天将售价定为20元/个,当天获利180元.则这种口罩的成本价是多少元/个?(单位利润=售价 成本价)( )
A.10 B.12 C.14 D.15
8.一个球从地面坚直向上弹起时的速度为10米/秒,经过(秒)时球距离地面的高度(米)适用公式,那么球弹起后又回到地面所花的时间(秒)是( )
A.5 B.10 C.1 D.2
9.西安大雁塔音乐喷泉是西安的一张名片,许多人慕名前往.若其中一组喷泉水型可近似看成抛物线族,如图出立坐标系后,可由函数确定,其中1为实数.若其中某个喷泉水柱的最大高度是4,则此时对应的t值为( )
A.2 B.4 C.2或 D.4成
10.某厂家2022年2月份生产口罩产量为180万只,4月份生产口罩的产量为461万只,设从2月份到4月份该厂家口罩产量的平均月增长率为x,根据题意可得方程( )
A. B.
C. D.
二、填空题
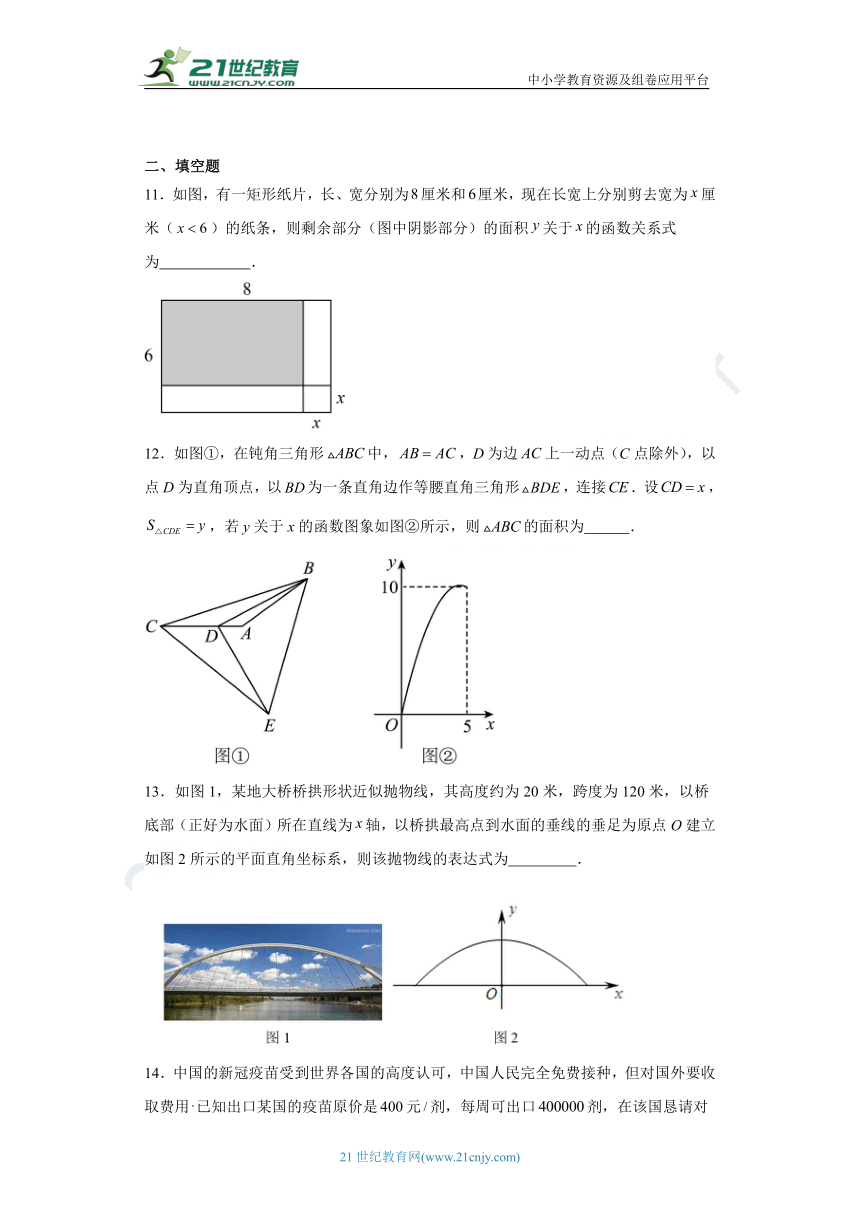
11.如图,有一矩形纸片,长、宽分别为厘米和厘米,现在长宽上分别剪去宽为厘米()的纸条,则剩余部分(图中阴影部分)的面积关于的函数关系式为 .
12.如图①,在钝角三角形中,,D为边上一动点(C点除外),以点D为直角顶点,以为一条直角边作等腰直角三角形,连接.设,,若y关于x的函数图象如图②所示,则的面积为 .
13.如图1,某地大桥桥拱形状近似抛物线,其高度约为20米,跨度为120米,以桥底部(正好为水面)所在直线为轴,以桥拱最高点到水面的垂线的垂足为原点O建立如图2所示的平面直角坐标系,则该抛物线的表达式为 .
14.中国的新冠疫苗受到世界各国的高度认可,中国人民完全免费接种,但对国外要收取费用已知出口某国的疫苗原价是元剂,每周可出口剂,在该国恳请对其优惠销售的条件下,每剂的售价每降低元,每周可多出口剂,设出口疫苗的销售收入为元,销售价格为元剂,则与之间的函数表达式为 .
15.某厂七月份的产值是10万元,设第三季度每个月产值的增长率相同,都为x(x>0),九月份的产值为y万元,那么y关于x的函数解析式为 .(不要求写定义域)
三、解答题
16.某商店进购一商品,第一天每件盈利(毛利润)10元,销售500件.
(1)第二、三天该商品十分畅销.销售量持续走高.在售价不变的基础上,第二、三天的销售量达到605件,求第二、三天的日平均增长率;
(2)经市场调查发现,在进货价不变的情况下,若每件涨价1元,日销量将减少20件.
①现要保证每天总毛利润6000元,同时又要使顾客得到实惠,则每件应张价多少元?
②现需按毛利润的交纳各种税费,人工费每日按销售量每件支出0.9元,水电房租费每日102元,若剩下的每天总纯利润要达到5100元,则每件涨价应为多少?
17.芯片行业是制约我国工业发展的主要技术之一.经过大量科研、技术人员艰苦攻关,我国芯片有了新突破.某芯片实现国产化后,芯片价格大幅下降.原来每片芯片的单价为元,准备进行两次降价,如果每次降价的百分率都为,经过两次降价后的价格为(元).
(1)求与之间的函数关系式;
(2)如果该芯片经过两次降价后每片芯片单价为元,求每次降价的百分率.
18.某种产品现在的年产量是,计划今后两年增加产量.如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示?
19.某商场第1年销售计算机5000台,如果每年的销售量比上一年增加相同的百分率x,写出第3年的销售量y关于每年增加的百分率x的函数解析式.
20.为积极响应国家“旧房改造”工程,该市推出《加快推进旧房改造工作的实施方案》推进新型城镇化建设,改善民生,优化城市建设.
(1)根据方案该市的旧房改造户数从2020年底的3万户增长到2022年底的4.32万户,求该市这两年旧房改造户数的平均年增长率;
(2)该市计划对某小区进行旧房改造,如果计划改造300户,计划投入改造费用平均20000元/户,且计划改造的户数每增加1户,投入改造费平均减少50元/户,求旧房改造申报的最高投入费用是多少元?
21.某公司的生产利润原来是万元,经过连续两年的增长达到了万元,如果每年增长率都是,写出利润与增长的百分率之间的函数解析式,它是什么函数?
22.某工厂前年的生产总值为10万元,去年比前年的年增长率为x,预计今年比去年的年增长率仍为x,今年的总产值为y万元.
(1)求y关于x的函数关系式.
(2)当x=20%时,今年的总产值为多少?
(3)在(2)的条件下,前年、去年和今年三年的总产值为多少万元?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【分析】根据题意,分别求出相应的函数解析式,进行判断即可;
【详解】解:①由题意,得:,故①是一次函数;
②由题意,得:,故②是二次函数;
③由题意,得:,故①是反比例函数;
故选B.
【点睛】本题考查列函数关系式.解题的关键是正确的列出函数关系式.
2.C
【分析】设的长为,矩形的面积为,则的长为,根据矩形的面积公式列二次函数解析式,再分别根据的长不能超过,二次函数的最值,解一元二次方程求解即可.
【详解】设的长为,矩形的面积为,则的长为,由题意得
,
其中,即,
①的长不可以为,原说法错误;
③菜园面积的最大值为,原说法正确;
②当时,解得或,
∴的长有两个不同的值满足菜园面积为,说法正确;
综上,正确结论的个数是2个,
故选:C.
【点睛】本题考查了二次函数的应用,解一元二次方程,准确理解题意,列出二次函数解析式是解题的关键.
3.C
【分析】设,分和,结合矩形的性质,表示三角形的面积,构造函数,结合图像,确定m,n的值计算即可.
【详解】解:设,
当时,,
根据图像,得当时,y取得最大值5,此时,
当时,,此时;
当时,P停止运动,
,
根据图像,当时,此时,
故,
故选:C.
【点睛】本题考查了数形结合思想,二次函数的最值,一次函数的性质,熟练掌握二次函数的最值,一次函数的性质是解题的关键.
4.C
【分析】如图,点D是点B关于直线的对称点,连接交于点P,则此时y取得最小值,即,即可求解.
【详解】解:如图,点D是点B关于直线的对称点,连接交于点P,
根据点的对称性,,则为最小,
故,
设正方形的边长为a,则,
在中,由勾股定理得:,
即,
解得:(负值已舍去),
故选:C.
【点睛】本题考查的是动点图象问题,涉及到二次函数、解直角三角形,正方形的性质,利用勾股定理求线段长是解题的关键.
5.C
【分析】根据条件易有点坐标为,点的坐标为,点的横坐标为4,将点和代入抛物线表达式可解的和的值,然后令计算点的纵坐标即为距离.
【详解】解:由题意可得:点坐标为,点的坐标为,
将点和代入抛物线表达式可得,解得
∴,
令,可得.
故选:C.
【点睛】本题主要考查二次函数的实际应用,能够根据条件得到对应点的坐标,解出抛物线表达式是解题的关键,然后在将实际问题转化为二次函数点的坐标问题.
6.C
【分析】利用建立的坐标系得到抛物线上点的坐标,然后通过待定系数法求出抛物线解析式,对照选项即可.
【详解】设解析式为,抛物线上点,,,带入抛物线解析式中得,解得,解析式为.
选项A中,,故选项A错误;
选项B中,解析式为,故选项B错误;
选项C中,池塘水深最深处为点,水面,,所以水深最深处为点P到水面的距离为3.2米,故选项C正确;
选项D中,若池塘中水面的宽度减少为原来的一半,由抛物线关于轴对称可知,抛物线上点横坐标,带入解析式算得,即到水面距离为米,而最深处到水面的距离为3.2米,减少为原来的.故选项D错误.
故选C.
【点睛】本题考查二次函数的实际应用问题,计算较为复杂,在计算时需要理清楚实际数据在坐标系中对应的位置.能够正确计算和分析实际情况是解题的关键.
7.A
【分析】根据题意列方程组求出二次函数的解析式,再列方程即可得到结论.
【详解】解:由题意知:当时,;当时,代入中,
得,
解得:,
∴,
当每天利润为0元时,售价即为成本价.令,
解得:,
由题意可知38不符合条件,
∴,
∴这种口罩的成本价是10元/个;
故选:A.
【点睛】本题考查了二次函数的应用,一元二次方程的应用,正确的理解题意是解题的关键.
8.D
【分析】根据球弹起后又回到地面时,得到,解方程即可得到答案.
【详解】解:球弹起后又回到地面时,即,
解得(不合题意,舍去),,
∴球弹起后又回到地面所花的时间(秒)是2,
故选:D
【点睛】此题考查了求二次函数自变量的值,读懂题意,得到方程是解题的关键.
9.C
【分析】由可得其对称轴为:,当时,,即有,解方程即可求解.
【详解】由可得其对称轴为:,
根据,
可知:当时,,
即有:,
解得:,
故选:C.
【点睛】本题考查了二次函数的图象与性质以及二次函数的应用等知识,明确题意,得出当时,,是解答本题的关键.
10.B
【分析】利用4月份该厂家口罩产量月份该厂家口罩产量从2月份到4月份该厂家口罩产量的平均月增长率,即可得出关于x的一元二次方程,此题得解.
【详解】解:根据题意得,
故选:B.
【点睛】本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
11.
【分析】阴影部分的长方形的的长为,宽为,然后根据长方形的面积公式即可求解.
【详解】阴影部分的长方形的的长为,宽为,
所以面积.
【点睛】本题考查了利用长方形的面积公式列出函数关系式,其中根据题意,找到所求量的等量关系是解决问题的关键.
12.
【分析】由②知,最大为5,此时点D与点A重合,,过点E作,交延长线于G,根据等腰三角形的性质及三角形等面积法得出,过点B作,交延长线于H,则,再由全等三角形的判定和性质得出,即可求解三角形面积.
【详解】解:由②知,最大为5,此时点D与点A重合,,
∵是等腰直角三角形,
∴,
过点E作,交延长线于G,
∴,
解得,
∴
过点B作,交延长线于H,则,
∵
∴,
∵,
∴,
∴,
∴
故答案为:.
【点睛】此题考查了动点问题与函数图象的结合,二次函数的图象和性质,全等三角形的判定和性质,综合掌握各知识点是解题的关键.
13.
【分析】设抛物线解析式为,根据题意可得,抛物线与x轴两交点坐标分别为、,代入即可求出.
【详解】解:设抛物线解析式为,
由题意可知:,抛物线与x轴两交点坐标分别为、,
把、,代入得:,
解得:,
∴抛物线解析式为,
故答案为:.
【点睛】本题考查了求抛物线解析式,正确设出解析式和确定点的坐标是解题关键.
14.
【分析】根据利润=每件利润×销量求解.
【详解】解:由题意得,
故答案为:.
【点睛】本题考查二次函数的应用,解题关键是根据题意列出函数解析式.
15.y=10(1+x)2
【分析】利用该厂九月份的产值=该厂七月份的产值×(1+增长率)2,即可得出结论.
【详解】解:∵该厂七月份的产值是10万元,且第三季度每个月产值的增长率相同,均为x,
∴该厂八月份的产值是10(1+x)万元,九月份的产值是10(1+x)2万元,
∴y=10(1+x)2.
故答案为:y=10(1+x)2.
【点睛】本题考查了由根据实际问题列二次函数关系式,根据各数量之间的关系,正确列出二次函数关系式是解题的关键.
16.(1)
(2)①每件应张价5元;②每件涨价应为8元
【分析】(1)设第二、三天的日平均增长率为x,利用第三天的销售量=第一天的销售量,即可得出关于x的一元二次方程,解之取其正值即可得出结论;
(2)①设每件应张价y元,则每件盈利(毛利润)为元,销售数量为件,根据每件盈利(毛利润)×销售数量=每天总毛利润列方程求解即可;
②设每件涨价应为z元,则每天总毛利润为元,每天总纯利润为元,根据每天总纯利润要达到5100元,列方程求解即可.
【详解】(1)解: 设第二、三天的日平均增长率为x,根据题意,得
,
解得: , (不符合题意,舍去),
∴,
答: 第二、三天的日平均增长率为10%.
(2)解:①设每件应张价y元,根据题意,得
,
解得:,,
∵要使顾客得到实惠,
∴,
答:每件应张价5元;
②设每件涨价应为z元,根据题意,得
,
解得:,
∴,
答:每件涨价应为8元.
【点睛】本题考查一元二次方程的应用,理解题意,设恰当未知数,找出等量关系,列出方程是解题的关键.
17.(1)
(2)
【分析】(1)利用经过两次降价后的价格原价每次降价的百分率,即可找出与之间了函数关系式;
(2)根据该芯片经过两次降价后每块芯片单价为元,即可得出关于的一元二次方程,解之取其符合题意的值即可得出结论.
【详解】(1)∵每次降价的百分率都为,经过两次降价后的价格为(元)
∴依题意得:,
∴与之间的函数关系式为;
(2)依题意得:,
解得:,(不符合题意,舍去),
∴每次降价的百分率为20%.
【点睛】本题考查了一元二次方程的应用以及二次函数关系式,解题的关键是:(1)根据各数量之间的关系,找出y关于x的函数关系式;(2)找准等量关系,正确列出一元二次方程.
18.,y是x的函数
【分析】根据题意可得一年后的产量是,再经过一年后的产量是,由此求解即可.
【详解】解:这种产品的原产量是,一年后的产量是,再经过一年后的产量是,即两年后的产量,
即①
①式表示了两年后的产量y与计划增产的倍数x之间的关系,对于x的每一个值,y都有一个对应值,即y是x的函数.
【电锯】本题考查了函数关系式,利用增长问题获得函数解析式是解题关键,注意增加x倍是原来的(x+1)倍.
19.y=5000x2+10000x+5000.
【分析】根据增长率第2年的销量=第1年的销量+增加百分率x×第1年的销量=(1+x)×第1年的销量,第3年的销售量y=第2年的销量+增加百分率x×第2年的销量=(1+x)×第2年的销量=(1+x)2×第1年的销量即可.
【详解】解:由题意可知y=500(1+x)2=5000x2+10000x+5000,
∴y=5000x2+10000x+5000.
【点睛】本题考查增长率问题,利用增长率求函数解析式,掌握增长率的公式是解题关键.
20.(1)20%;(2)6125000(元)
【分析】(1)设平均增长率为x,根据题意列式求解即可;
(2)设多改造y户,最高投入费用为w元,根据题意列式,然后根据二次函数的性质即可求出最大值.
【详解】解:(1)设平均增长率为x,则x>0,
由题意得:,
解得:x=0.2或x=-2.2(舍),
答:该市这两年旧房改造户数的平均年增长率为20%;
(2)设多改造a户,最高投入费用为w元,
由题意得:,
∵a=-50,抛物线开口向下,
∴当a-50=0,即a=50时,w最大,此时w=612500元,
答:旧房改造申报的最高投入费用为612500元.
【点睛】本题考查二次函数的实际应用,解题的关键是正确读懂题意列出式子,然后根据二次函数的性质进行求解.
21.见解析.
【分析】根据增长率的问题,基数是a元,增长次数2次,结果为y,根据增长率的公式表示函数关系式.
【详解】依题意,得:,
此函数是二次函数.
【点睛】此题主要考查了根据实际问题列二次函数关系式,在表示增长率问题时,要明确基数,增长次数,最后的结果.
22.(1);(2)万元;(3)万元.
【分析】(1)根据题意列式为y=10×(1+x)×(1+x)= 10(1+x) ;(2)把x的值代入(1)求解即可;(3)代入求解即可.
【详解】(1)根据题意列式为y=10×(1+x)×(1+x)=10(1+x) ;
(2)当x=20%时,今年的总产值=10(1+20%) =14.4万元;
(3) 依题意,得前年,去年和今年三年的总产值为:10+10(1+20%)+ 10(1+x) =36.4(万元).
【点睛】本题考查了二次函数的应用,解题的关键是将实际问题转化为二次函数求解.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
人教版 九年级数学上册
22.3 实际问题与二次函数 同步练习题
一、单选题
1.下列三个问题中都有两个变量:①把一个长10cm、宽5cm的长方形的长减少xcm,宽不变,长方形的面积y(单位:)随x的变化而变化;②一个矩形绿地的长为30m,宽为20m,若长和宽各增加xm,则扩充后的绿地的面积y(单位:)随x的变化而变化;③某长方体的体积为1000,长方体的高y(单位:cm)随底面积x(单位:)的变化而变化;则y关于x的函数关系正确的是( )
A.①二次函数,②二次函数,③二次函数
B.①一次函数,②二次函数,③反比例函数
C.①二次函数,②二次函数,③一次函数
D.①反比例函数,②二次函数,③一次函数
2.如图,要围一个矩形菜园,共中一边是墙,且的长不能超过,其余的三边用篱笆,且这三边的和为.有下列结论:
①的长可以为;
②的长有两个不同的值满足菜园面积为;
③菜园面积的最大值为.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
3.如图1,在矩形()中,动点Q从点D出发,沿以每秒1个单位长度的速度做匀速运动,到达点A后停止运动,动点P从点B出发,沿以与点Q同样的速度做匀速运动,到达点A后也停止运动.已知点P,Q同时开始运动,设点Q的运动时间为x秒,的面积是y,其中y关于x的函数图像如图2所示,则的值是( )
A.1 B.1.5 C.2 D.2.5
4.如图①,在正方形中,点E是的中点,点P是对角线上一动点,设,,图②是y关于x的函数图象,且图象上最低点Q的坐标为,则正方形的边长为( )
A. B. C.4 D.5
5.小明在周末外出的路上经过了如图所示的隧道,他想知道隧道顶端到地面的距离,于是他查阅了相关资料,知道了隧道的截面是由抛物线和矩形构成的.如图,以矩形的顶点A为坐标原点,地面AB所在直线为x轴,竖直方向为y轴,建立平面直角坐标系,抛物线的表达式为,如果AB=8 m,AD=2 m,则隧道顶端点N到地面AB的距离为( )
A.8 m B.7 m C.6 m D.5 m
6.某水利工程公司开挖的沟渠,蓄水之后截面呈抛物线形,在图中建立平面直角坐标系,并标出相关数据(单位:).某学习小组探究之后得出如下结论,其中正确的为( )
A.
B.池底所在抛物线的解析式为
C.池塘最深处到水面的距离为
D.若池塘中水面的宽度减少为原来的一半,则最深处到水面的距离减少为原来的
7.2022年新冠病毒变异株奥密克戎来势汹汹,为了更好地让顾客做好防护,某商场销售一款升级版的KN95口罩,市场信息显示,销售这种口罩,每天所获的利润y(元)与售价x(元/个)之间关系式满足,第一天将售价定为16元/个,当天获利132元,第二天将售价定为20元/个,当天获利180元.则这种口罩的成本价是多少元/个?(单位利润=售价 成本价)( )
A.10 B.12 C.14 D.15
8.一个球从地面坚直向上弹起时的速度为10米/秒,经过(秒)时球距离地面的高度(米)适用公式,那么球弹起后又回到地面所花的时间(秒)是( )
A.5 B.10 C.1 D.2
9.西安大雁塔音乐喷泉是西安的一张名片,许多人慕名前往.若其中一组喷泉水型可近似看成抛物线族,如图出立坐标系后,可由函数确定,其中1为实数.若其中某个喷泉水柱的最大高度是4,则此时对应的t值为( )
A.2 B.4 C.2或 D.4成
10.某厂家2022年2月份生产口罩产量为180万只,4月份生产口罩的产量为461万只,设从2月份到4月份该厂家口罩产量的平均月增长率为x,根据题意可得方程( )
A. B.
C. D.
二、填空题
11.如图,有一矩形纸片,长、宽分别为厘米和厘米,现在长宽上分别剪去宽为厘米()的纸条,则剩余部分(图中阴影部分)的面积关于的函数关系式为 .
12.如图①,在钝角三角形中,,D为边上一动点(C点除外),以点D为直角顶点,以为一条直角边作等腰直角三角形,连接.设,,若y关于x的函数图象如图②所示,则的面积为 .
13.如图1,某地大桥桥拱形状近似抛物线,其高度约为20米,跨度为120米,以桥底部(正好为水面)所在直线为轴,以桥拱最高点到水面的垂线的垂足为原点O建立如图2所示的平面直角坐标系,则该抛物线的表达式为 .
14.中国的新冠疫苗受到世界各国的高度认可,中国人民完全免费接种,但对国外要收取费用已知出口某国的疫苗原价是元剂,每周可出口剂,在该国恳请对其优惠销售的条件下,每剂的售价每降低元,每周可多出口剂,设出口疫苗的销售收入为元,销售价格为元剂,则与之间的函数表达式为 .
15.某厂七月份的产值是10万元,设第三季度每个月产值的增长率相同,都为x(x>0),九月份的产值为y万元,那么y关于x的函数解析式为 .(不要求写定义域)
三、解答题
16.某商店进购一商品,第一天每件盈利(毛利润)10元,销售500件.
(1)第二、三天该商品十分畅销.销售量持续走高.在售价不变的基础上,第二、三天的销售量达到605件,求第二、三天的日平均增长率;
(2)经市场调查发现,在进货价不变的情况下,若每件涨价1元,日销量将减少20件.
①现要保证每天总毛利润6000元,同时又要使顾客得到实惠,则每件应张价多少元?
②现需按毛利润的交纳各种税费,人工费每日按销售量每件支出0.9元,水电房租费每日102元,若剩下的每天总纯利润要达到5100元,则每件涨价应为多少?
17.芯片行业是制约我国工业发展的主要技术之一.经过大量科研、技术人员艰苦攻关,我国芯片有了新突破.某芯片实现国产化后,芯片价格大幅下降.原来每片芯片的单价为元,准备进行两次降价,如果每次降价的百分率都为,经过两次降价后的价格为(元).
(1)求与之间的函数关系式;
(2)如果该芯片经过两次降价后每片芯片单价为元,求每次降价的百分率.
18.某种产品现在的年产量是,计划今后两年增加产量.如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示?
19.某商场第1年销售计算机5000台,如果每年的销售量比上一年增加相同的百分率x,写出第3年的销售量y关于每年增加的百分率x的函数解析式.
20.为积极响应国家“旧房改造”工程,该市推出《加快推进旧房改造工作的实施方案》推进新型城镇化建设,改善民生,优化城市建设.
(1)根据方案该市的旧房改造户数从2020年底的3万户增长到2022年底的4.32万户,求该市这两年旧房改造户数的平均年增长率;
(2)该市计划对某小区进行旧房改造,如果计划改造300户,计划投入改造费用平均20000元/户,且计划改造的户数每增加1户,投入改造费平均减少50元/户,求旧房改造申报的最高投入费用是多少元?
21.某公司的生产利润原来是万元,经过连续两年的增长达到了万元,如果每年增长率都是,写出利润与增长的百分率之间的函数解析式,它是什么函数?
22.某工厂前年的生产总值为10万元,去年比前年的年增长率为x,预计今年比去年的年增长率仍为x,今年的总产值为y万元.
(1)求y关于x的函数关系式.
(2)当x=20%时,今年的总产值为多少?
(3)在(2)的条件下,前年、去年和今年三年的总产值为多少万元?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【分析】根据题意,分别求出相应的函数解析式,进行判断即可;
【详解】解:①由题意,得:,故①是一次函数;
②由题意,得:,故②是二次函数;
③由题意,得:,故①是反比例函数;
故选B.
【点睛】本题考查列函数关系式.解题的关键是正确的列出函数关系式.
2.C
【分析】设的长为,矩形的面积为,则的长为,根据矩形的面积公式列二次函数解析式,再分别根据的长不能超过,二次函数的最值,解一元二次方程求解即可.
【详解】设的长为,矩形的面积为,则的长为,由题意得
,
其中,即,
①的长不可以为,原说法错误;
③菜园面积的最大值为,原说法正确;
②当时,解得或,
∴的长有两个不同的值满足菜园面积为,说法正确;
综上,正确结论的个数是2个,
故选:C.
【点睛】本题考查了二次函数的应用,解一元二次方程,准确理解题意,列出二次函数解析式是解题的关键.
3.C
【分析】设,分和,结合矩形的性质,表示三角形的面积,构造函数,结合图像,确定m,n的值计算即可.
【详解】解:设,
当时,,
根据图像,得当时,y取得最大值5,此时,
当时,,此时;
当时,P停止运动,
,
根据图像,当时,此时,
故,
故选:C.
【点睛】本题考查了数形结合思想,二次函数的最值,一次函数的性质,熟练掌握二次函数的最值,一次函数的性质是解题的关键.
4.C
【分析】如图,点D是点B关于直线的对称点,连接交于点P,则此时y取得最小值,即,即可求解.
【详解】解:如图,点D是点B关于直线的对称点,连接交于点P,
根据点的对称性,,则为最小,
故,
设正方形的边长为a,则,
在中,由勾股定理得:,
即,
解得:(负值已舍去),
故选:C.
【点睛】本题考查的是动点图象问题,涉及到二次函数、解直角三角形,正方形的性质,利用勾股定理求线段长是解题的关键.
5.C
【分析】根据条件易有点坐标为,点的坐标为,点的横坐标为4,将点和代入抛物线表达式可解的和的值,然后令计算点的纵坐标即为距离.
【详解】解:由题意可得:点坐标为,点的坐标为,
将点和代入抛物线表达式可得,解得
∴,
令,可得.
故选:C.
【点睛】本题主要考查二次函数的实际应用,能够根据条件得到对应点的坐标,解出抛物线表达式是解题的关键,然后在将实际问题转化为二次函数点的坐标问题.
6.C
【分析】利用建立的坐标系得到抛物线上点的坐标,然后通过待定系数法求出抛物线解析式,对照选项即可.
【详解】设解析式为,抛物线上点,,,带入抛物线解析式中得,解得,解析式为.
选项A中,,故选项A错误;
选项B中,解析式为,故选项B错误;
选项C中,池塘水深最深处为点,水面,,所以水深最深处为点P到水面的距离为3.2米,故选项C正确;
选项D中,若池塘中水面的宽度减少为原来的一半,由抛物线关于轴对称可知,抛物线上点横坐标,带入解析式算得,即到水面距离为米,而最深处到水面的距离为3.2米,减少为原来的.故选项D错误.
故选C.
【点睛】本题考查二次函数的实际应用问题,计算较为复杂,在计算时需要理清楚实际数据在坐标系中对应的位置.能够正确计算和分析实际情况是解题的关键.
7.A
【分析】根据题意列方程组求出二次函数的解析式,再列方程即可得到结论.
【详解】解:由题意知:当时,;当时,代入中,
得,
解得:,
∴,
当每天利润为0元时,售价即为成本价.令,
解得:,
由题意可知38不符合条件,
∴,
∴这种口罩的成本价是10元/个;
故选:A.
【点睛】本题考查了二次函数的应用,一元二次方程的应用,正确的理解题意是解题的关键.
8.D
【分析】根据球弹起后又回到地面时,得到,解方程即可得到答案.
【详解】解:球弹起后又回到地面时,即,
解得(不合题意,舍去),,
∴球弹起后又回到地面所花的时间(秒)是2,
故选:D
【点睛】此题考查了求二次函数自变量的值,读懂题意,得到方程是解题的关键.
9.C
【分析】由可得其对称轴为:,当时,,即有,解方程即可求解.
【详解】由可得其对称轴为:,
根据,
可知:当时,,
即有:,
解得:,
故选:C.
【点睛】本题考查了二次函数的图象与性质以及二次函数的应用等知识,明确题意,得出当时,,是解答本题的关键.
10.B
【分析】利用4月份该厂家口罩产量月份该厂家口罩产量从2月份到4月份该厂家口罩产量的平均月增长率,即可得出关于x的一元二次方程,此题得解.
【详解】解:根据题意得,
故选:B.
【点睛】本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
11.
【分析】阴影部分的长方形的的长为,宽为,然后根据长方形的面积公式即可求解.
【详解】阴影部分的长方形的的长为,宽为,
所以面积.
【点睛】本题考查了利用长方形的面积公式列出函数关系式,其中根据题意,找到所求量的等量关系是解决问题的关键.
12.
【分析】由②知,最大为5,此时点D与点A重合,,过点E作,交延长线于G,根据等腰三角形的性质及三角形等面积法得出,过点B作,交延长线于H,则,再由全等三角形的判定和性质得出,即可求解三角形面积.
【详解】解:由②知,最大为5,此时点D与点A重合,,
∵是等腰直角三角形,
∴,
过点E作,交延长线于G,
∴,
解得,
∴
过点B作,交延长线于H,则,
∵
∴,
∵,
∴,
∴,
∴
故答案为:.
【点睛】此题考查了动点问题与函数图象的结合,二次函数的图象和性质,全等三角形的判定和性质,综合掌握各知识点是解题的关键.
13.
【分析】设抛物线解析式为,根据题意可得,抛物线与x轴两交点坐标分别为、,代入即可求出.
【详解】解:设抛物线解析式为,
由题意可知:,抛物线与x轴两交点坐标分别为、,
把、,代入得:,
解得:,
∴抛物线解析式为,
故答案为:.
【点睛】本题考查了求抛物线解析式,正确设出解析式和确定点的坐标是解题关键.
14.
【分析】根据利润=每件利润×销量求解.
【详解】解:由题意得,
故答案为:.
【点睛】本题考查二次函数的应用,解题关键是根据题意列出函数解析式.
15.y=10(1+x)2
【分析】利用该厂九月份的产值=该厂七月份的产值×(1+增长率)2,即可得出结论.
【详解】解:∵该厂七月份的产值是10万元,且第三季度每个月产值的增长率相同,均为x,
∴该厂八月份的产值是10(1+x)万元,九月份的产值是10(1+x)2万元,
∴y=10(1+x)2.
故答案为:y=10(1+x)2.
【点睛】本题考查了由根据实际问题列二次函数关系式,根据各数量之间的关系,正确列出二次函数关系式是解题的关键.
16.(1)
(2)①每件应张价5元;②每件涨价应为8元
【分析】(1)设第二、三天的日平均增长率为x,利用第三天的销售量=第一天的销售量,即可得出关于x的一元二次方程,解之取其正值即可得出结论;
(2)①设每件应张价y元,则每件盈利(毛利润)为元,销售数量为件,根据每件盈利(毛利润)×销售数量=每天总毛利润列方程求解即可;
②设每件涨价应为z元,则每天总毛利润为元,每天总纯利润为元,根据每天总纯利润要达到5100元,列方程求解即可.
【详解】(1)解: 设第二、三天的日平均增长率为x,根据题意,得
,
解得: , (不符合题意,舍去),
∴,
答: 第二、三天的日平均增长率为10%.
(2)解:①设每件应张价y元,根据题意,得
,
解得:,,
∵要使顾客得到实惠,
∴,
答:每件应张价5元;
②设每件涨价应为z元,根据题意,得
,
解得:,
∴,
答:每件涨价应为8元.
【点睛】本题考查一元二次方程的应用,理解题意,设恰当未知数,找出等量关系,列出方程是解题的关键.
17.(1)
(2)
【分析】(1)利用经过两次降价后的价格原价每次降价的百分率,即可找出与之间了函数关系式;
(2)根据该芯片经过两次降价后每块芯片单价为元,即可得出关于的一元二次方程,解之取其符合题意的值即可得出结论.
【详解】(1)∵每次降价的百分率都为,经过两次降价后的价格为(元)
∴依题意得:,
∴与之间的函数关系式为;
(2)依题意得:,
解得:,(不符合题意,舍去),
∴每次降价的百分率为20%.
【点睛】本题考查了一元二次方程的应用以及二次函数关系式,解题的关键是:(1)根据各数量之间的关系,找出y关于x的函数关系式;(2)找准等量关系,正确列出一元二次方程.
18.,y是x的函数
【分析】根据题意可得一年后的产量是,再经过一年后的产量是,由此求解即可.
【详解】解:这种产品的原产量是,一年后的产量是,再经过一年后的产量是,即两年后的产量,
即①
①式表示了两年后的产量y与计划增产的倍数x之间的关系,对于x的每一个值,y都有一个对应值,即y是x的函数.
【电锯】本题考查了函数关系式,利用增长问题获得函数解析式是解题关键,注意增加x倍是原来的(x+1)倍.
19.y=5000x2+10000x+5000.
【分析】根据增长率第2年的销量=第1年的销量+增加百分率x×第1年的销量=(1+x)×第1年的销量,第3年的销售量y=第2年的销量+增加百分率x×第2年的销量=(1+x)×第2年的销量=(1+x)2×第1年的销量即可.
【详解】解:由题意可知y=500(1+x)2=5000x2+10000x+5000,
∴y=5000x2+10000x+5000.
【点睛】本题考查增长率问题,利用增长率求函数解析式,掌握增长率的公式是解题关键.
20.(1)20%;(2)6125000(元)
【分析】(1)设平均增长率为x,根据题意列式求解即可;
(2)设多改造y户,最高投入费用为w元,根据题意列式,然后根据二次函数的性质即可求出最大值.
【详解】解:(1)设平均增长率为x,则x>0,
由题意得:,
解得:x=0.2或x=-2.2(舍),
答:该市这两年旧房改造户数的平均年增长率为20%;
(2)设多改造a户,最高投入费用为w元,
由题意得:,
∵a=-50,抛物线开口向下,
∴当a-50=0,即a=50时,w最大,此时w=612500元,
答:旧房改造申报的最高投入费用为612500元.
【点睛】本题考查二次函数的实际应用,解题的关键是正确读懂题意列出式子,然后根据二次函数的性质进行求解.
21.见解析.
【分析】根据增长率的问题,基数是a元,增长次数2次,结果为y,根据增长率的公式表示函数关系式.
【详解】依题意,得:,
此函数是二次函数.
【点睛】此题主要考查了根据实际问题列二次函数关系式,在表示增长率问题时,要明确基数,增长次数,最后的结果.
22.(1);(2)万元;(3)万元.
【分析】(1)根据题意列式为y=10×(1+x)×(1+x)= 10(1+x) ;(2)把x的值代入(1)求解即可;(3)代入求解即可.
【详解】(1)根据题意列式为y=10×(1+x)×(1+x)=10(1+x) ;
(2)当x=20%时,今年的总产值=10(1+20%) =14.4万元;
(3) 依题意,得前年,去年和今年三年的总产值为:10+10(1+20%)+ 10(1+x) =36.4(万元).
【点睛】本题考查了二次函数的应用,解题的关键是将实际问题转化为二次函数求解.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
