1.5.1 乘方同步练习题(含解析)
文档属性
| 名称 | 1.5.1 乘方同步练习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 547.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-05 09:03:04 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
七年级数学上册 第一章 1.5.1 乘方 同步练习题
一、单选题
1.比较与,下列说法正确的是( )
A.它们的底数相同,指数也相同 B.它们所表示的意义相同,但运算结果不相同
C.它们底数相同,但指数不相同 D.虽然他们底数不同,但是运算结果相同
2.2023 我们来了,则的结果是( )
A.1 B. C. D.2022
3.如果,那么等于( )
A.-2 B.2 C. D.4
4.如果实数、,满足,那么的值等于( )
A. B. C. D.4
5.若,则称是以10为底的对数.记作:.例如:,则;,则.对数运算满足:当,时,,例如:,则的值为( )
A.5 B.2 C.1 D.0
6.下列四个算式:①②③,其中正确的有( )
A.0个 B.1个 C.2个 D.3个
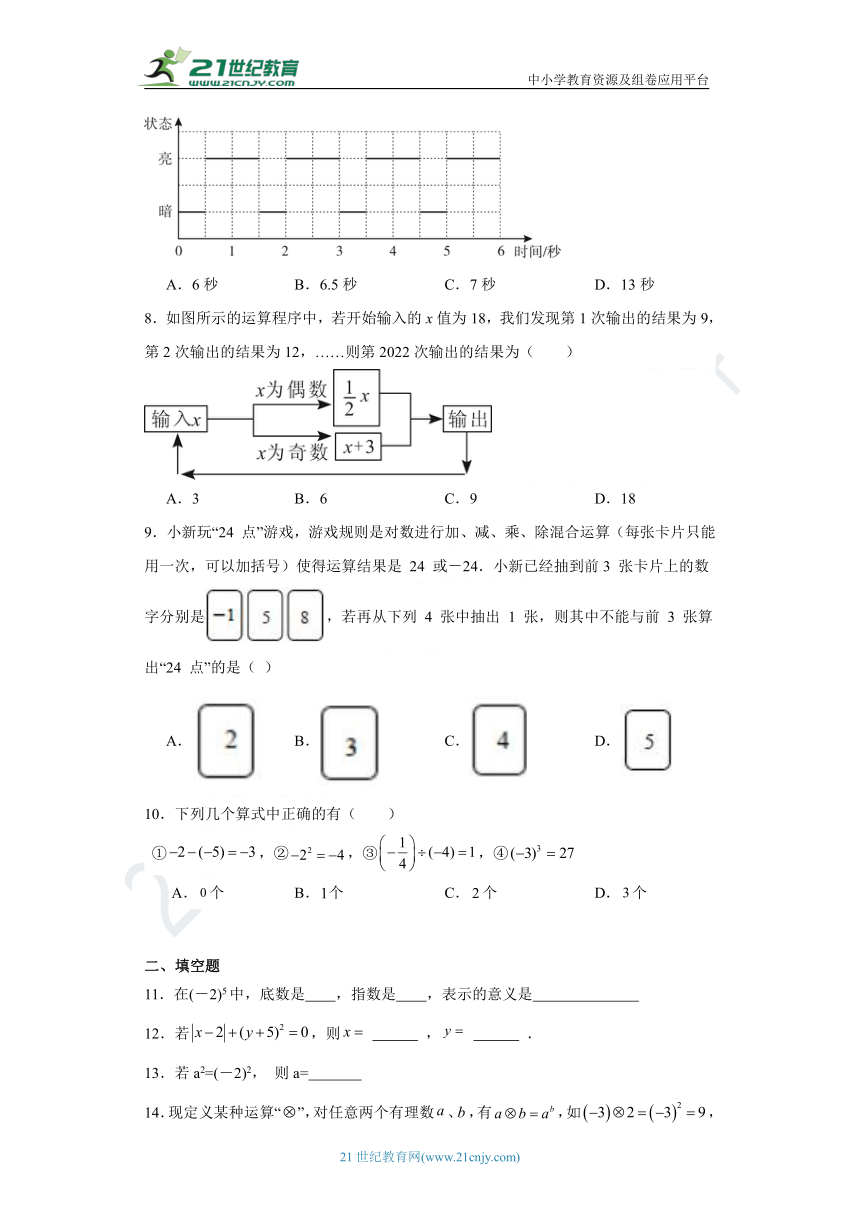
7.按《航空障碍灯(MH/T6012-1999)》的要求,为保障飞机夜间飞行的安全,在高度为45米至105米的建筑上必须安装中光强航空障碍灯(Aviation Obstruction light).中光强航空障碍灯是以规律性的固定模式闪光.下图是某一种中光强航空障碍灯的闪光模式,灯的亮暗呈规律性交替变化,那么在一个连续的10秒内,该航空障碍灯处于亮的状态时间总和最长可达( )
A.6秒 B.6.5秒 C.7秒 D.13秒
8.如图所示的运算程序中,若开始输入的x值为18,我们发现第1次输出的结果为9,第2次输出的结果为12,……则第2022次输出的结果为( )
A.3 B.6 C.9 D.18
9.小新玩“24 点”游戏,游戏规则是对数进行加、减、乘、除混合运算(每张卡片只能用一次,可以加括号)使得运算结果是 24 或-24.小新已经抽到前3 张卡片上的数字分别是,若再从下列 4 张中抽出 1 张,则其中不能与前 3 张算出“24 点”的是( )
A. B. C. D.
10.下列几个算式中正确的有( )
①,②,③,④
A.个 B.个 C.个 D.个
二、填空题
11.在(-2)5中,底数是 ,指数是 ,表示的意义是
12.若,则 , .
13.若a2=(-2)2, 则a=
14.现定义某种运算“”,对任意两个有理数、,有,如,计算: .
15.“人间四月芳菲尽,山寺桃花始盛开”.诗词反映了深山海拔高、气温低、花开晚的自然现象.研究表明:高山上的温度随海拔的升高而降低,一般是海拔升高100米,气温约下降0.6℃.已知位于山西省的恒山海拔为2016.1米,若山脚的气温是10℃,则此时山顶的气温约为 ℃.(结果保留整数)
三、解答题
16.阅读以下材料,完成下列问题.
(1)我们已经学过了乘方运算,我们知道表示2个-2相乘,即,那么表示 ,把写成乘方的形式表示为 ,此时底数是 .
(2)将(1)中两个底数同为-2的幂相乘,即,结果共有 个-2相乘,写成幂的形式为 ;
(3)若将(2)中算式中的底数都换为,则表示 ,计算结果为 .
若将(2)中算式中的指数换为正整数,则 ,请用一句话概括你发现的结论 ;
(4)利用上述结论,完成以下填空
若,则 , ;
若,,,写出的数量关系 .
17.类比有理数的乘方,我们定义“除方”运算,比如:可写作2③,(-3)÷(-3)÷(-3)÷(-3)写作(-3)④,一般地把n个a相除写作,读作“a的圈n次方”.
(1)直接写出计算结果:2③=_______; ③=_______.
(2)我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,那么除方运算如何转化为乘方运算呢?方法如下:
除方→→乘方的形式
仿照以上例子,把除方运算写乘方形式:=______,=_______.
(3)算一算:.
18.计算:
(1)
(2)
(3)
(4)已知一个多项式乘的积为,求这个多项式
19.有三个有理数x,y,z,若x=,且x与y互为相反数,y是z的倒数.
(1)当n为奇数时,你能求出x,y,z这三个数吗?当n为偶数时,你能求出x,y,z,这三个数吗?若能,请计算并写出结果;若不能,请说明理由.
(2)根据(1)的结果计算:xy﹣yn﹣(y﹣z)2019的值.
20.“疫情无情人有情”,在抗击新冠病毒疫情期间,一志愿小组某天早晨从A地出发沿南北方向运送抗疫物资,晚上最后到达B地,约定向北为正方向,当天志愿小组行驶记录如下(单位:千米):
.
(1)试问B地在A地的哪个方向,它们相距多少千米?
(2)若汽车行驶每千米耗油0.08升,则志愿小组该天共耗油多少升?
21.出租车司机小王某天下午营运全是在南北走向的公路上进行的.如果向南记作“+”,向北记作“”,他这天下午行车情况如下:(单位:千米)
,,8,,,
(1)若出租车每公里耗油升,求小王回到出发地共耗油多少升?
(2)若规定每趟车的起步价是10元,且每趟车3千米以内(含3千米)只收起步价;若超过3千米,除收起步价外,超过的每千米(不足1千米按1千米计算)还需收4元钱,小王今天是收入是多少元?
22.计算题:
(1)
(2)
(3)
(4)
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.D
【分析】根据有理数幂的概念解答即可.
【详解】解:的底数是3,指数是3,表示3个3的乘积的相反数,运算结果为,
的底数是,指数是3,表示3个的乘积,运算结果为,
故它们的底数不同,指数相同,所表示的意义不同,但运算结果相同,
所以,选项A、B、C说法错误,不符合题意,选项D说法正确,符合题意,
故选:D.
【点睛】本题考查有理数的乘方,解答的关键是熟练掌握有理数幂的概念:表示n个a的乘积,a为底数,n为指数.
2.B
【分析】根据乘方的意义即可求解.
【详解】解:.
故选:B.
【点睛】本题考查了乘方的运算法则,解题的关键在于熟练掌握乘方的运算法则.正数的任何次幂都是正数,负数的偶次幂是正数,负数的奇次幂是负数,0的任何正整数次幂都等于0.
3.C
【分析】根据,可知,据此解答选择即可.
【详解】因为,所以,所以,故答案选C.
【点睛】本题考查的是有理数的乘方和乘法法则,根据有理数乘方的意义计算出,是解题的关键.
4.D
【分析】根据非负数的和为零,可得每个非负数同时为零,可得、的值,根据负数的偶数次幂是正数,可得答案.
【详解】解:由,得
,.
解得,.
那么的值等于4,
故选:D.
【点睛】本题考查了非负数的性质,解题的关键是利用非负数的和为零得出每个非负数同时为零.
5.C
【分析】通过阅读自定义运算规则:,再得到 再通过提取公因式后逐步进行运算即可得到答案.
【详解】解: ,
故选C
【点睛】本题考查的是自定义运算,理解题意,弄懂自定义的运算法则是解本题的关键.
6.B
【分析】根据有理数相关运算的法则逐项判断.
【详解】解:,故①错误;
,故②错误;
,故③正确;
,故④错误,
∴正确的有③,共1个,
故选:B.
【点睛】本题考查有理数的运算,解题的关键是掌握有理数相关运算的法则.
7.C
【分析】根据题意可得当该航空障碍灯处于亮的状态的时间总和最长时的灯的亮暗呈规律性交替变化规律,故可求解.
【详解】解:根据题意,当该航空障碍灯处于亮的状态的时间总和最长时,灯的亮暗呈规律性交替变化为:亮1秒,暗0.5秒,亮1秒,暗0.5秒,亮1秒,暗0.5秒,亮1秒,暗0.5秒,亮1秒,暗0.5秒,亮1秒,暗0.5秒,亮1秒,
故在这10秒中,航空障碍灯处于亮的状态的时间总和为7秒,
故选C.
【点睛】本题考查了有理数的运算,正确理解图示是解题的关键.
8.A
【分析】计算出第3次,第4次,第5次,…,输出的结果,根据计算结果得出规律即可求解.
【详解】解:输入18,则第1次输出的是:;
第2次输出的数是;
第3次输出的数是:;
第4次输出的数是:;
第5次输出的数是:;
则第6次输出:3;
如此循环,从第3次开始,偶数次输出的是3,奇数次输出的是6.
故第2022次输出3.
故选:A.
【点睛】本题考查在程序流程图中有理数的计算,解题的关键是发现其中的规律,利用规律进行解答.
9.D
【分析】利用运算符号将四个数字连接,使其结果为24或-24,即可得出答案.
【详解】A:(5-2)×8×(-1)=-24,故A错误;
B:(8-3)×5+(-1)=24,故B错误;
C:(8-4)×[5-(-1)]=24,故C错误;
D:无法组成24点,故D正确;
故答案选择:D.
【点睛】本题考查的是有理数的混合运算,需要熟练掌握有理数的运算法则.
10.B
【分析】根据有理数的四则混合运算法则即可求解.
【详解】解:①,故①错误;
②,故②正确;
③,故③错误;
④,故④错误.
综上所述,正确的有②,
故选:.
【点睛】本题主要考查有理数的混合运算,掌握有理数的中去括号法则,乘方运算,有理数除法法则是解题的关键.
11. -2 5 5个-2相乘
【分析】根据乘方的意义可得答案.
【详解】解:在(-2)5中,底数是-2,指数是5,表示的意义是5个-2相乘,
故答案为: 2,5,5个 2相乘.
【点睛】本题考查了乘方的意义.熟知底数是相同的因数,指数是相同因数的个数,幂表示相同因数的积是解题的关键.
12. 2
【分析】根据非负数的性质列式即可求得、的值.
【详解】解:根据题意得,,,
解得,,
故答案为:2,.
【点睛】本题考查非负数的性质,两个非负数的和为0,则它们分别为0.
13.或
【分析】根据乘方的意义计算即可得到结果.
【详解】∵
∴或
故填:或.
【点睛】本题考查了有理数的乘方,熟练掌握乘方的意义是解本题的关键.
14.1
【分析】理解“”,先算括号内的,再算括号外的.
【详解】
故答案为:1.
【点睛】此题是新定义运算题型,考查有理数的乘方.关键要理解新定义的运算含义和乘方的意义.
15.-2
【分析】先表示出山顶的气温的代数式,然后再计算即可.
【详解】解:根据题意得:
山顶的气温为:(℃).
故答案为:-2.
【点睛】本题主要考查了有理数的混合运算,根据“海拔每升高100米,气温就下降0.6℃”正确列式是解题的关键.
16.(1)3个-2相乘,即;;;;(2)5;;(3)5个相乘,即;;;同底数幂相乘,底数不变,指数相加;(4);25;
【分析】(1)利用乘法和乘方的意义,得到结果;
(2)利用同底数幂的乘法公式,进行计算.
(3)利用同底数幂的乘法公式,进行计算,并得到结论.
(4)利用同底数幂的乘法公式,进行计算.
【详解】(1)表示3个-2相乘,,把写成乘方的形式表示为,此时底数是.
(2)将(1)中两个底数同为-2的幂相乘,即,结果共有5个-2相乘,写成幂的形式为;
(3)若将(2)中算式中的底数都换为,则表示5个相乘,即,计算结果为.
若将(2)中算式中的指数换为正整数,则,请用一句话概括你发现的结论同底数幂相乘,底数不变,指数相加;
(4)利用上述结论,完成以下填空
若,则,25;
若,,,写出的数量关系:
即:.
【点睛】本题考查了同底数幂的乘法公式的推导和应用同底数幂的乘法公式的计算.掌握公式是关键.
17.(1),
(2),
(3)
【分析】(1)根据新定义的运算计算即可;
(2)根据题干中的运算方法求解即可;
(3)利用(1)(2)中的方法代入化简,然后计算即可.
【详解】(1)解:,
,
故答案为:,;
(2),
,
故答案为:,;
(3)
.
【点睛】题目主要考查含乘方的有理数的混合运算,理解题干中新定义的运算方法是解题关键.
18.(1)-4;(2);(3)ab;(4)
【详解】试题分析:(1)直接利用积的乘方运算法则将原式变形进而求出答案.
(2)先运用单项式乘以多项式和完全平方公式把括号去掉,然后再合并同类项即可得解;
(3)先去小括号,再合并同类项,再根据多项式除以单项式的法则计算即可.
(4)根据题意列出算式,再根据多项式除以单项式法则求出即可.
试题解析:(1)(0.25)2016×(-4)2017=(0.25×4)2016×(-4)=-4.
(2)2x(2x-y)-(2x-y)2=4x2-2xy-4x2+4xy-y2=2xy- y2;
(3)
=(a2b2-1-2a2b2+1)÷(-ab)
=(-a2b2) ÷(-ab)
=ab
(4)由题意得:(-8a4+10a3-4a2)÷(-2a2)
=4a2-5a+2,
即这个多项式为4a2-5a+2.
19.(1)n为奇数时,x=﹣1,y=1,z=1,n为偶数时,不能求出这3个数;(2)-2.
【分析】(1)根据n为奇数,确定出x的值,进而利用相反数,倒数的定义以及乘方的意义求出y,z的值;
(2)将x,y,z的值代入原式计算即可得到结果.
【详解】解:(1)当n为奇数时,x==﹣1,
x与y互为相反数,所以y=1,
y是z的倒数,所以z=1,
当n为偶数时,分母为0没有意义,则不能求出这3个数.
(2)当x=﹣1,y=1,z=1时,
原式=
=﹣1﹣1﹣0
=﹣2.
【点睛】本题考查求相反数和倒数,有理数的乘方,熟练掌握有理数的基本概念与乘方的计算是解题的关键.
20.(1)B地在A地的南方,它们相距32千米
(2)天共耗油8.64升
【分析】(1)先根据有理数的加减混合运算,把当天的行驶记录相加;然后根据正、负数的意义,判断出B地在A地的哪个方向,它们相距多少千米即可;
(2)先求出当天行驶记录的绝对值的和,再用汽车汽车行驶的路程乘以行驶每千米耗油量,求出该天共耗油多少升即可.
【详解】(1)
答:B地在A地的南方,它们相距32千米.
(2)(升)
答:汽车行驶每千米耗油0.08升,则志愿小组该天共耗油8.64升.
【点睛】此题考查正数和负数,以及有理数混合运算的应用,此题的关键是读懂题意,理清正数和负数的意义.
21.(1)升
(2)108元
【分析】(1)先求出最后一趟返回时的路程,再将行程里程相加,求出总路程,再根据出租车每公里耗油升,可得答案;
(2)根据行车记录和收费方法列出算式,计算即可得解.
【详解】(1)解:,
千米,
升,
小王回到出发地共耗油升.
(2)根据出租车收费标准,可知小王今天的收入是:
(元),
小王今天的收入是100元.
【点睛】本题考查有理数的加法运算,有理数的乘法运算,解题的关键是掌握有理数的运算法则.
22.(1)
(2)0
(3)0
(4)
【分析】(1)先化简符号,再算加减法;
(2)先算乘方和括号内的,再算乘法,最后计算加减法;
(3)利用乘法分配律展开计算;
(4)先算乘方,再算乘除,最后计算加减.
【详解】(1)解:
;
(2)
;
(3)
;
(4)
.
【点睛】此题考查了有理数的混合运算,有理数的混合运算首先弄清运算顺序,先乘方,再乘除,最后算加减,有括号先算括号里边的,同级运算从左到右依次进行计算,然后利用各种运算法则计算,有时利用运算律来简化运算.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
七年级数学上册 第一章 1.5.1 乘方 同步练习题
一、单选题
1.比较与,下列说法正确的是( )
A.它们的底数相同,指数也相同 B.它们所表示的意义相同,但运算结果不相同
C.它们底数相同,但指数不相同 D.虽然他们底数不同,但是运算结果相同
2.2023 我们来了,则的结果是( )
A.1 B. C. D.2022
3.如果,那么等于( )
A.-2 B.2 C. D.4
4.如果实数、,满足,那么的值等于( )
A. B. C. D.4
5.若,则称是以10为底的对数.记作:.例如:,则;,则.对数运算满足:当,时,,例如:,则的值为( )
A.5 B.2 C.1 D.0
6.下列四个算式:①②③,其中正确的有( )
A.0个 B.1个 C.2个 D.3个
7.按《航空障碍灯(MH/T6012-1999)》的要求,为保障飞机夜间飞行的安全,在高度为45米至105米的建筑上必须安装中光强航空障碍灯(Aviation Obstruction light).中光强航空障碍灯是以规律性的固定模式闪光.下图是某一种中光强航空障碍灯的闪光模式,灯的亮暗呈规律性交替变化,那么在一个连续的10秒内,该航空障碍灯处于亮的状态时间总和最长可达( )
A.6秒 B.6.5秒 C.7秒 D.13秒
8.如图所示的运算程序中,若开始输入的x值为18,我们发现第1次输出的结果为9,第2次输出的结果为12,……则第2022次输出的结果为( )
A.3 B.6 C.9 D.18
9.小新玩“24 点”游戏,游戏规则是对数进行加、减、乘、除混合运算(每张卡片只能用一次,可以加括号)使得运算结果是 24 或-24.小新已经抽到前3 张卡片上的数字分别是,若再从下列 4 张中抽出 1 张,则其中不能与前 3 张算出“24 点”的是( )
A. B. C. D.
10.下列几个算式中正确的有( )
①,②,③,④
A.个 B.个 C.个 D.个
二、填空题
11.在(-2)5中,底数是 ,指数是 ,表示的意义是
12.若,则 , .
13.若a2=(-2)2, 则a=
14.现定义某种运算“”,对任意两个有理数、,有,如,计算: .
15.“人间四月芳菲尽,山寺桃花始盛开”.诗词反映了深山海拔高、气温低、花开晚的自然现象.研究表明:高山上的温度随海拔的升高而降低,一般是海拔升高100米,气温约下降0.6℃.已知位于山西省的恒山海拔为2016.1米,若山脚的气温是10℃,则此时山顶的气温约为 ℃.(结果保留整数)
三、解答题
16.阅读以下材料,完成下列问题.
(1)我们已经学过了乘方运算,我们知道表示2个-2相乘,即,那么表示 ,把写成乘方的形式表示为 ,此时底数是 .
(2)将(1)中两个底数同为-2的幂相乘,即,结果共有 个-2相乘,写成幂的形式为 ;
(3)若将(2)中算式中的底数都换为,则表示 ,计算结果为 .
若将(2)中算式中的指数换为正整数,则 ,请用一句话概括你发现的结论 ;
(4)利用上述结论,完成以下填空
若,则 , ;
若,,,写出的数量关系 .
17.类比有理数的乘方,我们定义“除方”运算,比如:可写作2③,(-3)÷(-3)÷(-3)÷(-3)写作(-3)④,一般地把n个a相除写作,读作“a的圈n次方”.
(1)直接写出计算结果:2③=_______; ③=_______.
(2)我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,那么除方运算如何转化为乘方运算呢?方法如下:
除方→→乘方的形式
仿照以上例子,把除方运算写乘方形式:=______,=_______.
(3)算一算:.
18.计算:
(1)
(2)
(3)
(4)已知一个多项式乘的积为,求这个多项式
19.有三个有理数x,y,z,若x=,且x与y互为相反数,y是z的倒数.
(1)当n为奇数时,你能求出x,y,z这三个数吗?当n为偶数时,你能求出x,y,z,这三个数吗?若能,请计算并写出结果;若不能,请说明理由.
(2)根据(1)的结果计算:xy﹣yn﹣(y﹣z)2019的值.
20.“疫情无情人有情”,在抗击新冠病毒疫情期间,一志愿小组某天早晨从A地出发沿南北方向运送抗疫物资,晚上最后到达B地,约定向北为正方向,当天志愿小组行驶记录如下(单位:千米):
.
(1)试问B地在A地的哪个方向,它们相距多少千米?
(2)若汽车行驶每千米耗油0.08升,则志愿小组该天共耗油多少升?
21.出租车司机小王某天下午营运全是在南北走向的公路上进行的.如果向南记作“+”,向北记作“”,他这天下午行车情况如下:(单位:千米)
,,8,,,
(1)若出租车每公里耗油升,求小王回到出发地共耗油多少升?
(2)若规定每趟车的起步价是10元,且每趟车3千米以内(含3千米)只收起步价;若超过3千米,除收起步价外,超过的每千米(不足1千米按1千米计算)还需收4元钱,小王今天是收入是多少元?
22.计算题:
(1)
(2)
(3)
(4)
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.D
【分析】根据有理数幂的概念解答即可.
【详解】解:的底数是3,指数是3,表示3个3的乘积的相反数,运算结果为,
的底数是,指数是3,表示3个的乘积,运算结果为,
故它们的底数不同,指数相同,所表示的意义不同,但运算结果相同,
所以,选项A、B、C说法错误,不符合题意,选项D说法正确,符合题意,
故选:D.
【点睛】本题考查有理数的乘方,解答的关键是熟练掌握有理数幂的概念:表示n个a的乘积,a为底数,n为指数.
2.B
【分析】根据乘方的意义即可求解.
【详解】解:.
故选:B.
【点睛】本题考查了乘方的运算法则,解题的关键在于熟练掌握乘方的运算法则.正数的任何次幂都是正数,负数的偶次幂是正数,负数的奇次幂是负数,0的任何正整数次幂都等于0.
3.C
【分析】根据,可知,据此解答选择即可.
【详解】因为,所以,所以,故答案选C.
【点睛】本题考查的是有理数的乘方和乘法法则,根据有理数乘方的意义计算出,是解题的关键.
4.D
【分析】根据非负数的和为零,可得每个非负数同时为零,可得、的值,根据负数的偶数次幂是正数,可得答案.
【详解】解:由,得
,.
解得,.
那么的值等于4,
故选:D.
【点睛】本题考查了非负数的性质,解题的关键是利用非负数的和为零得出每个非负数同时为零.
5.C
【分析】通过阅读自定义运算规则:,再得到 再通过提取公因式后逐步进行运算即可得到答案.
【详解】解: ,
故选C
【点睛】本题考查的是自定义运算,理解题意,弄懂自定义的运算法则是解本题的关键.
6.B
【分析】根据有理数相关运算的法则逐项判断.
【详解】解:,故①错误;
,故②错误;
,故③正确;
,故④错误,
∴正确的有③,共1个,
故选:B.
【点睛】本题考查有理数的运算,解题的关键是掌握有理数相关运算的法则.
7.C
【分析】根据题意可得当该航空障碍灯处于亮的状态的时间总和最长时的灯的亮暗呈规律性交替变化规律,故可求解.
【详解】解:根据题意,当该航空障碍灯处于亮的状态的时间总和最长时,灯的亮暗呈规律性交替变化为:亮1秒,暗0.5秒,亮1秒,暗0.5秒,亮1秒,暗0.5秒,亮1秒,暗0.5秒,亮1秒,暗0.5秒,亮1秒,暗0.5秒,亮1秒,
故在这10秒中,航空障碍灯处于亮的状态的时间总和为7秒,
故选C.
【点睛】本题考查了有理数的运算,正确理解图示是解题的关键.
8.A
【分析】计算出第3次,第4次,第5次,…,输出的结果,根据计算结果得出规律即可求解.
【详解】解:输入18,则第1次输出的是:;
第2次输出的数是;
第3次输出的数是:;
第4次输出的数是:;
第5次输出的数是:;
则第6次输出:3;
如此循环,从第3次开始,偶数次输出的是3,奇数次输出的是6.
故第2022次输出3.
故选:A.
【点睛】本题考查在程序流程图中有理数的计算,解题的关键是发现其中的规律,利用规律进行解答.
9.D
【分析】利用运算符号将四个数字连接,使其结果为24或-24,即可得出答案.
【详解】A:(5-2)×8×(-1)=-24,故A错误;
B:(8-3)×5+(-1)=24,故B错误;
C:(8-4)×[5-(-1)]=24,故C错误;
D:无法组成24点,故D正确;
故答案选择:D.
【点睛】本题考查的是有理数的混合运算,需要熟练掌握有理数的运算法则.
10.B
【分析】根据有理数的四则混合运算法则即可求解.
【详解】解:①,故①错误;
②,故②正确;
③,故③错误;
④,故④错误.
综上所述,正确的有②,
故选:.
【点睛】本题主要考查有理数的混合运算,掌握有理数的中去括号法则,乘方运算,有理数除法法则是解题的关键.
11. -2 5 5个-2相乘
【分析】根据乘方的意义可得答案.
【详解】解:在(-2)5中,底数是-2,指数是5,表示的意义是5个-2相乘,
故答案为: 2,5,5个 2相乘.
【点睛】本题考查了乘方的意义.熟知底数是相同的因数,指数是相同因数的个数,幂表示相同因数的积是解题的关键.
12. 2
【分析】根据非负数的性质列式即可求得、的值.
【详解】解:根据题意得,,,
解得,,
故答案为:2,.
【点睛】本题考查非负数的性质,两个非负数的和为0,则它们分别为0.
13.或
【分析】根据乘方的意义计算即可得到结果.
【详解】∵
∴或
故填:或.
【点睛】本题考查了有理数的乘方,熟练掌握乘方的意义是解本题的关键.
14.1
【分析】理解“”,先算括号内的,再算括号外的.
【详解】
故答案为:1.
【点睛】此题是新定义运算题型,考查有理数的乘方.关键要理解新定义的运算含义和乘方的意义.
15.-2
【分析】先表示出山顶的气温的代数式,然后再计算即可.
【详解】解:根据题意得:
山顶的气温为:(℃).
故答案为:-2.
【点睛】本题主要考查了有理数的混合运算,根据“海拔每升高100米,气温就下降0.6℃”正确列式是解题的关键.
16.(1)3个-2相乘,即;;;;(2)5;;(3)5个相乘,即;;;同底数幂相乘,底数不变,指数相加;(4);25;
【分析】(1)利用乘法和乘方的意义,得到结果;
(2)利用同底数幂的乘法公式,进行计算.
(3)利用同底数幂的乘法公式,进行计算,并得到结论.
(4)利用同底数幂的乘法公式,进行计算.
【详解】(1)表示3个-2相乘,,把写成乘方的形式表示为,此时底数是.
(2)将(1)中两个底数同为-2的幂相乘,即,结果共有5个-2相乘,写成幂的形式为;
(3)若将(2)中算式中的底数都换为,则表示5个相乘,即,计算结果为.
若将(2)中算式中的指数换为正整数,则,请用一句话概括你发现的结论同底数幂相乘,底数不变,指数相加;
(4)利用上述结论,完成以下填空
若,则,25;
若,,,写出的数量关系:
即:.
【点睛】本题考查了同底数幂的乘法公式的推导和应用同底数幂的乘法公式的计算.掌握公式是关键.
17.(1),
(2),
(3)
【分析】(1)根据新定义的运算计算即可;
(2)根据题干中的运算方法求解即可;
(3)利用(1)(2)中的方法代入化简,然后计算即可.
【详解】(1)解:,
,
故答案为:,;
(2),
,
故答案为:,;
(3)
.
【点睛】题目主要考查含乘方的有理数的混合运算,理解题干中新定义的运算方法是解题关键.
18.(1)-4;(2);(3)ab;(4)
【详解】试题分析:(1)直接利用积的乘方运算法则将原式变形进而求出答案.
(2)先运用单项式乘以多项式和完全平方公式把括号去掉,然后再合并同类项即可得解;
(3)先去小括号,再合并同类项,再根据多项式除以单项式的法则计算即可.
(4)根据题意列出算式,再根据多项式除以单项式法则求出即可.
试题解析:(1)(0.25)2016×(-4)2017=(0.25×4)2016×(-4)=-4.
(2)2x(2x-y)-(2x-y)2=4x2-2xy-4x2+4xy-y2=2xy- y2;
(3)
=(a2b2-1-2a2b2+1)÷(-ab)
=(-a2b2) ÷(-ab)
=ab
(4)由题意得:(-8a4+10a3-4a2)÷(-2a2)
=4a2-5a+2,
即这个多项式为4a2-5a+2.
19.(1)n为奇数时,x=﹣1,y=1,z=1,n为偶数时,不能求出这3个数;(2)-2.
【分析】(1)根据n为奇数,确定出x的值,进而利用相反数,倒数的定义以及乘方的意义求出y,z的值;
(2)将x,y,z的值代入原式计算即可得到结果.
【详解】解:(1)当n为奇数时,x==﹣1,
x与y互为相反数,所以y=1,
y是z的倒数,所以z=1,
当n为偶数时,分母为0没有意义,则不能求出这3个数.
(2)当x=﹣1,y=1,z=1时,
原式=
=﹣1﹣1﹣0
=﹣2.
【点睛】本题考查求相反数和倒数,有理数的乘方,熟练掌握有理数的基本概念与乘方的计算是解题的关键.
20.(1)B地在A地的南方,它们相距32千米
(2)天共耗油8.64升
【分析】(1)先根据有理数的加减混合运算,把当天的行驶记录相加;然后根据正、负数的意义,判断出B地在A地的哪个方向,它们相距多少千米即可;
(2)先求出当天行驶记录的绝对值的和,再用汽车汽车行驶的路程乘以行驶每千米耗油量,求出该天共耗油多少升即可.
【详解】(1)
答:B地在A地的南方,它们相距32千米.
(2)(升)
答:汽车行驶每千米耗油0.08升,则志愿小组该天共耗油8.64升.
【点睛】此题考查正数和负数,以及有理数混合运算的应用,此题的关键是读懂题意,理清正数和负数的意义.
21.(1)升
(2)108元
【分析】(1)先求出最后一趟返回时的路程,再将行程里程相加,求出总路程,再根据出租车每公里耗油升,可得答案;
(2)根据行车记录和收费方法列出算式,计算即可得解.
【详解】(1)解:,
千米,
升,
小王回到出发地共耗油升.
(2)根据出租车收费标准,可知小王今天的收入是:
(元),
小王今天的收入是100元.
【点睛】本题考查有理数的加法运算,有理数的乘法运算,解题的关键是掌握有理数的运算法则.
22.(1)
(2)0
(3)0
(4)
【分析】(1)先化简符号,再算加减法;
(2)先算乘方和括号内的,再算乘法,最后计算加减法;
(3)利用乘法分配律展开计算;
(4)先算乘方,再算乘除,最后计算加减.
【详解】(1)解:
;
(2)
;
(3)
;
(4)
.
【点睛】此题考查了有理数的混合运算,有理数的混合运算首先弄清运算顺序,先乘方,再乘除,最后算加减,有括号先算括号里边的,同级运算从左到右依次进行计算,然后利用各种运算法则计算,有时利用运算律来简化运算.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
