4.1.1 立体图形与平面图形同步练习题(含解析)
文档属性
| 名称 | 4.1.1 立体图形与平面图形同步练习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 771.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-05 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
七年级数学上册 第四章
4.1.1 立体图形与平面图形 同步练习题
一、单选题
1.下列立体图形中,是圆锥的是( )
A. B. C. D.
2.如图所示,每个小立方体的棱长为1,按如图所示的视线方向看,图1中共有1个1立方体,其中1个看得见,0个看不见;图2中共有8个立方体,其中7个看得见,1个看不见;图3中共有27个小立方体,其中19个看得见,8个看不见;…,则第11个图形中,其中看得见的小立方体个数是( )
A.271 B.272 C.331 D.332
3.下列几何中,属于棱柱的是( )
① ② ③ ④ ⑤ ⑥
A.①③ B.① C.①③⑥ D.①⑥
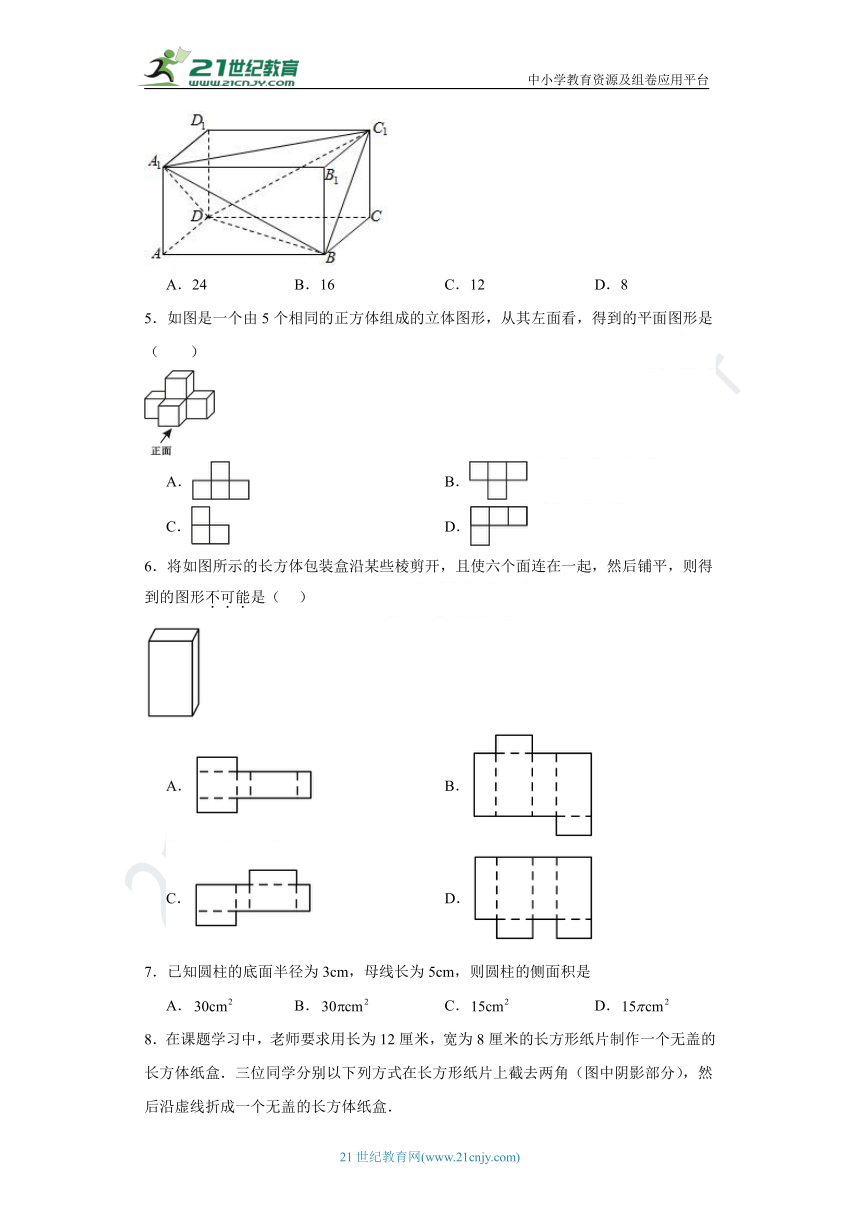
4.如图,在长方体ABCD﹣A1B1C1D1中,已知AB=4,AD=3,AA1=2.则三棱锥C1﹣A1DB的体积为( )
A.24 B.16 C.12 D.8
5.如图是一个由5个相同的正方体组成的立体图形,从其左面看,得到的平面图形是( )
A. B.
C. D.
6.将如图所示的长方体包装盒沿某些棱剪开,且使六个面连在一起,然后铺平,则得到的图形不可能是( )
A. B.
C. D.
7.已知圆柱的底面半径为3cm,母线长为5cm,则圆柱的侧面积是
A. B. C. D.
8.在课题学习中,老师要求用长为12厘米,宽为8厘米的长方形纸片制作一个无盖的长方体纸盒.三位同学分别以下列方式在长方形纸片上截去两角(图中阴影部分),然后沿虚线折成一个无盖的长方体纸盒.
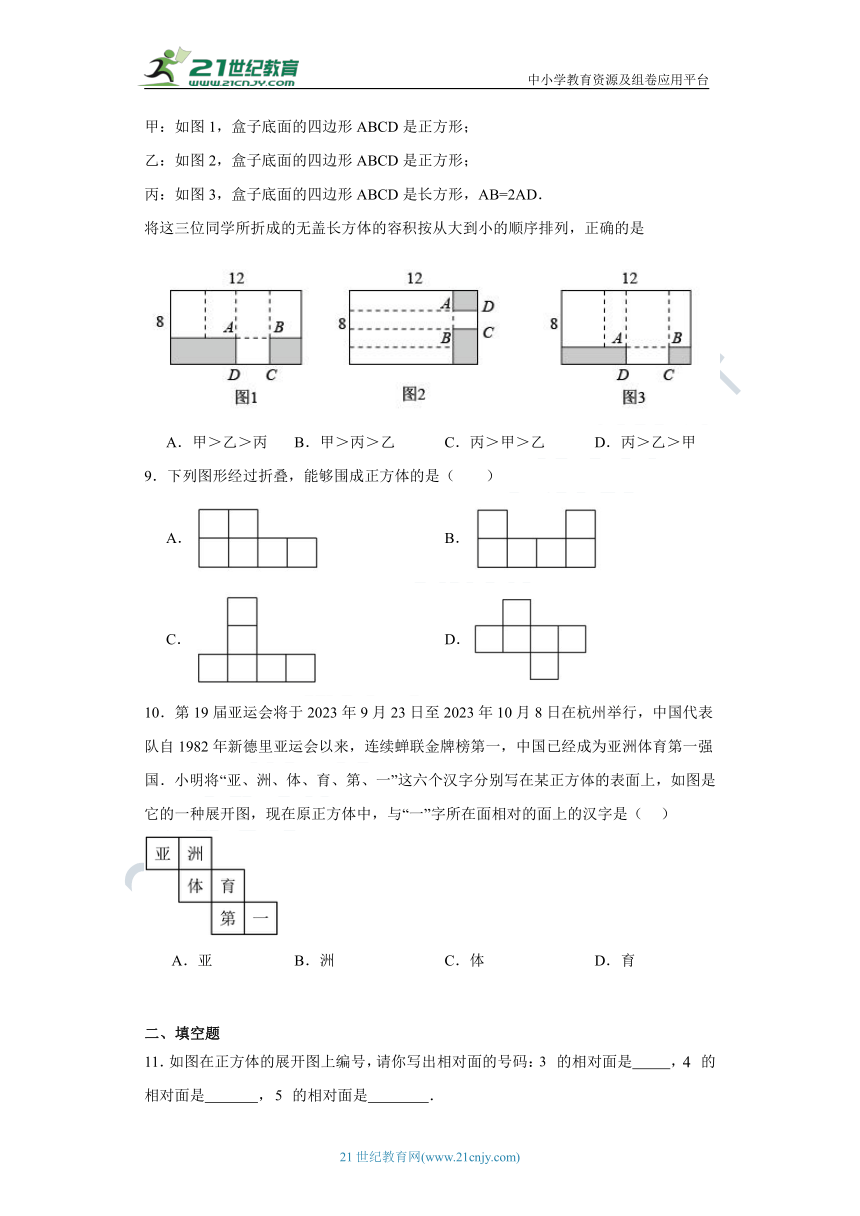
甲:如图1,盒子底面的四边形ABCD是正方形;
乙:如图2,盒子底面的四边形ABCD是正方形;
丙:如图3,盒子底面的四边形ABCD是长方形,AB=2AD.
将这三位同学所折成的无盖长方体的容积按从大到小的顺序排列,正确的是
A.甲>乙>丙 B.甲>丙>乙 C.丙>甲>乙 D.丙>乙>甲
9.下列图形经过折叠,能够围成正方体的是( )
A. B.
C. D.
10.第19届亚运会将于2023年9月23日至2023年10月8日在杭州举行,中国代表队自1982年新德里亚运会以来,连续蝉联金牌榜第一,中国已经成为亚洲体育第一强国.小明将“亚、洲、体、育、第、一”这六个汉字分别写在某正方体的表面上,如图是它的一种展开图,现在原正方体中,与“一”字所在面相对的面上的汉字是( )
A.亚 B.洲 C.体 D.育
二、填空题
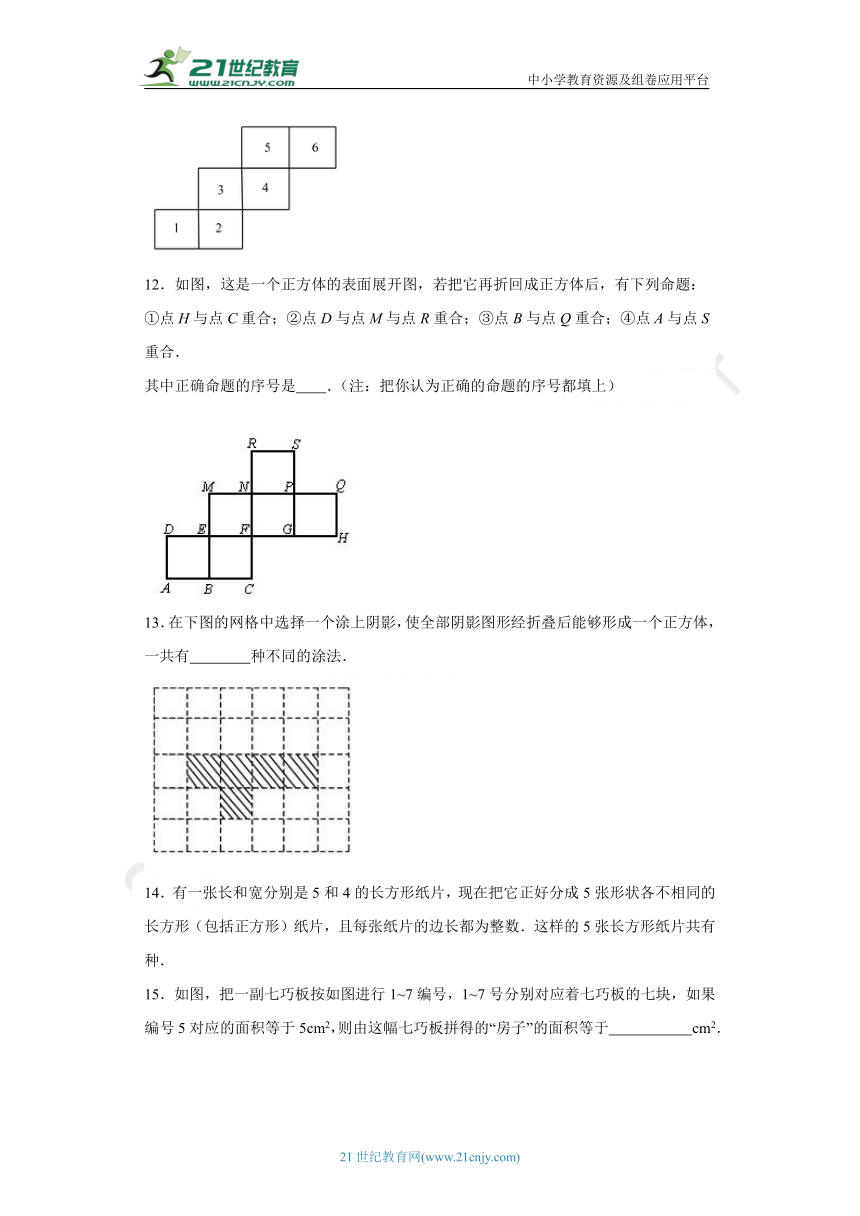
11.如图在正方体的展开图上编号,请你写出相对面的号码: 的相对面是 , 的相对面是 , 的相对面是 .
12.如图,这是一个正方体的表面展开图,若把它再折回成正方体后,有下列命题:
①点H与点C重合;②点D与点M与点R重合;③点B与点Q重合;④点A与点S重合.
其中正确命题的序号是 .(注:把你认为正确的命题的序号都填上)
13.在下图的网格中选择一个涂上阴影,使全部阴影图形经折叠后能够形成一个正方体,一共有 种不同的涂法.
14.有一张长和宽分别是5和4的长方形纸片,现在把它正好分成5张形状各不相同的长方形(包括正方形)纸片,且每张纸片的边长都为整数.这样的5张长方形纸片共有 种.
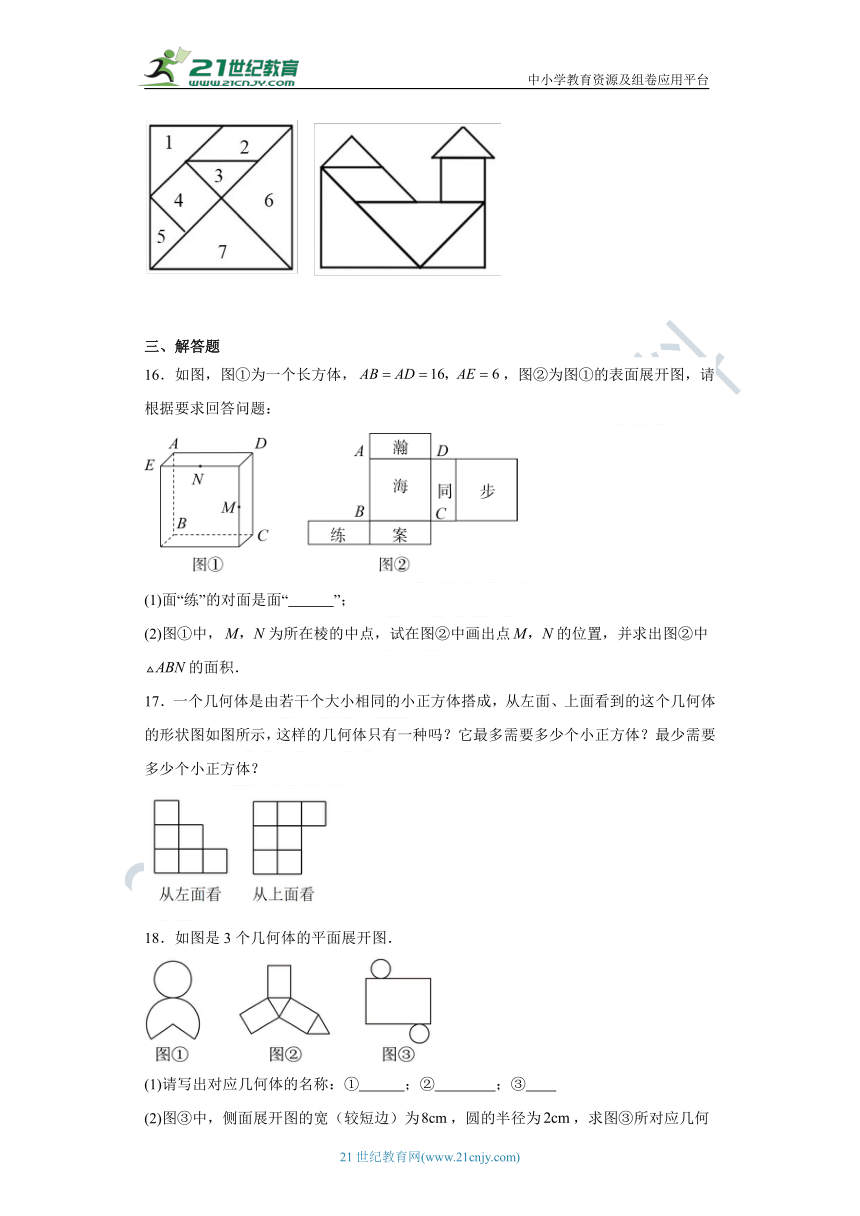
15.如图,把一副七巧板按如图进行1~7编号,1~7号分别对应着七巧板的七块,如果编号5对应的面积等于5cm2,则由这幅七巧板拼得的“房子”的面积等于 cm2.
三、解答题
16.如图,图①为一个长方体,,图②为图①的表面展开图,请根据要求回答问题:
(1)面“练”的对面是面“ ”;
(2)图①中,为所在棱的中点,试在图②中画出点的位置,并求出图②中的面积.
17.一个几何体是由若干个大小相同的小正方体搭成,从左面、上面看到的这个几何体的形状图如图所示,这样的几何体只有一种吗?它最多需要多少个小正方体?最少需要多少个小正方体?
18.如图是3个几何体的平面展开图.
(1)请写出对应几何体的名称:① ;② ;③
(2)图③中,侧面展开图的宽(较短边)为,圆的半径为,求图③所对应几何体的表面积.(结果保留)
19.如图所示,左边是小颖的圆柱形的笔筒,右边是小彬的六棱柱形的笔筒.仔细观察两个笔筒,并回答下面问题.
(1)圆柱、六棱柱各由几个面组成 它们都是平的吗
(2)圆柱的侧面与底面相交成几条线 它们是直的吗
(3)六棱柱有几个顶点 经过每个顶点有几条棱
(4)试写出圆柱与棱柱的相同点与不同点.
20.用斜二测画法画长方体直观图:
(1)补全长方体;
(2)量得的长度是 ,所表示的实际长度是 ;
(3)与棱平行的平面是 .
21.某体育中心设计一个由相同的正方形搭成的标志物(如图),每个正方体的棱长为1米,其暴露在外面的面(不包括最底层的面)用五夹板制成,然后刷漆,每张五夹板可做两个面,每平方米用漆500克.建材商店将一张五夹板按成本价提高80%后的售价标价,又以8折优惠卖出,结果每张仍获利22元(五夹板必须整张购买),所购油漆为每千克60元.
(1)制作该标志物需要多少张五夹板?
(2)购买五夹板和油漆共需多少元?
22.综合实践
【问题情景】
某综合实践小组进行废物再利用的环保小卫士行动.他们推备用废弃的宣传单制作装垃圾的无盖纸盒.
【操作探究】
(1)若准备制作一个无盖的正方体纸盒,如图1的四个图形中哪个图形经过折叠能围成无盖正方体纸盒?
.
(2)图2是小明的设计图,把它折成无盖正方体纸盒后与“保”字相对的字是 .(字在盒外)
(3)如图3,有一张边长为的正方形废弃宣传单,小华准备将其四角各剪去一个小正方形,折成无盖长方体纸盒.
①请你在如图3中画出示意图,用实线表示剪切痕迹,虚线表示折痕.
②若四角各剪去了一个边长为的小正方形,用含x的代数式表示这个纸盒的底面周长为 ;
③当四角剪去的小正方形的边长为时,请直接写出纸盒的容积.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.D
【分析】逐一判断出各选项中的几何体的名称即可得答案.
【详解】解:A是球体,不符合题意;
B是棱锥,不符合题意;
C是圆柱,不符合题意;
D是圆锥,符合题意;
故选D.
【点睛】本题考查了几何体的识别,熟练掌握常见几何体的图形特征是解题的关键.
2.C
【分析】根据图①中,共有1个小立方体,其中1个看得见,0=(1-1)3个看不见,
图②中,共有8个小立方体,其中7个看得见,1=(2-1)3个看不见,
图③中,共有27个小立方体,其中19个看得见,8=(3-1)3个看不见,…,
归纳出变化规律:
第n个图中,一切看不见的棱长为1的小立方体的个数为(n-1)3,
看见立方体的个数为n3-(n-1)3,将第11个代入即可求解.
【详解】图①中,共有1个小立方体,其中1个看得见,0=(1-1)3个看不见,
图②中,共有8个小立方体,其中7个看得见,1=(2-1)3个看不见,
图③中,共有27个小立方体,其中19个看得见,8=(3-1)3个看不见,…,
第n个图中,一切看不见的棱长为1的小立方体的个数为(n-1)3,
看见立方体的个数为n3-(n-1)3,
所以则第11个图形中,其中看得见的小立方体有113-103=331个,
故选C.
【点睛】本题主要考查图形变化规律,解决本题的关键是要通过题目条件进行归纳找出图形变化规律.
3.C
【分析】根据棱柱的定义解答即可.
【详解】解:①棱柱;②圆柱;③棱柱;④棱锥;⑤圆锥;⑥棱柱.
故选:C.
【点睛】本题主要考查的是认识立体图形,掌握棱柱的定义是解题的关键.
4.D
【分析】利用长方体的体积公式和三棱锥的体积公式即可求解.
【详解】解:长方体ABCD﹣A1B1C1D1的体积为:,
三棱锥的体积为:,
三棱锥的体积为:,
三棱锥的体积为:,
三棱锥的体积为:,
故三棱锥的体积为:,
故选D.
【点睛】本题考查了长方体和三棱锥的体积计算,将所求三棱锥的体积转化为长方体的体积与另外几个三棱锥体积的差是解题的关键.
5.C
【分析】找到从左面看的图形即可得出结果.
【详解】解:从其左面看,得到的平面图形是:
故选C.
【点睛】本题考查了从不同方向看几何体,熟练掌握从不同的方向观察几何体得到的图形形状是解题的关键.
6.D
【分析】依据长方体的展开图的特征进行判断即可.
【详解】解:A、符合长方体的展开图的特点,是长方体的展开图,故此选项符合题意;
B、符合长方体的展开图的特点,是长方体的展开图,故此选项符合题意;
C、符合长方体的展开图的特点,是长方体的展开图,故此选项符合题意;
D、不符合长方体的展开图的特点,不是长方体的展开图,故此选项不符合题意.
故选:D.
【点睛】本题考查了长方体的展开图,熟练掌握长方体的展开图的特点是解题的关键.
7.B
【分析】根据圆柱的侧面积=圆柱的底面周长×母线长(高)求解即可.
【详解】解:圆柱侧面展开图为长方形,长为圆柱的底面圆周长:,
因此,侧面积为.
故选B.
【点睛】本题考查了圆柱的侧面积,熟练掌握圆柱的侧面积公式是解题的关键.
8.C
【分析】分别将甲乙丙三位同学折成的无盖长方体的容积计算出来,即可比较大小.
【详解】甲:长方体的长为5cm,宽为3 cm,高为3 cm,容积为
乙:长方体的长为10 cm,宽为2 cm,高为2 cm,容积为
丙:长方体的长为6 cm,宽为4 cm,高为2 cm,容积为
所以,丙>甲>乙
故选C
【点睛】本题主要考查了长方体的体积,掌握长方体的体积公式是解题的关键.
9.D
【分析】根据正方体展开图的11种情况,分别进行验证,得出答案.
【详解】解:按照正方体展开图的11种情况,
分为型的6种,型的3种,型的1种,型的1种,
分别验证得,选项D能围成正方体,
故选:D.
【点睛】本题考查正方体的展开与折叠,理解和掌握正方体展开的11种结果是就问题的关键.
10.C
【分析】根据正方体的表面展开图找相对面的方法:“Z”字两端是对面,即可解答.
【详解】解:原正方体中,与“一”字所在面相对的面上的汉字是“体”,
故选:C.
【点睛】本题考查了正方体相对面上的文字,熟练掌握根据正方体的表面展开图找相对面的方法是解题的关键.
11. , ,
【分析】解答正方体表面展开图类的题目,除了提高空间想象能力外,还要掌握以下规律:
①正方体的表面展开图中,如以最长的正方形链横排为准,展开图一般是三行,个别是两行,不能是一行或四行,最长的一行(或列)在中间,可为2、3、4个正方形,超过4个或长行不在中间的不是正方体表面展开图;
②在每一行(或列)的两旁,每旁只能有1个正方形与其相连,超过1个就不是正方体表面展开图.
根据上述正方体展开图的性质即可知道3、4、5分别相对面是多少,即可解答.
【详解】正方体的表面展开图,相对的面之间一定相隔一个正方形,
∴3与6相对,4与1相对,5与2相对.
故答案为6;1;2.
【点睛】本题主要考查正方体的展开图,解题关键在于注意正方体的空间图形,从相对面入手,分析及解答问题.
12.②④
【分析】将这个展开图还原之后可以找到每个点对应的位置,这样就可以进行判断了没注意判断不要出错.
【详解】把展开图,折叠为正方体如图,依据正方体展开图的特征,②④是正确的,
故答案为②④.
【点睛】本题主要考查了空间几何体的展开图,我们将这个展开图还原之后可以找到每个点对应的位置,这样就可以进行判断了没注意判断不要出错.
13.4
【分析】根据正方体展开图的特点涂色即可.
【详解】如图,由四种不同的涂法.
故答案为4.
【点睛】本题考查了正方体的展开图及学生的空间想象能力,正方体展开图规律:十一种类看仔细,中间四个成一行,两边各一无规矩;二三紧连错一个,三一相连一随意;两两相连各错一,三个两排一对齐;一条线上不过四,田七和凹要放弃.
14.9
【分析】把可以分得的边长为整数的长方形(或正方形)按照面积从小到大排列有:,,,, ,,,,,,,,,,若能分成5张满足条件的纸片,因为其面积之和正好为20,依此找到满足条件的情况数即可求解.
【详解】解:把可以分得的边长为整数的长方形(或正方形)按照面积从小到大排列有: ,,,, ,,,,,,,,,,若能分成5张满足条件的纸片,因为其面积之和正好为20,
那么满足条件的有:,,,,;
,,,,;
,,,,;
,,,,;
,,,,;
,,,,;
,,,,;
,,,,;
,,,,;
故这样的5张长方形纸片共有9种.
故答案为:9.
【点睛】本题考查了认识平面图形,解题的关键是找到5张满足条件的纸片,其面积之和正好为20.
15.80
【分析】将七巧板进行分割,分成16个面积相等的三角形,从而计算即可.
【详解】解:如图,将七巧板进行如下分割,可将七巧板分成16个面积相等的三角形,
其中编号5对应的面积为5cm2,
∴由这个七巧板拼成的正方形的面积为:
16×5=80cm2,
则拼成的“房子”的面积为80cm2,
故答案为:80.
【点睛】本题考查了图形的剪拼,七巧板的性质,解题的关键是明确七巧板的构成,以及每块的面积与整个七巧板的关系.
16.(1)同
(2)位置见详解,或者
【分析】(1)正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答;
(2)根据点M、N在与正方形相邻的两个面的边上确定出点M、N的位置即可;求出点N到的距离,再利用三角形的面积公式列式计算即可得解.
【详解】(1)正方体的表面展开图,相对的面之间一定相隔一个正方形,
“练”与“同”是相对面,
“海”与“步”是相对面,
“瀚”与“案”是相对面,
答:面“练”的对面是面“同”.
(2)点M、N如图所示,
N点有、两个点,M点只有一个点,
当N点在时,
∵N是所在棱的中点,,
∴点到AB的距离为,
∴的面积;
当N点在时,
∵N是所在棱的中点,,
∴点到AB的距离为,
∴的面积,
故的面积为或者.
【点睛】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.解答时,注意N点有、两个点,需要分类讨论.
17.不止一种,最多需要15个小正方体,最少需要10个小正方体
【分析】利用从上看的图形,在从上面看到的图上写出最多以及最少时小正方体的个数,可得结论.
【详解】结合左面看到的几何体,在从上面看到的图上写出最多以及最少时小正方体的个数,如图:
最多有:(个),
最少有:(个),
即可知:这样的几何体不止一种,最多需要15个小正方体,最少需要10个小正方体.
【点睛】本题考查从不同角度观看几何体的知识,解题的关键是具有一定的空间想象力,属于中考常考题型.
18.(1)圆锥;三棱柱;圆柱
(2)
【分析】(1)根据几何体的展开图,可得答案;
(2)根据圆柱的表面积公式,可得答案.
【详解】(1)解:对应几何体的名称:①圆锥;②三棱柱;③圆柱.
故答案为:圆锥;三棱柱;圆柱.
(2)∵侧面展开图的宽(较短边)为,圆的半径为,
∴圆柱的表面积为:
.
∴图③所对应几何体的表面积.
【点睛】本题考查几何体的展开图和圆柱的表面积.熟练掌握几何体的展开图及圆柱表面积的计算公式是解题的关键.
19.(1)见解析
(2)见解析
(3)见解析
(4)见解析
【分析】(1)根据圆柱由两个底面和一个侧面组成,六棱柱由两个底面和六个侧面组成回答即可;
(2)根据圆柱的侧面与底面相交成一条曲线回答即可;
(3)根据六棱柱两个底面是六边形可确定顶点的个数,观察图形可知经过每个顶点有三条棱;
(4)根据两个立体图形的底面和侧面的联系与区别回答即可;
【详解】(1)解:圆柱由两个底面和一个侧面组成,底面是平面,侧面是曲面;六棱柱由两个底面和六个侧面组成,都是平面.
(2)解:圆柱的侧面与上下两个底面相交各成一条线,是个圆,它是曲线.
(3)解:六棱柱两个底面是六边形,故共有12个顶点;
经过每个顶点有三条棱.
(4)解:棱柱与圆柱的相同点是:都是柱体,都有两个底面;
不同点是:棱柱与圆柱的底面形状不同,棱柱的底面是多边形,圆柱的底面是圆形,圆柱的侧面是曲面,而棱柱的侧面是长方形.
【点睛】本题主要考查的是认识立体图形,认真观察图形是解题的关键.
20.(1)作图见解析
(2);
(3)平面、平面
【分析】(1)利用斜二测画法首先建立坐标系,再利用图像各边与坐标轴位置关系画出图像即可;
(2)利用刻度尺量出的长度为,再利用斜二测法所化图形的性质得出实际长度;
(3)利用图像得出与棱平行的平面即可.
【详解】(1)解:如图所示.
(2)∵用刻度尺量出的长度为,
∴表示的实际长度是,
故答案为:;.
(3)与棱平行的平面是:平面、平面.
故答案为:平面、平面.
【点睛】本题考查斜二测法画立体图形以及直线与面平行的性质,根据已知图像建立坐标,再画出图形是解题关键.
21.(1)制作该标志物需要25张五夹板.
(2)购买五夹板和油漆共需3300元钱.
【分析】(1)依次数出前面,后面,左面,右面,上面的个数,相加后除以2,即可求出需要五夹板的张数;
(2)先分别求出油漆应付款和五夹板需付费,再相加即可.
【详解】(1)解:暴露在外面的面共有:(面),
需购五夹板数:(张);
答:制作该标志物需要25张五夹板.
(2)解:500克即千克,
需购油漆数:(千克),
购油漆应付款:(元),
设五夹板的成本价为x元/张,根据题意得:
,
解得:,
则每张五夹板售价为:(元),
购五夹板需付费:(元),
因此购五夹板和油漆共需费用:(元).
答:购买五夹板和油漆共需3300元钱.
【点睛】本题考查了应用一元一次方程的解决实际问题的能力,要细心的理解题意才行.第(2)题要理解成本价、标价、售价之间的关系及打折的含义.
22.(1)C
(2)卫
(3)①图形见解析;②;③纸盒的容积为
【分析】(1)根据正方体的折叠可知有5个面,再依据正方体的展开图即可可得答案;
(2)根据正方体的表面展开图的特征,即可得到答案;
(3)①根据题意画出相应的图形即可得到答案;②根据题意可知,底面是边长为的正方形,利用周长公式计算即可得到答案;③先表示出折叠后的长方体的体积,再把代入求值即可得到答案.
【详解】(1)解:折叠成一个无盖的正方体纸盒,
展开图有5个面,B、D选项中的图形不符合题意,
再根据正方体的展开图的特征,A选项中的图形不符合题意,
选项C中的图形能够折叠成一个无盖的正方体纸盒,
故答案为:C;
(2)解:正方体的平面展开图中,相对面的特点是中间必须间隔一个正方形,
与“保”字相对的字是“卫”,
故答案为:卫;
(3)解:①图形如图所示:
②边长为的正方形,四角各剪去了一个边长为的小正方形,
底面是边长为的正方形,
周长为,
故答案为:;
③由图形可知,折叠后的长方体的底面是边长为的正方形,高为,
体积为,
当时,
(20﹣2x)2x
=(20﹣2×4)2×4
=576(cm3),
答:当小正方形边长为时,纸盒的容积为.
【点睛】本题考查正方体的表面展开图,列代数式并求值,掌握正方体的表面展开图的特征是解决问题的关键.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
七年级数学上册 第四章
4.1.1 立体图形与平面图形 同步练习题
一、单选题
1.下列立体图形中,是圆锥的是( )
A. B. C. D.
2.如图所示,每个小立方体的棱长为1,按如图所示的视线方向看,图1中共有1个1立方体,其中1个看得见,0个看不见;图2中共有8个立方体,其中7个看得见,1个看不见;图3中共有27个小立方体,其中19个看得见,8个看不见;…,则第11个图形中,其中看得见的小立方体个数是( )
A.271 B.272 C.331 D.332
3.下列几何中,属于棱柱的是( )
① ② ③ ④ ⑤ ⑥
A.①③ B.① C.①③⑥ D.①⑥
4.如图,在长方体ABCD﹣A1B1C1D1中,已知AB=4,AD=3,AA1=2.则三棱锥C1﹣A1DB的体积为( )
A.24 B.16 C.12 D.8
5.如图是一个由5个相同的正方体组成的立体图形,从其左面看,得到的平面图形是( )
A. B.
C. D.
6.将如图所示的长方体包装盒沿某些棱剪开,且使六个面连在一起,然后铺平,则得到的图形不可能是( )
A. B.
C. D.
7.已知圆柱的底面半径为3cm,母线长为5cm,则圆柱的侧面积是
A. B. C. D.
8.在课题学习中,老师要求用长为12厘米,宽为8厘米的长方形纸片制作一个无盖的长方体纸盒.三位同学分别以下列方式在长方形纸片上截去两角(图中阴影部分),然后沿虚线折成一个无盖的长方体纸盒.
甲:如图1,盒子底面的四边形ABCD是正方形;
乙:如图2,盒子底面的四边形ABCD是正方形;
丙:如图3,盒子底面的四边形ABCD是长方形,AB=2AD.
将这三位同学所折成的无盖长方体的容积按从大到小的顺序排列,正确的是
A.甲>乙>丙 B.甲>丙>乙 C.丙>甲>乙 D.丙>乙>甲
9.下列图形经过折叠,能够围成正方体的是( )
A. B.
C. D.
10.第19届亚运会将于2023年9月23日至2023年10月8日在杭州举行,中国代表队自1982年新德里亚运会以来,连续蝉联金牌榜第一,中国已经成为亚洲体育第一强国.小明将“亚、洲、体、育、第、一”这六个汉字分别写在某正方体的表面上,如图是它的一种展开图,现在原正方体中,与“一”字所在面相对的面上的汉字是( )
A.亚 B.洲 C.体 D.育
二、填空题
11.如图在正方体的展开图上编号,请你写出相对面的号码: 的相对面是 , 的相对面是 , 的相对面是 .
12.如图,这是一个正方体的表面展开图,若把它再折回成正方体后,有下列命题:
①点H与点C重合;②点D与点M与点R重合;③点B与点Q重合;④点A与点S重合.
其中正确命题的序号是 .(注:把你认为正确的命题的序号都填上)
13.在下图的网格中选择一个涂上阴影,使全部阴影图形经折叠后能够形成一个正方体,一共有 种不同的涂法.
14.有一张长和宽分别是5和4的长方形纸片,现在把它正好分成5张形状各不相同的长方形(包括正方形)纸片,且每张纸片的边长都为整数.这样的5张长方形纸片共有 种.
15.如图,把一副七巧板按如图进行1~7编号,1~7号分别对应着七巧板的七块,如果编号5对应的面积等于5cm2,则由这幅七巧板拼得的“房子”的面积等于 cm2.
三、解答题
16.如图,图①为一个长方体,,图②为图①的表面展开图,请根据要求回答问题:
(1)面“练”的对面是面“ ”;
(2)图①中,为所在棱的中点,试在图②中画出点的位置,并求出图②中的面积.
17.一个几何体是由若干个大小相同的小正方体搭成,从左面、上面看到的这个几何体的形状图如图所示,这样的几何体只有一种吗?它最多需要多少个小正方体?最少需要多少个小正方体?
18.如图是3个几何体的平面展开图.
(1)请写出对应几何体的名称:① ;② ;③
(2)图③中,侧面展开图的宽(较短边)为,圆的半径为,求图③所对应几何体的表面积.(结果保留)
19.如图所示,左边是小颖的圆柱形的笔筒,右边是小彬的六棱柱形的笔筒.仔细观察两个笔筒,并回答下面问题.
(1)圆柱、六棱柱各由几个面组成 它们都是平的吗
(2)圆柱的侧面与底面相交成几条线 它们是直的吗
(3)六棱柱有几个顶点 经过每个顶点有几条棱
(4)试写出圆柱与棱柱的相同点与不同点.
20.用斜二测画法画长方体直观图:
(1)补全长方体;
(2)量得的长度是 ,所表示的实际长度是 ;
(3)与棱平行的平面是 .
21.某体育中心设计一个由相同的正方形搭成的标志物(如图),每个正方体的棱长为1米,其暴露在外面的面(不包括最底层的面)用五夹板制成,然后刷漆,每张五夹板可做两个面,每平方米用漆500克.建材商店将一张五夹板按成本价提高80%后的售价标价,又以8折优惠卖出,结果每张仍获利22元(五夹板必须整张购买),所购油漆为每千克60元.
(1)制作该标志物需要多少张五夹板?
(2)购买五夹板和油漆共需多少元?
22.综合实践
【问题情景】
某综合实践小组进行废物再利用的环保小卫士行动.他们推备用废弃的宣传单制作装垃圾的无盖纸盒.
【操作探究】
(1)若准备制作一个无盖的正方体纸盒,如图1的四个图形中哪个图形经过折叠能围成无盖正方体纸盒?
.
(2)图2是小明的设计图,把它折成无盖正方体纸盒后与“保”字相对的字是 .(字在盒外)
(3)如图3,有一张边长为的正方形废弃宣传单,小华准备将其四角各剪去一个小正方形,折成无盖长方体纸盒.
①请你在如图3中画出示意图,用实线表示剪切痕迹,虚线表示折痕.
②若四角各剪去了一个边长为的小正方形,用含x的代数式表示这个纸盒的底面周长为 ;
③当四角剪去的小正方形的边长为时,请直接写出纸盒的容积.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.D
【分析】逐一判断出各选项中的几何体的名称即可得答案.
【详解】解:A是球体,不符合题意;
B是棱锥,不符合题意;
C是圆柱,不符合题意;
D是圆锥,符合题意;
故选D.
【点睛】本题考查了几何体的识别,熟练掌握常见几何体的图形特征是解题的关键.
2.C
【分析】根据图①中,共有1个小立方体,其中1个看得见,0=(1-1)3个看不见,
图②中,共有8个小立方体,其中7个看得见,1=(2-1)3个看不见,
图③中,共有27个小立方体,其中19个看得见,8=(3-1)3个看不见,…,
归纳出变化规律:
第n个图中,一切看不见的棱长为1的小立方体的个数为(n-1)3,
看见立方体的个数为n3-(n-1)3,将第11个代入即可求解.
【详解】图①中,共有1个小立方体,其中1个看得见,0=(1-1)3个看不见,
图②中,共有8个小立方体,其中7个看得见,1=(2-1)3个看不见,
图③中,共有27个小立方体,其中19个看得见,8=(3-1)3个看不见,…,
第n个图中,一切看不见的棱长为1的小立方体的个数为(n-1)3,
看见立方体的个数为n3-(n-1)3,
所以则第11个图形中,其中看得见的小立方体有113-103=331个,
故选C.
【点睛】本题主要考查图形变化规律,解决本题的关键是要通过题目条件进行归纳找出图形变化规律.
3.C
【分析】根据棱柱的定义解答即可.
【详解】解:①棱柱;②圆柱;③棱柱;④棱锥;⑤圆锥;⑥棱柱.
故选:C.
【点睛】本题主要考查的是认识立体图形,掌握棱柱的定义是解题的关键.
4.D
【分析】利用长方体的体积公式和三棱锥的体积公式即可求解.
【详解】解:长方体ABCD﹣A1B1C1D1的体积为:,
三棱锥的体积为:,
三棱锥的体积为:,
三棱锥的体积为:,
三棱锥的体积为:,
故三棱锥的体积为:,
故选D.
【点睛】本题考查了长方体和三棱锥的体积计算,将所求三棱锥的体积转化为长方体的体积与另外几个三棱锥体积的差是解题的关键.
5.C
【分析】找到从左面看的图形即可得出结果.
【详解】解:从其左面看,得到的平面图形是:
故选C.
【点睛】本题考查了从不同方向看几何体,熟练掌握从不同的方向观察几何体得到的图形形状是解题的关键.
6.D
【分析】依据长方体的展开图的特征进行判断即可.
【详解】解:A、符合长方体的展开图的特点,是长方体的展开图,故此选项符合题意;
B、符合长方体的展开图的特点,是长方体的展开图,故此选项符合题意;
C、符合长方体的展开图的特点,是长方体的展开图,故此选项符合题意;
D、不符合长方体的展开图的特点,不是长方体的展开图,故此选项不符合题意.
故选:D.
【点睛】本题考查了长方体的展开图,熟练掌握长方体的展开图的特点是解题的关键.
7.B
【分析】根据圆柱的侧面积=圆柱的底面周长×母线长(高)求解即可.
【详解】解:圆柱侧面展开图为长方形,长为圆柱的底面圆周长:,
因此,侧面积为.
故选B.
【点睛】本题考查了圆柱的侧面积,熟练掌握圆柱的侧面积公式是解题的关键.
8.C
【分析】分别将甲乙丙三位同学折成的无盖长方体的容积计算出来,即可比较大小.
【详解】甲:长方体的长为5cm,宽为3 cm,高为3 cm,容积为
乙:长方体的长为10 cm,宽为2 cm,高为2 cm,容积为
丙:长方体的长为6 cm,宽为4 cm,高为2 cm,容积为
所以,丙>甲>乙
故选C
【点睛】本题主要考查了长方体的体积,掌握长方体的体积公式是解题的关键.
9.D
【分析】根据正方体展开图的11种情况,分别进行验证,得出答案.
【详解】解:按照正方体展开图的11种情况,
分为型的6种,型的3种,型的1种,型的1种,
分别验证得,选项D能围成正方体,
故选:D.
【点睛】本题考查正方体的展开与折叠,理解和掌握正方体展开的11种结果是就问题的关键.
10.C
【分析】根据正方体的表面展开图找相对面的方法:“Z”字两端是对面,即可解答.
【详解】解:原正方体中,与“一”字所在面相对的面上的汉字是“体”,
故选:C.
【点睛】本题考查了正方体相对面上的文字,熟练掌握根据正方体的表面展开图找相对面的方法是解题的关键.
11. , ,
【分析】解答正方体表面展开图类的题目,除了提高空间想象能力外,还要掌握以下规律:
①正方体的表面展开图中,如以最长的正方形链横排为准,展开图一般是三行,个别是两行,不能是一行或四行,最长的一行(或列)在中间,可为2、3、4个正方形,超过4个或长行不在中间的不是正方体表面展开图;
②在每一行(或列)的两旁,每旁只能有1个正方形与其相连,超过1个就不是正方体表面展开图.
根据上述正方体展开图的性质即可知道3、4、5分别相对面是多少,即可解答.
【详解】正方体的表面展开图,相对的面之间一定相隔一个正方形,
∴3与6相对,4与1相对,5与2相对.
故答案为6;1;2.
【点睛】本题主要考查正方体的展开图,解题关键在于注意正方体的空间图形,从相对面入手,分析及解答问题.
12.②④
【分析】将这个展开图还原之后可以找到每个点对应的位置,这样就可以进行判断了没注意判断不要出错.
【详解】把展开图,折叠为正方体如图,依据正方体展开图的特征,②④是正确的,
故答案为②④.
【点睛】本题主要考查了空间几何体的展开图,我们将这个展开图还原之后可以找到每个点对应的位置,这样就可以进行判断了没注意判断不要出错.
13.4
【分析】根据正方体展开图的特点涂色即可.
【详解】如图,由四种不同的涂法.
故答案为4.
【点睛】本题考查了正方体的展开图及学生的空间想象能力,正方体展开图规律:十一种类看仔细,中间四个成一行,两边各一无规矩;二三紧连错一个,三一相连一随意;两两相连各错一,三个两排一对齐;一条线上不过四,田七和凹要放弃.
14.9
【分析】把可以分得的边长为整数的长方形(或正方形)按照面积从小到大排列有:,,,, ,,,,,,,,,,若能分成5张满足条件的纸片,因为其面积之和正好为20,依此找到满足条件的情况数即可求解.
【详解】解:把可以分得的边长为整数的长方形(或正方形)按照面积从小到大排列有: ,,,, ,,,,,,,,,,若能分成5张满足条件的纸片,因为其面积之和正好为20,
那么满足条件的有:,,,,;
,,,,;
,,,,;
,,,,;
,,,,;
,,,,;
,,,,;
,,,,;
,,,,;
故这样的5张长方形纸片共有9种.
故答案为:9.
【点睛】本题考查了认识平面图形,解题的关键是找到5张满足条件的纸片,其面积之和正好为20.
15.80
【分析】将七巧板进行分割,分成16个面积相等的三角形,从而计算即可.
【详解】解:如图,将七巧板进行如下分割,可将七巧板分成16个面积相等的三角形,
其中编号5对应的面积为5cm2,
∴由这个七巧板拼成的正方形的面积为:
16×5=80cm2,
则拼成的“房子”的面积为80cm2,
故答案为:80.
【点睛】本题考查了图形的剪拼,七巧板的性质,解题的关键是明确七巧板的构成,以及每块的面积与整个七巧板的关系.
16.(1)同
(2)位置见详解,或者
【分析】(1)正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答;
(2)根据点M、N在与正方形相邻的两个面的边上确定出点M、N的位置即可;求出点N到的距离,再利用三角形的面积公式列式计算即可得解.
【详解】(1)正方体的表面展开图,相对的面之间一定相隔一个正方形,
“练”与“同”是相对面,
“海”与“步”是相对面,
“瀚”与“案”是相对面,
答:面“练”的对面是面“同”.
(2)点M、N如图所示,
N点有、两个点,M点只有一个点,
当N点在时,
∵N是所在棱的中点,,
∴点到AB的距离为,
∴的面积;
当N点在时,
∵N是所在棱的中点,,
∴点到AB的距离为,
∴的面积,
故的面积为或者.
【点睛】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.解答时,注意N点有、两个点,需要分类讨论.
17.不止一种,最多需要15个小正方体,最少需要10个小正方体
【分析】利用从上看的图形,在从上面看到的图上写出最多以及最少时小正方体的个数,可得结论.
【详解】结合左面看到的几何体,在从上面看到的图上写出最多以及最少时小正方体的个数,如图:
最多有:(个),
最少有:(个),
即可知:这样的几何体不止一种,最多需要15个小正方体,最少需要10个小正方体.
【点睛】本题考查从不同角度观看几何体的知识,解题的关键是具有一定的空间想象力,属于中考常考题型.
18.(1)圆锥;三棱柱;圆柱
(2)
【分析】(1)根据几何体的展开图,可得答案;
(2)根据圆柱的表面积公式,可得答案.
【详解】(1)解:对应几何体的名称:①圆锥;②三棱柱;③圆柱.
故答案为:圆锥;三棱柱;圆柱.
(2)∵侧面展开图的宽(较短边)为,圆的半径为,
∴圆柱的表面积为:
.
∴图③所对应几何体的表面积.
【点睛】本题考查几何体的展开图和圆柱的表面积.熟练掌握几何体的展开图及圆柱表面积的计算公式是解题的关键.
19.(1)见解析
(2)见解析
(3)见解析
(4)见解析
【分析】(1)根据圆柱由两个底面和一个侧面组成,六棱柱由两个底面和六个侧面组成回答即可;
(2)根据圆柱的侧面与底面相交成一条曲线回答即可;
(3)根据六棱柱两个底面是六边形可确定顶点的个数,观察图形可知经过每个顶点有三条棱;
(4)根据两个立体图形的底面和侧面的联系与区别回答即可;
【详解】(1)解:圆柱由两个底面和一个侧面组成,底面是平面,侧面是曲面;六棱柱由两个底面和六个侧面组成,都是平面.
(2)解:圆柱的侧面与上下两个底面相交各成一条线,是个圆,它是曲线.
(3)解:六棱柱两个底面是六边形,故共有12个顶点;
经过每个顶点有三条棱.
(4)解:棱柱与圆柱的相同点是:都是柱体,都有两个底面;
不同点是:棱柱与圆柱的底面形状不同,棱柱的底面是多边形,圆柱的底面是圆形,圆柱的侧面是曲面,而棱柱的侧面是长方形.
【点睛】本题主要考查的是认识立体图形,认真观察图形是解题的关键.
20.(1)作图见解析
(2);
(3)平面、平面
【分析】(1)利用斜二测画法首先建立坐标系,再利用图像各边与坐标轴位置关系画出图像即可;
(2)利用刻度尺量出的长度为,再利用斜二测法所化图形的性质得出实际长度;
(3)利用图像得出与棱平行的平面即可.
【详解】(1)解:如图所示.
(2)∵用刻度尺量出的长度为,
∴表示的实际长度是,
故答案为:;.
(3)与棱平行的平面是:平面、平面.
故答案为:平面、平面.
【点睛】本题考查斜二测法画立体图形以及直线与面平行的性质,根据已知图像建立坐标,再画出图形是解题关键.
21.(1)制作该标志物需要25张五夹板.
(2)购买五夹板和油漆共需3300元钱.
【分析】(1)依次数出前面,后面,左面,右面,上面的个数,相加后除以2,即可求出需要五夹板的张数;
(2)先分别求出油漆应付款和五夹板需付费,再相加即可.
【详解】(1)解:暴露在外面的面共有:(面),
需购五夹板数:(张);
答:制作该标志物需要25张五夹板.
(2)解:500克即千克,
需购油漆数:(千克),
购油漆应付款:(元),
设五夹板的成本价为x元/张,根据题意得:
,
解得:,
则每张五夹板售价为:(元),
购五夹板需付费:(元),
因此购五夹板和油漆共需费用:(元).
答:购买五夹板和油漆共需3300元钱.
【点睛】本题考查了应用一元一次方程的解决实际问题的能力,要细心的理解题意才行.第(2)题要理解成本价、标价、售价之间的关系及打折的含义.
22.(1)C
(2)卫
(3)①图形见解析;②;③纸盒的容积为
【分析】(1)根据正方体的折叠可知有5个面,再依据正方体的展开图即可可得答案;
(2)根据正方体的表面展开图的特征,即可得到答案;
(3)①根据题意画出相应的图形即可得到答案;②根据题意可知,底面是边长为的正方形,利用周长公式计算即可得到答案;③先表示出折叠后的长方体的体积,再把代入求值即可得到答案.
【详解】(1)解:折叠成一个无盖的正方体纸盒,
展开图有5个面,B、D选项中的图形不符合题意,
再根据正方体的展开图的特征,A选项中的图形不符合题意,
选项C中的图形能够折叠成一个无盖的正方体纸盒,
故答案为:C;
(2)解:正方体的平面展开图中,相对面的特点是中间必须间隔一个正方形,
与“保”字相对的字是“卫”,
故答案为:卫;
(3)解:①图形如图所示:
②边长为的正方形,四角各剪去了一个边长为的小正方形,
底面是边长为的正方形,
周长为,
故答案为:;
③由图形可知,折叠后的长方体的底面是边长为的正方形,高为,
体积为,
当时,
(20﹣2x)2x
=(20﹣2×4)2×4
=576(cm3),
答:当小正方形边长为时,纸盒的容积为.
【点睛】本题考查正方体的表面展开图,列代数式并求值,掌握正方体的表面展开图的特征是解决问题的关键.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
