4.3.3 余角和补角同步练习题(含解析)
文档属性
| 名称 | 4.3.3 余角和补角同步练习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 915.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-05 09:47:43 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
七年级数学上册 第四章 4.3.3 余角和补角 同步练习题
一、单选题
1.已知与互余,若,则( )
A. B. C. D.
2.若,则的余角是( )
A. B. C. D.
3.若,则∠A的补角为( )
A.40° B.50° C.120° D.130°
4.如果一个角的补角是,则这个角为( )
A. B. C. D.
5.一个角补角是它的余角的4倍,这个角的度数是( )
A.135° B.45° C.60° D.30°
6.下列说法中正确的个数是( )
①锐角的补角一定是钝角;②一个角的补角一定大于这个角;③已知线段,,则点P在直线外;④若,则点B为线段的中点.
A.1 B.2 C.3 D.4
7.一个角的补角比这个角的余角 倍还多,则这个角的度数为( )
A. B. C. D.
8.如图,射线表示北偏东方向,射线表示南偏西方向,则的度数是( )
A. B. C. D.
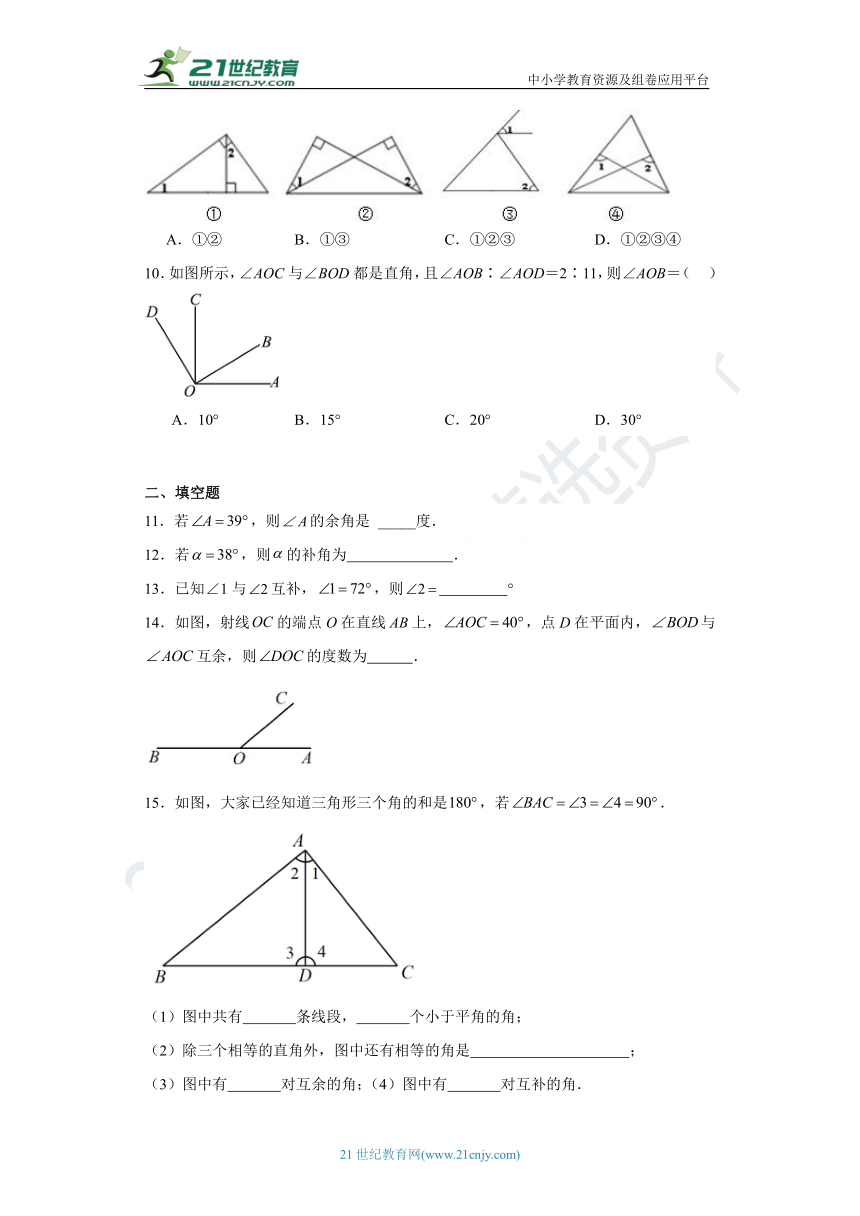
9.根据图中给定的条件,下列各图中可以判断∠1与∠2一定相等的是( )
A.①② B.①③ C.①②③ D.①②③④
10.如图所示,∠AOC与∠BOD都是直角,且∠AOB∶∠AOD=2∶11,则∠AOB=( )
A.10° B.15° C.20° D.30°
二、填空题
11.若,则的余角是 _____度.
12.若,则的补角为 .
13.已知∠1与互补,,则 °
14.如图,射线的端点O在直线上,,点D在平面内,与互余,则的度数为 .
15.如图,大家已经知道三角形三个角的和是,若.
(1)图中共有 条线段, 个小于平角的角;
(2)除三个相等的直角外,图中还有相等的角是 ;
(3)图中有 对互余的角;(4)图中有 对互补的角.
三、解答题
16.点O是直线上的点,,射线是的平分线.
(1)位置如图1时,用等式与的数量关系,并说明理由;
(2)位置如图2时,(1)中与的数量关系是否仍然成立?若成立,请说明理由;若不成立,请写出你得到的结论,并说明理由.
17.如图,已知锐角,把一个三角尺的直角顶点与点重合,一条直角边和重合,沿另一条直角边在射线的同侧画射线,再用量角器画出的平分线,此时,与互余.
(1)请你画出图形,用所学知识说明与互余;
(2)请你仿照上面互为余角的画法,在图2中画出一个,使与互补,并简要说明画图方法;若,求的度数.
18.如图,直线、相交于点O,平分,于点O,,求的度数.
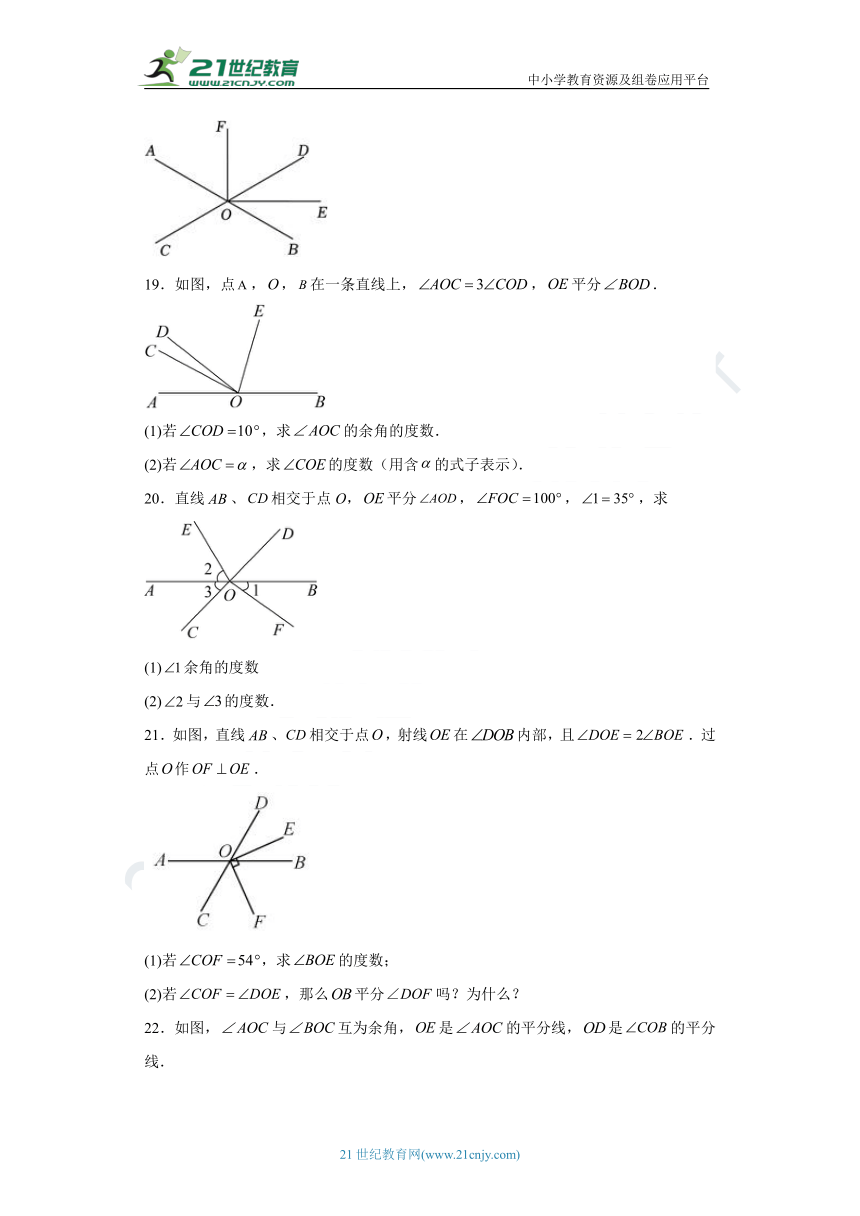
19.如图,点,,在一条直线上,,平分.
(1)若,求的余角的度数.
(2)若,求的度数(用含的式子表示).
20.直线、相交于点O,平分,,,求
(1)余角的度数
(2)与的度数.
21.如图,直线、相交于点,射线在内部,且.过点作.
(1)若,求的度数;
(2)若,那么平分吗?为什么?
22.如图,与互为余角,是的平分线,是的平分线.
(1)若,求的度数;
(2)若,求的度数.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.D
【分析】根据互余的定义,即可进行解答.如果两个角相加等于,那么这两个角互余.
【详解】解:∵与互余,若,
∴,
故选:D.
【点睛】本题主要考查了互余的定义,解题的关键是掌握如果两个角相加等于,那么这两个角互余.
2.C
【分析】用即可求解.
【详解】解:,则的余角是,
故选:C.
【点睛】本题考查的是余角的定义,即如果两个角的和等于(直角),就说这两个角互为余角.即其中一个角是另一个角的余角,解题关键是掌握余角的定义.
3.D
【分析】根据互为补角的两个角的和等于列式计算即可得解.
【详解】解:的补角.
故选:D.
【点睛】本题考查了补角,熟记补角的概念是解题的关键.
4.D
【分析】根据补角的定义即可进行解答.
【详解】解:,
故选:D.
【点睛】本题主要考查了补角的定义,解题的关键是掌握“如果两个角相加等于,则这两个角互为补角”.
5.C
【分析】设这个角的度数为,则它的余角为,它的补角为,再根据一个角补角是它的余角的4倍,列出方程求解即可.
【详解】解:设这个角的度数为,则它的余角为,它的补角为,
由题意得,,
解得,
∴这个角的度数为60°,
故选C.
【点睛】本题主要考查了与余角和补角有关的计算,解题的关键在于熟知:如果两个角的度数之和为90度,那么这两个角互余;如果两个角的度数之和为180度,那么这两个角互补.
6.A
【分析】根据补角的定义,线段中点的性质,点与直线的位置关系,逐项分析判断即可求解.
【详解】解:①锐角的补角一定是钝角,故①正确;
②一个角的补角不一定大于这个角,例如角的补角等于,故②不正确;
③已知线段,,则点P在直线外或在直线上,故③不正确;
④若,且点在线段上,则点B为线段的中点,故④不正确,
故选:A.
【点睛】本题考查了补角的定义,线段中点的性质,点与直线的位置关系,掌握以上知识是解题的关键.
7.B
【分析】设这个角的度数为,根据题意列出方程,解方程即可求解.
【详解】解:设这个角的度数为,则这个角的补角为,这个角的余角为,根据题意得,
解得:,
故选:B.
【点睛】本题考查了与补角、余角相关的计算,一元一次方程的应用,根据题意列出方程是解题的关键.
8.C
【分析】先求出的余角,然后再加上与的和进行计算即可解答.
【详解】解:由题意得:
∵,
∴,
∴的度数是.
故选:C.
【点睛】本题考查方向角,余角,角的和差计算.根据题目的已知条件并结合图形分析是解题的关键.
9.A
【分析】根据同角或等角的余角相等,即可判断①和②,无法判断③和④.
【详解】解:如图①,
∵∠1+∠3=90°,∠2+∠3=90°,
∴∠1=∠2;
如图②,
∵∠1+∠3=90°,∠2+∠4=90°,∠3=∠4,
∴∠1=∠2;
如图③,无法证明∠1=∠2,
如图④,无法证明∠1=∠2,
故选:A
【点睛】此题考查了同角或等角的余角相等,熟练掌握余角的性质是解题的关键.
10.C
【分析】由∠AOB+∠BOC=∠BOC+∠COD知∠AOB=∠COD,设∠AOB=2α,则∠AOD=11α,故∠AOB+∠BOC=9α=90°,解得α,从而可求解.
【详解】解:∵∠AOC与∠BOD都是直角,
∴∠AOB+∠BOC=∠BOC+∠COD=90°,
∴∠AOB=∠COD, 设∠AOB=2α,
∵∠AOB:∠AOD=2:11,
∴
∴∠AOB+∠BOC=9α=90°,
解得α=10°,
∴∠AOB=20°.
故选:C.
【点睛】本题主要考查了几何图形中角的计算以及余角和补角,正确表示出各角度数是解题关键.
11.
【分析】利用余角的定义进行求解即可.
【详解】解:,
的余角为:.
故答案为:.
【点睛】本题主要考查余角,解答的关键是明确互为余角的两角之和为.
12./度
【分析】根据和为的两个角互为补角进行求解即可.
【详解】解:∵,
∴的补角为,
故答案为:.
【点睛】本题考查了补角的定义,熟知和为的两个角互为补角是解本题的关键.
13.108
【分析】根据和为的两个角互为补角,根据定义解答.
【详解】解:∵∠1与互补,
∴,
∵,
∴,
故答案为:.
【点睛】此题考查了补角的定义,熟记定义是解题的关键.
14.或
【分析】分两种情况讨论:①在直线上方;②在直线下方,再利用角之间的关系可以求解.
【详解】解:①当在直线上方时,如图,
∵与互余,
∴,
∴;
②当在直线的下方时,如图,
∵与互余,
∴,
∴,
∵,
∴
故答案为:或.
【点睛】本题主要考查余角与补角,解答的关键是结合图形分析清楚角与角之间的关系.
15. 6 7 , 4 3
【分析】(1)根据线段定义:直线上两个点和它们之间的部分叫做线段,写出图中线段,再写出图中小于的角即可;
(2)根据互为余角得出图中相等的角即可;
(3)根据两角相加等于的两个角互为余角,判断即可;
(4)两脚相加等于的两个角互为补角,判断即可.
【详解】解:(1)图中的线段有:,共条线段,
小于平角的角有:,共个;
(2)∵,
∴,
∵,
∴,
∴图中相等的角还有: ,;
(3)图中互余的角有:和,和,和,和,
共对;
(4)图中互补的角为:和,和,和,共对;
故答案为:6;7;,;4;3.
【点睛】本题考查了线段的定义,平角的概念,余角的概念,补角的概念等知识点,熟知定义是解决本题的关键.
16.(1);理由见解析
(2)不成立,,理由见解析
【分析】(1)由题意知,,设,则,,可得,,进而可得与的关系;
(2)同(1)分别用含的代数式表示出,,然后通过加法运算求二者的关系即可;
【详解】(1)解:,理由如下:
∵射线是的平分线,
∴,
设,则,,
∴,,
∴;
(2)解:不成立,,理由如下:
∵射线是的平分线,
∴,
设,则,,
∴,,
∵,
∴.
【点睛】本题考查了角平分线,与余角、补角有关的计算等知识.解题的关键在于明确角度之间的数量关系.
17.(1)图见解析,证明见解析
(2)图见解析,
【分析】(1)根据角平分线的定义和余角的性质即可得答案;
(2)作的延长线,作的角平分线,利用角平分线的定义和补角的性质即可得答案.
【详解】(1)解:如下图,
因为平分,
所以,
因为,
所以,
所以,即与互为余角;
(2)如下图,作的延长线,作的角平分线,
因为平分,
所以,
因为,
所以,
所以,即与互补;
因为,,
所以,
又因为平分,
所以.
【点睛】本题考查了余角与补角,角平分线的定义,解题的关键是掌握角平分线的定义.
18.
【分析】根据已知易得,,再根据互余的性质可得,然后利用角平分线的定义可得,即可求出的度数.
【详解】解:,,
,,
,
,
,
平分,
,
.
【点睛】本题考查了互余的性质,角平分线的定义,平角的定义,根据题意找准各角之间的数量关系是解题关键.
19.(1)
(2)
【分析】(1)先利用与的倍数关系求出的度数,然后利用余角的定义求解即可;
(2)先计算出,的度数,然后利用角平分线的定义求出的度数,最后利用角的和差关系求解即可.
【详解】(1)解:∵,,
∴,
∴的余角的度数为
(2)解:∵,,
∴,,
又平分,
∴,
∴.
【点睛】本题考查了角平分线的有关计算,余角的定义等知识,正确识图,找准角的有关关系是解题的关键.
20.(1)
(2),
【分析】(1)根据余角的定义求解即可;
(2)由已知,结合平角的定义,可得的度数,又因为与互为邻补角,可求出的度数,又由平分可求出.
【详解】(1)解:余角的度数为:
;
(2)
,,为直线,
,
.
与互补,
,
平分,
.
故可得,.
【点睛】本题主要考查了余角,邻补角的概念以及角平分线的定义,注意各角之间的关系,属于基础题,解答本题的关键是一些基本概念的掌握,难度一般.
21.(1)
(2)平分,理由见解析
【分析】(1)根据直角的性质,可得,根据补角的定义得,再由,即可求解;
(2)根据,,可得,再由,可得,从而得到,,即可求解.
【详解】(1)解:,
,
,
,
,
的度数为;
(2)解:平分,理由如下:
,,
,
,
,
,
,
,
平分.
【点睛】本题主要考查了垂直的性质,角平分线的有关计算,熟练掌握垂直的性质,根据题意得到角与角之间的数量关系是解题的关键.
22.(1)
(2)
【分析】(1)根据余角的定义,得出,再根据,计算即可得出的度数;
(2)根据角平分线的定义,得出,根据余角的定义,得出,再根据角平分线的定义,计算即可得出答案.
【详解】(1)解:∵与互为余角,
∴,
∵,
∴;
(2)解:∵是的平分线,,
∴,
∵与互为余角,
∴,
∴,
∵是的平分线,
∴.
【点睛】本题考查了与余角有关的计算、角平分线的定义,解本题的关键在理清角之间的数量关系.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
七年级数学上册 第四章 4.3.3 余角和补角 同步练习题
一、单选题
1.已知与互余,若,则( )
A. B. C. D.
2.若,则的余角是( )
A. B. C. D.
3.若,则∠A的补角为( )
A.40° B.50° C.120° D.130°
4.如果一个角的补角是,则这个角为( )
A. B. C. D.
5.一个角补角是它的余角的4倍,这个角的度数是( )
A.135° B.45° C.60° D.30°
6.下列说法中正确的个数是( )
①锐角的补角一定是钝角;②一个角的补角一定大于这个角;③已知线段,,则点P在直线外;④若,则点B为线段的中点.
A.1 B.2 C.3 D.4
7.一个角的补角比这个角的余角 倍还多,则这个角的度数为( )
A. B. C. D.
8.如图,射线表示北偏东方向,射线表示南偏西方向,则的度数是( )
A. B. C. D.
9.根据图中给定的条件,下列各图中可以判断∠1与∠2一定相等的是( )
A.①② B.①③ C.①②③ D.①②③④
10.如图所示,∠AOC与∠BOD都是直角,且∠AOB∶∠AOD=2∶11,则∠AOB=( )
A.10° B.15° C.20° D.30°
二、填空题
11.若,则的余角是 _____度.
12.若,则的补角为 .
13.已知∠1与互补,,则 °
14.如图,射线的端点O在直线上,,点D在平面内,与互余,则的度数为 .
15.如图,大家已经知道三角形三个角的和是,若.
(1)图中共有 条线段, 个小于平角的角;
(2)除三个相等的直角外,图中还有相等的角是 ;
(3)图中有 对互余的角;(4)图中有 对互补的角.
三、解答题
16.点O是直线上的点,,射线是的平分线.
(1)位置如图1时,用等式与的数量关系,并说明理由;
(2)位置如图2时,(1)中与的数量关系是否仍然成立?若成立,请说明理由;若不成立,请写出你得到的结论,并说明理由.
17.如图,已知锐角,把一个三角尺的直角顶点与点重合,一条直角边和重合,沿另一条直角边在射线的同侧画射线,再用量角器画出的平分线,此时,与互余.
(1)请你画出图形,用所学知识说明与互余;
(2)请你仿照上面互为余角的画法,在图2中画出一个,使与互补,并简要说明画图方法;若,求的度数.
18.如图,直线、相交于点O,平分,于点O,,求的度数.
19.如图,点,,在一条直线上,,平分.
(1)若,求的余角的度数.
(2)若,求的度数(用含的式子表示).
20.直线、相交于点O,平分,,,求
(1)余角的度数
(2)与的度数.
21.如图,直线、相交于点,射线在内部,且.过点作.
(1)若,求的度数;
(2)若,那么平分吗?为什么?
22.如图,与互为余角,是的平分线,是的平分线.
(1)若,求的度数;
(2)若,求的度数.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.D
【分析】根据互余的定义,即可进行解答.如果两个角相加等于,那么这两个角互余.
【详解】解:∵与互余,若,
∴,
故选:D.
【点睛】本题主要考查了互余的定义,解题的关键是掌握如果两个角相加等于,那么这两个角互余.
2.C
【分析】用即可求解.
【详解】解:,则的余角是,
故选:C.
【点睛】本题考查的是余角的定义,即如果两个角的和等于(直角),就说这两个角互为余角.即其中一个角是另一个角的余角,解题关键是掌握余角的定义.
3.D
【分析】根据互为补角的两个角的和等于列式计算即可得解.
【详解】解:的补角.
故选:D.
【点睛】本题考查了补角,熟记补角的概念是解题的关键.
4.D
【分析】根据补角的定义即可进行解答.
【详解】解:,
故选:D.
【点睛】本题主要考查了补角的定义,解题的关键是掌握“如果两个角相加等于,则这两个角互为补角”.
5.C
【分析】设这个角的度数为,则它的余角为,它的补角为,再根据一个角补角是它的余角的4倍,列出方程求解即可.
【详解】解:设这个角的度数为,则它的余角为,它的补角为,
由题意得,,
解得,
∴这个角的度数为60°,
故选C.
【点睛】本题主要考查了与余角和补角有关的计算,解题的关键在于熟知:如果两个角的度数之和为90度,那么这两个角互余;如果两个角的度数之和为180度,那么这两个角互补.
6.A
【分析】根据补角的定义,线段中点的性质,点与直线的位置关系,逐项分析判断即可求解.
【详解】解:①锐角的补角一定是钝角,故①正确;
②一个角的补角不一定大于这个角,例如角的补角等于,故②不正确;
③已知线段,,则点P在直线外或在直线上,故③不正确;
④若,且点在线段上,则点B为线段的中点,故④不正确,
故选:A.
【点睛】本题考查了补角的定义,线段中点的性质,点与直线的位置关系,掌握以上知识是解题的关键.
7.B
【分析】设这个角的度数为,根据题意列出方程,解方程即可求解.
【详解】解:设这个角的度数为,则这个角的补角为,这个角的余角为,根据题意得,
解得:,
故选:B.
【点睛】本题考查了与补角、余角相关的计算,一元一次方程的应用,根据题意列出方程是解题的关键.
8.C
【分析】先求出的余角,然后再加上与的和进行计算即可解答.
【详解】解:由题意得:
∵,
∴,
∴的度数是.
故选:C.
【点睛】本题考查方向角,余角,角的和差计算.根据题目的已知条件并结合图形分析是解题的关键.
9.A
【分析】根据同角或等角的余角相等,即可判断①和②,无法判断③和④.
【详解】解:如图①,
∵∠1+∠3=90°,∠2+∠3=90°,
∴∠1=∠2;
如图②,
∵∠1+∠3=90°,∠2+∠4=90°,∠3=∠4,
∴∠1=∠2;
如图③,无法证明∠1=∠2,
如图④,无法证明∠1=∠2,
故选:A
【点睛】此题考查了同角或等角的余角相等,熟练掌握余角的性质是解题的关键.
10.C
【分析】由∠AOB+∠BOC=∠BOC+∠COD知∠AOB=∠COD,设∠AOB=2α,则∠AOD=11α,故∠AOB+∠BOC=9α=90°,解得α,从而可求解.
【详解】解:∵∠AOC与∠BOD都是直角,
∴∠AOB+∠BOC=∠BOC+∠COD=90°,
∴∠AOB=∠COD, 设∠AOB=2α,
∵∠AOB:∠AOD=2:11,
∴
∴∠AOB+∠BOC=9α=90°,
解得α=10°,
∴∠AOB=20°.
故选:C.
【点睛】本题主要考查了几何图形中角的计算以及余角和补角,正确表示出各角度数是解题关键.
11.
【分析】利用余角的定义进行求解即可.
【详解】解:,
的余角为:.
故答案为:.
【点睛】本题主要考查余角,解答的关键是明确互为余角的两角之和为.
12./度
【分析】根据和为的两个角互为补角进行求解即可.
【详解】解:∵,
∴的补角为,
故答案为:.
【点睛】本题考查了补角的定义,熟知和为的两个角互为补角是解本题的关键.
13.108
【分析】根据和为的两个角互为补角,根据定义解答.
【详解】解:∵∠1与互补,
∴,
∵,
∴,
故答案为:.
【点睛】此题考查了补角的定义,熟记定义是解题的关键.
14.或
【分析】分两种情况讨论:①在直线上方;②在直线下方,再利用角之间的关系可以求解.
【详解】解:①当在直线上方时,如图,
∵与互余,
∴,
∴;
②当在直线的下方时,如图,
∵与互余,
∴,
∴,
∵,
∴
故答案为:或.
【点睛】本题主要考查余角与补角,解答的关键是结合图形分析清楚角与角之间的关系.
15. 6 7 , 4 3
【分析】(1)根据线段定义:直线上两个点和它们之间的部分叫做线段,写出图中线段,再写出图中小于的角即可;
(2)根据互为余角得出图中相等的角即可;
(3)根据两角相加等于的两个角互为余角,判断即可;
(4)两脚相加等于的两个角互为补角,判断即可.
【详解】解:(1)图中的线段有:,共条线段,
小于平角的角有:,共个;
(2)∵,
∴,
∵,
∴,
∴图中相等的角还有: ,;
(3)图中互余的角有:和,和,和,和,
共对;
(4)图中互补的角为:和,和,和,共对;
故答案为:6;7;,;4;3.
【点睛】本题考查了线段的定义,平角的概念,余角的概念,补角的概念等知识点,熟知定义是解决本题的关键.
16.(1);理由见解析
(2)不成立,,理由见解析
【分析】(1)由题意知,,设,则,,可得,,进而可得与的关系;
(2)同(1)分别用含的代数式表示出,,然后通过加法运算求二者的关系即可;
【详解】(1)解:,理由如下:
∵射线是的平分线,
∴,
设,则,,
∴,,
∴;
(2)解:不成立,,理由如下:
∵射线是的平分线,
∴,
设,则,,
∴,,
∵,
∴.
【点睛】本题考查了角平分线,与余角、补角有关的计算等知识.解题的关键在于明确角度之间的数量关系.
17.(1)图见解析,证明见解析
(2)图见解析,
【分析】(1)根据角平分线的定义和余角的性质即可得答案;
(2)作的延长线,作的角平分线,利用角平分线的定义和补角的性质即可得答案.
【详解】(1)解:如下图,
因为平分,
所以,
因为,
所以,
所以,即与互为余角;
(2)如下图,作的延长线,作的角平分线,
因为平分,
所以,
因为,
所以,
所以,即与互补;
因为,,
所以,
又因为平分,
所以.
【点睛】本题考查了余角与补角,角平分线的定义,解题的关键是掌握角平分线的定义.
18.
【分析】根据已知易得,,再根据互余的性质可得,然后利用角平分线的定义可得,即可求出的度数.
【详解】解:,,
,,
,
,
,
平分,
,
.
【点睛】本题考查了互余的性质,角平分线的定义,平角的定义,根据题意找准各角之间的数量关系是解题关键.
19.(1)
(2)
【分析】(1)先利用与的倍数关系求出的度数,然后利用余角的定义求解即可;
(2)先计算出,的度数,然后利用角平分线的定义求出的度数,最后利用角的和差关系求解即可.
【详解】(1)解:∵,,
∴,
∴的余角的度数为
(2)解:∵,,
∴,,
又平分,
∴,
∴.
【点睛】本题考查了角平分线的有关计算,余角的定义等知识,正确识图,找准角的有关关系是解题的关键.
20.(1)
(2),
【分析】(1)根据余角的定义求解即可;
(2)由已知,结合平角的定义,可得的度数,又因为与互为邻补角,可求出的度数,又由平分可求出.
【详解】(1)解:余角的度数为:
;
(2)
,,为直线,
,
.
与互补,
,
平分,
.
故可得,.
【点睛】本题主要考查了余角,邻补角的概念以及角平分线的定义,注意各角之间的关系,属于基础题,解答本题的关键是一些基本概念的掌握,难度一般.
21.(1)
(2)平分,理由见解析
【分析】(1)根据直角的性质,可得,根据补角的定义得,再由,即可求解;
(2)根据,,可得,再由,可得,从而得到,,即可求解.
【详解】(1)解:,
,
,
,
,
的度数为;
(2)解:平分,理由如下:
,,
,
,
,
,
,
,
平分.
【点睛】本题主要考查了垂直的性质,角平分线的有关计算,熟练掌握垂直的性质,根据题意得到角与角之间的数量关系是解题的关键.
22.(1)
(2)
【分析】(1)根据余角的定义,得出,再根据,计算即可得出的度数;
(2)根据角平分线的定义,得出,根据余角的定义,得出,再根据角平分线的定义,计算即可得出答案.
【详解】(1)解:∵与互为余角,
∴,
∵,
∴;
(2)解:∵是的平分线,,
∴,
∵与互为余角,
∴,
∴,
∵是的平分线,
∴.
【点睛】本题考查了与余角有关的计算、角平分线的定义,解本题的关键在理清角之间的数量关系.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
