数学人教A版(2019)选择性必修第一册2.1.1倾斜角与斜率 课件(共15张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.1.1倾斜角与斜率 课件(共15张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 29.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-04 22:08:50 | ||
图片预览



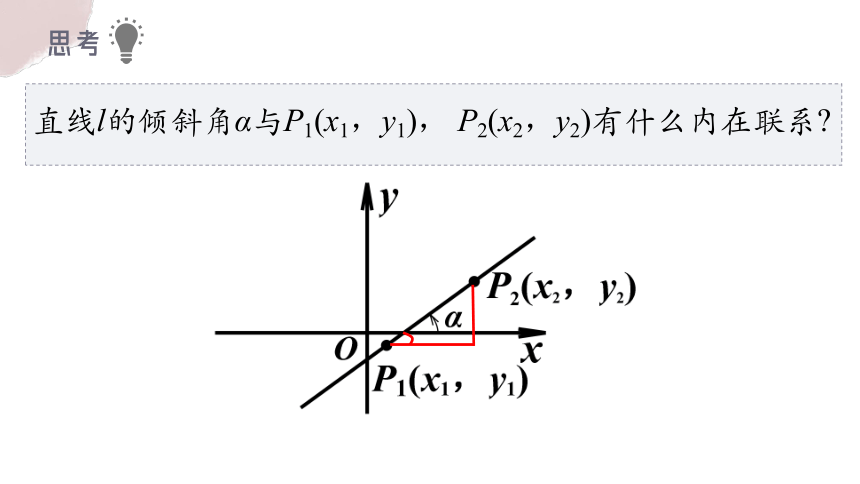
文档简介
(共15张PPT)
2.1 直线的倾斜角与斜率
2.1.1 倾斜角与斜率
LET’S START
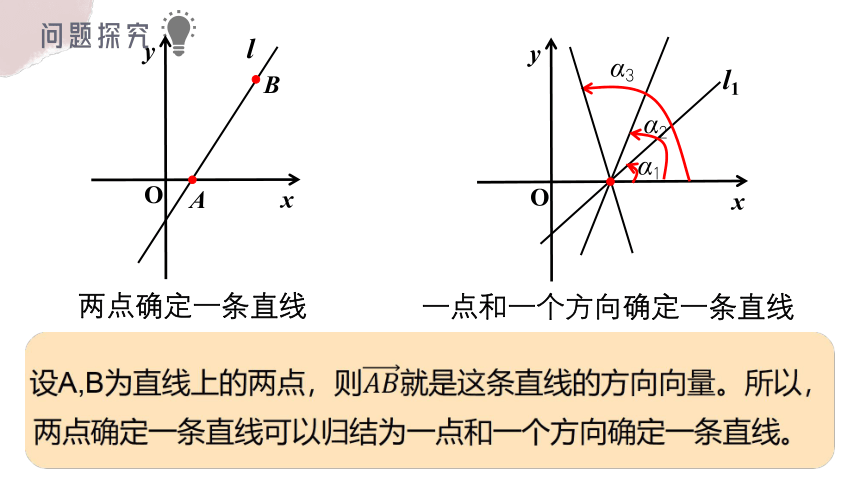
问题探究
确定一条直线的几何要素是什么?对于平面直角坐标系中的一条直线 l ,如何利用坐标系确定它的位置?
l
x
y
O
问题探究
l
x
y
O
两点确定一条直线
l1
x
y
O
α1
α2
α3
一点和一个方向确定一条直线
A
B
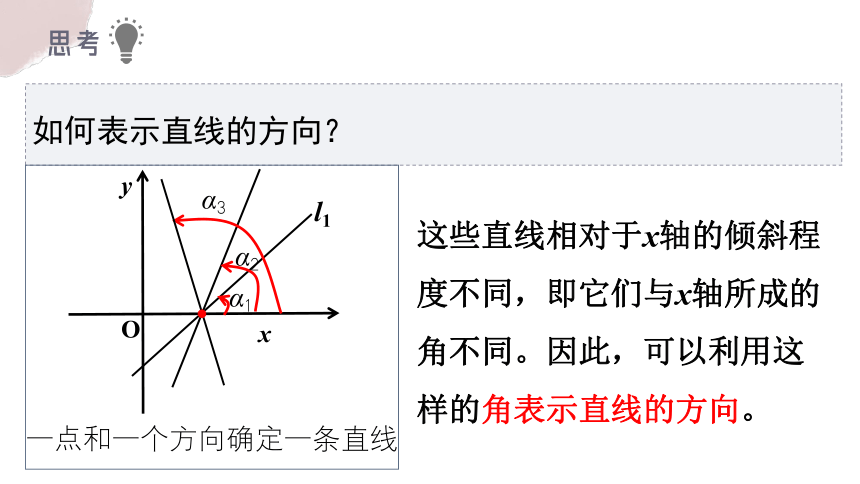
思考
如何表示直线的方向?
l1
x
y
O
α1
α2
α3
一点和一个方向确定一条直线
这些直线相对于x轴的倾斜程度不同,即它们与x轴所成的角不同。因此,可以利用这样的角表示直线的方向。
一、倾斜角
当直线 l 与 x 轴相交时,我们以 x 轴为基准,x 轴正向与直线 l 向上的方向之间所成的角 α 叫做直线的倾斜角。
l
x
y
O
α
当直线 l 与x轴平行或重合时,规定倾斜角为0°
倾斜角α 的范围:
0°≤ α <180°
思考
直线l的倾斜角α与P1(x1,y1), P2(x2,y2)有什么内在联系
探究
直线l的倾斜角α与P1(x1,y1), P2(x2,y2)有什么内在联系
探究
直线l的倾斜角α与P1(x1,y1), P2(x2,y2)有什么内在联系
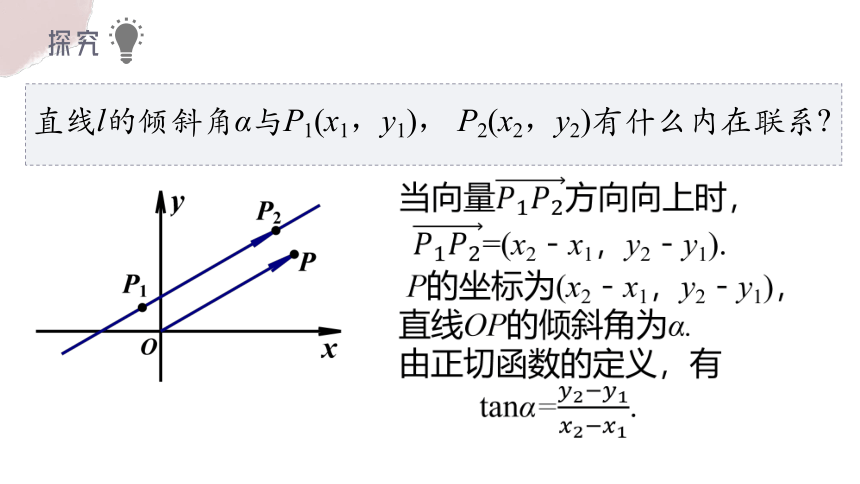
当向量向上时,
同理,可得
tanα= =.
x1 x2
探究
直线l的倾斜角α与P1(x1,y1), P2(x2,y2)有什么内在联系
x1 x2
当向量向上时,
同理,可得
tanα= =.
当x1=x2时,直线l倾斜角
为90o,上式无意义.
探究
直线l的倾斜角α与P1(x1,y1), P2(x2,y2)有什么内在联系
当直线P1P2与x轴平行或重合时,
y1=y2, α= 0o,符合tanα=
二、斜率
直线的 l 的倾斜角α与直线上的两点P1(x1,y1),P2(x2,y2),(x1≠x2)的坐标有如下关系:
我们把一条直线的倾斜角α的正切值叫做这条直线的斜率,常用小写字母k表示,即
注意:倾斜角是90°的直线没有斜率!
练习巩固
例1 如图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
练习巩固
练习1 已知下列直线的倾斜角,求直线的斜率:
(1)α=30° (2)α=45°
(3)α= (4)α=
练习巩固
练习2 已知下列直线的斜率,并判断其倾斜角是锐角还是钝角:
(1)k=0 (2)k=
(3)k= (4)k=
【答案】(1) 零角 (2)锐角
(3)钝角 (4)钝角
课堂小结
倾斜角α 的范围:
0°≤ α <180°
倾斜角α (α≠0°)的直线斜率:
直线 l 经过点A(x1,y1),B(x2,y2):
2.1 直线的倾斜角与斜率
2.1.1 倾斜角与斜率
LET’S START
问题探究
确定一条直线的几何要素是什么?对于平面直角坐标系中的一条直线 l ,如何利用坐标系确定它的位置?
l
x
y
O
问题探究
l
x
y
O
两点确定一条直线
l1
x
y
O
α1
α2
α3
一点和一个方向确定一条直线
A
B
思考
如何表示直线的方向?
l1
x
y
O
α1
α2
α3
一点和一个方向确定一条直线
这些直线相对于x轴的倾斜程度不同,即它们与x轴所成的角不同。因此,可以利用这样的角表示直线的方向。
一、倾斜角
当直线 l 与 x 轴相交时,我们以 x 轴为基准,x 轴正向与直线 l 向上的方向之间所成的角 α 叫做直线的倾斜角。
l
x
y
O
α
当直线 l 与x轴平行或重合时,规定倾斜角为0°
倾斜角α 的范围:
0°≤ α <180°
思考
直线l的倾斜角α与P1(x1,y1), P2(x2,y2)有什么内在联系
探究
直线l的倾斜角α与P1(x1,y1), P2(x2,y2)有什么内在联系
探究
直线l的倾斜角α与P1(x1,y1), P2(x2,y2)有什么内在联系
当向量向上时,
同理,可得
tanα= =.
x1 x2
探究
直线l的倾斜角α与P1(x1,y1), P2(x2,y2)有什么内在联系
x1 x2
当向量向上时,
同理,可得
tanα= =.
当x1=x2时,直线l倾斜角
为90o,上式无意义.
探究
直线l的倾斜角α与P1(x1,y1), P2(x2,y2)有什么内在联系
当直线P1P2与x轴平行或重合时,
y1=y2, α= 0o,符合tanα=
二、斜率
直线的 l 的倾斜角α与直线上的两点P1(x1,y1),P2(x2,y2),(x1≠x2)的坐标有如下关系:
我们把一条直线的倾斜角α的正切值叫做这条直线的斜率,常用小写字母k表示,即
注意:倾斜角是90°的直线没有斜率!
练习巩固
例1 如图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
练习巩固
练习1 已知下列直线的倾斜角,求直线的斜率:
(1)α=30° (2)α=45°
(3)α= (4)α=
练习巩固
练习2 已知下列直线的斜率,并判断其倾斜角是锐角还是钝角:
(1)k=0 (2)k=
(3)k= (4)k=
【答案】(1) 零角 (2)锐角
(3)钝角 (4)钝角
课堂小结
倾斜角α 的范围:
0°≤ α <180°
倾斜角α (α≠0°)的直线斜率:
直线 l 经过点A(x1,y1),B(x2,y2):
