八年级数学上册试题 12.1 函数-沪科版(含答案)
文档属性
| 名称 | 八年级数学上册试题 12.1 函数-沪科版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 208.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-05 19:35:56 | ||
图片预览




文档简介
12.1 函数
第1课时
一、单选题
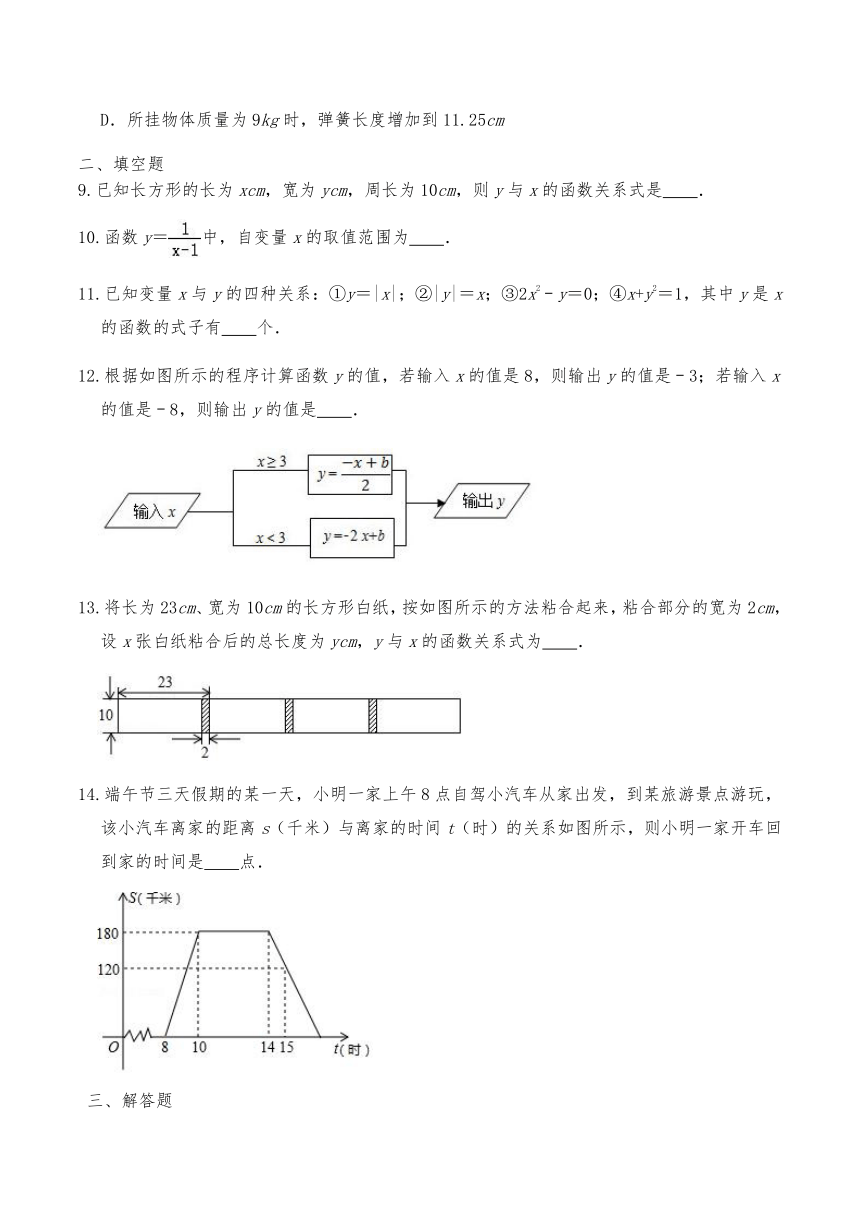
1.下列图形中,不能代表y是x函数的是( )
A. B.
C. D.
2.将水匀速滴进如图所示的容器时,能正确反映容器中水的高度(h)与时间(t)之间对应关系的图象大致是( )
A. B.
C. D.
3.函数y=自变量的取值范围是( )
A.x≠2020 B.x≠﹣2020 C.x≠2021 D.x≠﹣2021
4.某通讯公司推出三种上网月收费方式.这三种收费方式每月所收的费用y(元)与上网时间x(小时)的函数关系如图所示,则下列判断错误的是( )
A.每月上网不足25小时,选择A方式最省钱
B.每月上网时间为30小时,选择B方式最省钱
C.每月上网费用为60元,选择B方式比A方式时间长
D.每月上网时间超过70小时,选择C方式最省钱
5.“脱贫攻坚”小组乘汽车赴360km处的农村进行调研,前一段路为高速公路,后段路为乡村公路,汽车在高速公路和乡村公路上分别以某一速度高速行驶,汽车行驶的路程y(km)与时间x(h)间的关系如图所示,则该记者到达采访地的时间为( )
A.4小时 B.4.5小时 C.5小时 D.5.5小时
6.已知小明从A地到B地,速度为4千米/小时,A、B两地相距3千米,若用x(小时)表示行走的时间,y(千米)表示余下的路程,则y与x之间的函数表达式是( )
A.y=4x B.y=4x﹣3 C.y=﹣4x D.y=﹣4x+3
7.变量x,y的一些对应值如下表:
x … ﹣2 ﹣1 0 1 2 3 …
y … ﹣8 ﹣1 0 1 8 27 …
根据表格中的数据规律,当x=﹣5时,y的值是( )
A.75 B.﹣75 C.125 D.﹣125
8.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x(kg)间有下面的关系(弹簧的弹性范围x≤10kg);
x 0 2 4 6 8 10
y 10 10.5 11 11.5 12 12.5
下列说法不正确的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂重物时的长度为10cm
C.所挂物体质量为5kg时,弹簧长度增加了1.25cm
D.所挂物体质量为9kg时,弹簧长度增加到11.25cm
二、填空题
9.已知长方形的长为xcm,宽为ycm,周长为10cm,则y与x的函数关系式是 .
10.函数y=中,自变量x的取值范围为 .
11.已知变量x与y的四种关系:①y=|x|;②|y|=x;③2x2﹣y=0;④x+y2=1,其中y是x的函数的式子有 个.
12.根据如图所示的程序计算函数y的值,若输入x的值是8,则输出y的值是﹣3;若输入x的值是﹣8,则输出y的值是 .
13.将长为23cm、宽为10cm的长方形白纸,按如图所示的方法粘合起来,粘合部分的宽为2cm,设x张白纸粘合后的总长度为ycm,y与x的函数关系式为 .
14.端午节三天假期的某一天,小明一家上午8点自驾小汽车从家出发,到某旅游景点游玩,该小汽车离家的距离s(千米)与离家的时间t(时)的关系如图所示,则小明一家开车回到家的时间是 点.
三、解答题
15.某地区一天的气温变化较大,如图表示该地区一天24小时的气温变化情况.
(1)如图描述的两个变量中自变量是什么?因变量是什么?
(2)一天中哪个时间气温最高、哪个时间最低,最高最低气温分别是多少?
(3)在什么时间范围内气温上升?
(4)该地区一天的温差是多少?
16.琳琳通过新闻了解到,近来意大利“新冠肺炎”疫情愈发严重,决定给意大利的网友Carlo邮寄一批防疫用品.已知琳琳家、药店、邮局在同一直线上,琳琳从家出发,跑步去药店买了酒精和口罩,又步行到邮局把物品寄出,然后再走回家.琳琳离家的距离y与时间x之间的关系如图所示,请根据图象解决下列问题:
(1)琳琳家离药店的距离为 km.
(2)琳琳邮寄物品用了 min.
(3)琳琳两段步行的速度分别是多少?
(4)图中点P的意义是 .
17.一个函数的图象如图所示,根据图象回答问题
(1)写出自变量x的取值范围;
(2)当x=18时,则y的值是 ;
(3)求△ABO的面积;
(4)当18≤x<23时,请说明:当x的值逐渐变大时,函数值y怎样变化?
18.由于持续高温和连日无雨,某水库的蓄水量随着时间的增加而减少.蓄水量y(万立方米)与干旱时间t(天)之间的关系如图所示,回答下列问题:
(1)干旱持续到第10天,水库的蓄水量为 万立方米.
(2)若水库的蓄水量小于360万立方米时,将发生严重干旱警报,那么多少天后将发生严重干旱警报?
(3)在(2)的条件下,照这样干旱下去,预计再持续多少天时,水库将干涸.
19.如图是小李骑自行车离家的距离s(km)与时间t(h)之间的关系.
(1)在这个变化过程中自变量 ,因变量是 ;
(2)小李 时到达离家最远的地方?此时离家 km;
(3)分别写出在1<t<2时和2<t<4时小李骑自行车的速度为 km/h和 km/h.
(4)小李 时与家相距20km.
20.如图为小强在早晨8时从城市出发到郊外所走的路程与时间的变化图.根据图回答问题:
(1)图象中自变量是 ,因变量是 ;
(2)9时,10时30分,12时小强所走的路程分别是 千米, 千米, 千米;
(3)小强休息了多长时间: 小时;
(4)求小强从休息后直至到达目的地这段时间的平均速度.
第2课时
一.选择题
1.函数y=中自变量x的取值范围是( )
A.x≥﹣2且x≠1 B.x≥﹣2 C.x≠1 D.﹣2≤x<1
2.函数y=﹣中,自变量x的取值范围是( )
A.x≤ B.x≥ C.x<且x≠﹣1 D.x≤且x≠﹣1
3.已知A、B两地相距3千米,小黄从A地到B地,平均速度为4千米/小时,若用x表示行走的时间(小时),y表示余下的路程(千米),则y关于x的函数解析式是( )
A.y=4x(x≥0) B.y=4x﹣3(x≥)
C.y=3﹣4x(x≥0) D.y=3﹣4x(0≤x≤)
4.根据如图所示的程序计算函数y的值,若输入x的值是7,则输出y的值是﹣2,若输入x的值是﹣8,则输出y的值是( )
A.5 B.10 C.19 D.21
5.下表是摄氏温度和华氏温度之间的对应表,则字母a的值是( )
华氏°F 23 32 41 a 59
摄氏°C ﹣5 0 5 10 15
A.45 B.50 C.53 D.68
6.下列各曲线中哪个不能表示y是x的函数的是( )
A. B.
C. D.
7.函数中自变量x的取值范围是( )
A.x≥3 B.x≤7 C.3≤x≤7 D.x≤3或x≥7
8.某地区2019年元月份的国民生产总值为a万元,2月份比元月份减少5%,3月份预计比2月份增加了9%,若该地区2019年3月份的国民生产总值为b万元,则a、b之间的关系为( )
A.b=(a﹣5%)(a+9%) B.b=(a﹣5%+9%)
C.b=a(1﹣5%+9%) D.b=a(1﹣5%)(1+9%)
9.下列关系式中,y不是自变量x的函数的是( )
A.y=x B.y=x2 C.y=|x| D.y2=x
10.某函数图象如图所示,则该函数解析式可能为( )
A.y=﹣ B.y= C.y=﹣ D.y=
二.填空题
11.在函数y=中,自变量x的取值范围是 .
12.在登山过程中,海拔每升高1千米,气温下降6℃,已知某登山大本营所在的位置的气温是2℃,登山队员从大本营出发登山,当海拔升高x千米时,所在位置的气温是y℃,那么y关于x的函数解析式是 .
13.已知f(x)=x2﹣1,那么f(﹣1)= .
14.函数y=+中自变量x的取值范围是 .
15.函数y=|x﹣1|+2|x﹣2|+3|x﹣3|+4|x﹣4|的最小值是 .
16.函数y=中,自变量x的取值范围为 .
17.某商人购货,进价已按原价a扣去25%,他希望对货物订一新价格,以便按新价让利20%销售后仍可获得25%的利润,则此商人经营这种货物的件数x与按新价让利总额y之间的函数关系式为 .
18.a是一个正实数,记f(x)=,其中[x]是不超过实数x的最大整数,如[2.1]=2,[﹣2.1]=﹣3,若f(5)=5,则a的取值范围是 .
三.解答题
19.已知f(x)=,其中f(a)表示当x=a时对应的函数值,如:
f(1)=;
f(2)=;
f(3)=;
f(a)=.
请根据该函数反映出的规律解决下列问题
(1)求f(1)+f(2)+f(3)+…+f()的值;
(2)猜想:f(n)+f(n+1)= .
20.已知y是x的函数,x的取值范围为任意实数,如图是x与y的几组对应值,小华同学根据研究函数的已有经验探索这个函数的有关性质,并完成下列问题.
x … ﹣3 ﹣2 ﹣1 0 1 2 3 …
y … 3 2 1 0 1 2 3 …
(1)如图,小华在平面直角坐标系中描出了上述几组值对应的点,请你根据描出的点画出函数的图象;
(2)请根据你画出的函数图象,完成
①当x=﹣4时,求y的值;
②当2012≤|y|≤2019时,求x的取值范围.
第1课时答案
一、单选题
C. D.C.B.C.D.D.D.
二、填空题
9.y=5﹣x.
10.x≠1.
11.2.
12.18.
13.y=21x+2.
14.17.
三、解答题
15.解:(1)由图象可知,时间是自变量,气温是因变量;
(2)一天中0时和24时的气温最低,是5℃;15时的气温最高,是40℃;
(3)在0≤t<6和9≤t<15时,气温上升;
(4)该地区一天的温差是:40﹣5=35(℃).
16.解:(1)由图象可知,琳琳家离药店的距离为2.5km.
故答案为:2.5;
(2)由图象可知,琳琳邮寄物品用了:65﹣45=20(分钟),
故答案为:20;
(3)从药店步行到邮局的路程为1km,时间为15min,所以速度为km/min;
从邮局步行回家的路程为1.5km,时间为25min,所以速度为:(km/min);
(4)图中点P的意义是:离家45min时,琳琳到达邮局,此时她离家的距离为1.5km.
故答案为:离家45min时,琳琳到达邮局,此时她离家的距离为1.5km.
17.解:(1)自变量x的取值范围是0≤x≤23;
(2)当x=18时,则y的值是 12;
故答案为:12;
(3);
(4)由图象可知,当18≤x<23时,当x的值逐渐变大时,函数值y随着x的变大而减小.
18.解:(1)由图象可知,干旱持续到第10天,水库的蓄水量为1200万立方米.
故答案为:1200;
(2)(1500﹣1200)÷10=30(万立方米),
(1500﹣360)÷30=38(天),
答:38天后将发生严重干旱警报;
(3)1500÷30﹣38=12(天),
答:照这样干旱下去,预计再持续12天时,水库将干涸.
19.解:(1)根据图象可知,在这个变化过程中自变量是离家时间,因变量是离家距离;
(2)根据图象可知小李2h后到达离家最远的地方,此时离家30km;
(3)当1<t<2时,小李行进的距离为30﹣10=20(km),用时2﹣1=1(h),
所以小李在这段时间的速度为:(km/h),
当2<t<4时,小李行进的距离为30﹣20=10(km),用时4﹣2=2(h),
所以小李在这段时间的速度为:(km/h);
(4)根据图象可知:小李h或4h与家相距20km.
故答案为:(1)离家时间;离家距离;(2)2;30;(3)20;5;(4)h或4h.
20.解:(1)时间,路程;
(2)4,9,15;
(3)0.5;
(4)平均速度为:(15﹣9)÷(12﹣10.5)=4(千米/时),
答:小强从休息后直至到达目的地的平均速度为4千米/时.
故答案为:(1)时间,路程;
(2)4,9,15;
(3)0.5;
(4)4千米/时.
第2课时答案
一.选择题
A.D.D.C.B.D.C.D.D.D.
二.填空题
11.x≤且x≠0.
12.y=﹣6x+2.
13.0.
14.x≥1且x≠2.
15.8.
16.x>1或x<﹣1.
17.y=x.
18.25≤a<35.
三.解答题
19.解:(1)f(1)+f(2)+f(3)+…+f()=1﹣+﹣+﹣+…+﹣+=1﹣=;
(2)f(n)+f(n+1)=+=﹣+﹣=.
故答案为:.
20.解:
(1)由表格的数据所画的图象如图所示:
(2)①由图象可知,函数解析式为:y=|x|
∴当x=﹣4时,求y=4
②由2012≤|y|≤2019,可得﹣2019≤y≤﹣2012或2012≤y≤2019
故所得的x的取值范围为:﹣2019≤x≤﹣2012和2012≤x≤2019
第1课时
一、单选题
1.下列图形中,不能代表y是x函数的是( )
A. B.
C. D.
2.将水匀速滴进如图所示的容器时,能正确反映容器中水的高度(h)与时间(t)之间对应关系的图象大致是( )
A. B.
C. D.
3.函数y=自变量的取值范围是( )
A.x≠2020 B.x≠﹣2020 C.x≠2021 D.x≠﹣2021
4.某通讯公司推出三种上网月收费方式.这三种收费方式每月所收的费用y(元)与上网时间x(小时)的函数关系如图所示,则下列判断错误的是( )
A.每月上网不足25小时,选择A方式最省钱
B.每月上网时间为30小时,选择B方式最省钱
C.每月上网费用为60元,选择B方式比A方式时间长
D.每月上网时间超过70小时,选择C方式最省钱
5.“脱贫攻坚”小组乘汽车赴360km处的农村进行调研,前一段路为高速公路,后段路为乡村公路,汽车在高速公路和乡村公路上分别以某一速度高速行驶,汽车行驶的路程y(km)与时间x(h)间的关系如图所示,则该记者到达采访地的时间为( )
A.4小时 B.4.5小时 C.5小时 D.5.5小时
6.已知小明从A地到B地,速度为4千米/小时,A、B两地相距3千米,若用x(小时)表示行走的时间,y(千米)表示余下的路程,则y与x之间的函数表达式是( )
A.y=4x B.y=4x﹣3 C.y=﹣4x D.y=﹣4x+3
7.变量x,y的一些对应值如下表:
x … ﹣2 ﹣1 0 1 2 3 …
y … ﹣8 ﹣1 0 1 8 27 …
根据表格中的数据规律,当x=﹣5时,y的值是( )
A.75 B.﹣75 C.125 D.﹣125
8.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x(kg)间有下面的关系(弹簧的弹性范围x≤10kg);
x 0 2 4 6 8 10
y 10 10.5 11 11.5 12 12.5
下列说法不正确的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂重物时的长度为10cm
C.所挂物体质量为5kg时,弹簧长度增加了1.25cm
D.所挂物体质量为9kg时,弹簧长度增加到11.25cm
二、填空题
9.已知长方形的长为xcm,宽为ycm,周长为10cm,则y与x的函数关系式是 .
10.函数y=中,自变量x的取值范围为 .
11.已知变量x与y的四种关系:①y=|x|;②|y|=x;③2x2﹣y=0;④x+y2=1,其中y是x的函数的式子有 个.
12.根据如图所示的程序计算函数y的值,若输入x的值是8,则输出y的值是﹣3;若输入x的值是﹣8,则输出y的值是 .
13.将长为23cm、宽为10cm的长方形白纸,按如图所示的方法粘合起来,粘合部分的宽为2cm,设x张白纸粘合后的总长度为ycm,y与x的函数关系式为 .
14.端午节三天假期的某一天,小明一家上午8点自驾小汽车从家出发,到某旅游景点游玩,该小汽车离家的距离s(千米)与离家的时间t(时)的关系如图所示,则小明一家开车回到家的时间是 点.
三、解答题
15.某地区一天的气温变化较大,如图表示该地区一天24小时的气温变化情况.
(1)如图描述的两个变量中自变量是什么?因变量是什么?
(2)一天中哪个时间气温最高、哪个时间最低,最高最低气温分别是多少?
(3)在什么时间范围内气温上升?
(4)该地区一天的温差是多少?
16.琳琳通过新闻了解到,近来意大利“新冠肺炎”疫情愈发严重,决定给意大利的网友Carlo邮寄一批防疫用品.已知琳琳家、药店、邮局在同一直线上,琳琳从家出发,跑步去药店买了酒精和口罩,又步行到邮局把物品寄出,然后再走回家.琳琳离家的距离y与时间x之间的关系如图所示,请根据图象解决下列问题:
(1)琳琳家离药店的距离为 km.
(2)琳琳邮寄物品用了 min.
(3)琳琳两段步行的速度分别是多少?
(4)图中点P的意义是 .
17.一个函数的图象如图所示,根据图象回答问题
(1)写出自变量x的取值范围;
(2)当x=18时,则y的值是 ;
(3)求△ABO的面积;
(4)当18≤x<23时,请说明:当x的值逐渐变大时,函数值y怎样变化?
18.由于持续高温和连日无雨,某水库的蓄水量随着时间的增加而减少.蓄水量y(万立方米)与干旱时间t(天)之间的关系如图所示,回答下列问题:
(1)干旱持续到第10天,水库的蓄水量为 万立方米.
(2)若水库的蓄水量小于360万立方米时,将发生严重干旱警报,那么多少天后将发生严重干旱警报?
(3)在(2)的条件下,照这样干旱下去,预计再持续多少天时,水库将干涸.
19.如图是小李骑自行车离家的距离s(km)与时间t(h)之间的关系.
(1)在这个变化过程中自变量 ,因变量是 ;
(2)小李 时到达离家最远的地方?此时离家 km;
(3)分别写出在1<t<2时和2<t<4时小李骑自行车的速度为 km/h和 km/h.
(4)小李 时与家相距20km.
20.如图为小强在早晨8时从城市出发到郊外所走的路程与时间的变化图.根据图回答问题:
(1)图象中自变量是 ,因变量是 ;
(2)9时,10时30分,12时小强所走的路程分别是 千米, 千米, 千米;
(3)小强休息了多长时间: 小时;
(4)求小强从休息后直至到达目的地这段时间的平均速度.
第2课时
一.选择题
1.函数y=中自变量x的取值范围是( )
A.x≥﹣2且x≠1 B.x≥﹣2 C.x≠1 D.﹣2≤x<1
2.函数y=﹣中,自变量x的取值范围是( )
A.x≤ B.x≥ C.x<且x≠﹣1 D.x≤且x≠﹣1
3.已知A、B两地相距3千米,小黄从A地到B地,平均速度为4千米/小时,若用x表示行走的时间(小时),y表示余下的路程(千米),则y关于x的函数解析式是( )
A.y=4x(x≥0) B.y=4x﹣3(x≥)
C.y=3﹣4x(x≥0) D.y=3﹣4x(0≤x≤)
4.根据如图所示的程序计算函数y的值,若输入x的值是7,则输出y的值是﹣2,若输入x的值是﹣8,则输出y的值是( )
A.5 B.10 C.19 D.21
5.下表是摄氏温度和华氏温度之间的对应表,则字母a的值是( )
华氏°F 23 32 41 a 59
摄氏°C ﹣5 0 5 10 15
A.45 B.50 C.53 D.68
6.下列各曲线中哪个不能表示y是x的函数的是( )
A. B.
C. D.
7.函数中自变量x的取值范围是( )
A.x≥3 B.x≤7 C.3≤x≤7 D.x≤3或x≥7
8.某地区2019年元月份的国民生产总值为a万元,2月份比元月份减少5%,3月份预计比2月份增加了9%,若该地区2019年3月份的国民生产总值为b万元,则a、b之间的关系为( )
A.b=(a﹣5%)(a+9%) B.b=(a﹣5%+9%)
C.b=a(1﹣5%+9%) D.b=a(1﹣5%)(1+9%)
9.下列关系式中,y不是自变量x的函数的是( )
A.y=x B.y=x2 C.y=|x| D.y2=x
10.某函数图象如图所示,则该函数解析式可能为( )
A.y=﹣ B.y= C.y=﹣ D.y=
二.填空题
11.在函数y=中,自变量x的取值范围是 .
12.在登山过程中,海拔每升高1千米,气温下降6℃,已知某登山大本营所在的位置的气温是2℃,登山队员从大本营出发登山,当海拔升高x千米时,所在位置的气温是y℃,那么y关于x的函数解析式是 .
13.已知f(x)=x2﹣1,那么f(﹣1)= .
14.函数y=+中自变量x的取值范围是 .
15.函数y=|x﹣1|+2|x﹣2|+3|x﹣3|+4|x﹣4|的最小值是 .
16.函数y=中,自变量x的取值范围为 .
17.某商人购货,进价已按原价a扣去25%,他希望对货物订一新价格,以便按新价让利20%销售后仍可获得25%的利润,则此商人经营这种货物的件数x与按新价让利总额y之间的函数关系式为 .
18.a是一个正实数,记f(x)=,其中[x]是不超过实数x的最大整数,如[2.1]=2,[﹣2.1]=﹣3,若f(5)=5,则a的取值范围是 .
三.解答题
19.已知f(x)=,其中f(a)表示当x=a时对应的函数值,如:
f(1)=;
f(2)=;
f(3)=;
f(a)=.
请根据该函数反映出的规律解决下列问题
(1)求f(1)+f(2)+f(3)+…+f()的值;
(2)猜想:f(n)+f(n+1)= .
20.已知y是x的函数,x的取值范围为任意实数,如图是x与y的几组对应值,小华同学根据研究函数的已有经验探索这个函数的有关性质,并完成下列问题.
x … ﹣3 ﹣2 ﹣1 0 1 2 3 …
y … 3 2 1 0 1 2 3 …
(1)如图,小华在平面直角坐标系中描出了上述几组值对应的点,请你根据描出的点画出函数的图象;
(2)请根据你画出的函数图象,完成
①当x=﹣4时,求y的值;
②当2012≤|y|≤2019时,求x的取值范围.
第1课时答案
一、单选题
C. D.C.B.C.D.D.D.
二、填空题
9.y=5﹣x.
10.x≠1.
11.2.
12.18.
13.y=21x+2.
14.17.
三、解答题
15.解:(1)由图象可知,时间是自变量,气温是因变量;
(2)一天中0时和24时的气温最低,是5℃;15时的气温最高,是40℃;
(3)在0≤t<6和9≤t<15时,气温上升;
(4)该地区一天的温差是:40﹣5=35(℃).
16.解:(1)由图象可知,琳琳家离药店的距离为2.5km.
故答案为:2.5;
(2)由图象可知,琳琳邮寄物品用了:65﹣45=20(分钟),
故答案为:20;
(3)从药店步行到邮局的路程为1km,时间为15min,所以速度为km/min;
从邮局步行回家的路程为1.5km,时间为25min,所以速度为:(km/min);
(4)图中点P的意义是:离家45min时,琳琳到达邮局,此时她离家的距离为1.5km.
故答案为:离家45min时,琳琳到达邮局,此时她离家的距离为1.5km.
17.解:(1)自变量x的取值范围是0≤x≤23;
(2)当x=18时,则y的值是 12;
故答案为:12;
(3);
(4)由图象可知,当18≤x<23时,当x的值逐渐变大时,函数值y随着x的变大而减小.
18.解:(1)由图象可知,干旱持续到第10天,水库的蓄水量为1200万立方米.
故答案为:1200;
(2)(1500﹣1200)÷10=30(万立方米),
(1500﹣360)÷30=38(天),
答:38天后将发生严重干旱警报;
(3)1500÷30﹣38=12(天),
答:照这样干旱下去,预计再持续12天时,水库将干涸.
19.解:(1)根据图象可知,在这个变化过程中自变量是离家时间,因变量是离家距离;
(2)根据图象可知小李2h后到达离家最远的地方,此时离家30km;
(3)当1<t<2时,小李行进的距离为30﹣10=20(km),用时2﹣1=1(h),
所以小李在这段时间的速度为:(km/h),
当2<t<4时,小李行进的距离为30﹣20=10(km),用时4﹣2=2(h),
所以小李在这段时间的速度为:(km/h);
(4)根据图象可知:小李h或4h与家相距20km.
故答案为:(1)离家时间;离家距离;(2)2;30;(3)20;5;(4)h或4h.
20.解:(1)时间,路程;
(2)4,9,15;
(3)0.5;
(4)平均速度为:(15﹣9)÷(12﹣10.5)=4(千米/时),
答:小强从休息后直至到达目的地的平均速度为4千米/时.
故答案为:(1)时间,路程;
(2)4,9,15;
(3)0.5;
(4)4千米/时.
第2课时答案
一.选择题
A.D.D.C.B.D.C.D.D.D.
二.填空题
11.x≤且x≠0.
12.y=﹣6x+2.
13.0.
14.x≥1且x≠2.
15.8.
16.x>1或x<﹣1.
17.y=x.
18.25≤a<35.
三.解答题
19.解:(1)f(1)+f(2)+f(3)+…+f()=1﹣+﹣+﹣+…+﹣+=1﹣=;
(2)f(n)+f(n+1)=+=﹣+﹣=.
故答案为:.
20.解:
(1)由表格的数据所画的图象如图所示:
(2)①由图象可知,函数解析式为:y=|x|
∴当x=﹣4时,求y=4
②由2012≤|y|≤2019,可得﹣2019≤y≤﹣2012或2012≤y≤2019
故所得的x的取值范围为:﹣2019≤x≤﹣2012和2012≤x≤2019
