八年级数学上册试题 15.1.1 平面直角坐标系中的轴对称-沪科版(含答案)
文档属性
| 名称 | 八年级数学上册试题 15.1.1 平面直角坐标系中的轴对称-沪科版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 559.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-05 00:00:00 | ||
图片预览


文档简介
15.1.1 平面直角坐标系中的轴对称
一、单选题
1.点P(-3,1)关于x轴对称的点的坐标是( )
A.(﹣3,1) B.(﹣3,﹣1) C.(1,﹣3) D.(3,1)
2.已知点与点关于轴对称,那么点的坐标为( )
A. B. C. D.
3.如图,在等腰△ABO中,∠ABO=90°,腰长为2,则A点关于x轴的对称点的坐标为( )
A.(-2,2) B.(-2,-2) C.(2,2) D.(2,-2)
4.如图,与关于直线对称,若, ,则度数为( )
A. B. C. D.
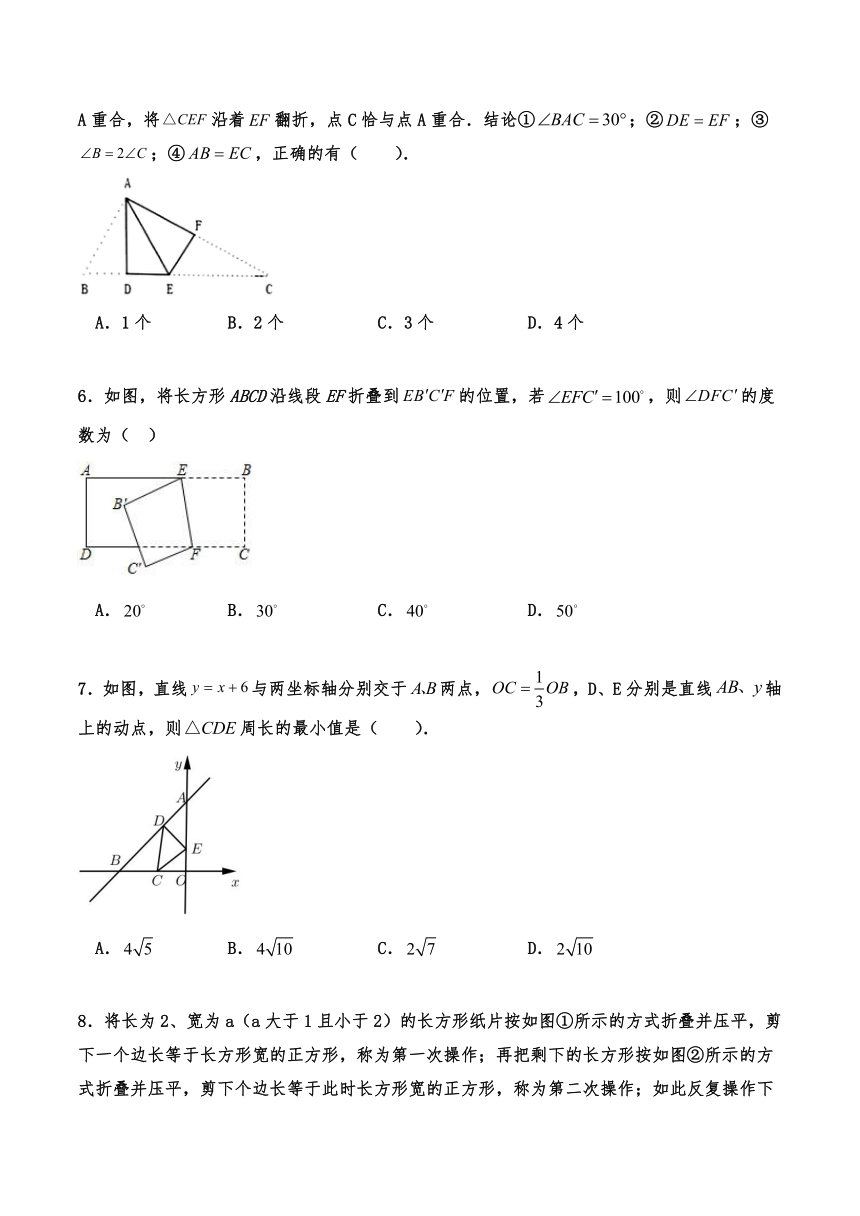
5.在中,点D,E在边上,点F在边上,将沿着翻折,点C恰与点A重合,将沿着翻折,点C恰与点A重合.结论①;②;③;④,正确的有( ).
A.1个 B.2个 C.3个 D.4个
6.如图,将长方形ABCD沿线段EF折叠到的位置,若,则的度数为( )
A. B. C. D.
7.如图,直线与两坐标轴分别交于两点,,D、E分别是直线轴上的动点,则周长的最小值是( ).
A. B. C. D.
8.将长为2、宽为a(a大于1且小于2)的长方形纸片按如图①所示的方式折叠并压平,剪下一个边长等于长方形宽的正方形,称为第一次操作;再把剩下的长方形按如图②所示的方式折叠并压平,剪下个边长等于此时长方形宽的正方形,称为第二次操作;如此反复操作下去…,若在第n次操作后,剩下的长方形恰为正方形,则操作终止.当n=3时,a的值为( )
A.1.8或1.5 B.1.5或1.2 C.1.5 D.1.2
二、填空题
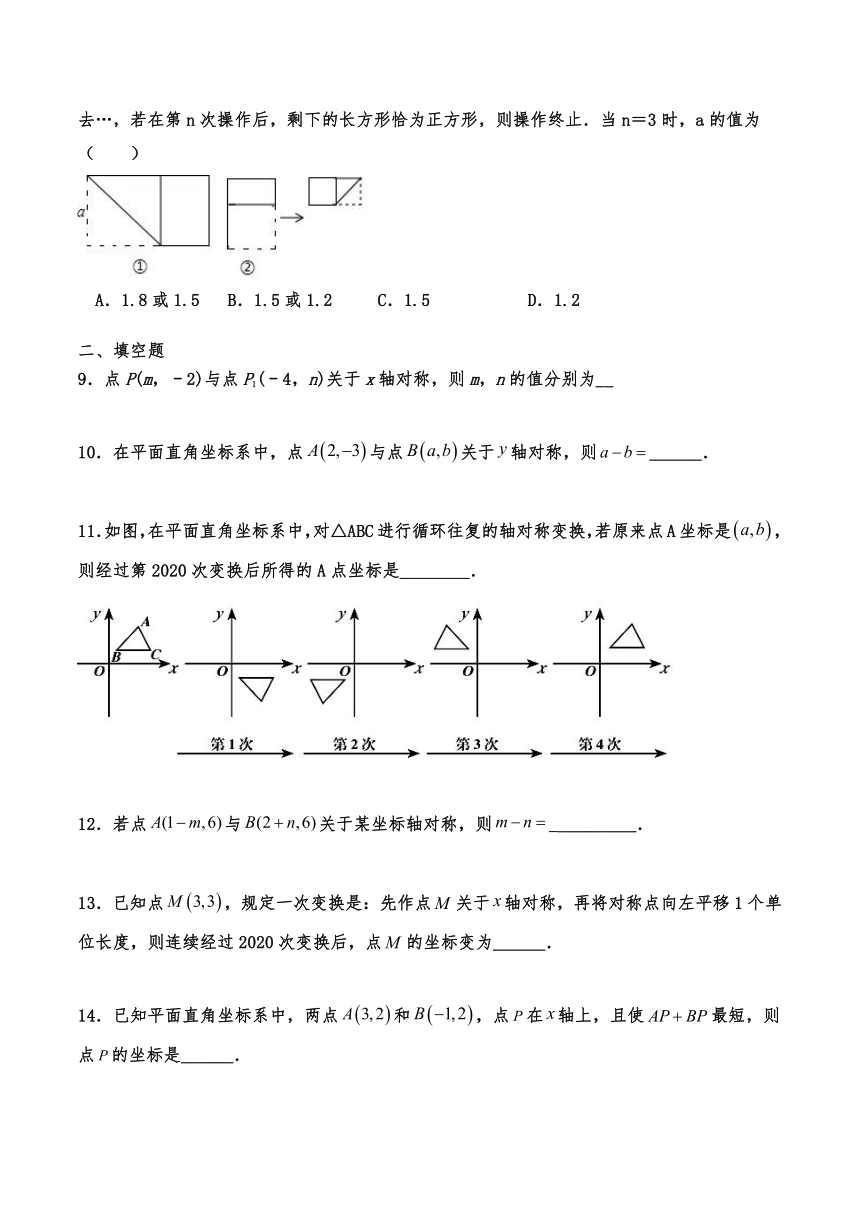
9.点P(m,﹣2)与点P1(﹣4,n)关于x轴对称,则m,n的值分别为__
10.在平面直角坐标系中,点与点关于轴对称,则______.
11.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A坐标是,则经过第2020次变换后所得的A点坐标是________.
12.若点与关于某坐标轴对称,则 _________.
13.已知点,规定一次变换是:先作点关于轴对称,再将对称点向左平移1个单位长度,则连续经过2020次变换后,点的坐标变为______.
14.已知平面直角坐标系中,两点和,点在轴上,且使最短,则点的坐标是______.
三、解答题
15.如图,在平面直角坐标系中,已知△ABC.
(1)将△ABC向下平移6个单位,得△A1B1C1,画出△A1B1C1;
(2)画出△ABC关于y轴的对称图形△A2B2C2;
(3)并直接写出△ABC的面积.
16.如图,在平面直角坐标系中,.
(1)在图中作出关于轴对称的;
(2)的面积为______.
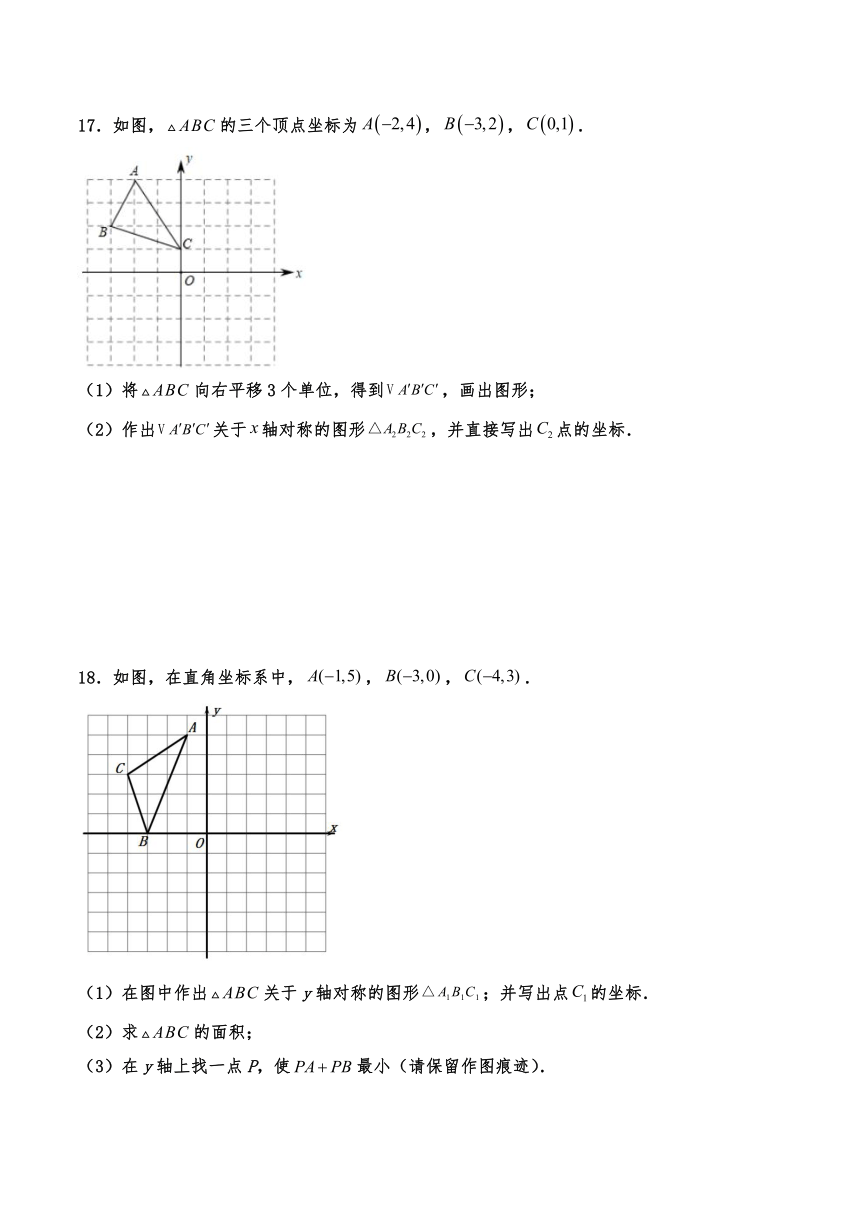
17.如图,的三个顶点坐标为,,.
(1)将向右平移3个单位,得到,画出图形;
(2)作出关于轴对称的图形,并直接写出点的坐标.
18.如图,在直角坐标系中,,,.
(1)在图中作出关于y轴对称的图形;并写出点的坐标.
(2)求的面积;
(3)在y轴上找一点P,使最小(请保留作图痕迹).
19.在平面直角坐标系中的位置如图所示.,,三点在格点上.
(1)作出关于轴对称的,并写出点的坐标______;
(2)在轴上找点,使得最小,作出点并写出点的坐标______(不用圆规,直尺就行);
(3)求的面积.
20.作图题(不写作法,保留作图痕迹,画出路径即可)
(1)请你设计一条路径,使得球P撞击台球桌边反射后,撞到球Q;
(2)请你设计一条路径,使得球P依次撞击台球桌边反射后,撞到球Q.
答案
一、单选题
B.D.B.A.B.A.A.B.
二、填空题
9.m=﹣4,n=2.
10.1.
11.(a,b).
12.3.
13.( 2017,3).
14.(1,0).
三、解答题
15.
解:(1)如图所示,△A1B1C1即为所求;
(2)如图所示,△A2B2C2即为所求;
(3)△ABC的面积为:3×4﹣×2×3﹣×2×2﹣×1×4=12﹣3﹣2﹣2=5.
16.
(1)如图所示:即为所求;
(2).
17.
解:如图所示,即为所求;
如图所示,即为所求,点的坐标为.
18.
(1)如图,为所作;点C1的坐标为(4,3);
(2)△ABC的面积=3×5 ×3×1 ×3×2 ×5×2=;
(3)如图,P点为所求.
.
19.
(1)作图如下,写出坐标
故答案为:;
(2)作图如下,写出坐标
故答案为:;
(3).
20.
解:(1)如图,运动路径:P→M→Q,点M即为所求.
(2)如图,运动路径:P→E→F→Q,点E,点F即为所求.
一、单选题
1.点P(-3,1)关于x轴对称的点的坐标是( )
A.(﹣3,1) B.(﹣3,﹣1) C.(1,﹣3) D.(3,1)
2.已知点与点关于轴对称,那么点的坐标为( )
A. B. C. D.
3.如图,在等腰△ABO中,∠ABO=90°,腰长为2,则A点关于x轴的对称点的坐标为( )
A.(-2,2) B.(-2,-2) C.(2,2) D.(2,-2)
4.如图,与关于直线对称,若, ,则度数为( )
A. B. C. D.
5.在中,点D,E在边上,点F在边上,将沿着翻折,点C恰与点A重合,将沿着翻折,点C恰与点A重合.结论①;②;③;④,正确的有( ).
A.1个 B.2个 C.3个 D.4个
6.如图,将长方形ABCD沿线段EF折叠到的位置,若,则的度数为( )
A. B. C. D.
7.如图,直线与两坐标轴分别交于两点,,D、E分别是直线轴上的动点,则周长的最小值是( ).
A. B. C. D.
8.将长为2、宽为a(a大于1且小于2)的长方形纸片按如图①所示的方式折叠并压平,剪下一个边长等于长方形宽的正方形,称为第一次操作;再把剩下的长方形按如图②所示的方式折叠并压平,剪下个边长等于此时长方形宽的正方形,称为第二次操作;如此反复操作下去…,若在第n次操作后,剩下的长方形恰为正方形,则操作终止.当n=3时,a的值为( )
A.1.8或1.5 B.1.5或1.2 C.1.5 D.1.2
二、填空题
9.点P(m,﹣2)与点P1(﹣4,n)关于x轴对称,则m,n的值分别为__
10.在平面直角坐标系中,点与点关于轴对称,则______.
11.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A坐标是,则经过第2020次变换后所得的A点坐标是________.
12.若点与关于某坐标轴对称,则 _________.
13.已知点,规定一次变换是:先作点关于轴对称,再将对称点向左平移1个单位长度,则连续经过2020次变换后,点的坐标变为______.
14.已知平面直角坐标系中,两点和,点在轴上,且使最短,则点的坐标是______.
三、解答题
15.如图,在平面直角坐标系中,已知△ABC.
(1)将△ABC向下平移6个单位,得△A1B1C1,画出△A1B1C1;
(2)画出△ABC关于y轴的对称图形△A2B2C2;
(3)并直接写出△ABC的面积.
16.如图,在平面直角坐标系中,.
(1)在图中作出关于轴对称的;
(2)的面积为______.
17.如图,的三个顶点坐标为,,.
(1)将向右平移3个单位,得到,画出图形;
(2)作出关于轴对称的图形,并直接写出点的坐标.
18.如图,在直角坐标系中,,,.
(1)在图中作出关于y轴对称的图形;并写出点的坐标.
(2)求的面积;
(3)在y轴上找一点P,使最小(请保留作图痕迹).
19.在平面直角坐标系中的位置如图所示.,,三点在格点上.
(1)作出关于轴对称的,并写出点的坐标______;
(2)在轴上找点,使得最小,作出点并写出点的坐标______(不用圆规,直尺就行);
(3)求的面积.
20.作图题(不写作法,保留作图痕迹,画出路径即可)
(1)请你设计一条路径,使得球P撞击台球桌边反射后,撞到球Q;
(2)请你设计一条路径,使得球P依次撞击台球桌边反射后,撞到球Q.
答案
一、单选题
B.D.B.A.B.A.A.B.
二、填空题
9.m=﹣4,n=2.
10.1.
11.(a,b).
12.3.
13.( 2017,3).
14.(1,0).
三、解答题
15.
解:(1)如图所示,△A1B1C1即为所求;
(2)如图所示,△A2B2C2即为所求;
(3)△ABC的面积为:3×4﹣×2×3﹣×2×2﹣×1×4=12﹣3﹣2﹣2=5.
16.
(1)如图所示:即为所求;
(2).
17.
解:如图所示,即为所求;
如图所示,即为所求,点的坐标为.
18.
(1)如图,为所作;点C1的坐标为(4,3);
(2)△ABC的面积=3×5 ×3×1 ×3×2 ×5×2=;
(3)如图,P点为所求.
.
19.
(1)作图如下,写出坐标
故答案为:;
(2)作图如下,写出坐标
故答案为:;
(3).
20.
解:(1)如图,运动路径:P→M→Q,点M即为所求.
(2)如图,运动路径:P→E→F→Q,点E,点F即为所求.
