八年级数学上册试题 11.1平面内的点坐标同步练习-沪科版(含答案)
文档属性
| 名称 | 八年级数学上册试题 11.1平面内的点坐标同步练习-沪科版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 686.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-05 00:00:00 | ||
图片预览


文档简介
11.1平面内的点坐标
第一课时
一、单选题
1.如果点在第二象限,那么的取值范围是( )
A. B. C. D.
2.点在轴的下方,轴的左侧,到轴的距离是,到轴的距离是,则点的坐标是( )
A. B. C. D.
3.若点在第三象限,则点一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.如图,平面直角坐标系中,一蚂蚁从点出发,沿着循环爬行,其中点的坐标为,点的坐标为,点的坐标为,点的坐标为,当蚂蚁爬了个单位时,蚂蚁所处位置的坐标为( )
A. B. C. D.
5.在平面直角坐标系中,点A(0,a),点B(0,4﹣a),且A在B的下方,点C(1,2),连接AC,BC,若在AB,BC,AC所围成区域内(含边界),横坐标和纵坐标都为整数的点的个数为4个,那么a的取值范围为( )
A.﹣1a0 B.0a1 C.1a2 D.﹣1a1
二、填空题
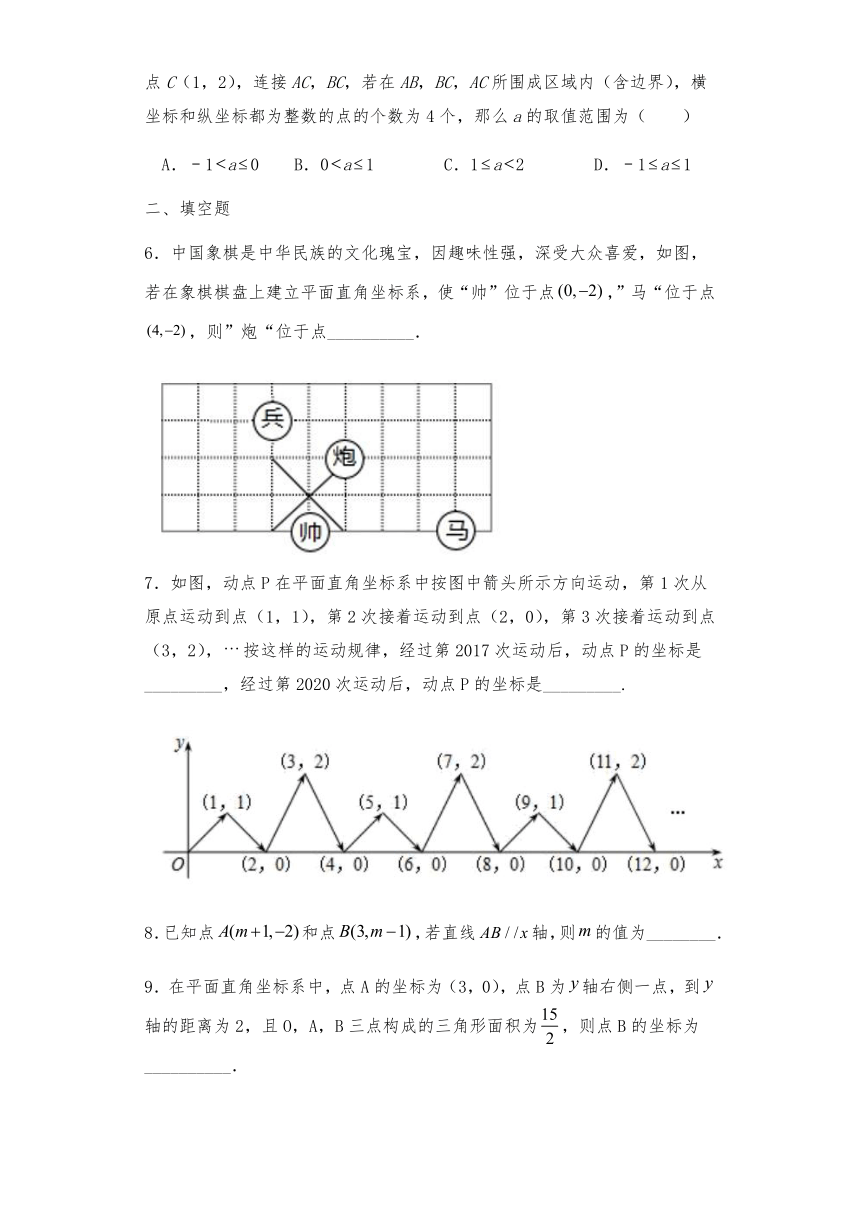
6.中国象棋是中华民族的文化瑰宝,因趣味性强,深受大众喜爱,如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点,”马“位于点,则”炮“位于点__________.
7.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),按这样的运动规律,经过第2017次运动后,动点P的坐标是_________,经过第2020次运动后,动点P的坐标是_________.
8.已知点和点,若直线轴,则的值为________.
9.在平面直角坐标系中,点A的坐标为(3,0),点B为轴右侧一点,到轴的距离为2,且O,A,B三点构成的三角形面积为,则点B的坐标为__________.
三、解答题
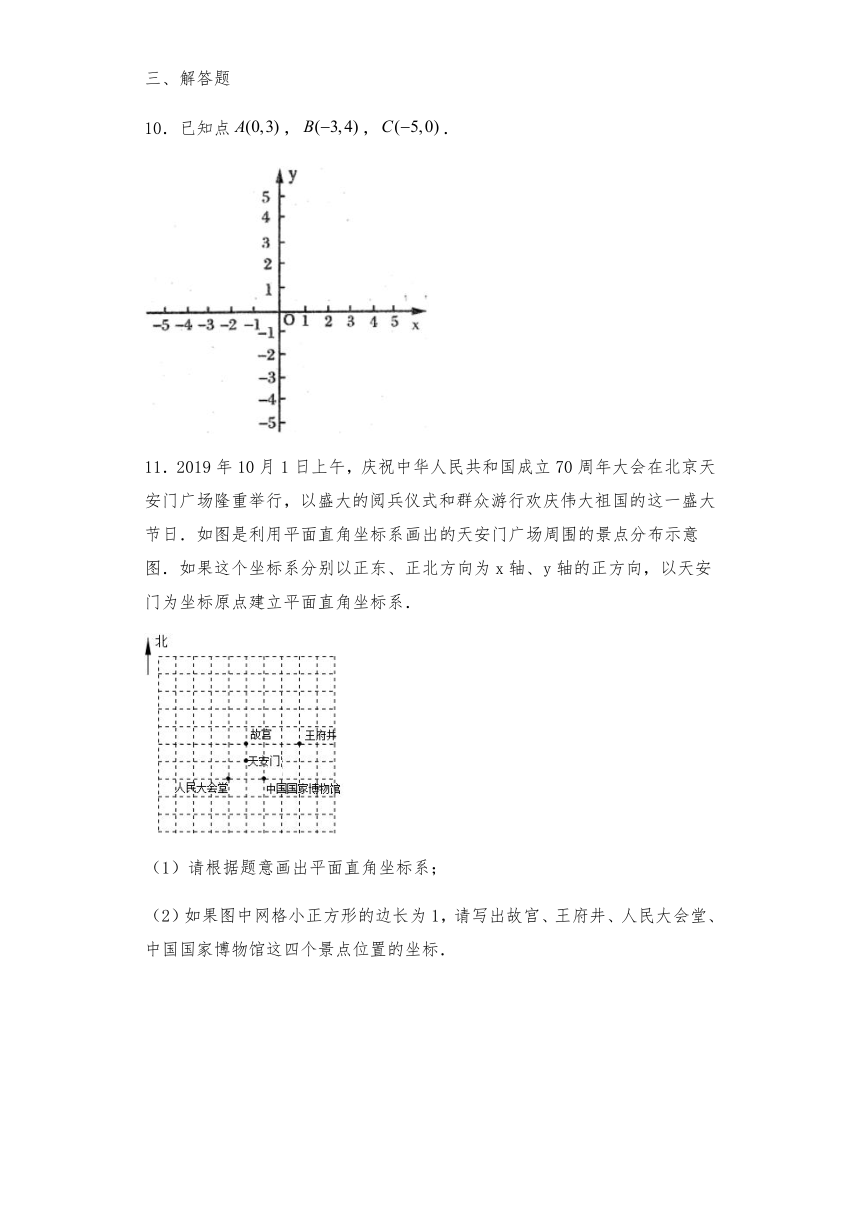
10.已知点,,.
11.2019年10月1日上午,庆祝中华人民共和国成立70周年大会在北京天安门广场隆重举行,以盛大的阅兵仪式和群众游行欢庆伟大祖国的这一盛大节日.如图是利用平面直角坐标系画出的天安门广场周围的景点分布示意图.如果这个坐标系分别以正东、正北方向为x轴、y轴的正方向,以天安门为坐标原点建立平面直角坐标系.
(1)请根据题意画出平面直角坐标系;
(2)如果图中网格小正方形的边长为1,请写出故宫、王府井、人民大会堂、中国国家博物馆这四个景点位置的坐标.
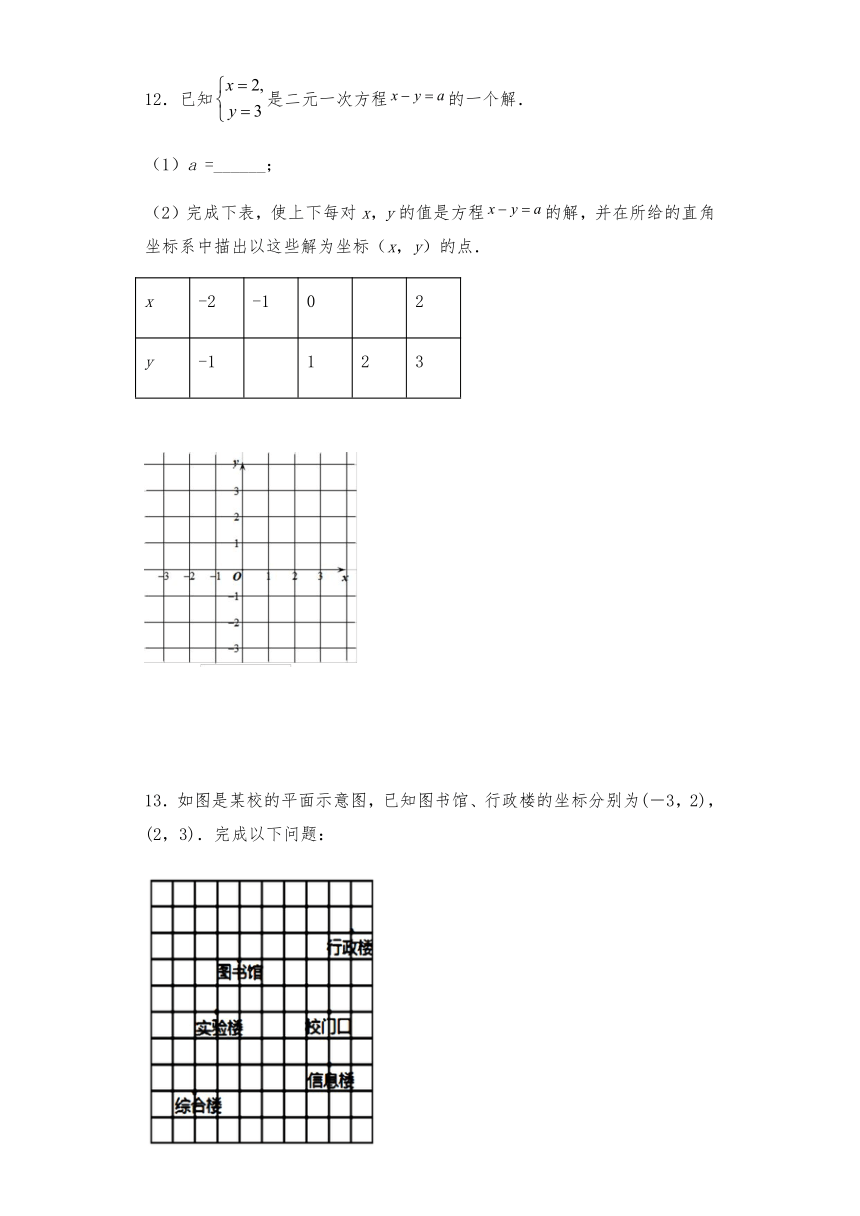
12.已知是二元一次方程的一个解.
(1)a =______;
(2)完成下表,使上下每对x,y的值是方程的解,并在所给的直角坐标系中描出以这些解为坐标(x,y)的点.
x -2 -1 0 2
y -1 1 2 3
13.如图是某校的平面示意图,已知图书馆、行政楼的坐标分别为(-3,2),(2,3).完成以下问题:
(1)请根据题意在图上建立直角坐标系;
(2)写出图上其他四个地点实验楼、校门口、综合楼、信息楼的坐标;
(3)在图中用点P表示体育馆(-1,-3)的位置.
14.在平面直角坐标系中,我们把到两坐标轴距离相等的点叫做“等轴距点”.
如图1,P,Q为两个“等轴距点”.作PE∥x轴,QE∥y轴,E为交点;作PF∥y轴,QF∥x轴,F为交点.我们把由此得到的长方形PEQF叫做P,Q两点的“轴距长方形”.
请根据上述定义,解答下面的题目:
如图2,在平面直角坐标系中,A(2,2),B(﹣1,1)都是“等轴距点”,长方形ACBD为A,B两点的“轴距长方形”.
(1)A,B两点的“轴距长方形”ACBD的周长为 ;
(2)点M为“等轴距点”,B,M两点的“轴距长方形”为周长等于8的正方形,求M点的坐标;
(3)在平面直角坐标系中,是否存在“等轴距点”N,使得A,N两点的“轴距长方形”的周长为12?若存在,请直接写出点N的坐标;若不存在,请说明理由.
第二课时
一、单选题
1.以二元一次方程组的解为坐标的点(x,y)在平面直角坐标系的( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1) →(1,1) →(1,0)→…],且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是( )
A.(4,O) B.(5,0) C.(0,5) D.(5,5)
3.点的横坐标是,且到轴的距离为,则点的坐标是( )
A.或 B.或 C. D.
4.如图所示,一个动点在第一象限内及x轴、y轴上运动,在第一秒内它由原点移动到(0,1)点,而后接着按图所示在x轴,y轴平行的方向运动,且每秒移动一个单位长度,那么动点运动到点(7,7)的位置时,所用的时间为( )秒.
A.30 B.42 C.56 D.72
5.如图,直角坐标平面xOy内,动点P按图中箭头所示方向依次运动,第1次从点(–1,0)运动到点(0,1),第2次运动到点(1,0),第3次运动到点(2,–2),……,按这样的运动规律,动点P第2018次运动到点
A.(,0) B.(,0) C.(,1) D.(,–2)
二、填空题
6.若点A(﹣2,n)在x轴上,则点B(n﹣1,n+1)在第_____象限.
7.已知点A在x轴的下方,且到x轴的距离为5,到y轴的距离为3,则点A的坐标为_____.
8.已知AB//y轴,A点的坐标为(3,2),并且AB=5,则B的坐标为__________.
9.已知点P(x,y)位于第二象限,并且y≤2x+6,x、y为整数,则点P的个数是____.
三、解答题
10.如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动,它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.例如从A到B记为:A→B(+1,+4),从D到C记为:D→C(﹣1,+2),其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中A→C(______,_____),B→C(______,_____),D→_____(﹣4,﹣2);
(2)若这只甲虫从A处去P处的行走路线依次为(+2,+2),(+2,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出P的位置;
(3)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程.
11.已知平面直角坐标系中,点P的坐标为
(1)当m为何值时,点P到x轴的距离为1
(2)当m为何值时,点P到y轴的距离为2?
(3)点P可能在第一象限坐标轴夹角的平分线上吗?若可能,求出m的值;若不可能,请说明理由.
12.如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+2|+(b﹣4)2=0.
(1)填空:a=_____,b=_____;
(2)如果在第三象限内有一点M(﹣3,m),请用含m的式子表示△ABM的面积;
(3)在(2)条件下,当m=﹣3时,在y轴上有一点P,使得△ABP的面积与△ABM的面积相等,请求出点P的坐标.
13.如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=4.
(1)求点B的坐标,并画出△ABC;
(2)求△ABC的面积;
(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由
14.如图,在平面直角坐标系中,已知点A(0,4),B(8,0),C(8,6)三点.
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(m,1),且四边形ABOP的面积是△ABC的面积的两倍;求满足条件的P点的坐标.
第一课时答案
一、单选题
A.A.B.A.B.
二、填空题
6.(1,0).
7.
8.-1.
9.(2,5)或(2, 5)
三、解答题
10.
(1)如图所示:
(2)解:过作轴于,则,,
∴
.
11.
解:(1)以天安门为坐标原点建立平面直角坐标系如图所示:
(2)各景点的坐标分别是:故宫(0,1)、王府井(3,1)、人民大会堂(﹣1,﹣1)、中国国家博物馆(1,﹣1).
12.(1) 把代入方程得:2-3=a
∴a=-1
(2)当x=﹣2时,﹣2-y=﹣1,解得:y=﹣1,
当x=﹣1时,﹣1-y=﹣1,解得:y=0,
当x=0时,0-y=﹣1,解得y=1;
当x=1时,1-y=﹣1,解得:y=2,
将x=2时,2-y=﹣1,解得:y=3.
完成表格:
x -2 -1 0 1 2
y -1 0 1 2 3
各点在坐标系中的位置如图所示:
13.
(1)由图书馆、行政楼的坐标分别为(-3,2),(2,3)可找到O(0,0)点,从而建立平面直角坐标系,如下图;
(2)根据(1)中的平面直角坐标系,可得其他四个地点的坐标.
故实验楼(-4,0);校门口(1,0);综合楼(-5,-3);信息楼(1,-2);
(3)根据平面直角坐标系,P(-1,-3)的位置如下图,
14.(1)∵A(2,2),B(﹣1,1),长方形ACBD为A,B两点的“轴距长方形”,
∴AD=BC=3,AC=BD=1,
∴“轴距长方形”ACBD的周长=2×(1+3)=8,
故答案为:8;
(2)∵B,M两点的“轴距长方形”为周长等于8的正方形,
∴正方形的边长为2,
∴点M的横坐标为﹣1+2=1或﹣1﹣2=﹣3,点M的纵坐标为1+2=3或1﹣2=﹣1,
∵点M为“等轴距点”,
∴点M(﹣3,3)或(1,﹣1);
(3)当点N的坐标为(a,a)时,
∵A,N两点的“轴距长方形”的周长为12,
∴2(|a﹣2|+|a﹣2|)=12
∴a=﹣1或a=5,
∴点N的坐标为(﹣1,﹣1)或(5,5);
当点N的坐标为(a,﹣a)时,
∵A,N两点的“轴距长方形”的周长为12,
∴2(|a﹣2|+|a+2|)=12
∴a=﹣3或a=3,
∴点N的坐标为(﹣3,﹣3)或(3,3);
综上所述:点N的坐标为(﹣1,﹣1)或(5,5)或(﹣3,﹣3)或(3,3).
第二课时答案
一、单选题
A.B.B.C.B.
二、填空题
6.二.
7.(3,﹣5)或(﹣3,﹣5).
8.(3,7)或(3,-3).
9.6.
三、解答题
10.
(1)规定:向上向右走为正,向下向左走为负∴A→C记为(3,4)B→C记为(2,0)D→A记为(﹣4,﹣2);
(2)P点位置如图所示.
(3)据已知条件可知:A→B表示为:(1,4),B→C记为(2,0)C→D记为(1,﹣2);
该甲虫走过的路线长为1+4+2+1+2=10.
故答案为(3,4);(2,0);A;
11.
解:点P到x轴的距离为1,,
点P到y轴的距离为2,,
如果点P可能在第一象限坐标轴夹角的平分线上点P在第一象限
,,不合题意
点P不可能在第一象限坐标轴夹角的平分线上.
12.(1)由题意得:a+2=0,b﹣4=4,
∴a=﹣2,b=4;
(2)作MC⊥x轴交x轴于点C,
∵A(﹣2,0),B(4,0),
∴AB=6,
∵MC=﹣m,
∴S△ABM=AB·MC=×6×(﹣m)=﹣3m;
(3)m=﹣3时,S△ABM=﹣3×(﹣3)=9,
设P(0,a),
OP= |a|,
∴S△ABP=AB·OP=×6×|a|=3 |a|,
∴3 |a|=9,
解得a=±3,
∴P(0,3)或(0,﹣3).
13.
(1)由于A(﹣1,0),点B在x轴上,且AB=4.
若B在A左边,则B的横坐标为-1-4=-5;
若B在A右边,则B的横坐标为-1+4=3;
故B(-5,0),(3,0);
(2)点C到x轴的距离为4.则S= ;
(3)设点P到x轴的距离为h,则×4h=10,
解得h=5,
点P在y轴正半轴时,P(0,5),
点P在y轴负半轴时,P(0, 5),
综上所述,点P的坐标为(0,5)或(0, 5).
14.(1)∵B(8,0),C(8,6),
∴BC=6,
∴S△ABC= ×6×8=24;
(2)∵A(0,4)(8,0),
∴OA=4,OB=8,
∴S四边形ABOP=S△AOB+S△AOP
= ×4×8+ ×4(﹣m)=16﹣2m,
又∵S四边形ABOP=2S△ABC=48,
∴16﹣2m=48,
解得:m=﹣16,
∴P(﹣16,1).
第一课时
一、单选题
1.如果点在第二象限,那么的取值范围是( )
A. B. C. D.
2.点在轴的下方,轴的左侧,到轴的距离是,到轴的距离是,则点的坐标是( )
A. B. C. D.
3.若点在第三象限,则点一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.如图,平面直角坐标系中,一蚂蚁从点出发,沿着循环爬行,其中点的坐标为,点的坐标为,点的坐标为,点的坐标为,当蚂蚁爬了个单位时,蚂蚁所处位置的坐标为( )
A. B. C. D.
5.在平面直角坐标系中,点A(0,a),点B(0,4﹣a),且A在B的下方,点C(1,2),连接AC,BC,若在AB,BC,AC所围成区域内(含边界),横坐标和纵坐标都为整数的点的个数为4个,那么a的取值范围为( )
A.﹣1a0 B.0a1 C.1a2 D.﹣1a1
二、填空题
6.中国象棋是中华民族的文化瑰宝,因趣味性强,深受大众喜爱,如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点,”马“位于点,则”炮“位于点__________.
7.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),按这样的运动规律,经过第2017次运动后,动点P的坐标是_________,经过第2020次运动后,动点P的坐标是_________.
8.已知点和点,若直线轴,则的值为________.
9.在平面直角坐标系中,点A的坐标为(3,0),点B为轴右侧一点,到轴的距离为2,且O,A,B三点构成的三角形面积为,则点B的坐标为__________.
三、解答题
10.已知点,,.
11.2019年10月1日上午,庆祝中华人民共和国成立70周年大会在北京天安门广场隆重举行,以盛大的阅兵仪式和群众游行欢庆伟大祖国的这一盛大节日.如图是利用平面直角坐标系画出的天安门广场周围的景点分布示意图.如果这个坐标系分别以正东、正北方向为x轴、y轴的正方向,以天安门为坐标原点建立平面直角坐标系.
(1)请根据题意画出平面直角坐标系;
(2)如果图中网格小正方形的边长为1,请写出故宫、王府井、人民大会堂、中国国家博物馆这四个景点位置的坐标.
12.已知是二元一次方程的一个解.
(1)a =______;
(2)完成下表,使上下每对x,y的值是方程的解,并在所给的直角坐标系中描出以这些解为坐标(x,y)的点.
x -2 -1 0 2
y -1 1 2 3
13.如图是某校的平面示意图,已知图书馆、行政楼的坐标分别为(-3,2),(2,3).完成以下问题:
(1)请根据题意在图上建立直角坐标系;
(2)写出图上其他四个地点实验楼、校门口、综合楼、信息楼的坐标;
(3)在图中用点P表示体育馆(-1,-3)的位置.
14.在平面直角坐标系中,我们把到两坐标轴距离相等的点叫做“等轴距点”.
如图1,P,Q为两个“等轴距点”.作PE∥x轴,QE∥y轴,E为交点;作PF∥y轴,QF∥x轴,F为交点.我们把由此得到的长方形PEQF叫做P,Q两点的“轴距长方形”.
请根据上述定义,解答下面的题目:
如图2,在平面直角坐标系中,A(2,2),B(﹣1,1)都是“等轴距点”,长方形ACBD为A,B两点的“轴距长方形”.
(1)A,B两点的“轴距长方形”ACBD的周长为 ;
(2)点M为“等轴距点”,B,M两点的“轴距长方形”为周长等于8的正方形,求M点的坐标;
(3)在平面直角坐标系中,是否存在“等轴距点”N,使得A,N两点的“轴距长方形”的周长为12?若存在,请直接写出点N的坐标;若不存在,请说明理由.
第二课时
一、单选题
1.以二元一次方程组的解为坐标的点(x,y)在平面直角坐标系的( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1) →(1,1) →(1,0)→…],且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是( )
A.(4,O) B.(5,0) C.(0,5) D.(5,5)
3.点的横坐标是,且到轴的距离为,则点的坐标是( )
A.或 B.或 C. D.
4.如图所示,一个动点在第一象限内及x轴、y轴上运动,在第一秒内它由原点移动到(0,1)点,而后接着按图所示在x轴,y轴平行的方向运动,且每秒移动一个单位长度,那么动点运动到点(7,7)的位置时,所用的时间为( )秒.
A.30 B.42 C.56 D.72
5.如图,直角坐标平面xOy内,动点P按图中箭头所示方向依次运动,第1次从点(–1,0)运动到点(0,1),第2次运动到点(1,0),第3次运动到点(2,–2),……,按这样的运动规律,动点P第2018次运动到点
A.(,0) B.(,0) C.(,1) D.(,–2)
二、填空题
6.若点A(﹣2,n)在x轴上,则点B(n﹣1,n+1)在第_____象限.
7.已知点A在x轴的下方,且到x轴的距离为5,到y轴的距离为3,则点A的坐标为_____.
8.已知AB//y轴,A点的坐标为(3,2),并且AB=5,则B的坐标为__________.
9.已知点P(x,y)位于第二象限,并且y≤2x+6,x、y为整数,则点P的个数是____.
三、解答题
10.如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动,它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.例如从A到B记为:A→B(+1,+4),从D到C记为:D→C(﹣1,+2),其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中A→C(______,_____),B→C(______,_____),D→_____(﹣4,﹣2);
(2)若这只甲虫从A处去P处的行走路线依次为(+2,+2),(+2,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出P的位置;
(3)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程.
11.已知平面直角坐标系中,点P的坐标为
(1)当m为何值时,点P到x轴的距离为1
(2)当m为何值时,点P到y轴的距离为2?
(3)点P可能在第一象限坐标轴夹角的平分线上吗?若可能,求出m的值;若不可能,请说明理由.
12.如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+2|+(b﹣4)2=0.
(1)填空:a=_____,b=_____;
(2)如果在第三象限内有一点M(﹣3,m),请用含m的式子表示△ABM的面积;
(3)在(2)条件下,当m=﹣3时,在y轴上有一点P,使得△ABP的面积与△ABM的面积相等,请求出点P的坐标.
13.如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=4.
(1)求点B的坐标,并画出△ABC;
(2)求△ABC的面积;
(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由
14.如图,在平面直角坐标系中,已知点A(0,4),B(8,0),C(8,6)三点.
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(m,1),且四边形ABOP的面积是△ABC的面积的两倍;求满足条件的P点的坐标.
第一课时答案
一、单选题
A.A.B.A.B.
二、填空题
6.(1,0).
7.
8.-1.
9.(2,5)或(2, 5)
三、解答题
10.
(1)如图所示:
(2)解:过作轴于,则,,
∴
.
11.
解:(1)以天安门为坐标原点建立平面直角坐标系如图所示:
(2)各景点的坐标分别是:故宫(0,1)、王府井(3,1)、人民大会堂(﹣1,﹣1)、中国国家博物馆(1,﹣1).
12.(1) 把代入方程得:2-3=a
∴a=-1
(2)当x=﹣2时,﹣2-y=﹣1,解得:y=﹣1,
当x=﹣1时,﹣1-y=﹣1,解得:y=0,
当x=0时,0-y=﹣1,解得y=1;
当x=1时,1-y=﹣1,解得:y=2,
将x=2时,2-y=﹣1,解得:y=3.
完成表格:
x -2 -1 0 1 2
y -1 0 1 2 3
各点在坐标系中的位置如图所示:
13.
(1)由图书馆、行政楼的坐标分别为(-3,2),(2,3)可找到O(0,0)点,从而建立平面直角坐标系,如下图;
(2)根据(1)中的平面直角坐标系,可得其他四个地点的坐标.
故实验楼(-4,0);校门口(1,0);综合楼(-5,-3);信息楼(1,-2);
(3)根据平面直角坐标系,P(-1,-3)的位置如下图,
14.(1)∵A(2,2),B(﹣1,1),长方形ACBD为A,B两点的“轴距长方形”,
∴AD=BC=3,AC=BD=1,
∴“轴距长方形”ACBD的周长=2×(1+3)=8,
故答案为:8;
(2)∵B,M两点的“轴距长方形”为周长等于8的正方形,
∴正方形的边长为2,
∴点M的横坐标为﹣1+2=1或﹣1﹣2=﹣3,点M的纵坐标为1+2=3或1﹣2=﹣1,
∵点M为“等轴距点”,
∴点M(﹣3,3)或(1,﹣1);
(3)当点N的坐标为(a,a)时,
∵A,N两点的“轴距长方形”的周长为12,
∴2(|a﹣2|+|a﹣2|)=12
∴a=﹣1或a=5,
∴点N的坐标为(﹣1,﹣1)或(5,5);
当点N的坐标为(a,﹣a)时,
∵A,N两点的“轴距长方形”的周长为12,
∴2(|a﹣2|+|a+2|)=12
∴a=﹣3或a=3,
∴点N的坐标为(﹣3,﹣3)或(3,3);
综上所述:点N的坐标为(﹣1,﹣1)或(5,5)或(﹣3,﹣3)或(3,3).
第二课时答案
一、单选题
A.B.B.C.B.
二、填空题
6.二.
7.(3,﹣5)或(﹣3,﹣5).
8.(3,7)或(3,-3).
9.6.
三、解答题
10.
(1)规定:向上向右走为正,向下向左走为负∴A→C记为(3,4)B→C记为(2,0)D→A记为(﹣4,﹣2);
(2)P点位置如图所示.
(3)据已知条件可知:A→B表示为:(1,4),B→C记为(2,0)C→D记为(1,﹣2);
该甲虫走过的路线长为1+4+2+1+2=10.
故答案为(3,4);(2,0);A;
11.
解:点P到x轴的距离为1,,
点P到y轴的距离为2,,
如果点P可能在第一象限坐标轴夹角的平分线上点P在第一象限
,,不合题意
点P不可能在第一象限坐标轴夹角的平分线上.
12.(1)由题意得:a+2=0,b﹣4=4,
∴a=﹣2,b=4;
(2)作MC⊥x轴交x轴于点C,
∵A(﹣2,0),B(4,0),
∴AB=6,
∵MC=﹣m,
∴S△ABM=AB·MC=×6×(﹣m)=﹣3m;
(3)m=﹣3时,S△ABM=﹣3×(﹣3)=9,
设P(0,a),
OP= |a|,
∴S△ABP=AB·OP=×6×|a|=3 |a|,
∴3 |a|=9,
解得a=±3,
∴P(0,3)或(0,﹣3).
13.
(1)由于A(﹣1,0),点B在x轴上,且AB=4.
若B在A左边,则B的横坐标为-1-4=-5;
若B在A右边,则B的横坐标为-1+4=3;
故B(-5,0),(3,0);
(2)点C到x轴的距离为4.则S= ;
(3)设点P到x轴的距离为h,则×4h=10,
解得h=5,
点P在y轴正半轴时,P(0,5),
点P在y轴负半轴时,P(0, 5),
综上所述,点P的坐标为(0,5)或(0, 5).
14.(1)∵B(8,0),C(8,6),
∴BC=6,
∴S△ABC= ×6×8=24;
(2)∵A(0,4)(8,0),
∴OA=4,OB=8,
∴S四边形ABOP=S△AOB+S△AOP
= ×4×8+ ×4(﹣m)=16﹣2m,
又∵S四边形ABOP=2S△ABC=48,
∴16﹣2m=48,
解得:m=﹣16,
∴P(﹣16,1).
