八年级数学上册试题 11.2图形在坐标系中的平移同步练习-沪科版(含答案)
文档属性
| 名称 | 八年级数学上册试题 11.2图形在坐标系中的平移同步练习-沪科版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 625.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-05 19:35:05 | ||
图片预览




文档简介
11.2图形在坐标系中的平移
第一课时
一、单选题
1.在平面直角坐标系xOy中,线段AB的两个端点坐标分别为A(-1,-1),B(1,2),平移线段AB得到线段A’B’(点A与A’对应),已知A’的坐标为(3,-1),则点B’的坐标为( )
A.(4,2) B.(5,2) C.(6,2) D.(5,3)
2.在平面直角坐标系中,将点向右平移个单位长度后得到的点的坐标为( )
A. B. C. D.
3.如图,A,B的坐标为,,若将线段AB平移至,则的值为
A.1 B. C.0 D.2
4.右图是老北京城一些地点的分布示意图.在图中,分别以正东、正北方向为轴、轴的正方向建立平面直角坐标系,有如下四个结论:
①当表示天安门的点的坐标为(0,0),表示广安门的点的坐标为(,)时,表示左安门的点的坐标为(5,);
②当表示天安门的点的坐标为(0,0),表示广安门的点的坐标为(,)时,表示左安门的点的坐标为(10,);
③当表示天安门的点的坐标为(1,1),表示广安门的点的坐标为(,)时,表示左安门的点的坐标为(,);
④当表示天安门的点的坐标为(,),表示广安门的点的坐标为(,)时,表示左安门的点的坐标为(,).
上述结论中,所有正确结论的序号是
A.①③ B.②③④ C.①④ D.①②③④
5.已知点A的坐标为(1,3),点B的坐标为(2,1).将线段AB沿某一方向平移后,点A的对应点的坐标为(﹣2,1).则点B的对应点的坐标为( )
A.(5,3) B.(﹣1,﹣2) C.(﹣1,﹣1) D.(0,﹣1)
二、填空题
6.将点P(﹣3,y)向下平移3个单位,向左平移2个单位后得到点Q(x,﹣1),则x+y=_____.
7.已知线段MN平行于x轴,且MN的长度为5,若,则点N的坐标______.
8.通过平移把点A(2,-1)移到点A′(2,2),按同样的平移方式,点B(-3,1)移动到点B′,则点B′的坐标是________.
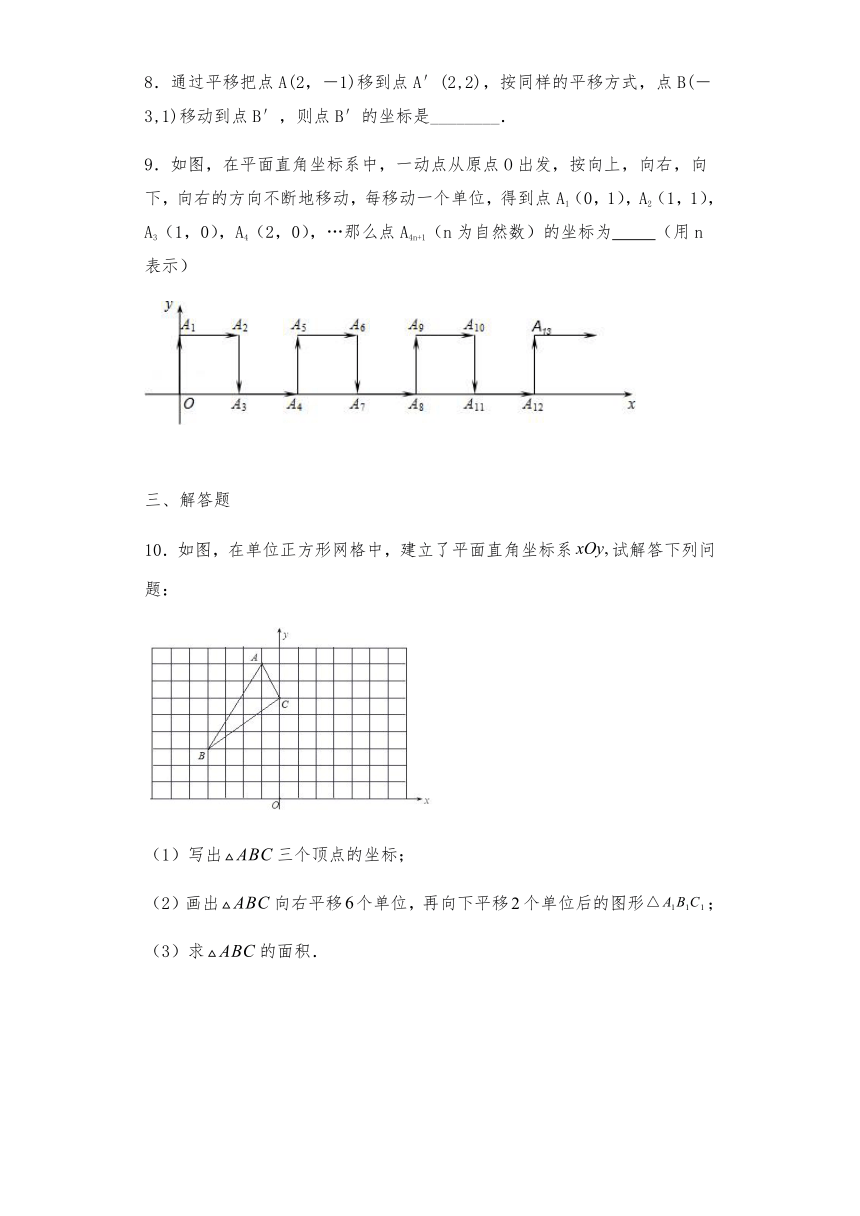
9.如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A4n+1(n为自然数)的坐标为 (用n表示)
三、解答题
10.如图,在单位正方形网格中,建立了平面直角坐标系试解答下列问题:
(1)写出三个顶点的坐标;
(2)画出向右平移个单位,再向下平移个单位后的图形;
(3)求的面积.
11.如图所示,三角形记作在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,先将向上平移3个单位长度,再向右平移2个单位长度,得到.
三个顶点的坐标分别是:______,______,______,
在图中画出;
平移后的三个顶点坐标分别为:______、______、______;
若y轴有一点P,使与面积相等,则P点的坐标为______.
12.如图,平面直角坐标系中,已知点A(﹣3,3),B(﹣5,1),C(﹣2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b﹣2 ).
(1)直接写出点A1,B1,C1的坐标.
(2)在图中画出△A1B1C1.
(3)连接A A1,求△AOA1的面积.
13.阅读下面的文字,解答问题.
如图,在平面直角坐标系中,点D的坐标是(﹣3,1),点A的坐标是(4,3).
(1)点B和点C的坐标分别是________、________.
(2)将△ABC平移后使点C与点D重合,点A、B分别与点E、F重合,画出△DEF.并直接写出E点的坐标 ,F点的坐标 .
(3)若AB上的点M坐标为(x,y),则平移后的对应点M′的坐标为___ _____.
(4)求的面积.
14.△ABC与△A'B'C'在平面直角坐标系中的位置如图所示
(1)分别写出下列各点的坐标:A_______ B_______ C_______
(2)△ABC由△A'B'C'经过怎样的平移得到
(3)若点P(x,y)是△ABC内部点,则A'B'C' 内部的对应点P'的坐标为
(4)求△ABC的面积
第二课时
一、单选题
1.线段AB两端点坐标分别为A(–1,4),B(–4,1),现将它向左平移4个单位长度,得到线段A1B1,则A1、B1的坐标分别为( )
A.A1(–5,0),B1(–8,–3) B.A1(3,7),B1(0,5)
C.A1(–5,4),B1(-8,1) D.A1(3,4),B1(0,1)
2.将点向左平移个单位长度,在向上平移个单位长度得到点,则点的坐标是( )
A. B. C. D.
3.若将点A先向左平移1个单位,再向上平移4个单位,得到的B(-3,2),则点A的坐标为( )
A.(-1,6) B.(-4,6) C.(-2,-2) D.(-4,-2)
4.已知△ABC顶点坐标分别是A(0,6),B(﹣3,﹣3),C(1,0),将△ABC平移后顶点A的对应点A1的坐标是(4,10),则点B的对应点B1的坐标为( )
A.(7,1) B.B(1,7) C.(1,1) D.(2,1)
5.将点A(x,1-y)向下平移5个单位长度得到点B(1+y,x),则点(x,y)在平面直角坐标系的( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
二、填空题
6.如图,在平面直角坐标系中,一动点从原点O出发,按向上.向右.向下.向右的方向依次平移,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A2016的坐标为________.
7.已知点m(3a9,1a),将m点向左平移3个单位长度后落在y轴上,则a= __________ .
8.规定:在平面直角坐标系xOy中,“把某一图形先沿x轴翻折,再沿y轴翻折”为一次变化.如图,已知正方形ABCD,顶点A(1,3),C(3,1).若正方形ABCD经过一次上述变化,则点A变化后的坐标为 ,如此这样,对正方形ABCD连续做2015次这样的变化,则点D变化后的坐标为 .
9.已知长方形ABCD在平面直角坐标系中的位置如图所示,将长方形ABCD沿x轴向左平移到使点C与坐标原点重合后,再沿y轴向下平移到使点D与坐标原点重合,此时点A的坐标是______,点B的坐标是______,点C的坐标是______.
三、解答题
10.如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(﹣4,4),B(﹣2,5),C(﹣2,1).
(1)平移△ABC,使点C移到点C1(﹣2,﹣4),画出平移后的△A1B1C1,并写出点A1,B1的坐标;
(2)将△ABC绕点(0,3)旋转180°,得到△A2B2C2,画出旋转后的△A2B2C2;
11.如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题:
(1)平移后的三个顶点坐标分别为:A1 ,B1 ,C1 ;
(2)画出平移后三角形A1B1C1;
(3)求三角形ABC的面积.
12.在如图所示的平面直角坐标系中表示下面各点A(0,3),B(1,-3),C(3,-5),D(-3,-5),E(3,5),F(5,6),G(5,0)根据描点回答问题:
(1)A点到原点的距离是________.
(2)将点C向x轴的负方向平移6个单位,它与点______重合.
(3)连接CE,则直线CE与坐标轴是什么关系?
(4)在以上七个点中,任意两点所形成的直线中,直接写出互相垂直的直线.
13.如图所示,△A′B′C′是△ABC经过平移得到的,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).
(1)请写出三角形ABC平移的过程;
(2)分别写出点A′,B′,C′ 的坐标.
(3)求△A′B′C′的面积.
14.类比学习:一动点沿着数轴先向右平移3个单位长度,再向左平移2个单位长度,相当于向右平移1个单位长度.用实数加法表示为3+(-2)=1.若坐标平面上的点有如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移|a|个单位长度),沿y轴方向平移的数量为b(向上为正,向下为负,平移|b|个单位长度),则把有序数对{a,b}叫做这一平移的“平移量”,“平移量”{a,b}与“平移量”{c,d}的加法运算法则为{a,b}+{c,d}={a+c,b+d}.
解决问题:
(1)计算:{3,1}+{1,2},{1,2}+{3,1}.
(2)动点P从坐标原点O出发,先按照“平移量”{3,1}平移到点A,再按照“平移量”{1,2}平移到点B;若先把动点P按照“平移量”{1,2}平移到点C,再按照“平移量”{3,1}平移,最后的位置还是点B吗?在图①中画出四边形OABC.
(3)如图②所示,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O.请用“平移量”加法算式表示它的航行过程.
第一课时答案
一、单选题
B.A.C.D.C.
二、填空题
6.-3.
7.(7,-2)或(-3,-2).
8.(-3,4).
9.(2n,1).
三、解答题
10.
(1)根据平面直角坐标系可得,;
(2) 图形如图:
(3) .
11.
解:观察图象可知,,;
故答案为,,;
如图即为所求;
平移后的三个顶点坐标分别为:、、;
故答案为,,;
如图,过点A作交y轴于P,
,
,此时.
作点P关于直线BC的对称点,则点也满足条件,此时,
综上所述,满足条件的点P坐标为或.
故答案为或.
12.解:
(1)∵点P(a,b)的对应点为P1(a+6,b-2),
∴平移规律为向右6个单位,向下2个单位,
∴A(-3,3),B(-5,1),C(-2,0)的对应点的坐标为A1(3,1),B1(1,-1),C1(4,-2);
(2)△A1B1C1如图所示;
(3)△AOA1的面积=6×3-×3×3-×3×1-×6×2,
=18---6,
=18-12,
=6.
13.
解:(1)(3,1);(1,2)
(2)解:如图所示,△DEF即为所求. 点E坐标为(0,2),点F坐标为(﹣1,0).
(3)(x﹣4,y﹣1)
(4)将补成长方形,减去3个直角三角形的面积得:
=6-1.5-1-1
=2.5
14.
解:(1)A(1,3); B(2,0);C(3,1);
(2)先向右平移4个单位,再向上平移2个单位;
或:先向上平移2个单位,再向右平移4个单位;
(3)P′(x-4,y-2);
(4)△ABC的面积=2×3-×1×3-×1×1-×2×2
=6-1.5-0.5-2
=2.
第二课时答案
一、单选题
C.D.C.C.C.
二、填空题
6.(1008,0).
7.4.
8.(-1,-3);(-3,-3)
9.(-5,0) (-5,-3) (0,-3)
三、解答题
10.
∴A1(-4,-1),B1(-2,0);
(2)如图所示,则△A2B2C2为所求作的三角形,
11.
(1) 观察图形可知点A(-2,2),点B(-5,-3),点C(0,-1),
所以将三角形ABC向右平移5个单位长度,再向上平移3个单位长度后所得对应点的坐标为:A1(3,5),B1(0,0),C1(5,2);
(2)△A1B1C1如图所示;
(3)△ABC的面积=5×5-×5×2-×2×3-×3×5
=25-5-3-7.5
=25-15.5
=9.5.
12.
解:由题意得,如图所示:
(1)A点到原点的距离是3.
(2)将点C向x轴的负方向平移6个单位,它与点D重合.
(3)直线CE与y轴平行,与x轴垂直;
(4)直线CD与CE垂直,直线CD与FG垂直.
故答案为:(1)3;(2)D;(3)垂直;(4)直线CD与CE垂直,直线CD与FG垂直.
13.
(1) △ABC先向右平移6个单位,再向上平移4个单位得到△A′B′C′或△ABC先向上平移4个单位,再向右平移6个单位得到△A′B′C′
(2) A′(2,3) B′(1,0) C′(5,1);
(3)S△A′B′C′=4×3 ×3×1 ×3×2 ×1×4=12 1.5 3 2=5.5.
14.
解:(1){3,1}+{1,2}={4,3};
{1,2}+{3,1}={4,3}.
(2) 画图如下:
最后的位置仍是B.
(3)从O出发,先向右平移2个单位,再向上平移3个单位,可知平移量为{2,3},
同理得到P到Q的平移量为{3,2},从Q到O的平移量为{-5,-5},故有{2,3}+{3,2}+{-5,-5}={0,0}.
第一课时
一、单选题
1.在平面直角坐标系xOy中,线段AB的两个端点坐标分别为A(-1,-1),B(1,2),平移线段AB得到线段A’B’(点A与A’对应),已知A’的坐标为(3,-1),则点B’的坐标为( )
A.(4,2) B.(5,2) C.(6,2) D.(5,3)
2.在平面直角坐标系中,将点向右平移个单位长度后得到的点的坐标为( )
A. B. C. D.
3.如图,A,B的坐标为,,若将线段AB平移至,则的值为
A.1 B. C.0 D.2
4.右图是老北京城一些地点的分布示意图.在图中,分别以正东、正北方向为轴、轴的正方向建立平面直角坐标系,有如下四个结论:
①当表示天安门的点的坐标为(0,0),表示广安门的点的坐标为(,)时,表示左安门的点的坐标为(5,);
②当表示天安门的点的坐标为(0,0),表示广安门的点的坐标为(,)时,表示左安门的点的坐标为(10,);
③当表示天安门的点的坐标为(1,1),表示广安门的点的坐标为(,)时,表示左安门的点的坐标为(,);
④当表示天安门的点的坐标为(,),表示广安门的点的坐标为(,)时,表示左安门的点的坐标为(,).
上述结论中,所有正确结论的序号是
A.①③ B.②③④ C.①④ D.①②③④
5.已知点A的坐标为(1,3),点B的坐标为(2,1).将线段AB沿某一方向平移后,点A的对应点的坐标为(﹣2,1).则点B的对应点的坐标为( )
A.(5,3) B.(﹣1,﹣2) C.(﹣1,﹣1) D.(0,﹣1)
二、填空题
6.将点P(﹣3,y)向下平移3个单位,向左平移2个单位后得到点Q(x,﹣1),则x+y=_____.
7.已知线段MN平行于x轴,且MN的长度为5,若,则点N的坐标______.
8.通过平移把点A(2,-1)移到点A′(2,2),按同样的平移方式,点B(-3,1)移动到点B′,则点B′的坐标是________.
9.如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A4n+1(n为自然数)的坐标为 (用n表示)
三、解答题
10.如图,在单位正方形网格中,建立了平面直角坐标系试解答下列问题:
(1)写出三个顶点的坐标;
(2)画出向右平移个单位,再向下平移个单位后的图形;
(3)求的面积.
11.如图所示,三角形记作在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,先将向上平移3个单位长度,再向右平移2个单位长度,得到.
三个顶点的坐标分别是:______,______,______,
在图中画出;
平移后的三个顶点坐标分别为:______、______、______;
若y轴有一点P,使与面积相等,则P点的坐标为______.
12.如图,平面直角坐标系中,已知点A(﹣3,3),B(﹣5,1),C(﹣2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b﹣2 ).
(1)直接写出点A1,B1,C1的坐标.
(2)在图中画出△A1B1C1.
(3)连接A A1,求△AOA1的面积.
13.阅读下面的文字,解答问题.
如图,在平面直角坐标系中,点D的坐标是(﹣3,1),点A的坐标是(4,3).
(1)点B和点C的坐标分别是________、________.
(2)将△ABC平移后使点C与点D重合,点A、B分别与点E、F重合,画出△DEF.并直接写出E点的坐标 ,F点的坐标 .
(3)若AB上的点M坐标为(x,y),则平移后的对应点M′的坐标为___ _____.
(4)求的面积.
14.△ABC与△A'B'C'在平面直角坐标系中的位置如图所示
(1)分别写出下列各点的坐标:A_______ B_______ C_______
(2)△ABC由△A'B'C'经过怎样的平移得到
(3)若点P(x,y)是△ABC内部点,则A'B'C' 内部的对应点P'的坐标为
(4)求△ABC的面积
第二课时
一、单选题
1.线段AB两端点坐标分别为A(–1,4),B(–4,1),现将它向左平移4个单位长度,得到线段A1B1,则A1、B1的坐标分别为( )
A.A1(–5,0),B1(–8,–3) B.A1(3,7),B1(0,5)
C.A1(–5,4),B1(-8,1) D.A1(3,4),B1(0,1)
2.将点向左平移个单位长度,在向上平移个单位长度得到点,则点的坐标是( )
A. B. C. D.
3.若将点A先向左平移1个单位,再向上平移4个单位,得到的B(-3,2),则点A的坐标为( )
A.(-1,6) B.(-4,6) C.(-2,-2) D.(-4,-2)
4.已知△ABC顶点坐标分别是A(0,6),B(﹣3,﹣3),C(1,0),将△ABC平移后顶点A的对应点A1的坐标是(4,10),则点B的对应点B1的坐标为( )
A.(7,1) B.B(1,7) C.(1,1) D.(2,1)
5.将点A(x,1-y)向下平移5个单位长度得到点B(1+y,x),则点(x,y)在平面直角坐标系的( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
二、填空题
6.如图,在平面直角坐标系中,一动点从原点O出发,按向上.向右.向下.向右的方向依次平移,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A2016的坐标为________.
7.已知点m(3a9,1a),将m点向左平移3个单位长度后落在y轴上,则a= __________ .
8.规定:在平面直角坐标系xOy中,“把某一图形先沿x轴翻折,再沿y轴翻折”为一次变化.如图,已知正方形ABCD,顶点A(1,3),C(3,1).若正方形ABCD经过一次上述变化,则点A变化后的坐标为 ,如此这样,对正方形ABCD连续做2015次这样的变化,则点D变化后的坐标为 .
9.已知长方形ABCD在平面直角坐标系中的位置如图所示,将长方形ABCD沿x轴向左平移到使点C与坐标原点重合后,再沿y轴向下平移到使点D与坐标原点重合,此时点A的坐标是______,点B的坐标是______,点C的坐标是______.
三、解答题
10.如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(﹣4,4),B(﹣2,5),C(﹣2,1).
(1)平移△ABC,使点C移到点C1(﹣2,﹣4),画出平移后的△A1B1C1,并写出点A1,B1的坐标;
(2)将△ABC绕点(0,3)旋转180°,得到△A2B2C2,画出旋转后的△A2B2C2;
11.如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题:
(1)平移后的三个顶点坐标分别为:A1 ,B1 ,C1 ;
(2)画出平移后三角形A1B1C1;
(3)求三角形ABC的面积.
12.在如图所示的平面直角坐标系中表示下面各点A(0,3),B(1,-3),C(3,-5),D(-3,-5),E(3,5),F(5,6),G(5,0)根据描点回答问题:
(1)A点到原点的距离是________.
(2)将点C向x轴的负方向平移6个单位,它与点______重合.
(3)连接CE,则直线CE与坐标轴是什么关系?
(4)在以上七个点中,任意两点所形成的直线中,直接写出互相垂直的直线.
13.如图所示,△A′B′C′是△ABC经过平移得到的,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).
(1)请写出三角形ABC平移的过程;
(2)分别写出点A′,B′,C′ 的坐标.
(3)求△A′B′C′的面积.
14.类比学习:一动点沿着数轴先向右平移3个单位长度,再向左平移2个单位长度,相当于向右平移1个单位长度.用实数加法表示为3+(-2)=1.若坐标平面上的点有如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移|a|个单位长度),沿y轴方向平移的数量为b(向上为正,向下为负,平移|b|个单位长度),则把有序数对{a,b}叫做这一平移的“平移量”,“平移量”{a,b}与“平移量”{c,d}的加法运算法则为{a,b}+{c,d}={a+c,b+d}.
解决问题:
(1)计算:{3,1}+{1,2},{1,2}+{3,1}.
(2)动点P从坐标原点O出发,先按照“平移量”{3,1}平移到点A,再按照“平移量”{1,2}平移到点B;若先把动点P按照“平移量”{1,2}平移到点C,再按照“平移量”{3,1}平移,最后的位置还是点B吗?在图①中画出四边形OABC.
(3)如图②所示,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O.请用“平移量”加法算式表示它的航行过程.
第一课时答案
一、单选题
B.A.C.D.C.
二、填空题
6.-3.
7.(7,-2)或(-3,-2).
8.(-3,4).
9.(2n,1).
三、解答题
10.
(1)根据平面直角坐标系可得,;
(2) 图形如图:
(3) .
11.
解:观察图象可知,,;
故答案为,,;
如图即为所求;
平移后的三个顶点坐标分别为:、、;
故答案为,,;
如图,过点A作交y轴于P,
,
,此时.
作点P关于直线BC的对称点,则点也满足条件,此时,
综上所述,满足条件的点P坐标为或.
故答案为或.
12.解:
(1)∵点P(a,b)的对应点为P1(a+6,b-2),
∴平移规律为向右6个单位,向下2个单位,
∴A(-3,3),B(-5,1),C(-2,0)的对应点的坐标为A1(3,1),B1(1,-1),C1(4,-2);
(2)△A1B1C1如图所示;
(3)△AOA1的面积=6×3-×3×3-×3×1-×6×2,
=18---6,
=18-12,
=6.
13.
解:(1)(3,1);(1,2)
(2)解:如图所示,△DEF即为所求. 点E坐标为(0,2),点F坐标为(﹣1,0).
(3)(x﹣4,y﹣1)
(4)将补成长方形,减去3个直角三角形的面积得:
=6-1.5-1-1
=2.5
14.
解:(1)A(1,3); B(2,0);C(3,1);
(2)先向右平移4个单位,再向上平移2个单位;
或:先向上平移2个单位,再向右平移4个单位;
(3)P′(x-4,y-2);
(4)△ABC的面积=2×3-×1×3-×1×1-×2×2
=6-1.5-0.5-2
=2.
第二课时答案
一、单选题
C.D.C.C.C.
二、填空题
6.(1008,0).
7.4.
8.(-1,-3);(-3,-3)
9.(-5,0) (-5,-3) (0,-3)
三、解答题
10.
∴A1(-4,-1),B1(-2,0);
(2)如图所示,则△A2B2C2为所求作的三角形,
11.
(1) 观察图形可知点A(-2,2),点B(-5,-3),点C(0,-1),
所以将三角形ABC向右平移5个单位长度,再向上平移3个单位长度后所得对应点的坐标为:A1(3,5),B1(0,0),C1(5,2);
(2)△A1B1C1如图所示;
(3)△ABC的面积=5×5-×5×2-×2×3-×3×5
=25-5-3-7.5
=25-15.5
=9.5.
12.
解:由题意得,如图所示:
(1)A点到原点的距离是3.
(2)将点C向x轴的负方向平移6个单位,它与点D重合.
(3)直线CE与y轴平行,与x轴垂直;
(4)直线CD与CE垂直,直线CD与FG垂直.
故答案为:(1)3;(2)D;(3)垂直;(4)直线CD与CE垂直,直线CD与FG垂直.
13.
(1) △ABC先向右平移6个单位,再向上平移4个单位得到△A′B′C′或△ABC先向上平移4个单位,再向右平移6个单位得到△A′B′C′
(2) A′(2,3) B′(1,0) C′(5,1);
(3)S△A′B′C′=4×3 ×3×1 ×3×2 ×1×4=12 1.5 3 2=5.5.
14.
解:(1){3,1}+{1,2}={4,3};
{1,2}+{3,1}={4,3}.
(2) 画图如下:
最后的位置仍是B.
(3)从O出发,先向右平移2个单位,再向上平移3个单位,可知平移量为{2,3},
同理得到P到Q的平移量为{3,2},从Q到O的平移量为{-5,-5},故有{2,3}+{3,2}+{-5,-5}={0,0}.
