八年级数学上册试题 15.2线段的垂直平分线-沪科版(含答案)
文档属性
| 名称 | 八年级数学上册试题 15.2线段的垂直平分线-沪科版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 320.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-05 19:51:10 | ||
图片预览




文档简介
15.2线段的垂直平分线
一、单选题
1.如图,在△ABC中,DE垂直平分AC,若BC=20cm,AB=12cm,则△ABD的周长为( )
A.20 cm B.22 cm C.26 cm D.32cm
2.如图,在中,的垂直平分线交于点,交于点,连接.若,,则的周长为( )
A.8 B.11 C.16 D.17
3.下列说法不正确的是( )
A.在角的内部,角平分线上的点到这个角两条边的距离相等
B.线段的垂直平分线上的点到这条线段的两个端点的距离相等
C.圆有无数条对称轴
D.等腰三角形的对称轴是底角的平分线所在的直线
4.如图,△ABC中,AB的垂直平分线DE交AC于D,如果△DBC的周长等于9cm,BC=4cm,那么AC的长是( )
A.5cm B.6cm C.7cm D.9cm
5.如图,在中,的垂直平分线交于点P,已知,则线段的长度为( )
A.8 B.7 C.6 D.5
6.在联欢会上,有、、三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在的( )
A.三边中线的交点 B.三条角平分线的交点
C.三边中垂线的交点 D.三边上高所在直线的交点
7.如图,在△ABC中,AB>AC,按以下步骤作图:分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N,作直线MN交AB于点D,连结CD.若AB=8,AC=3,则△ACD的周长为( )
A.9 B.10 C.11 D.12
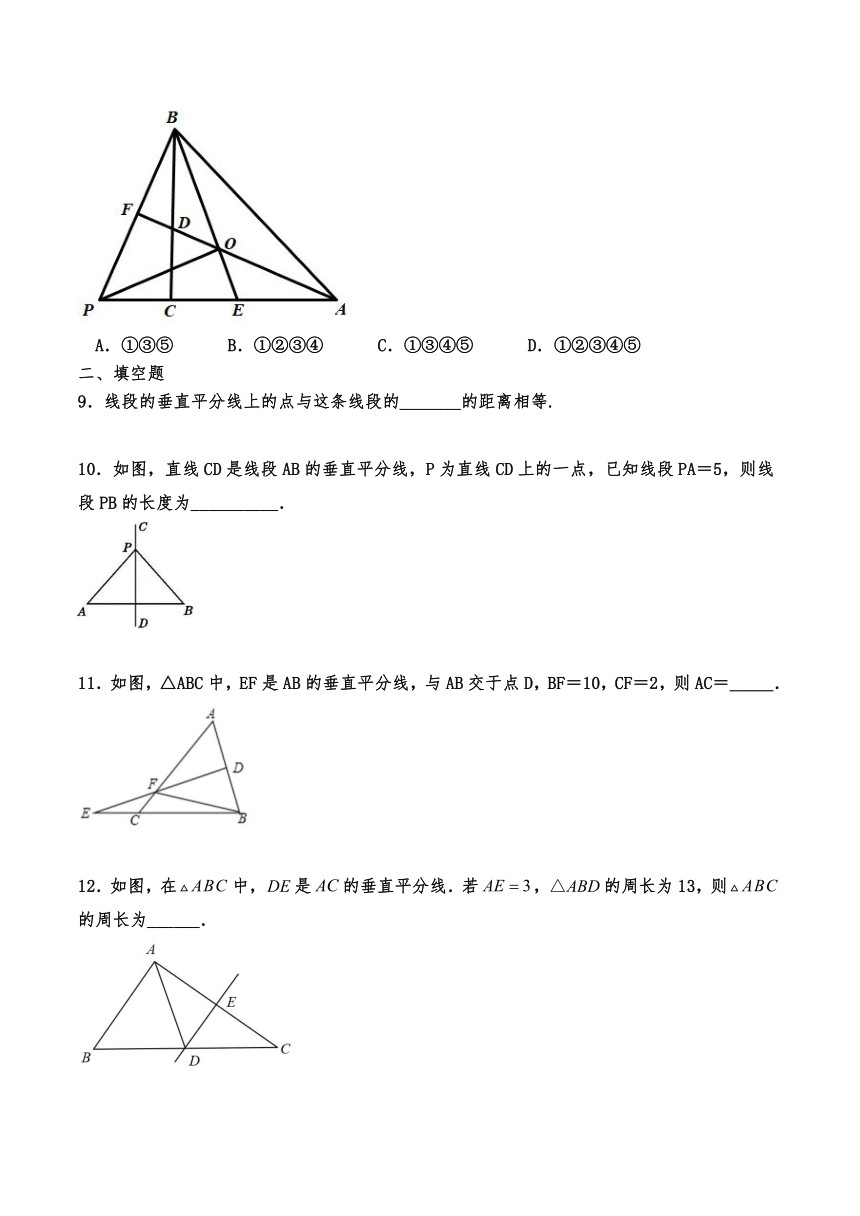
8.如图,在中,,,平分,平分,且交于点O,延长至点P,使,连接;延长交于点F.则下列结论:①:②:③:④;⑤.其中正确的是( )
A.①③⑤ B.①②③④ C.①③④⑤ D.①②③④⑤
二、填空题
9.线段的垂直平分线上的点与这条线段的_______的距离相等.
10.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为__________.
11.如图,△ABC中,EF是AB的垂直平分线,与AB交于点D,BF=10,CF=2,则AC=_____.
12.如图,在中,是的垂直平分线.若,的周长为13,则的周长为______.
13.如图,已知,DE是AB的垂直平分线,,,,则______.
14.如图,在中,,,以为圆心,任意长为半径画弧分别交、于点和,再分别以、为圆心,大于的长为半径画弧,两弧交于点,连结并延长交于点,则下列说法①是的平分线;②;③点在的中垂线上;正确的个数是______个.
三、解答题
15.已知两点A、B和直线l,求作一圆,使之经过A、B两点,且圆心在直线l上.
16.如图,已知四边形ABCD是平行四边形.
(1)用直尺和圆规作出对角线AC的垂直平分线,分别交AD,BC于E,F;(保留作图痕迹,不写作法)
(2)在(1)作出的图形中,连接CE,AF,若AB=4,BC=8,且AB⊥AC,求四边形AECF的周长.
17.如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=6,求△ADE的周长.
(2)若∠DAE=60°,求∠BAC的度数.
18.如图,,的垂直平分线交于,交于.
(1)若,求的度数;
(2)若,的周长17,求的周长.
19.如图,平分,为的中点,且,过点作于点,于点.
(1)求证:;
(2)如果,,求,的长.
20.如图,中,,,、分别为、的垂直平分线,E、G分别为垂足.
(1)求的度数;
(2)若的周长为20,求的长.
答案
一、单选题
D.B.D.A.D.C.C.C.
二、填空题
9.两个端点.
10.5.
11.12.
12.
13.17.
14.3.
三、解答题
15.
解:连接AB,作线段AB的垂直平分线交直线于点O.以点O为圆心,AO为半径作圆,
则⊙O即为所求,
16.
解:(1)如图所示:直线EF即为所求.
(2)由(1)作图可知F是BC的中点,
则FC=BC=4,
∴AE=CF=4,
∵AE∥FC,
∴四边形AECF是平行四边形,
∵AC⊥EF,
∴四边形AECF是菱形,
∴四边形AECF的周长为16.
17.
解:(1)∵在△ABC中,边AB、AC的垂直平分线分别交BC于D、E,
∴DB=DA,EA=EC,
又BC=6,
∴△ADE的周长=AD+DE+EA=BD+DE+EC=BC=6,
(2)∵∠DAE=60°,
∴∠ADE+∠AED=120°
∵DB=DA,EA=EC,
∴∠B=∠BAD,∠C=∠CAE
∴∠ADE=∠B+∠BAD=2∠B,∠AED=∠C+∠CAE=2∠C
∴2∠B+2∠C=120°
∴∠B+∠C=60°
∴∠BAC=180°﹣(∠B+∠C)=120°
18.
(1)∵AB=AC,
∴△ABC是等腰三角形,
∵∠A=40,
∴∠ABC=∠C=×(180 40)=70,
∵DE所在的直线是AB的垂直平分线
∴△ABD是等腰三角形,
∴∠ABD=∠A=40,
∴∠DBC=∠ABC ∠ABD=70 40=30;
(2)∵△ABD是等腰三角形
∴AD=BD,
∵C△CBD=BC+CD+BD=17,
∴BC+CD+AD=BC+AC=17,
∵AE=5
∴AB=2AE=10,
∴C△ABC=AB+BC+AC=10+17=27.
19.
解:(1)证明:连接AM、MC,
∵为的中点,且,
∴AM=MC,
∵平分,,,
∴MF=ME,∠BFM=∠BEM=90°,
∴Rt△AFM≌Rt△CEM(HL),
∴AF=CE;
(2)在Rt△BFM和Rt△BEM中
∵MF=ME,BM=BM,
∴Rt△BFM≌Rt△BEM(HL),
∴BF=BE,
∴,
∵,,
∴,
∵AF=CE,
∴,
∴.
20.
(1)∵,
∴;
∵是线段的垂直平分线,
∴,∴,
同理可得,,
∴;
(2)∵的周长为20,
∴,
由(1)可知,,,
∴.
一、单选题
1.如图,在△ABC中,DE垂直平分AC,若BC=20cm,AB=12cm,则△ABD的周长为( )
A.20 cm B.22 cm C.26 cm D.32cm
2.如图,在中,的垂直平分线交于点,交于点,连接.若,,则的周长为( )
A.8 B.11 C.16 D.17
3.下列说法不正确的是( )
A.在角的内部,角平分线上的点到这个角两条边的距离相等
B.线段的垂直平分线上的点到这条线段的两个端点的距离相等
C.圆有无数条对称轴
D.等腰三角形的对称轴是底角的平分线所在的直线
4.如图,△ABC中,AB的垂直平分线DE交AC于D,如果△DBC的周长等于9cm,BC=4cm,那么AC的长是( )
A.5cm B.6cm C.7cm D.9cm
5.如图,在中,的垂直平分线交于点P,已知,则线段的长度为( )
A.8 B.7 C.6 D.5
6.在联欢会上,有、、三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在的( )
A.三边中线的交点 B.三条角平分线的交点
C.三边中垂线的交点 D.三边上高所在直线的交点
7.如图,在△ABC中,AB>AC,按以下步骤作图:分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N,作直线MN交AB于点D,连结CD.若AB=8,AC=3,则△ACD的周长为( )
A.9 B.10 C.11 D.12
8.如图,在中,,,平分,平分,且交于点O,延长至点P,使,连接;延长交于点F.则下列结论:①:②:③:④;⑤.其中正确的是( )
A.①③⑤ B.①②③④ C.①③④⑤ D.①②③④⑤
二、填空题
9.线段的垂直平分线上的点与这条线段的_______的距离相等.
10.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为__________.
11.如图,△ABC中,EF是AB的垂直平分线,与AB交于点D,BF=10,CF=2,则AC=_____.
12.如图,在中,是的垂直平分线.若,的周长为13,则的周长为______.
13.如图,已知,DE是AB的垂直平分线,,,,则______.
14.如图,在中,,,以为圆心,任意长为半径画弧分别交、于点和,再分别以、为圆心,大于的长为半径画弧,两弧交于点,连结并延长交于点,则下列说法①是的平分线;②;③点在的中垂线上;正确的个数是______个.
三、解答题
15.已知两点A、B和直线l,求作一圆,使之经过A、B两点,且圆心在直线l上.
16.如图,已知四边形ABCD是平行四边形.
(1)用直尺和圆规作出对角线AC的垂直平分线,分别交AD,BC于E,F;(保留作图痕迹,不写作法)
(2)在(1)作出的图形中,连接CE,AF,若AB=4,BC=8,且AB⊥AC,求四边形AECF的周长.
17.如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=6,求△ADE的周长.
(2)若∠DAE=60°,求∠BAC的度数.
18.如图,,的垂直平分线交于,交于.
(1)若,求的度数;
(2)若,的周长17,求的周长.
19.如图,平分,为的中点,且,过点作于点,于点.
(1)求证:;
(2)如果,,求,的长.
20.如图,中,,,、分别为、的垂直平分线,E、G分别为垂足.
(1)求的度数;
(2)若的周长为20,求的长.
答案
一、单选题
D.B.D.A.D.C.C.C.
二、填空题
9.两个端点.
10.5.
11.12.
12.
13.17.
14.3.
三、解答题
15.
解:连接AB,作线段AB的垂直平分线交直线于点O.以点O为圆心,AO为半径作圆,
则⊙O即为所求,
16.
解:(1)如图所示:直线EF即为所求.
(2)由(1)作图可知F是BC的中点,
则FC=BC=4,
∴AE=CF=4,
∵AE∥FC,
∴四边形AECF是平行四边形,
∵AC⊥EF,
∴四边形AECF是菱形,
∴四边形AECF的周长为16.
17.
解:(1)∵在△ABC中,边AB、AC的垂直平分线分别交BC于D、E,
∴DB=DA,EA=EC,
又BC=6,
∴△ADE的周长=AD+DE+EA=BD+DE+EC=BC=6,
(2)∵∠DAE=60°,
∴∠ADE+∠AED=120°
∵DB=DA,EA=EC,
∴∠B=∠BAD,∠C=∠CAE
∴∠ADE=∠B+∠BAD=2∠B,∠AED=∠C+∠CAE=2∠C
∴2∠B+2∠C=120°
∴∠B+∠C=60°
∴∠BAC=180°﹣(∠B+∠C)=120°
18.
(1)∵AB=AC,
∴△ABC是等腰三角形,
∵∠A=40,
∴∠ABC=∠C=×(180 40)=70,
∵DE所在的直线是AB的垂直平分线
∴△ABD是等腰三角形,
∴∠ABD=∠A=40,
∴∠DBC=∠ABC ∠ABD=70 40=30;
(2)∵△ABD是等腰三角形
∴AD=BD,
∵C△CBD=BC+CD+BD=17,
∴BC+CD+AD=BC+AC=17,
∵AE=5
∴AB=2AE=10,
∴C△ABC=AB+BC+AC=10+17=27.
19.
解:(1)证明:连接AM、MC,
∵为的中点,且,
∴AM=MC,
∵平分,,,
∴MF=ME,∠BFM=∠BEM=90°,
∴Rt△AFM≌Rt△CEM(HL),
∴AF=CE;
(2)在Rt△BFM和Rt△BEM中
∵MF=ME,BM=BM,
∴Rt△BFM≌Rt△BEM(HL),
∴BF=BE,
∴,
∵,,
∴,
∵AF=CE,
∴,
∴.
20.
(1)∵,
∴;
∵是线段的垂直平分线,
∴,∴,
同理可得,,
∴;
(2)∵的周长为20,
∴,
由(1)可知,,,
∴.
