八年级数学上册试题 15.3 等腰三角形 -沪科版(含答案)
文档属性
| 名称 | 八年级数学上册试题 15.3 等腰三角形 -沪科版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 817.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-05 00:00:00 | ||
图片预览




文档简介
15.3 等腰三角形
第1课时 等腰三角形的性质定理及推论
一、单选题
1.已知等腰三角形的两边长为和.且、满足,则这个三角形的三边长分别是( )
A.7,7,3 B.3,3,7 C.7,7,3或3,3,7 D.无法计算
2.如图,在中AB=AC,BC=4,面积是20,AC的垂直平分线EF分别交AC、AB边于E、F点,若点D为BC边的中点,点M为线段上一动点,则周长的最小值为( )
A.6 B.8 C.10 D.12
3.如图,在中,,的平分线与的中垂线交于点O,连接,则的度数为( )
A. B. C. D.
4.如图,在中,,,的垂直平分线交于点D,交于点E,则的度数为( )
A.70° B.40° C.35° D.30°
5.已知△ABC的周长为m,BC=m-2AB,则下列直线一定为△ABC的对称轴的是( )
A.△ABC的边BC上的中线所在的直线 B.∠ACB的平分线所在的直线
C.△ABC的边AB的垂直平分线 D.△ABC的边AC上的高所在的直线
6.等腰三角形的顶角为50°,则它的底角是( ).
A.50° B.65° C.70° D.75°
7.若一个等腰三角形的两边长分别为 ,,则三角形的周长为( )
A. B. C. D.或
8.等腰三角形的顶角为 80°,则它的底角为( )
A.100° B.80° C.50° D.50°或 80°
二、填空题
9.如图,已知和均为等边三角形,点O是的中点,点D在射线上,连结,则_________,若,则的最小值=_________.
10.如图,∠AOC=∠BOC=15°,CF∥OA,CE⊥OA于点E,若CF=16,则CE=________.
11.我们规定:等腰三角形的顶角与一个底角度数的比值叫作等腰三角形的“特征值”,记作.若则该等腰三角形的顶角为_______________.
12.如图①是一张Rt△ABC纸片,如果用两张相同的这种纸片恰好能拼成一个正三角形,如图②,那么在Rt△ABC中,BC=6,则AB=_____.
13.等腰三角形两边长分别是3和6,则该三角形的周长为_________.
14.中,,则______.
三、解答题
15.已知一个等腰三角形的周长是12cm,其中一边长是2cm,求另外两边的长.
16.如图,已知的交点为,;过点作,垂足为.
(1)求证:△≌△
(2)求证:为边的中点.
17.已知等腰三角形的周长是16cm.
(1)若其中一边长为4cm,求另外两边的长;
(2)若其中一边长为6cm,求另外两边长;
18.如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD//BE,∠GBE的平分线与AD交于点D,连接CD.
(1)求证:①AB=AD;②CD平分∠ACE.
(2)猜想∠BDC与∠BAC之间有何数量关系?并对你的猜想加以证明.
19.我们定义:如图1,在中,把绕点A顺时针旋转得到,把绕点A逆时针旋转得到,连接.当时,我们称是的“旋补三角形”, 边上的中线叫做的“旋补中线”,点A叫做“旋补中心”.
特例感知:(1)在图2,图3中,是的“旋补三角形”,是的“旋补中线”.
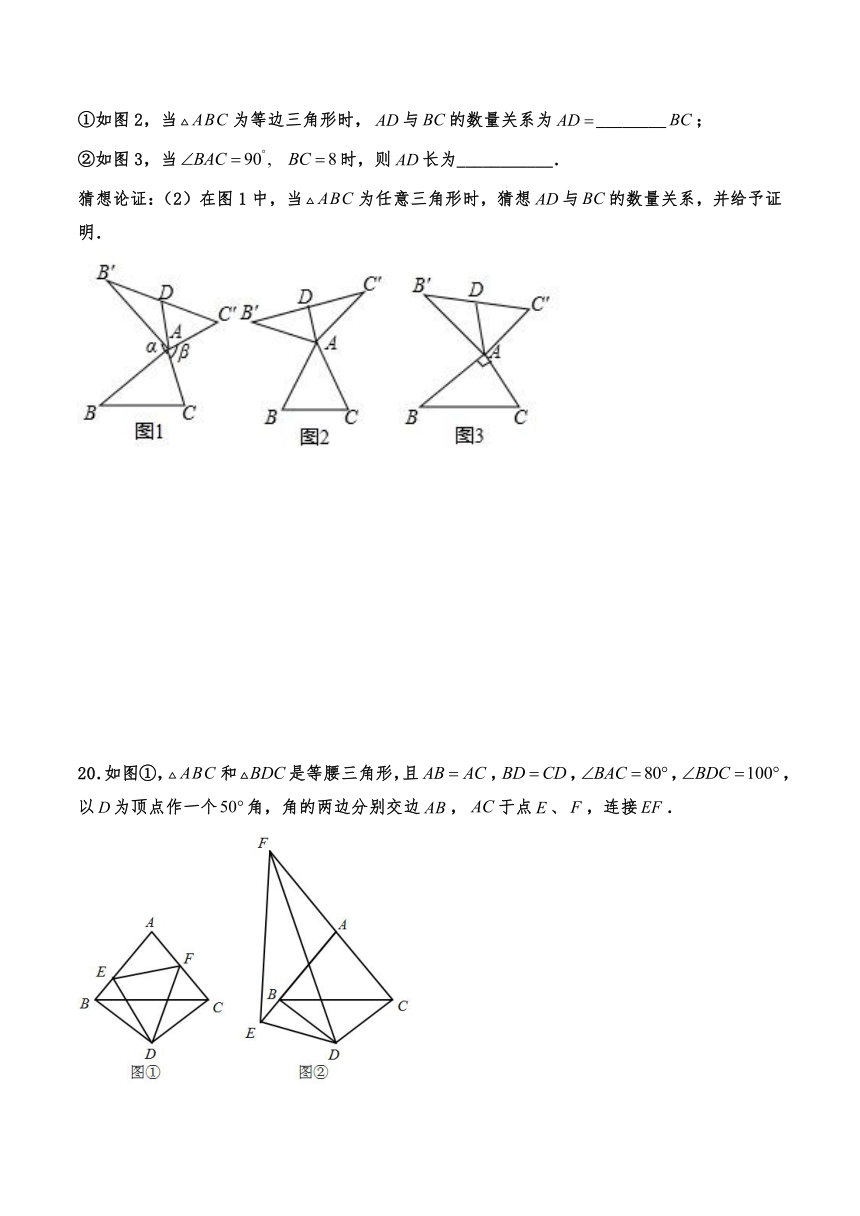
①如图2,当为等边三角形时,与的数量关系为________;
②如图3,当时,则长为___________.
猜想论证:(2)在图1中,当为任意三角形时,猜想与的数量关系,并给予证明.
20.如图①,和是等腰三角形,且,,,,以为顶点作一个角,角的两边分别交边,于点、,连接.
(1)探究、、之间的关系,并说明理由;
(2)若点、分别在、CA延长线上,其他条件不变,如图②所示,则、、之间存在什么样的关系?并说明理由.
第2课时 等腰三角形的判定定理及推论
一、单选题
1.已知一个等腰三角形的一个内角是80°,则它的顶角为()
A.20° B.50° C.40° D.20°或80°
2.如图,平分∠,∠=15°,∥,⊥于点,=4,则=( ).
A.2 B.2.5 C.3 D.3.5
3.等腰三角形的周长为,其中一边长为,则该等腰三角形的底边长为( )
A.或 B.或 C. D.
4.在△ABC中,其两个内角如下,则能判定△ABC为等腰三角形的是( )
A.∠A=40°,∠B=50 B.∠A=40°,∠B=60°
C.∠A=40°,∠B=70 D.∠A=40°,∠B=80°
5.如图所示,在中,,,且,则的度数为( )
A.22.5° B.45° C.36° D.25°
6.如图所示,射线BA、CA交于点A,连接BC,已知AB=AC,∠B=40°,那么x的值是( )
A.100 B.40 C.55 D.80
7.如图,在中,和的平分线交于点,过点作交于交于,若则线段的长为( )
A. B. C. D.
8.如图,等腰三角形的底边长为4,面积为12,腰的垂直平分线分别交、于点、,若点为底边的中点,点为线段上一动点,则的周长的最小值为( )
A.7 B.8 C.9 D.10
二、填空题
9.等腰△ABC周长为18cm,其中两边长的差为3cm,则腰长为_____.
10.由坐标平面内的三点,,构成的是________三角形.
11.如图,以的顶点为圆心,长为半径画弧,交边于点,连接,若,,则的大小为_________度.
12.如图,在中,,,平分,交于点,若,则______________.
13.如图,在△ABC中,,,,,,则_____
14.如图,在锐角中,,点为边上的一定点,连接,,,分别为边和上的两动点,连接,,,则周长的最小值为______;当周长的最小值时, 的度数为______.
三、解答题
15.如图,在△ABC中,AB=BC,∠ABC=90°,点E在BC上,点F在AB的延长线上,且AE=CF.
(1)求证:△ABE≌△CBF.
(2)若∠ACF=70°,求∠EAC的度数.
16.如图,是等边三角形,点是的中点,,过点作,垂足为,的反向延长线交于点.
(1)求证:;
(2)求证:垂直平分.
17.已知中,,为边上的高,平分,分别交、于点、.求证:.
18.如图1,AD∥BC,AB ⊥BC于B,∠DCB=75°,以CD为边的等边△DCE的另一顶点E在线段AB上.
(1)填空:∠ADE=____°;
(2)求证: AB=BC;
(3)如图2所示,若F为线段CD上一点,∠FBC=30°,求的值.
19.在△ABC中,∠ABC=45°,F是高AD与高BE的交点.
(1)求证:△ADC≌△BDF.
(2)连接CF,若CD=4,求CF的长.
20.在等边三角形中,点在边上,点在的延长线上,且.
(1)如图1,当为中点时,求证:;
(2)如图2,若,,求.
第1课时答案
一、单选题
A.D.A.D.A.B. C.C.
二、填空题
9..
10.8.
11.108°.
12.12.
13.15.
14.50°
三、解答题
15.
解:(1)若该等腰三角形的腰长为,则另外两边的长为,,
根据三角形三边关系∵2+2=4<8,故不能构成三角形;
(2)若等腰三角形的底边长为,则腰长为,
即另外两边的长为,,能构成三角形;
综上所述,该等腰三角形的另外两边的长为,.
故答案为:,.
16.
证明:(1)在和中
∴△≌△ .
(2)∵△≌△
∴
又∵
∴为△的中线 (三线合一)
即F为BC边的中点
17.
(1)如果腰长为4cm,则底边长为16-4-4=8cm.
∴等腰三角形的三边长为4cm,4cm,8cm,
又∵4+4=8,
∴不符合三角形三边关系定理.
∴应该是底边长为4cm.
∴腰长为(16-4)÷2=6cm.
∴等腰三角形的三边长为4cm,6cm,6cm,
又∵4+6>6,符合三角形三边关系定理,
∴另外两边长都为6cm;
综合上述可得,另外两边分别为6cm、6cm.
(2)如果腰长为6cm,则底边长为16-6-6=4cm.
∴等腰三角形的三边长为4cm,6cm,6cm,
又∵4+6>6,符合三角形三边关系定理.
∴另外两边长分别为6cm和4cm.
如果底边长为6cm,则腰长为(16-6)÷2=5cm.
∴等腰三角形的三边长为6cm,5cm,5cm,
又∵5+5>6,符合三角形三边关系定理,
∴另外两边长都为5cm.
综合上述可得另外两边长分别为6cm、4cm或5cm、5cm.
18.
(1)证明:平分
∴∠ABD=∠DBC
∴∠ADB=∠DBC
∴∠ABD=∠ADB,
;
②,
平分
(2)
理由:∵CD、BD分别平分∠ACE,∠ABE,
,∠DBC=∠ABC,
又
又∵∠BDC+∠DBC=∠DCE
∴∠BDC+∠ABC=∠ACE,
∴∠BDC+∠ABC=∠ABC+∠BAC,
∴.
19.
(1)①∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=60°,
∵△AB′C′是△ABC的“旋补三角形”,
∴∠B′AC′=120°,AB=AB′,AC=AC′,
∴AB′=AC′,
∴∠AB′D=30°,
∴AD=AB′,
∴AD=BC,
故答案为;
②∵△AB′C′是△ABC的“旋补三角形”,
∴∠B′AC′=∠BAC=90°,AB=AB′,AC=AC′,
在△AB′C′和△ABC中,
,
∴△AB′C′≌△ABC(SAS)
∴B′C′=BC=8,
∵∠B′AC′=90°,AD是△ABC的“旋补中线”,
∴AD=B′C′=4,
故答案为4;
(2)猜想.
证明:如图,延长至点E使得,连接B′E、C′E,
∵AD是△AB′C’的中线,
∴B′D=C′D,
∵DE=AD,
∴四边形AB′EC′是平行四边形,
∴B′E=AC′,∠B′AC′+∠AB′E=180°,
∵α+β=180°,
∴∠B′AC′+∠BAC=180°,
∴∠EB′A=∠BAC,
在△EB′A和△CAB中,
∴△EB′A≌△CAB(SAS),
∴AE=BC,
∴AD=BC.
20.
(1)和是等腰三角形,
延长AB至G,使得BG=CF,连接DG
在和中,
BG=CF,
,
在和中,
DE=DE,
,
(2)在CA上截取CG=BE,连接DG
是等腰三角形,
在和中,
CG=BE,
在和中,
FD=FD,
第2课时答案
一、单选题
D.A.A.C.B.D.A.B.
二、填空题
9.5cm或7cm.
10.等腰直角.
11.80.
12.2.
13.11.
14.4,120°.
三、解答题
15.
证明:∵∠ABC=90°
∴△ABE与△CBF为直角三角形.
∵在Rt△ABE与Rt△BCF中,
,
∴Rt△ABE≌Rt△CBF;
(2)∵AB=BC,∠ABC=90°,
∴∠BAC=∠ACB=45°,
∵∠ACF=70°,
∴∠FBC=25°,
由Rt△ABE≌Rt△CBF,∴∠EAB=∠FBC=25°,
∴∠EAC=20°.
16.
证明:(1)∵点是的中点
∴
∵
∴
在和中
∴≌
∴
∴
∴
(2)∵点是等边中边的中点
∴且平分
∴,
∵
∴
∴
∴是等腰三角形
又∵
∴是中边的中线
又
∴垂直平分.
17.
解析∵,
∴,
∵为边上的高,
∴,
∴,
∴,
∵是的平分线,
∴,
∴,
∵,
∴,
∴.
18.
解:(1)∵∠DCB=75°,AD∥BC,
∴∠ADC=105°
∵△DCE为等边三角形,
∴∠EDC=60°,
∴∠ADE=∠ADC-∠EDC=45°.
(2)证明:连接AC
由(1)知∠ADE =45 ,
∵AB⊥BC,AD∥BC,
∴∠DAB=90 ,
∴∠AED=45 ,
∴AD=AE,
∴点A在线段DE的垂直平分线上,
∵△DCE为等边三角形,
∴CD=CE,
∴点C也在线段DE的垂直平分线上 ,
∴AC就是线段DE的垂直平分线,
即AC⊥DE,
∴AC平分∠EAD,
∴∠BAC=45°,
∴△ABC是等腰直角三角形
∴BA=BC
(3)解:连接AF,延长BF交AD的延长线于点G
∵∠FBC=30 ,∠ABC=90 ,
∴∠ABF=60 ,
∵∠DCB=75 ,
∴∠BFC=75 ,
故BC=BF,
由(2)知:BA=BC,
∴BA=BF,
∴△ABF是等边三角形,
∴AB=BF=FA,
∴∠BAC=60 ,
∴∠DAF=30 ,
又∵AD∥BC,
∴∠FAG=∠G=30 ,
∴FG =FA= FB,
又∠DFG=∠CFB,
∴△BCF≌△GDF(ASA),
∴DF=CF,
∴=1.
19.
(1)证明:∵AD⊥BC,
∴∠FDB=∠ADC=90°,
∵∠ABC=45°,
∴∠BAD=45°=∠ABD,
∴AD=BD,
∵BE⊥AC,
∴∠AEF=∠FDB=90°,
∵∠AFE=∠BFD,
∴由三角形内角和定理得:∠CAD=∠FBD,
在△ADC和△BDE中
∴△ADC≌△BDE(ASA);
(2)解:∵△ADC≌△BDE,CD=4,
∴DF=CD=4,
在Rt△FDC中,由勾股定理得:CF===4.
20.
(1)当为中点时,在等边三角形中,
由“三线合一”知:,,
又,,
,
,
,,
在中:,
;
(2)如图,作于点,
,,,
在中,,
,,
又,,
,为等腰三角形,
由“三线合一”知:,
.
第1课时 等腰三角形的性质定理及推论
一、单选题
1.已知等腰三角形的两边长为和.且、满足,则这个三角形的三边长分别是( )
A.7,7,3 B.3,3,7 C.7,7,3或3,3,7 D.无法计算
2.如图,在中AB=AC,BC=4,面积是20,AC的垂直平分线EF分别交AC、AB边于E、F点,若点D为BC边的中点,点M为线段上一动点,则周长的最小值为( )
A.6 B.8 C.10 D.12
3.如图,在中,,的平分线与的中垂线交于点O,连接,则的度数为( )
A. B. C. D.
4.如图,在中,,,的垂直平分线交于点D,交于点E,则的度数为( )
A.70° B.40° C.35° D.30°
5.已知△ABC的周长为m,BC=m-2AB,则下列直线一定为△ABC的对称轴的是( )
A.△ABC的边BC上的中线所在的直线 B.∠ACB的平分线所在的直线
C.△ABC的边AB的垂直平分线 D.△ABC的边AC上的高所在的直线
6.等腰三角形的顶角为50°,则它的底角是( ).
A.50° B.65° C.70° D.75°
7.若一个等腰三角形的两边长分别为 ,,则三角形的周长为( )
A. B. C. D.或
8.等腰三角形的顶角为 80°,则它的底角为( )
A.100° B.80° C.50° D.50°或 80°
二、填空题
9.如图,已知和均为等边三角形,点O是的中点,点D在射线上,连结,则_________,若,则的最小值=_________.
10.如图,∠AOC=∠BOC=15°,CF∥OA,CE⊥OA于点E,若CF=16,则CE=________.
11.我们规定:等腰三角形的顶角与一个底角度数的比值叫作等腰三角形的“特征值”,记作.若则该等腰三角形的顶角为_______________.
12.如图①是一张Rt△ABC纸片,如果用两张相同的这种纸片恰好能拼成一个正三角形,如图②,那么在Rt△ABC中,BC=6,则AB=_____.
13.等腰三角形两边长分别是3和6,则该三角形的周长为_________.
14.中,,则______.
三、解答题
15.已知一个等腰三角形的周长是12cm,其中一边长是2cm,求另外两边的长.
16.如图,已知的交点为,;过点作,垂足为.
(1)求证:△≌△
(2)求证:为边的中点.
17.已知等腰三角形的周长是16cm.
(1)若其中一边长为4cm,求另外两边的长;
(2)若其中一边长为6cm,求另外两边长;
18.如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD//BE,∠GBE的平分线与AD交于点D,连接CD.
(1)求证:①AB=AD;②CD平分∠ACE.
(2)猜想∠BDC与∠BAC之间有何数量关系?并对你的猜想加以证明.
19.我们定义:如图1,在中,把绕点A顺时针旋转得到,把绕点A逆时针旋转得到,连接.当时,我们称是的“旋补三角形”, 边上的中线叫做的“旋补中线”,点A叫做“旋补中心”.
特例感知:(1)在图2,图3中,是的“旋补三角形”,是的“旋补中线”.
①如图2,当为等边三角形时,与的数量关系为________;
②如图3,当时,则长为___________.
猜想论证:(2)在图1中,当为任意三角形时,猜想与的数量关系,并给予证明.
20.如图①,和是等腰三角形,且,,,,以为顶点作一个角,角的两边分别交边,于点、,连接.
(1)探究、、之间的关系,并说明理由;
(2)若点、分别在、CA延长线上,其他条件不变,如图②所示,则、、之间存在什么样的关系?并说明理由.
第2课时 等腰三角形的判定定理及推论
一、单选题
1.已知一个等腰三角形的一个内角是80°,则它的顶角为()
A.20° B.50° C.40° D.20°或80°
2.如图,平分∠,∠=15°,∥,⊥于点,=4,则=( ).
A.2 B.2.5 C.3 D.3.5
3.等腰三角形的周长为,其中一边长为,则该等腰三角形的底边长为( )
A.或 B.或 C. D.
4.在△ABC中,其两个内角如下,则能判定△ABC为等腰三角形的是( )
A.∠A=40°,∠B=50 B.∠A=40°,∠B=60°
C.∠A=40°,∠B=70 D.∠A=40°,∠B=80°
5.如图所示,在中,,,且,则的度数为( )
A.22.5° B.45° C.36° D.25°
6.如图所示,射线BA、CA交于点A,连接BC,已知AB=AC,∠B=40°,那么x的值是( )
A.100 B.40 C.55 D.80
7.如图,在中,和的平分线交于点,过点作交于交于,若则线段的长为( )
A. B. C. D.
8.如图,等腰三角形的底边长为4,面积为12,腰的垂直平分线分别交、于点、,若点为底边的中点,点为线段上一动点,则的周长的最小值为( )
A.7 B.8 C.9 D.10
二、填空题
9.等腰△ABC周长为18cm,其中两边长的差为3cm,则腰长为_____.
10.由坐标平面内的三点,,构成的是________三角形.
11.如图,以的顶点为圆心,长为半径画弧,交边于点,连接,若,,则的大小为_________度.
12.如图,在中,,,平分,交于点,若,则______________.
13.如图,在△ABC中,,,,,,则_____
14.如图,在锐角中,,点为边上的一定点,连接,,,分别为边和上的两动点,连接,,,则周长的最小值为______;当周长的最小值时, 的度数为______.
三、解答题
15.如图,在△ABC中,AB=BC,∠ABC=90°,点E在BC上,点F在AB的延长线上,且AE=CF.
(1)求证:△ABE≌△CBF.
(2)若∠ACF=70°,求∠EAC的度数.
16.如图,是等边三角形,点是的中点,,过点作,垂足为,的反向延长线交于点.
(1)求证:;
(2)求证:垂直平分.
17.已知中,,为边上的高,平分,分别交、于点、.求证:.
18.如图1,AD∥BC,AB ⊥BC于B,∠DCB=75°,以CD为边的等边△DCE的另一顶点E在线段AB上.
(1)填空:∠ADE=____°;
(2)求证: AB=BC;
(3)如图2所示,若F为线段CD上一点,∠FBC=30°,求的值.
19.在△ABC中,∠ABC=45°,F是高AD与高BE的交点.
(1)求证:△ADC≌△BDF.
(2)连接CF,若CD=4,求CF的长.
20.在等边三角形中,点在边上,点在的延长线上,且.
(1)如图1,当为中点时,求证:;
(2)如图2,若,,求.
第1课时答案
一、单选题
A.D.A.D.A.B. C.C.
二、填空题
9..
10.8.
11.108°.
12.12.
13.15.
14.50°
三、解答题
15.
解:(1)若该等腰三角形的腰长为,则另外两边的长为,,
根据三角形三边关系∵2+2=4<8,故不能构成三角形;
(2)若等腰三角形的底边长为,则腰长为,
即另外两边的长为,,能构成三角形;
综上所述,该等腰三角形的另外两边的长为,.
故答案为:,.
16.
证明:(1)在和中
∴△≌△ .
(2)∵△≌△
∴
又∵
∴为△的中线 (三线合一)
即F为BC边的中点
17.
(1)如果腰长为4cm,则底边长为16-4-4=8cm.
∴等腰三角形的三边长为4cm,4cm,8cm,
又∵4+4=8,
∴不符合三角形三边关系定理.
∴应该是底边长为4cm.
∴腰长为(16-4)÷2=6cm.
∴等腰三角形的三边长为4cm,6cm,6cm,
又∵4+6>6,符合三角形三边关系定理,
∴另外两边长都为6cm;
综合上述可得,另外两边分别为6cm、6cm.
(2)如果腰长为6cm,则底边长为16-6-6=4cm.
∴等腰三角形的三边长为4cm,6cm,6cm,
又∵4+6>6,符合三角形三边关系定理.
∴另外两边长分别为6cm和4cm.
如果底边长为6cm,则腰长为(16-6)÷2=5cm.
∴等腰三角形的三边长为6cm,5cm,5cm,
又∵5+5>6,符合三角形三边关系定理,
∴另外两边长都为5cm.
综合上述可得另外两边长分别为6cm、4cm或5cm、5cm.
18.
(1)证明:平分
∴∠ABD=∠DBC
∴∠ADB=∠DBC
∴∠ABD=∠ADB,
;
②,
平分
(2)
理由:∵CD、BD分别平分∠ACE,∠ABE,
,∠DBC=∠ABC,
又
又∵∠BDC+∠DBC=∠DCE
∴∠BDC+∠ABC=∠ACE,
∴∠BDC+∠ABC=∠ABC+∠BAC,
∴.
19.
(1)①∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=60°,
∵△AB′C′是△ABC的“旋补三角形”,
∴∠B′AC′=120°,AB=AB′,AC=AC′,
∴AB′=AC′,
∴∠AB′D=30°,
∴AD=AB′,
∴AD=BC,
故答案为;
②∵△AB′C′是△ABC的“旋补三角形”,
∴∠B′AC′=∠BAC=90°,AB=AB′,AC=AC′,
在△AB′C′和△ABC中,
,
∴△AB′C′≌△ABC(SAS)
∴B′C′=BC=8,
∵∠B′AC′=90°,AD是△ABC的“旋补中线”,
∴AD=B′C′=4,
故答案为4;
(2)猜想.
证明:如图,延长至点E使得,连接B′E、C′E,
∵AD是△AB′C’的中线,
∴B′D=C′D,
∵DE=AD,
∴四边形AB′EC′是平行四边形,
∴B′E=AC′,∠B′AC′+∠AB′E=180°,
∵α+β=180°,
∴∠B′AC′+∠BAC=180°,
∴∠EB′A=∠BAC,
在△EB′A和△CAB中,
∴△EB′A≌△CAB(SAS),
∴AE=BC,
∴AD=BC.
20.
(1)和是等腰三角形,
延长AB至G,使得BG=CF,连接DG
在和中,
BG=CF,
,
在和中,
DE=DE,
,
(2)在CA上截取CG=BE,连接DG
是等腰三角形,
在和中,
CG=BE,
在和中,
FD=FD,
第2课时答案
一、单选题
D.A.A.C.B.D.A.B.
二、填空题
9.5cm或7cm.
10.等腰直角.
11.80.
12.2.
13.11.
14.4,120°.
三、解答题
15.
证明:∵∠ABC=90°
∴△ABE与△CBF为直角三角形.
∵在Rt△ABE与Rt△BCF中,
,
∴Rt△ABE≌Rt△CBF;
(2)∵AB=BC,∠ABC=90°,
∴∠BAC=∠ACB=45°,
∵∠ACF=70°,
∴∠FBC=25°,
由Rt△ABE≌Rt△CBF,∴∠EAB=∠FBC=25°,
∴∠EAC=20°.
16.
证明:(1)∵点是的中点
∴
∵
∴
在和中
∴≌
∴
∴
∴
(2)∵点是等边中边的中点
∴且平分
∴,
∵
∴
∴
∴是等腰三角形
又∵
∴是中边的中线
又
∴垂直平分.
17.
解析∵,
∴,
∵为边上的高,
∴,
∴,
∴,
∵是的平分线,
∴,
∴,
∵,
∴,
∴.
18.
解:(1)∵∠DCB=75°,AD∥BC,
∴∠ADC=105°
∵△DCE为等边三角形,
∴∠EDC=60°,
∴∠ADE=∠ADC-∠EDC=45°.
(2)证明:连接AC
由(1)知∠ADE =45 ,
∵AB⊥BC,AD∥BC,
∴∠DAB=90 ,
∴∠AED=45 ,
∴AD=AE,
∴点A在线段DE的垂直平分线上,
∵△DCE为等边三角形,
∴CD=CE,
∴点C也在线段DE的垂直平分线上 ,
∴AC就是线段DE的垂直平分线,
即AC⊥DE,
∴AC平分∠EAD,
∴∠BAC=45°,
∴△ABC是等腰直角三角形
∴BA=BC
(3)解:连接AF,延长BF交AD的延长线于点G
∵∠FBC=30 ,∠ABC=90 ,
∴∠ABF=60 ,
∵∠DCB=75 ,
∴∠BFC=75 ,
故BC=BF,
由(2)知:BA=BC,
∴BA=BF,
∴△ABF是等边三角形,
∴AB=BF=FA,
∴∠BAC=60 ,
∴∠DAF=30 ,
又∵AD∥BC,
∴∠FAG=∠G=30 ,
∴FG =FA= FB,
又∠DFG=∠CFB,
∴△BCF≌△GDF(ASA),
∴DF=CF,
∴=1.
19.
(1)证明:∵AD⊥BC,
∴∠FDB=∠ADC=90°,
∵∠ABC=45°,
∴∠BAD=45°=∠ABD,
∴AD=BD,
∵BE⊥AC,
∴∠AEF=∠FDB=90°,
∵∠AFE=∠BFD,
∴由三角形内角和定理得:∠CAD=∠FBD,
在△ADC和△BDE中
∴△ADC≌△BDE(ASA);
(2)解:∵△ADC≌△BDE,CD=4,
∴DF=CD=4,
在Rt△FDC中,由勾股定理得:CF===4.
20.
(1)当为中点时,在等边三角形中,
由“三线合一”知:,,
又,,
,
,
,,
在中:,
;
(2)如图,作于点,
,,,
在中,,
,,
又,,
,为等腰三角形,
由“三线合一”知:,
.
