第二十二章 二次函数 单元复习课件(69张PPT)
文档属性
| 名称 | 第二十二章 二次函数 单元复习课件(69张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 9.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-07 09:25:36 | ||
图片预览








文档简介
(共69张PPT)
学习目标
1 掌握二次函数的概念,并能根据二次函数的图像与性质解决相关问题。
2 掌握用待定系数法求抛物线解析式的方法。
3 能够利用二次函数解决有关实际问题,能根据具体问题的实际意义检验结果的合理性,进一步培养学生分析问题、解决问题的意识和能力。
本章重点内容:
1 掌握二次函数的图象特征及其性质;
2 掌握用待定系数法求抛物线解析式的方法。
本章难点内容:
1 理解二次函数与一元二次方程的关系;
2 利用二次函数解决实际问题。
二次函数是初中阶段函数中的重要函数,它在解决各类数学问题和实际问题中有着广泛的应用。掌握二次函数图象和性质是学习二次函数的基础,根据二次函数图象判断抛物线抛的开口方向,顶点坐标,对称轴,与坐标轴交点坐标、确定二次函数的解析式为必须掌握内容,理解二次函数与各系数之间的关系,灵活运用二次函数解决实际问题。二次函数是体现综合性的重点内容,在期中期末试卷中即有相对稳定的基础题,也有新颖的试题来考查学生的分析,解决问题能力,实践和创新能力,因此经常与一次函数,三角形,四边形知识结合在一起,成为试卷的压轴题。
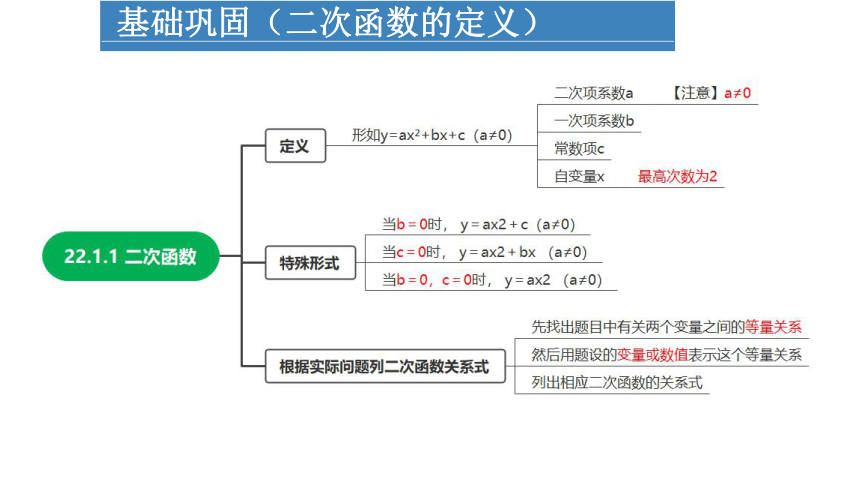
基础巩固(二次函数的定义)
一般地,形如y=ax +bx+c(其中a、b、c是常数,a≠0)的函数叫做二次函数。其中,x是自变量,a、b、c分别是函数解析式的二次项系数、一次项系数和常数项。
【提问】同学们,谈谈你对二次函数的理解,需要注意些什么?
1)含有一个自变量,且自变量的最高次数为2。
2)二次项系数不等于0。
3)等式两边都是整式。
4)一般情况下,自变量x的取值范围是任意实数。
基础巩固(二次函数的定义)
二次函数的特殊形式:
基础巩固(二次函数的定义)
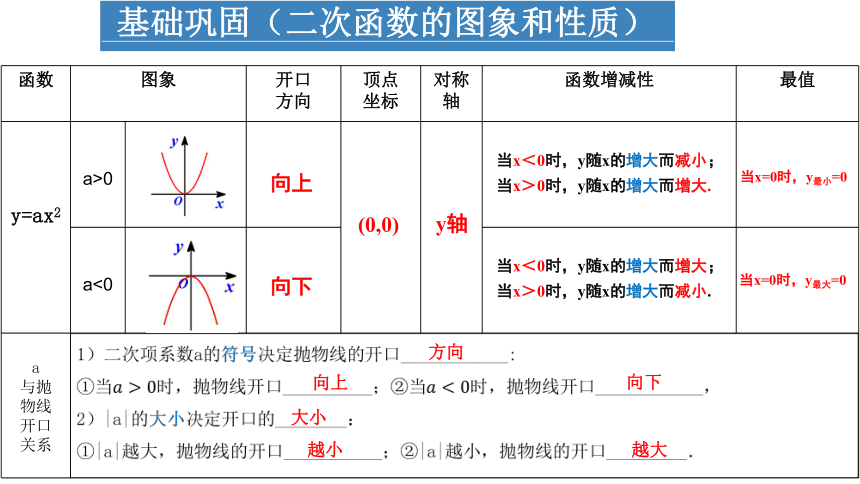
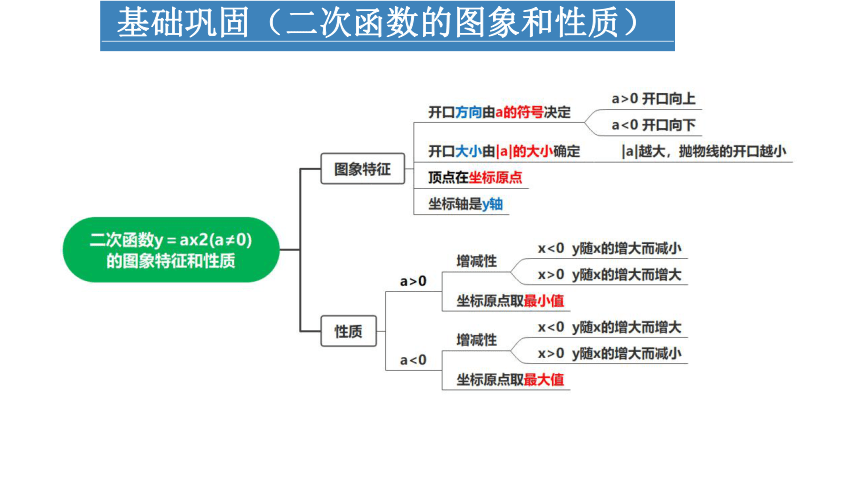
基础巩固(二次函数的图象和性质)
向上
向下
(0,0)
y轴
当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.
当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小.
当x=0时,y最小=0
当x=0时,y最大=0
方向
向上
向下
大小
越小
越大
基础巩固(二次函数的图象和性质)
二次函数y=ax2 中比较函数值的大小的方法:
方法 步骤 适用范围
直接代入法 将x的值分别代入到函数解析式中,
求出y值再比较大小 多用于a值确定
性质判断法 结合二次函数的性质(增减性)及自变量x之间的大小关系,得出其对应y值的大小关系 多用于自变量x在对称轴同一侧的情况
草图法 画出二次函数的草图并描点,
根据图象直接判断y值的大小 多用于a值不确定且x值不在对称轴同侧的情况
基础巩固(二次函数的图象和性质)
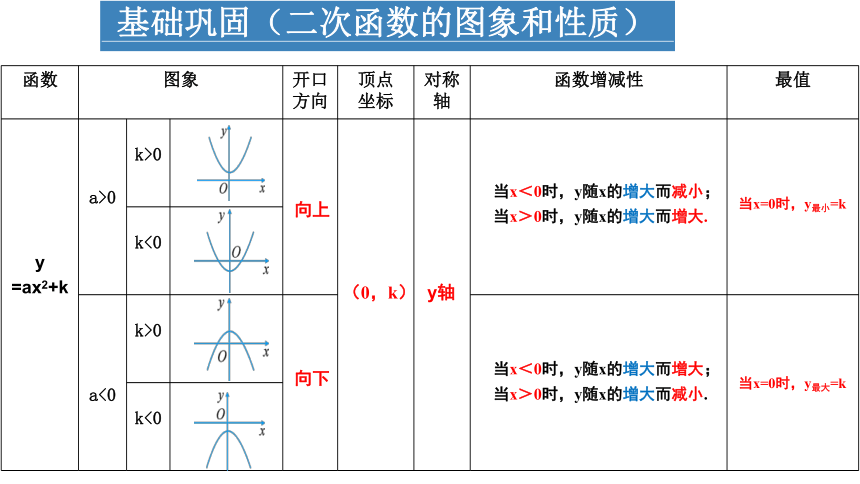
基础巩固(二次函数的图象和性质)
函数 图象 开口
方向 顶点
坐标 对称轴 函数增减性 最值
y =ax2+k
a>0
k>0
k<0
a<0
k>0
k<0
向上
向下
(0,k)
y轴
当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.
当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小.
当x=0时,y最小=k
当x=0时,y最大=k
基础巩固(二次函数的图象和性质)
方向
向上
向下
大小
越小
越大
顶点
y轴正半轴
坐标原点
y轴负半轴
向上
向下
|k|
基础巩固(二次函数的图象和性质)
基础巩固(二次函数的图象和性质)
向上
向下
(h,0)
x=h
当x<h时,y随x的增大而减小;当x>h时,y随x的增大而增大.
当x<h时,y随x的增大而增大;当x>h时,y随x的增大而减小.
当x=h时,y最小=0
当x=h时,y最大=0
基础巩固(二次函数的图象和性质)
方向
向上
向下
大小
越小
越大
对称轴
y轴右侧
y轴
y轴左侧
向右
向左
|h|
基础巩固(二次函数的图象和性质)
向上
向下
(h,k)
x=h
当x<h时,y随x的增大而减小;当x>h时,y随x的增大而增大.
当x<h时,y随x的增大而增大;当x>h时,y随x的增大而减小.
当x=h时,y最小=k
当x=h时,y最大=k
k﹥0
k﹤0
x
y
x
y
k﹥0
k﹤0
k﹥0
k﹤0
k﹥0
k﹤0
y
x
y
x
y
x
y
x
基础巩固(二次函数的图象和性质)
向上
向下
y
x
基础巩固(二次函数平移规律)
具体平移方法如下:
左右平移
上下平移 上下左右平移 上下平移
左右平移
基础巩固(二次函数的图象和性质)
3)交点式y=a(x-x1)(x-x2).当抛物线与x轴的两个交点为(x1,0)、(x2,0)时,可设y=a(x-x1)(x-x2),再将另一点的坐标代入即可求出a的值,从而写出二次函数的解析式.
求二次函数解析式的一般方法:
1)一般式y=ax2+bx+c.代入三个点的坐标列出关于a, b, c的方程组,并求出a, b, c,就可以写出二次函数的解析式.
2)顶点式y=a(x-h)2+k.根据顶坐标点(h,k),可设顶点式y=a(x-h)2+k,再将另一点的坐标代入,即可求出a的值,从而写出二次函数的解析式.
基础巩固(二次函数的图象和性质)
【问题】结合之前所学,你知道二次函数y=ax2+bx+c(a≠0)图象与二次项系数a的关系吗?
二次函数y=ax2+bx+c(a≠0)中
1)当a___0时,抛物线开口向_____,a的值越___,开口越____;
2)当a___0时,抛物线开口向_____,a的值越___,开口越____;
【总结】a的________决定开口方向,a的______决定开口的大小(|a|越______,抛物线的开口___).
y=2x2
y=x2
>
上
大
小
<
下
大
小
正负
大小
大
小
基础巩固(二次函数的图象和性质)
【问题】结合之前所学,你知道二次函数y=ax2+bx+c(a≠0)图象与一次项系数b的关系吗?
基础巩固(二次函数的图象和性质)
【问题】结合之前所学,你知道二次函数y=ax2+bx+c(a≠0)图象与常数项c的关系吗?
1)当c____0时,抛物线与y轴的交点在________;
2)当c____0时,抛物线与y轴的交点为________;
3)当c____0时,抛物线与y轴的交点在________。
【小结】c决定了抛物线与_______交点的位置.
>
y轴正半轴
坐标原点
y轴负半轴
=
<
y轴
基础巩固(二次函数与一元二次方程的关系)
二次函数y=ax2+bx+c的图象和x轴交点 一元二次方程ax2+bx+c= 0的根 一元二次方程ax2+bx+c= 0根的判别式Δ=b2-4ac
二次函数 y=ax2+bx+c 的图象和x轴交点的三种情况与一元二次方程根的关系:
2个交点
有两个不相等的实数根
1个交点
没有交点
有一个不相等的实数根
没有实数根
b2-4ac>0
b2-4ac=0
b2-4ac<0
基础巩固(二次函数与一元二次方程的关系)
二次函数
与一元二次方程
二次函数与一元二次方程的关系
有两个交点
根据二次函数图象
求一元二次方程的近似解
一个交点
无交点
有两个不相等的实数根
有两个相等的实数根
无实数根
基础巩固(二次函数与实际应用)
基础巩固(二次函数与实际应用)
1.分析题意,把实际问题转化为数学问题,画出图形.
2.根据已知条件建立适当的平面直角坐标系.
3.选用适当的函数解析式求解.
4.根据二次函数的解析式解决具体的实际问题.
抽象
转化
数学问题
运用
数学知识
解决问题
实际问题
[问题]简述利用二次函数解决实际问题的步骤?
基础巩固(二次函数与实际应用)
用二次函数解决实际问题的一般步骤:
1.审:仔细审题,理清题意;
2.设:找出题中的变量和常量,分析它们之间的关系,与图形相关的问题要结合图形具体分析,设出适当的未知数;
3.列:用二次函数表示出变量和常量之间的关系,建立二次函数模型,写出二次函数的解析式;
4.解:依据已知条件,借助二次函数的解析式、图象和性质等求解实际问题;
5.检:检验结果,进行合理取舍,得出符合实际意义的结论.
基础巩固(二次函数与实际应用)
[问题]简述利用二次函数解决面积最值的方法?
①找好自变量;
②利用相关的图象面积公式,列出函数关系式;
③利用函数的最值解决面积最值问题。
【注意】自变量的取决范围。
基础巩固(二次函数与实际应用)
[问题]简述利用二次函数解决利润最值的方法?
巧设未知数,根据利润公式列出函数关系式,再利用二次函数的最值解决利润最大问题是否存在最大利润问题。
基础巩固(二次函数与实际应用)
(1)建立适当的平面直角坐标系。
(2)根据题意找出已知点的坐标。
(3)求出抛物线解析式。
(4)直接利用图象解决实际问题。
[问题]简述利用二次函数解决拱桥问题的方法?
本章主要考查二次函数表达式、顶点坐标、开口方向、对称轴、最大(小)值、用二次函数模型解决生活实际问题。其中顶点坐标、开口方向、对称轴、最大(小)值、图象与坐标轴的交点等主要以填空题、选择题岀现。利用二次函数解决生活实际问题以及二次函数与几何知识相结合常以解答题形式出现。
题型一(二次函数的判断)
一次函数
不是整式方程
一次函数
二次函数
化简后为一次方程
【详解】解:二次函数y=3x-5x2+1的二次项系数、一次项系数、常数项分别为-5、3、1.
题型二(根据二次函数的定义求未知数的值)
1 已知y关于 x的函数y=(m2+2m)x2+mx+m+1.
1)当m为何值时,此函数是一次函数?
2)当m为何值时,此函数是二次函数?
【详解】
1)∵函数y=(m2+2m)x2+mx+m+1是一次函数,
∴m2+2m=0,m≠0,
解得:m=﹣2;
2)∵函数y=(m2+2m)x2+mx+m+1是二次函数,
∴m2+2m≠0,
解得:m≠﹣2且m≠0.
题型二(根据二次函数的定义求未知数的值)
根据二次函数的定义可得:m2﹣2m﹣1=2,且m2﹣m≠0,
解得,m=3或m=﹣1;
当m=3时,y=6x2+9;
当m=﹣1时,y=2x2﹣4x+1;
综上所述,该二次函数的解析式为:y=6x2+9或y=2x2﹣4x+1.
题型三(二次函数y=ax2的图象与性质)
y轴
(0,0)
②③⑤
①
①④
①②④
题型三(二次函数y=ax2的图象与性质)
题型三(二次函数y=ax2的图象与性质)
7.如图所示四个二次函数的图象中,分别对应的是①y=ax2;②y=bx2;③y=cx2;④y=dx2.则a、b、c、d的大小关系为_____.
8.如图,⊙O的半径为2,C1是函数y=2x2的图象,C2是函数y=-2x2的图象,则图中阴影部分的面积为_______.
a>b>d>c
2π
题型四(二次函数y=ax2 +k的图象与性质)
大
y=5
向上
y轴
(0,3)
题型四(二次函数y=ax2 +k的图象与性质)
题型四(二次函数y=ax2 +k的图象与性质)
题型五(二次函数y=a(x-h)2 的图象与性质)
(-3,0)
②
①
A
增大
题型五(二次函数y=a(x-h)2 的图象与性质)
【详解】解:y=a(x+m)2的对称轴为直线x=﹣m,
∵顶点在y轴的右侧,
∴﹣m>0,m<0,
∵am<0,
∴a>0,开口方向向上,
故答案为:向上.
6.已知二次函数y=(x-m)2,当x≤1时,y随x的增大而减小,则m的取值范围是__________.
7.已知抛物线y=a(x+m)2(m为常数)的顶点在y轴的右侧,且am<0,则此图象的开口方向 _____.
【详解】解:∵二次函数y=(x﹣m)2中,a=1>0,
∴此函数开口向上,
∵当x≤1时,函数值y随x的增大而减小,
∴二次函数的对称轴x=m≥1.故答案为:m≥1.
题型五(二次函数y=a(x-h)2 的图象与性质)
8.抛物线y=3(x-2)2与x轴交于点A,与y轴交于点B,求△AOB的面积和周长.
题型六(二次函数y=a(x-h)2 +k的图象与性质)
向上
x=2
(2,-3)
x=-3
-5
y=2(x+3)2+1
【详解】解:∵抛物线y=a(x+h)2-k的顶点坐标为(-h,-k),在第三象限,
∴-h<0,-k<0,
∴h>0,k>0.
故答案为:>,>.
-2
>
>
题型六(二次函数y=a(x-h)2 +k的图象与性质)
题型七(二次函数y=ax2+bx+c的图象与性质)
【详解】y=﹣x2+2mx=-( x2-2mx)=-( x2-2mx+m2)+m2=-( x-m)+m2,
∴顶点坐标为(m,m2),∴可能成为函数顶点的是(﹣2,4),故选A.
题型七(二次函数y=ax2+bx+c的图象与性质)
(3,5)
题型七(二次函数y=ax2+bx+c的图象与性质)
题型八(二次函数图象与各项系数符号)
1 二次函数y=ax2+bx+c(a≠0)的图象如图
1)a____0, b____0, c____0
2)2a+b ____0
3)4ac-b2____0
4)a+b+c____0
5)a-b+c____0
6)8a+c____0
7)当-1>
<
<
1
=
<
<
=
>
<
题型八(二次函数图象与各项系数符号)
题型八(二次函数图象与各项系数符号)
题型九(待定系数法求二次函数解析式)
1(2020·江苏常州市·九年级期末)二次函数y=ax2+bx+c的y与x的部分对应值如下表:
则下列判断中正确的是( )
A.抛物线开口向上 B.抛物线与y轴交于负半轴
C.当x=﹣1时y>0 D.方程ax2+bx+c=0的负根在0与﹣1之间
题型十(二次函数与一元二次方程)
题型十(二次函数与一元二次方程)
题型十一(利用二次函数解决实际问题)
1 如图,某中学课外活动小组准备围建一个矩形苗圃园.其中一边靠墙,另外三边用长为20米的篱笆围成.已知墙长为18米,设这个苗圃园垂直于墙的一边的长为x米.
(1)若这个苗圃园的面积为S平方米,求出S与x之间的函数关系式,并写出自变量x的取值范围;
(2)垂直于墙的一边的长为多少米时,这个苗圃园的面积最大,并求出这个最大面积.
题型十一(利用二次函数解决实际问题)
2 如图1,是抛物线形的拱桥,当拱顶高水面2米时,水面宽4米.如图建立平面直角坐标系,解答下列问题:
(1)如图2,求该抛物线的函数解析式.
(2)当水面AB下降1米,到CD处时,水面宽度增加多少米?(保留根号)
(3)当水面AB上升1米时,水面宽度减少多少米?(保留根号)
题型十一(利用二次函数解决实际问题)
3 某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,那么销售单价应控制在什么范围内?
【详解】解:(1)y=(x﹣50)[50+5(100﹣x)]=﹣5x2+800x﹣27500,
∴y=﹣5x2+800x﹣27500(50≤x≤100);
(2)y=﹣5x2+800x﹣27500=﹣5(x﹣80)2+4500,∵a=﹣5<0,∴抛物线开口向下.
∵50≤x≤100,对称轴是直线x=80,∴当x=80时,y最大值=4500;
(3)当y=4000时,﹣5(x﹣80)2+4500=4000,解得x1=70,x2=90.
∴当70≤x≤90时,每天的销售利润不低于4000元.
题型十一(利用二次函数解决实际问题)
4 如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?
二次函数在初中数学中占有重要地位,在中考命题中一直是“重头戏”,根据历年中考试卷的分析,历年中考中对二次函数的考查题型有低档的填空题、选择题,中高档的解答题,除考查定义、识图、性质、求解析式等常规题外,还会出现与二次函数有关的贴近生活实际的应用题,阅读理解题和探究题,二次函数与其他函数程、不等式、几何知识的综合在压轴题中出现的可能性很大。二次函数与几何综合作为中考压轴题,常考查函数解析式、交点坐标、图形面积或周长、存在性问题、图形的平移、对称、旋转等,其综合性强,难度大, 是“数”与“形”的相互结合,相互渗透。
2022年中考真题
2022年中考真题
2022年中考真题
2022年中考真题
2022年中考真题
2022年中考真题
2022年中考真题
2022年中考真题
2023年中考真题
2023年中考真题
学习目标
1 掌握二次函数的概念,并能根据二次函数的图像与性质解决相关问题。
2 掌握用待定系数法求抛物线解析式的方法。
3 能够利用二次函数解决有关实际问题,能根据具体问题的实际意义检验结果的合理性,进一步培养学生分析问题、解决问题的意识和能力。
本章重点内容:
1 掌握二次函数的图象特征及其性质;
2 掌握用待定系数法求抛物线解析式的方法。
本章难点内容:
1 理解二次函数与一元二次方程的关系;
2 利用二次函数解决实际问题。
二次函数是初中阶段函数中的重要函数,它在解决各类数学问题和实际问题中有着广泛的应用。掌握二次函数图象和性质是学习二次函数的基础,根据二次函数图象判断抛物线抛的开口方向,顶点坐标,对称轴,与坐标轴交点坐标、确定二次函数的解析式为必须掌握内容,理解二次函数与各系数之间的关系,灵活运用二次函数解决实际问题。二次函数是体现综合性的重点内容,在期中期末试卷中即有相对稳定的基础题,也有新颖的试题来考查学生的分析,解决问题能力,实践和创新能力,因此经常与一次函数,三角形,四边形知识结合在一起,成为试卷的压轴题。
基础巩固(二次函数的定义)
一般地,形如y=ax +bx+c(其中a、b、c是常数,a≠0)的函数叫做二次函数。其中,x是自变量,a、b、c分别是函数解析式的二次项系数、一次项系数和常数项。
【提问】同学们,谈谈你对二次函数的理解,需要注意些什么?
1)含有一个自变量,且自变量的最高次数为2。
2)二次项系数不等于0。
3)等式两边都是整式。
4)一般情况下,自变量x的取值范围是任意实数。
基础巩固(二次函数的定义)
二次函数的特殊形式:
基础巩固(二次函数的定义)
基础巩固(二次函数的图象和性质)
向上
向下
(0,0)
y轴
当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.
当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小.
当x=0时,y最小=0
当x=0时,y最大=0
方向
向上
向下
大小
越小
越大
基础巩固(二次函数的图象和性质)
二次函数y=ax2 中比较函数值的大小的方法:
方法 步骤 适用范围
直接代入法 将x的值分别代入到函数解析式中,
求出y值再比较大小 多用于a值确定
性质判断法 结合二次函数的性质(增减性)及自变量x之间的大小关系,得出其对应y值的大小关系 多用于自变量x在对称轴同一侧的情况
草图法 画出二次函数的草图并描点,
根据图象直接判断y值的大小 多用于a值不确定且x值不在对称轴同侧的情况
基础巩固(二次函数的图象和性质)
基础巩固(二次函数的图象和性质)
函数 图象 开口
方向 顶点
坐标 对称轴 函数增减性 最值
y =ax2+k
a>0
k>0
k<0
a<0
k>0
k<0
向上
向下
(0,k)
y轴
当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.
当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小.
当x=0时,y最小=k
当x=0时,y最大=k
基础巩固(二次函数的图象和性质)
方向
向上
向下
大小
越小
越大
顶点
y轴正半轴
坐标原点
y轴负半轴
向上
向下
|k|
基础巩固(二次函数的图象和性质)
基础巩固(二次函数的图象和性质)
向上
向下
(h,0)
x=h
当x<h时,y随x的增大而减小;当x>h时,y随x的增大而增大.
当x<h时,y随x的增大而增大;当x>h时,y随x的增大而减小.
当x=h时,y最小=0
当x=h时,y最大=0
基础巩固(二次函数的图象和性质)
方向
向上
向下
大小
越小
越大
对称轴
y轴右侧
y轴
y轴左侧
向右
向左
|h|
基础巩固(二次函数的图象和性质)
向上
向下
(h,k)
x=h
当x<h时,y随x的增大而减小;当x>h时,y随x的增大而增大.
当x<h时,y随x的增大而增大;当x>h时,y随x的增大而减小.
当x=h时,y最小=k
当x=h时,y最大=k
k﹥0
k﹤0
x
y
x
y
k﹥0
k﹤0
k﹥0
k﹤0
k﹥0
k﹤0
y
x
y
x
y
x
y
x
基础巩固(二次函数的图象和性质)
向上
向下
y
x
基础巩固(二次函数平移规律)
具体平移方法如下:
左右平移
上下平移 上下左右平移 上下平移
左右平移
基础巩固(二次函数的图象和性质)
3)交点式y=a(x-x1)(x-x2).当抛物线与x轴的两个交点为(x1,0)、(x2,0)时,可设y=a(x-x1)(x-x2),再将另一点的坐标代入即可求出a的值,从而写出二次函数的解析式.
求二次函数解析式的一般方法:
1)一般式y=ax2+bx+c.代入三个点的坐标列出关于a, b, c的方程组,并求出a, b, c,就可以写出二次函数的解析式.
2)顶点式y=a(x-h)2+k.根据顶坐标点(h,k),可设顶点式y=a(x-h)2+k,再将另一点的坐标代入,即可求出a的值,从而写出二次函数的解析式.
基础巩固(二次函数的图象和性质)
【问题】结合之前所学,你知道二次函数y=ax2+bx+c(a≠0)图象与二次项系数a的关系吗?
二次函数y=ax2+bx+c(a≠0)中
1)当a___0时,抛物线开口向_____,a的值越___,开口越____;
2)当a___0时,抛物线开口向_____,a的值越___,开口越____;
【总结】a的________决定开口方向,a的______决定开口的大小(|a|越______,抛物线的开口___).
y=2x2
y=x2
>
上
大
小
<
下
大
小
正负
大小
大
小
基础巩固(二次函数的图象和性质)
【问题】结合之前所学,你知道二次函数y=ax2+bx+c(a≠0)图象与一次项系数b的关系吗?
基础巩固(二次函数的图象和性质)
【问题】结合之前所学,你知道二次函数y=ax2+bx+c(a≠0)图象与常数项c的关系吗?
1)当c____0时,抛物线与y轴的交点在________;
2)当c____0时,抛物线与y轴的交点为________;
3)当c____0时,抛物线与y轴的交点在________。
【小结】c决定了抛物线与_______交点的位置.
>
y轴正半轴
坐标原点
y轴负半轴
=
<
y轴
基础巩固(二次函数与一元二次方程的关系)
二次函数y=ax2+bx+c的图象和x轴交点 一元二次方程ax2+bx+c= 0的根 一元二次方程ax2+bx+c= 0根的判别式Δ=b2-4ac
二次函数 y=ax2+bx+c 的图象和x轴交点的三种情况与一元二次方程根的关系:
2个交点
有两个不相等的实数根
1个交点
没有交点
有一个不相等的实数根
没有实数根
b2-4ac>0
b2-4ac=0
b2-4ac<0
基础巩固(二次函数与一元二次方程的关系)
二次函数
与一元二次方程
二次函数与一元二次方程的关系
有两个交点
根据二次函数图象
求一元二次方程的近似解
一个交点
无交点
有两个不相等的实数根
有两个相等的实数根
无实数根
基础巩固(二次函数与实际应用)
基础巩固(二次函数与实际应用)
1.分析题意,把实际问题转化为数学问题,画出图形.
2.根据已知条件建立适当的平面直角坐标系.
3.选用适当的函数解析式求解.
4.根据二次函数的解析式解决具体的实际问题.
抽象
转化
数学问题
运用
数学知识
解决问题
实际问题
[问题]简述利用二次函数解决实际问题的步骤?
基础巩固(二次函数与实际应用)
用二次函数解决实际问题的一般步骤:
1.审:仔细审题,理清题意;
2.设:找出题中的变量和常量,分析它们之间的关系,与图形相关的问题要结合图形具体分析,设出适当的未知数;
3.列:用二次函数表示出变量和常量之间的关系,建立二次函数模型,写出二次函数的解析式;
4.解:依据已知条件,借助二次函数的解析式、图象和性质等求解实际问题;
5.检:检验结果,进行合理取舍,得出符合实际意义的结论.
基础巩固(二次函数与实际应用)
[问题]简述利用二次函数解决面积最值的方法?
①找好自变量;
②利用相关的图象面积公式,列出函数关系式;
③利用函数的最值解决面积最值问题。
【注意】自变量的取决范围。
基础巩固(二次函数与实际应用)
[问题]简述利用二次函数解决利润最值的方法?
巧设未知数,根据利润公式列出函数关系式,再利用二次函数的最值解决利润最大问题是否存在最大利润问题。
基础巩固(二次函数与实际应用)
(1)建立适当的平面直角坐标系。
(2)根据题意找出已知点的坐标。
(3)求出抛物线解析式。
(4)直接利用图象解决实际问题。
[问题]简述利用二次函数解决拱桥问题的方法?
本章主要考查二次函数表达式、顶点坐标、开口方向、对称轴、最大(小)值、用二次函数模型解决生活实际问题。其中顶点坐标、开口方向、对称轴、最大(小)值、图象与坐标轴的交点等主要以填空题、选择题岀现。利用二次函数解决生活实际问题以及二次函数与几何知识相结合常以解答题形式出现。
题型一(二次函数的判断)
一次函数
不是整式方程
一次函数
二次函数
化简后为一次方程
【详解】解:二次函数y=3x-5x2+1的二次项系数、一次项系数、常数项分别为-5、3、1.
题型二(根据二次函数的定义求未知数的值)
1 已知y关于 x的函数y=(m2+2m)x2+mx+m+1.
1)当m为何值时,此函数是一次函数?
2)当m为何值时,此函数是二次函数?
【详解】
1)∵函数y=(m2+2m)x2+mx+m+1是一次函数,
∴m2+2m=0,m≠0,
解得:m=﹣2;
2)∵函数y=(m2+2m)x2+mx+m+1是二次函数,
∴m2+2m≠0,
解得:m≠﹣2且m≠0.
题型二(根据二次函数的定义求未知数的值)
根据二次函数的定义可得:m2﹣2m﹣1=2,且m2﹣m≠0,
解得,m=3或m=﹣1;
当m=3时,y=6x2+9;
当m=﹣1时,y=2x2﹣4x+1;
综上所述,该二次函数的解析式为:y=6x2+9或y=2x2﹣4x+1.
题型三(二次函数y=ax2的图象与性质)
y轴
(0,0)
②③⑤
①
①④
①②④
题型三(二次函数y=ax2的图象与性质)
题型三(二次函数y=ax2的图象与性质)
7.如图所示四个二次函数的图象中,分别对应的是①y=ax2;②y=bx2;③y=cx2;④y=dx2.则a、b、c、d的大小关系为_____.
8.如图,⊙O的半径为2,C1是函数y=2x2的图象,C2是函数y=-2x2的图象,则图中阴影部分的面积为_______.
a>b>d>c
2π
题型四(二次函数y=ax2 +k的图象与性质)
大
y=5
向上
y轴
(0,3)
题型四(二次函数y=ax2 +k的图象与性质)
题型四(二次函数y=ax2 +k的图象与性质)
题型五(二次函数y=a(x-h)2 的图象与性质)
(-3,0)
②
①
A
增大
题型五(二次函数y=a(x-h)2 的图象与性质)
【详解】解:y=a(x+m)2的对称轴为直线x=﹣m,
∵顶点在y轴的右侧,
∴﹣m>0,m<0,
∵am<0,
∴a>0,开口方向向上,
故答案为:向上.
6.已知二次函数y=(x-m)2,当x≤1时,y随x的增大而减小,则m的取值范围是__________.
7.已知抛物线y=a(x+m)2(m为常数)的顶点在y轴的右侧,且am<0,则此图象的开口方向 _____.
【详解】解:∵二次函数y=(x﹣m)2中,a=1>0,
∴此函数开口向上,
∵当x≤1时,函数值y随x的增大而减小,
∴二次函数的对称轴x=m≥1.故答案为:m≥1.
题型五(二次函数y=a(x-h)2 的图象与性质)
8.抛物线y=3(x-2)2与x轴交于点A,与y轴交于点B,求△AOB的面积和周长.
题型六(二次函数y=a(x-h)2 +k的图象与性质)
向上
x=2
(2,-3)
x=-3
-5
y=2(x+3)2+1
【详解】解:∵抛物线y=a(x+h)2-k的顶点坐标为(-h,-k),在第三象限,
∴-h<0,-k<0,
∴h>0,k>0.
故答案为:>,>.
-2
>
>
题型六(二次函数y=a(x-h)2 +k的图象与性质)
题型七(二次函数y=ax2+bx+c的图象与性质)
【详解】y=﹣x2+2mx=-( x2-2mx)=-( x2-2mx+m2)+m2=-( x-m)+m2,
∴顶点坐标为(m,m2),∴可能成为函数顶点的是(﹣2,4),故选A.
题型七(二次函数y=ax2+bx+c的图象与性质)
(3,5)
题型七(二次函数y=ax2+bx+c的图象与性质)
题型八(二次函数图象与各项系数符号)
1 二次函数y=ax2+bx+c(a≠0)的图象如图
1)a____0, b____0, c____0
2)2a+b ____0
3)4ac-b2____0
4)a+b+c____0
5)a-b+c____0
6)8a+c____0
7)当-1
<
<
1
=
<
<
=
>
<
题型八(二次函数图象与各项系数符号)
题型八(二次函数图象与各项系数符号)
题型九(待定系数法求二次函数解析式)
1(2020·江苏常州市·九年级期末)二次函数y=ax2+bx+c的y与x的部分对应值如下表:
则下列判断中正确的是( )
A.抛物线开口向上 B.抛物线与y轴交于负半轴
C.当x=﹣1时y>0 D.方程ax2+bx+c=0的负根在0与﹣1之间
题型十(二次函数与一元二次方程)
题型十(二次函数与一元二次方程)
题型十一(利用二次函数解决实际问题)
1 如图,某中学课外活动小组准备围建一个矩形苗圃园.其中一边靠墙,另外三边用长为20米的篱笆围成.已知墙长为18米,设这个苗圃园垂直于墙的一边的长为x米.
(1)若这个苗圃园的面积为S平方米,求出S与x之间的函数关系式,并写出自变量x的取值范围;
(2)垂直于墙的一边的长为多少米时,这个苗圃园的面积最大,并求出这个最大面积.
题型十一(利用二次函数解决实际问题)
2 如图1,是抛物线形的拱桥,当拱顶高水面2米时,水面宽4米.如图建立平面直角坐标系,解答下列问题:
(1)如图2,求该抛物线的函数解析式.
(2)当水面AB下降1米,到CD处时,水面宽度增加多少米?(保留根号)
(3)当水面AB上升1米时,水面宽度减少多少米?(保留根号)
题型十一(利用二次函数解决实际问题)
3 某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,那么销售单价应控制在什么范围内?
【详解】解:(1)y=(x﹣50)[50+5(100﹣x)]=﹣5x2+800x﹣27500,
∴y=﹣5x2+800x﹣27500(50≤x≤100);
(2)y=﹣5x2+800x﹣27500=﹣5(x﹣80)2+4500,∵a=﹣5<0,∴抛物线开口向下.
∵50≤x≤100,对称轴是直线x=80,∴当x=80时,y最大值=4500;
(3)当y=4000时,﹣5(x﹣80)2+4500=4000,解得x1=70,x2=90.
∴当70≤x≤90时,每天的销售利润不低于4000元.
题型十一(利用二次函数解决实际问题)
4 如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?
二次函数在初中数学中占有重要地位,在中考命题中一直是“重头戏”,根据历年中考试卷的分析,历年中考中对二次函数的考查题型有低档的填空题、选择题,中高档的解答题,除考查定义、识图、性质、求解析式等常规题外,还会出现与二次函数有关的贴近生活实际的应用题,阅读理解题和探究题,二次函数与其他函数程、不等式、几何知识的综合在压轴题中出现的可能性很大。二次函数与几何综合作为中考压轴题,常考查函数解析式、交点坐标、图形面积或周长、存在性问题、图形的平移、对称、旋转等,其综合性强,难度大, 是“数”与“形”的相互结合,相互渗透。
2022年中考真题
2022年中考真题
2022年中考真题
2022年中考真题
2022年中考真题
2022年中考真题
2022年中考真题
2022年中考真题
2023年中考真题
2023年中考真题
同课章节目录
