数学人教A版(2019)选择性必修第一册3.2.1双曲线及其标准方程 课件(共15张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册3.2.1双曲线及其标准方程 课件(共15张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 674.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-05 07:35:17 | ||
图片预览




文档简介
(共15张PPT)
3.2.1 双曲线及其标准方程
问题2:椭圆的定义是什么?
问题1:椭圆的标准方程是怎样的 及a,b,c的关系。
复习引入复习引入
探究:平面内到两个定点F1、F2的距离的差
等于非零常数的动点的轨迹又是什么呢?
探究:平面内到两个定点F1、F2的距离的差
等于非零常数的动点的轨迹又是什么呢?
①如图(A),
|MF1|-|MF2|=2a(2a是常数)
②如图(B),
|MF2|-|MF1|=2a(2a是常数)
上面两条曲线合起来叫做双曲线,
其中每一条叫做双曲线的一支
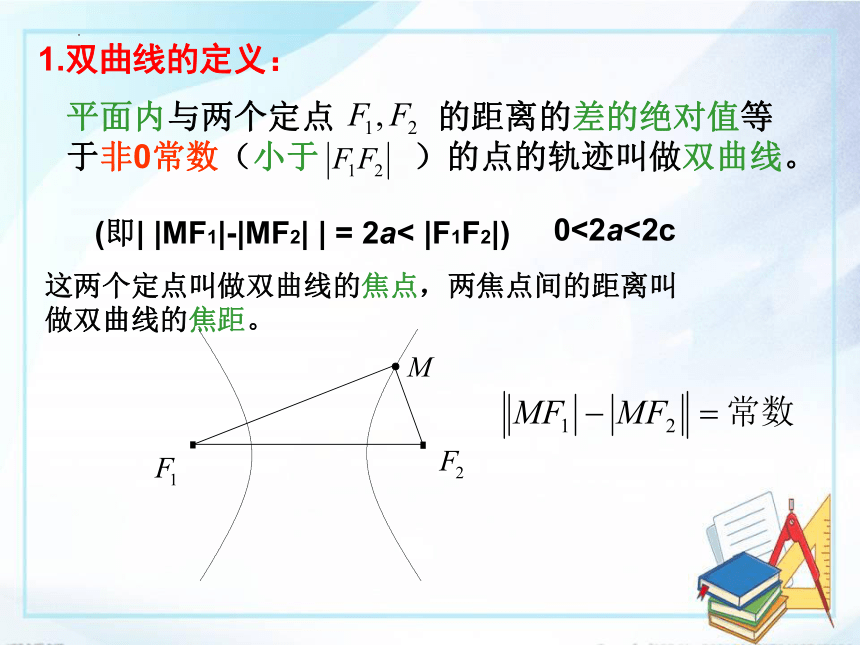
1.双曲线的定义:
平面内与两个定点 的距离的差的绝对值等于非0常数(小于 )的点的轨迹叫做双曲线。
这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距。
(即| |MF1|-|MF2| | = 2a< |F1F2|)
0<2a<2c
F
2
F
1
M
x
O
y
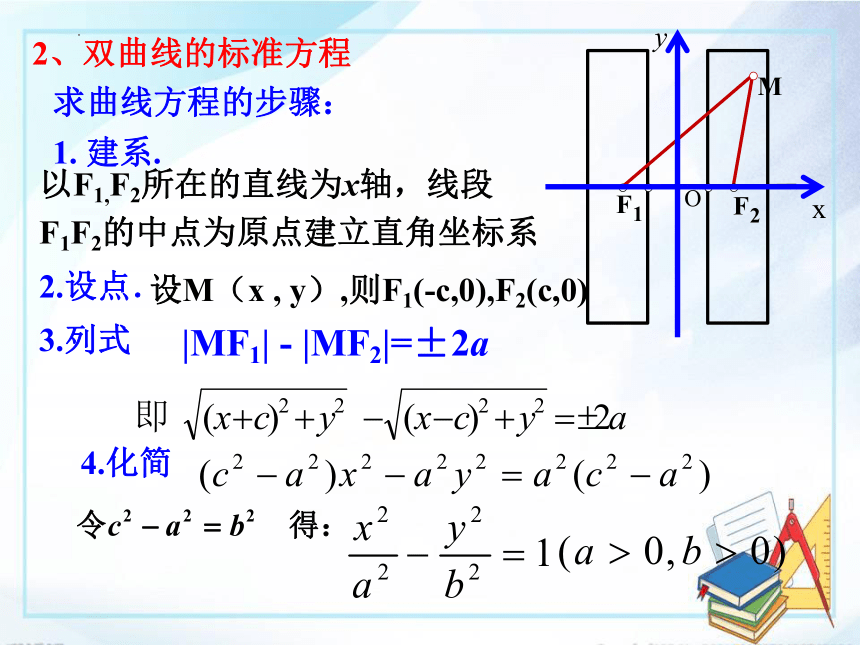
求曲线方程的步骤:
2、双曲线的标准方程
1. 建系.
以F1,F2所在的直线为x轴,线段
F1F2的中点为原点建立直角坐标系
2.设点.
设M(x , y),则F1(-c,0),F2(c,0)
3.列式
|MF1| - |MF2|=±2a
4.化简
F
2
F
1
M
x
O
y
O
M
F2
F1
x
y
焦点在x轴上
焦点在y轴上
标准方程为:
思考:如何
从双曲线的标准方程中看出焦点的位置?
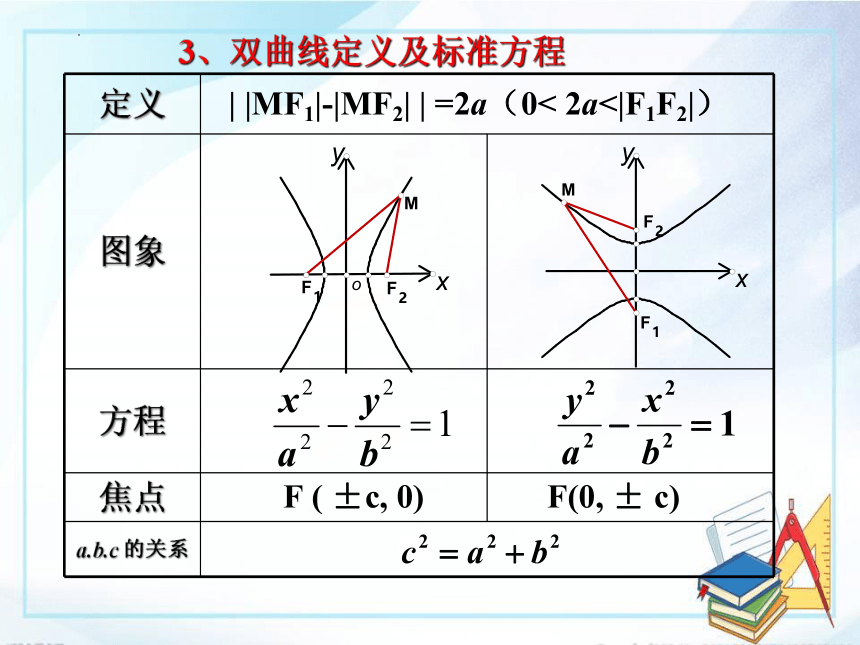
定义 图象
方程
焦点
a.b.c 的关系 | |MF1|-|MF2| | =2a(0< 2a<|F1F2|)
F ( ±c, 0)
3、双曲线定义及标准方程
F(0, ± c)
练习练习
1、判断下列方程是否表示双曲线?若是,求
出 及焦点坐标。
椭圆 双曲线
4、双曲线与椭圆之间的区别与联系
例1、已知双曲线的两个焦点为F1(-5,0),F2(5,0),
双曲线上一点P到F1、F2的距离的差的绝对值等于6,
求双曲线的标准方程.
解:依题意可设双曲线的标准方程为
∵2a=6,2c=10 ∴a=3,c=5,
∴该双曲线的标准方程为
故b2=25-9=16
例1、已知双曲线的两个焦点为F1(-5,0),F2(5,0),
双曲线上一点P到F1、F2的距离的差的绝对值等于6,
求双曲线的标准方程.
变式1:若|PF1|=10,求|PF2|?
变式2:若|PF1|-|PF2|=6,则点P的轨迹是什么?
4或16
双曲线的右支
变式3:若P到F1、F2距离的差的绝对值等于10呢?
变式4:若P到F1、F2距离的差的绝对值等于0呢?
两条射线
F1F2的垂直平分线
2、 已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程。
解:建立直角坐标系xOy,使A,B两点在x轴上,并且坐标原点O与线段AB的中点重合
设爆炸点P的坐标为(x,y),则
︱PA︱-︱PB︱=340×2=680
即2a=680,a=340
又︱AB︱=800,所以2c=800,c=400
b =c -a =44400
因为︱PA︱-︱PB︱=340×2=680>0,所以x>0
因此炮弹爆炸点的轨迹(双曲线)的方程为
P
x
y
O
A
B
练习练习
小结:小结:
1、双曲线的定义及理解
2、双曲线的标准方程及应用
3.2.1 双曲线及其标准方程
问题2:椭圆的定义是什么?
问题1:椭圆的标准方程是怎样的 及a,b,c的关系。
复习引入复习引入
探究:平面内到两个定点F1、F2的距离的差
等于非零常数的动点的轨迹又是什么呢?
探究:平面内到两个定点F1、F2的距离的差
等于非零常数的动点的轨迹又是什么呢?
①如图(A),
|MF1|-|MF2|=2a(2a是常数)
②如图(B),
|MF2|-|MF1|=2a(2a是常数)
上面两条曲线合起来叫做双曲线,
其中每一条叫做双曲线的一支
1.双曲线的定义:
平面内与两个定点 的距离的差的绝对值等于非0常数(小于 )的点的轨迹叫做双曲线。
这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距。
(即| |MF1|-|MF2| | = 2a< |F1F2|)
0<2a<2c
F
2
F
1
M
x
O
y
求曲线方程的步骤:
2、双曲线的标准方程
1. 建系.
以F1,F2所在的直线为x轴,线段
F1F2的中点为原点建立直角坐标系
2.设点.
设M(x , y),则F1(-c,0),F2(c,0)
3.列式
|MF1| - |MF2|=±2a
4.化简
F
2
F
1
M
x
O
y
O
M
F2
F1
x
y
焦点在x轴上
焦点在y轴上
标准方程为:
思考:如何
从双曲线的标准方程中看出焦点的位置?
定义 图象
方程
焦点
a.b.c 的关系 | |MF1|-|MF2| | =2a(0< 2a<|F1F2|)
F ( ±c, 0)
3、双曲线定义及标准方程
F(0, ± c)
练习练习
1、判断下列方程是否表示双曲线?若是,求
出 及焦点坐标。
椭圆 双曲线
4、双曲线与椭圆之间的区别与联系
例1、已知双曲线的两个焦点为F1(-5,0),F2(5,0),
双曲线上一点P到F1、F2的距离的差的绝对值等于6,
求双曲线的标准方程.
解:依题意可设双曲线的标准方程为
∵2a=6,2c=10 ∴a=3,c=5,
∴该双曲线的标准方程为
故b2=25-9=16
例1、已知双曲线的两个焦点为F1(-5,0),F2(5,0),
双曲线上一点P到F1、F2的距离的差的绝对值等于6,
求双曲线的标准方程.
变式1:若|PF1|=10,求|PF2|?
变式2:若|PF1|-|PF2|=6,则点P的轨迹是什么?
4或16
双曲线的右支
变式3:若P到F1、F2距离的差的绝对值等于10呢?
变式4:若P到F1、F2距离的差的绝对值等于0呢?
两条射线
F1F2的垂直平分线
2、 已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程。
解:建立直角坐标系xOy,使A,B两点在x轴上,并且坐标原点O与线段AB的中点重合
设爆炸点P的坐标为(x,y),则
︱PA︱-︱PB︱=340×2=680
即2a=680,a=340
又︱AB︱=800,所以2c=800,c=400
b =c -a =44400
因为︱PA︱-︱PB︱=340×2=680>0,所以x>0
因此炮弹爆炸点的轨迹(双曲线)的方程为
P
x
y
O
A
B
练习练习
小结:小结:
1、双曲线的定义及理解
2、双曲线的标准方程及应用
