21.5 反比例函数 同步练习 (含解析)2022-2023学年上学期安徽省九年级数学期末试题选编
文档属性
| 名称 | 21.5 反比例函数 同步练习 (含解析)2022-2023学年上学期安徽省九年级数学期末试题选编 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-05 22:05:20 | ||
图片预览




文档简介
21.5 反比例函数
一、单选题
1.(2022秋·安徽安庆·九年级统考期末)下列各点中,在反比例函数图象上点的坐标是( )
A. B. C. D.
2.(2022秋·安徽合肥·九年级统考期末)下列函数中,是反比例函数的是( )
A.y=x B.y=-2x+3 C.y=- D.y=-
3.(2022秋·安徽宿州·九年级统考期末)如果反比例函数的图象经过点,则( )
A.18 B. C.16 D.
4.(2022秋·安徽亳州·九年级统考期末)已知双曲线经过点,则它还经过的点是( )
A. B. C. D.
5.(2022秋·安徽滁州·九年级统考期末)反比例函数经过点,则下列说法错误的是( )
A. B.函数图象分布在第一、三象限
C.当时,随的增大而增大 D.当时,随的增大而减小
6.(2022秋·安徽宣城·九年级统考期末)反比例函数图像经过的点是( )
A. B. C. D.
7.(2022秋·安徽芜湖·九年级统考期末)反比例函数经过经过下面哪一个点( )
A. B. C. D.
8.(2022秋·安徽宿州·九年级统考期末)关于反比例函数的图象,下列说法中, 错误的是( )
A.点(1,-1)在它的图象上 B.图象位于第二 、四象限
C.图象的两个分支关于原点对称 D.x的值越大,图象越接近x轴
9.(2022秋·安徽阜阳·九年级统考期末)如图所示的是反比例函数与二次函数的图象,则k与a的值可能为( ).
A. B. C. D.
10.(2022秋·安徽蚌埠·九年级统考期末)若双曲线的图象的一支位于第三象限,则k的取值范围是( )
A. B. C. D.
11.(2022秋·安徽合肥·九年级统考期末)已知点(a,m),(b,n)在反比例函数的图像上,若a<b<0,则下列说法正确的是( )
A.m<n B.m=n C.m>n D.m,n的大小无法确定
12.(2022秋·安徽淮南·九年级统考期末)若,则下列函数:①,②,③中,y的值随x的值增大而增大的函数共有( )
A.0个 B.1个 C.2个 D.3个
13.(2022秋·安徽安庆·九年级统考期末)反比例函数图象的每条曲线上y都随x增大而减小,则k的取值范围是( )
A. B. C. D.
14.(2022秋·安徽六安·九年级统考期末)若反比例函数在每个象限内,随的增大而减小,则( )
A. B. C. D.
15.(2022秋·安徽铜陵·九年级统考期末)已知点A(-3,a)、B (1,b)、C(4,c)在函数的图象上,则a、b、c的大小关系是( )
A.c >a > b B.b >a > c C.a> b > c D.b>c>a
16.(2022秋·安徽芜湖·九年级统考期末)已知点,,均在反比例函数的图象上,且,则下列各式正确的是( )
A. B. C. D.
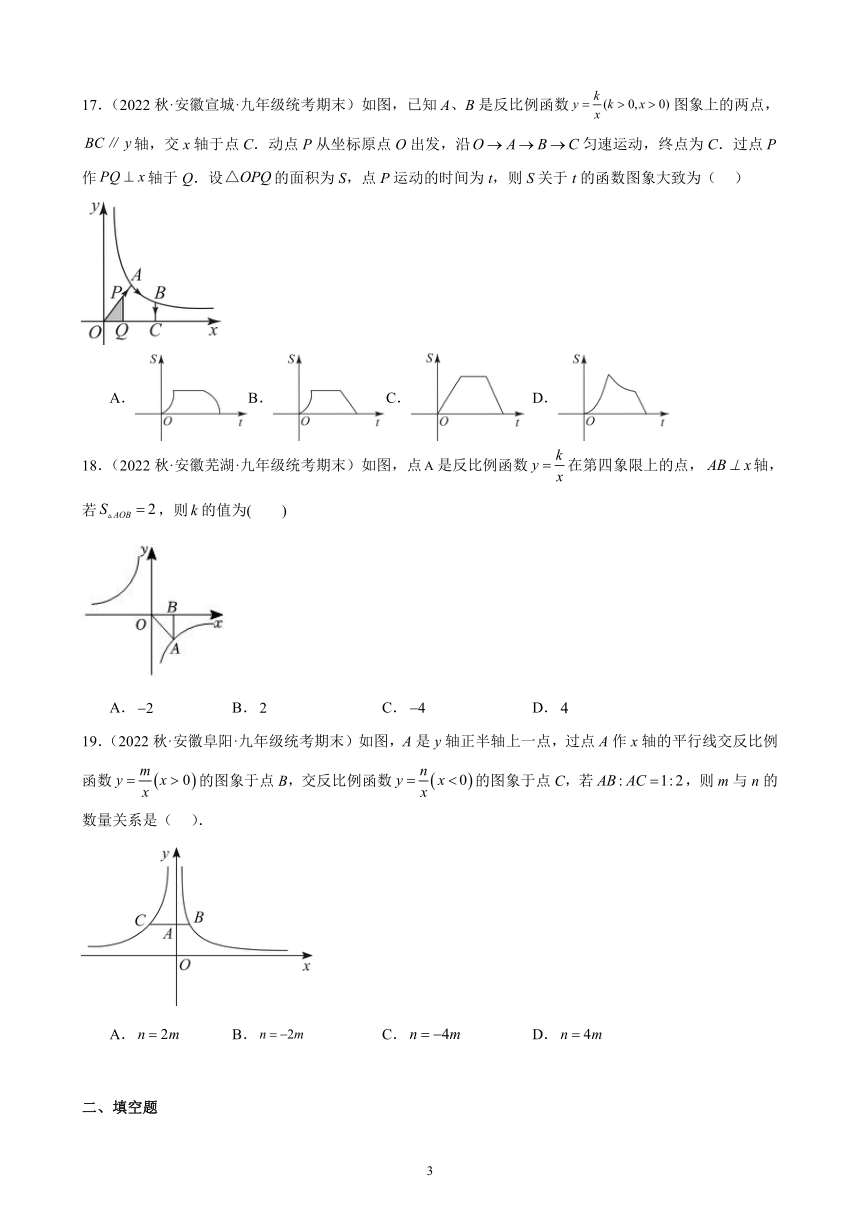
17.(2022秋·安徽宣城·九年级统考期末)如图,已知A、B是反比例函数图象上的两点,轴,交x轴于点C.动点P从坐标原点O出发,沿匀速运动,终点为C.过点P作轴于Q.设的面积为S,点P运动的时间为t,则S关于t的函数图象大致为( )
A.B.C. D.
18.(2022秋·安徽芜湖·九年级统考期末)如图,点是反比例函数在第四象限上的点,轴,若,则的值为( )
A. B. C. D.
19.(2022秋·安徽阜阳·九年级统考期末)如图,A是y轴正半轴上一点,过点A作x轴的平行线交反比例函数的图象于点B,交反比例函数的图象于点C,若,则m与n的数量关系是( ).
A. B. C. D.
二、填空题
20.(2022秋·安徽六安·九年级统考期末)已知反比例函数的图像经过点,则的值是 .
21.(2022秋·安徽宣城·九年级统考期末)反比例函数的图象的一个分支在第二象限,则m的取值范围是 .
22.(2022秋·安徽宿州·九年级统考期末)如图,过y轴上任意一点p,作x轴的平行线,分别与反比例函数和的图象交于A点和B点.若C为x轴上任意一点,连接,则的面积为 .
23.(2022秋·安徽阜阳·九年级统考期末)如图,平面直角坐标系中,A是y轴正半轴上一点,且,,P是线段的三等分点(靠近点A),反比例函数的图象经过点P,且与相交于点Q.
(1)点P的坐标为 .(用含k的代数式表示)
(2)若的面积为,则k的值为 .
三、解答题
24.(2022秋·安徽亳州·九年级统考期末)已知点在双曲线上.
(1)求a的值;
(2)当时,求y的取值范围.
25.(2022秋·安徽安庆·九年级统考期末)如图,直线与双曲线交于A,B两点,其中.
(1)求点B的坐标;
(2)求的面积;
(3)直接写出不等式的解集.
26.(2022秋·安徽·九年级统考期末)冉冉录入一篇文章,录入时间(分钟)与录字速度(字/分钟)之间的关系如图所示;
(1)求与间的函数表达式;
(2)若冉冉将原有录入速度提高,结果提前2分钟完成了录入任务,求冉冉原来的录入速度.
27.(2022秋·安徽六安·九年级统考期末)东东在网上销售一种成本为30元/件的T恤衫.销售过程中的其他各种费用(不再含T恤衫成本)总计50(百元).若销售价格为x(元/件).销售量为y(百件).当时,y与x之间满足一次函数关系.且当时,,有关销售量y(百件)与销售价格x(元/件)的相关信息如下:
销售量y(百件) _____________
销售价格x(元/件)
(1)求当时.y与x的函数关系式:
(2)①求销售这种T恤衫的纯利润w(百元)与销售价格x(元/件)的函数关系式;
②销售价格定为每件多少元时.获得的利润最大 最大利润是多少
28.(2022秋·安徽蚌埠·九年级统考期末)如图,直线与双曲线相交于A,B两点,与x轴交于点C,若点A,B的横坐标分别是1和2,
(1)请直接写出的解集;
(2)当的面积为3时,求的值.
29.(2022秋·安徽合肥·九年级统考期末)如图,一次函数的图象与反比例函数的图象交于点、,交轴于点,交轴于点.
(1)求反比例函数和一次函数的表达式;
(2)连接、,求的面积;
(3)直接写出时的取值范围.
30.(2022秋·安徽宣城·九年级统考期末)如图,已知反比例函数和一次函数的图像交于点两点.
(1)求m、n的值;
(2)连接,求的面积.
31.(2022秋·安徽·九年级统考期末)如图,反比例函数的图象经过格点(网格线的交点),过点作轴于点.
(1)求反比例函数的表达式.
(2)已知直线经过格点,交轴于点.记(不含边界)围成的区域为.当直线经过格点时,区域内的格点坐标有几个?分别为哪些?
参考答案:
1.A
【分析】根据反比例函数图象上点的坐标特征进行判断.
【详解】解:∵1×2=2,-2×1=-2,2×=1,×2=1,
∴点在反比例函数图象上的点.
故选:A.
【点睛】本题考查了反比例函数图象上点的坐标特征:反比例函数(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.
2.C
【分析】根据反比例函数的定义判断即可.
【详解】解:A.y=x是正比例函数,故此选项不符合题意;
B.y=-2x+3是一次函数,故此选项不符合题意;
C.y=-是反比例函数,故此选项符合题意;
D.y=-不是反比例函数,故此选项不符合题意;
故选:C.
【点睛】本题考查了反比例函数的定义,熟练掌握反比例函数的定义是解题的关键.
3.D
【分析】直接把点代入反比例函数的解析式,即可求出k的值.
【详解】解:∵反比例函数的图象经过点,
∴,
∴;
故选:D.
【点睛】本题考核反比例函数的解析式,解题的关键是运用反比例函数的性质求参数.
4.D
【分析】设双曲线的解析式为,根据题意求得,进而根据,逐项分析判断即可.
【详解】设双曲线的解析式为,双曲线经过点,
A. ,,故该选项不正确,不符合题意;
B. ,,故该选项不正确,不符合题意;
C. ,,故该选项不正确,不符合题意;
D. ,,故该选项正确,符合题意.
故选D.
【点睛】本题考查了反比例函数的代数意义,求得的值是解题的关键.
5.C
【分析】将点(2,1)代入中求出k值,再根据反比例函数的性质对四个选项逐一分析即可.
【详解】将点(2,1)代入中,解得:k=2,
A.k=2,此说法正确,不符合题意;
B.k=2﹥0,反比例函数图象分布在第一、三象限,此书说法正确,不符合题意;
C.k=2﹥0且x﹥0,函数图象位于第一象限,且y随x的增大而减小,此说法错误,符合题意;
D.k=2﹥0且x﹥0,函数图象位于第一象限,且y随x的增大而减小,此说法正确,不符合题意;
故选:C.
【点睛】本题考查了反比例函数的性质,熟练掌握反比例函数的性质,理解函数图象上的点与解析式的关系是解答的关键.
6.D
【分析】根据反比例函数的性质,对选项逐个判断即可.
【详解】解:A、当时,,过点,不符合题意;
B、当时,,过点,不符合题意;
C、当时,,过点,不符合题意;
D、当时,,过点,符合题意;
故选:D
【点睛】此题考查了反比例函数的性质,解题的关键是熟练掌握反比例函数的有关性质.
7.B
【分析】将横坐标分别代入函数解析式求出纵坐标,进一步比较即可.
【详解】解:当时,,
故A选项不符合题意;
当时,,
故B选项符合题意;
当时,,
故C选项不符合题意;
当时,,
故D选项不符合题意;
故选:B.
【点睛】本题考查了反比例函数图象上点的坐标特征,熟练掌握反比例函数图象上点的坐标特征是解题的关键.
8.D
【分析】利用的图象与性质逐一分析每个选项,即可得到答案.
【详解】解:当时, 故不符合题意;
<
的图像位于第二 、四象限,故不符合题意;
的图象的两个分支关于原点成中心对称,故不符合题意;
的图象在第四象限内的值越大,图象越接近轴,故符合题意;
故选:
【点睛】本题考查的是反比例函数的图象与性质,掌握以上知识是解题的关键.
9.B
【分析】根据图象判断出的符号,再进行判读即可.
【详解】解:由图象可知:双曲线过二,四象限,抛物线开口向下,
∴,
只有B选项符合题意;
故选B.
【点睛】本题考查反比例函数的图象,以及二次函数的图象与系数的关系.熟练掌握反比例函数和二次函数的图象和性质,是解题的关键.
10.A
【分析】反比例函数的图象是双曲线,当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小.
【详解】解:∵双曲线的图象的一支位于第三象限,
∴1﹣k>0,
∴;
故选:A.
【点睛】此题考查了反比例函数的图象与性质,反比例函数y(k≠0),当k>0时,图象在第一、三象限,且在每一个象限y随x的增大而减小;当k<0时,函数图象在第二、四象限,且在每一个象限y随x的增大而增大,熟练掌握反比例函数的性质是解本题的关键.
11.A
【分析】根据a、b与0的大小关系利用反比例函数的性质确定答案即可.
【详解】解:∵反比例函数y=﹣中k=﹣3<0,
∴在每一象限内y随着x的增大而增大,
∵点(a,m),(b,n)在反比例函数y=﹣的图象上,且a<b<0,,
∴m<n
故选:A.
【点睛】本题考查反比例函数的性质,掌握反比例函数的图象特点是解题关键.
12.C
【分析】①根据反比例函数的性质判断即可;
②∵m<0,∴﹣m>0,根据一次函数性质判断即可;
③根据二次函数的性质进行分析即可.
【详解】解:①∵m<0,∴x>0时,y的值随x的值增大而增大,符合题意;
②∵m<﹣0,∴﹣m>0,∴y的值随x的值增大而增大,符合题意;
③∵m<0∴开口向下,时,y的值随x的值增大而减小,不符合题意;
故选:C.
【点睛】本题考查的是一次函数、反比例函数和二次函数的性质,掌握一次函数、反比例函数和二次函数的增减性是解题的关键.
13.C
【分析】根据反比例函数的图象和性质解题即可.
【详解】∵反比例函数图象的每条曲线上y都随x增大而减小,
∴,
解得:.
故选C.
【点睛】本题考查反比例函数的图象和性质.掌握反比例函数,当时,图象位于第一、三象限,且y随x的增大而减小;当时,图象位于第二、四象限,且y随x的增大而增大是解题关键.
14.A
【分析】根据反比例函数的性质,当时,在每个象限内随的增大而减小;当时,在每个象限内随的增大而增大.
【详解】∵反比例函数在每个象限内,随的增大而减小,
∴,
∴.
故选:A.
【点睛】本题主要考查反比例函数的性质,解决此题的关键是熟练掌握反比例函数中的正负对函数增减性的影响.
15.D
【分析】根据,即可知反比例函数其比例系数k>0,再结合反比例函数的图象和性质即可解答.
【详解】∵,
∴反比例函数的图象在第一、三象限,
∴当x>0时,y>0,且y随x的增大而减小,
当x<0时,y<0,且y随x的增大而减小.
∵
∴.
故选D.
【点睛】本题考查平方的非负性和反比例函数的图象和性质.求出反比例函数其比例系数k>0是解题关键.
16.C
【分析】先根据反比例函数中判断出函数图象所在的象限及增减性,再根据各点横坐标的特点即可得出结论.
【详解】∵反比例函数中,,
∴函数图象分别位于一、三象限,且在每一象限内y随x的增大而减小,
∵,
∴点位于第一象限,且,
∵
∴位于第三象限,且,
∴.
故选:C.
【点睛】本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.
17.B
【分析】分别判断当点P在线段上运动时,当点P在上运动时,点P在上运动时的图像变化趋势,即可作出选择.
【详解】解:当点P在线段上运动时,设直线的表达式为,
点P的坐标满足,则(a是大于0的常数,),图象为抛物线的一部分;
当点P在上运动时,此时的面积(),保持不变;
点P在上运动时,设路线的总路程为l,点P的速度为b,则,因为l,,b均是常数,所以S与t成一次函数关系.
综上所述,S关于t的函数图象大致为B选项,
故选:B.
【点睛】本题考查了函数综合和动点问题的函数图象,解题的关键是根据点的移动确定函数的种类,从而确定其图象.
18.C
【分析】根据反比例函数系数的几何意义可知,以及当时反比例函数在二、四象限,可求值.
【详解】解:由反比例函数系数的几何意义可知,
,
反比例函数图形在第二、四象限,
,
.
故选:C.
【点睛】本题考查反比例函数系数的几何意义,解题关键是熟知反比例函数系数的几何意义以及反比例函数图象位置与的关系.
19.B
【分析】首先根据轴,,可设,,根据在反比例函数的图象上,可得,再根据C在反比例函数的图象上,可得,即可得答案.
【详解】解:∵轴,
设,
∵
∴,
在反比例函数的图象上,
,
∵C在反比例函数的图象上,
∴,
∴,
∴,
故先:B.
【点睛】此题主要考查了反比例函数图象上点的坐标特点,反比例函数图象上的点的横纵坐标的积是定值,即.
20.﹣12
【分析】直接将点代入反比例函数解析式中,解之即可.
【详解】依题意,将点代入,得:,
解得:=﹣12,
故答案为:﹣12.
【点睛】本题主要考查反比例函数图象上的点的坐标特征,熟练掌握图象上的坐标与解析式的关系是解答的关键.
21./
【分析】根据反比例函数的图象的一个分支在第二象限,可得,解不等式即可求解.
【详解】解:反比例函数的图象的一个分支在第二象限,
,
解得,
故答案为:.
【点睛】本题考查了反比例函数的图象与性质,熟练掌握和运用反比例函数的图象与性质是解决本题的关键.
22.3
【分析】先设,由直线轴,则,两点的纵坐标都为,而,分别在反比例函数和的图象上,可得到点坐标为,,点坐标为,,从而求出的长,然后根据三角形的面积公式计算即可.
【详解】解:设,
直线轴,
,两点的纵坐标都为,而点在反比例函数的图象上,
当,,即点坐标为,,
又点在反比例函数的图象上,
当,,即点坐标为,,
,
.
故答案为:3.
【点睛】本题考查的是反比例函数系数的几何意义,即在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是,且保持不变.
23. 6
【分析】(1)利用P是线段的三等分点(靠近点A),得到,根据得到,设点的横坐标为(),则,表示出,利用反比例函数的图象经过点P,即可求得,求得点的坐标;
(2)由(1)知,,求得点的坐标为,判断出直线的解析式为,由题意得,得到,最后利用的面积为,列出方程即可求解.
【详解】解:(1)∵P是线段的三等分点(靠近点A),
∴,
∵,
∴,
∵,
设点的横坐标为(),则,
∴纵坐标为,
∴,
∵反比例函数的图象经过点P,
∴,解得,
∴,
故答案为:
(2)由(1)知,,
∵,
∴点的坐标为,
则直线的解析式为,
由题意得,解得或,
∵点在第一象限,
∴,
∵的面积为,
∴,
解得,
故答案为:6
【点睛】本题考查了反比例函数的图象和性质,理解掌握反比例函数图象上点的坐标特征是解题的关键.
24.(1)
(2)
【分析】(1)将点代入解析式即可求解,
(2)根据反比例函数图象的性质求解即可.
【详解】(1)解:将点代入解析式得,
解得
(2)当时,
当时,
当时,的图象,随的增大而减小,
【点睛】本题考查了反比例函数的定义以及反比例函数图像的性质,掌握反比例函数的图象的性质是解题的关键.
25.(1)
(2)6
(3)或
【分析】(1)先利用待定系数法求得两函数的解析式,再联立方程组求解点B坐标即可;
(2)先求得直线与y轴的交点C的坐标得到,再由求解即可;
(3)根据图像直接求解即可.
【详解】(1)解:把代入,得:,解得:,
∴;
把代入,得:,解得:,
∴;
联立,解得:或,
∴.
(2)解:设与y轴交于点C,当时,,
∴,则,
∴.
(3)解:当或时,,
∴不等式的解集为或.
【点睛】本题考查反比例函数与一次函数的交点问题,涉及待定系数法函数解函数解析式、坐标与图形、解二元一次方程组、图像法解不等式的解集等知识,理解题意,利用数形结合思想求解是解答的关键.
26.(1)
(2)125字/分钟
【分析】(1)根据录入的时间录入总量录入速度即可得出函数关系式;
(2)设冉冉实际用了t分钟,则原计划用时分钟,由题意得关于t的分式方程,解方程即可求出t的值.
【详解】(1)解:设
把代入 得,
,
∴y与x的函数表达式为 ;
(2)设冉冉实际用了t分钟,则原计划用时分钟,原来的录入速度为x字/分钟
由题意得, ,
整理得: ,
∵录入速度提高了,则实际录入速度为字/分,
则 即 ,
解得:,
经检验是原方程的解,
冉冉原录入速度为:(字/分钟),
答:冉冉原来的录入速度为125字/分钟.
【点睛】本题考查了反比例函数的应用、解分式方程,根据工作量得到等量关系是解决本题的关键.
27.(1)
(2)①当时,;当时,;
②销售价格定为80元/件时,获得的利润最大,最大利润是100百元
【分析】(1)把把代入得,设y与x的函数关系式为:y=kx+b,把x=40,y=6;x=60,y=4,代入解方程组即可得到结论;
(2)①根据x的范围分类讨论,由“总利润=单件利润×销售量”可得函数解析式;
②结合①中两个函数解析式,分别依据二次函数的性质和反比例函数的性质求其最值即可.
【详解】(1)解:把代入得.
设y与x的函数关系式为:,
∵当时,,当时,,
∴,
解得:,
∴y与x的函数关系式为:.
(2)①当时,;
当时,;
②当时,,
∵随x的增大而增大.
∴当 (百元).
当时,
∵,
∴w随x的增大而增大,当时, (百元).
答:销售价格定为80元/件时,获得的利润最大,最大利润是100百元.
【点睛】本题主要考查二次函数和反比例函数的应用,理解题意依据相等关系列出函数解析式,并熟练掌握二次函数和反比例函数的性质是解题的关键.
28.(1)1<x<2
(2)4
【分析】(1)根据图象即可求得;
(2)设A(1,k2),B(2,),由S△AOB=S△AOM+S梯形AMNB﹣S△BON=S梯形AMNB得到关于k2的方程,解方程即可.
【详解】(1)直线y=k1x+b与双曲线y(x>0)交于A,B两点,且点A,B的横坐标分别是1和2,
由图象可知:不等式k1x+b的解集是1<x<2;
(2)作AM⊥x轴于M,BN⊥x轴于N,则S△AOM=S△BON|k2|,
设A(1,k2),B(2,),
∵△AOB的面积为3,
∴S△AOB=S△AOM+S梯形AMNB﹣S△BON=S梯形AMNB(k2)×(2﹣1)=3,
∴k2=4.
∴k2的值为4.
【点睛】本题是反比例函数与一次函数的交点问题,考查了反比例函数图象上点的坐标特征以及三角形面积等,数形结合是解题的关键.
29.(1)反比例函数解析式为,一次函数解析式为;(2)10.5;(3)或
【分析】(1)把的坐标代入反比例函数的解析式求出,把的坐标代入反比例函数解析式求出,把,的坐标代入一次函数的解析式得出方程组,求出方程组的解即可;
(2)求出一次函数与x轴的交点坐标,得到的值,根据三角形的面积公式求出即可;
(3)结合图象和,的坐标即可求出答案.
【详解】解:(1)∵把A(-2,-5)代入代入得:,
∴,
∴反比例函数解析式为,
∵把C(5,n)代入得反比例函数中得:,
∴C点的坐标为(5,2),
∵把A、C的坐标代入得:,
∴
∴一次函数解析式为;
(2)把y=0代入得:x=3,
∴D点坐标为(3,0),
∴OD=3,
∴;
(3)根据函数图像可知,当时,即一次函数图像在反比例函数图像的下方时自变量的取值范围,
∴当时,或.
【点睛】本题考查了反比例函数和一次函数解析式的确定、图形的面积求法及函数图象与不等式等知识点,正确求得函数解析式是解决问题的关键,解决本题注意利用数形结合思想.
30.(1),
(2)
【分析】(1)先将点A的坐标代入反比例函数的解析式,求出m的值,再把点B的坐标代入反比例函数的解析式,即可求出n的值;
(2)作轴于点C,轴于点D,根据、进行求解即可.
【详解】(1)把带入得:,
∴,
把带入得:;
(2)作轴于点C,轴于点D,
则,
∵,
∴.
【点睛】本题考查了待定系数法求反比例函数的解析式,求反比例函数图象上点的坐标,比例系数k的几何意义,反比例函数与图形的面积,熟练掌握知识点是解题的关键.
31.(1)
(2)区域内的格点坐标有3个,分别为,,.
【分析】(1)将点代入反比例函数即可求解;
(2)当直线经过格点,点,求出直线的解析式,结合图象即可求得内的格点坐标及个数;
【详解】(1)将点代入反比例函数,得:
,
∴,
∴反比例函数的表达式为:;
(2)∵直线经过格点,点,
∴,
解得:,
∴直线的解析式为,
如图所示:
∵点,轴于点,
∴点,
故区域的左边界为线段的部分,其解析式为:,
上方的边界为线段的部分,其解析式为,
令,得:,
∴点坐标为:,
故当时,,即与,
当时,,即,
∴区域内的格点坐标有3个,分别为,,.
【点睛】本题考查一次函数与反比例函数的图象及性质,熟练掌握待定系数法求解析式是解题的关键是,学会利用数形结合的思想.
一、单选题
1.(2022秋·安徽安庆·九年级统考期末)下列各点中,在反比例函数图象上点的坐标是( )
A. B. C. D.
2.(2022秋·安徽合肥·九年级统考期末)下列函数中,是反比例函数的是( )
A.y=x B.y=-2x+3 C.y=- D.y=-
3.(2022秋·安徽宿州·九年级统考期末)如果反比例函数的图象经过点,则( )
A.18 B. C.16 D.
4.(2022秋·安徽亳州·九年级统考期末)已知双曲线经过点,则它还经过的点是( )
A. B. C. D.
5.(2022秋·安徽滁州·九年级统考期末)反比例函数经过点,则下列说法错误的是( )
A. B.函数图象分布在第一、三象限
C.当时,随的增大而增大 D.当时,随的增大而减小
6.(2022秋·安徽宣城·九年级统考期末)反比例函数图像经过的点是( )
A. B. C. D.
7.(2022秋·安徽芜湖·九年级统考期末)反比例函数经过经过下面哪一个点( )
A. B. C. D.
8.(2022秋·安徽宿州·九年级统考期末)关于反比例函数的图象,下列说法中, 错误的是( )
A.点(1,-1)在它的图象上 B.图象位于第二 、四象限
C.图象的两个分支关于原点对称 D.x的值越大,图象越接近x轴
9.(2022秋·安徽阜阳·九年级统考期末)如图所示的是反比例函数与二次函数的图象,则k与a的值可能为( ).
A. B. C. D.
10.(2022秋·安徽蚌埠·九年级统考期末)若双曲线的图象的一支位于第三象限,则k的取值范围是( )
A. B. C. D.
11.(2022秋·安徽合肥·九年级统考期末)已知点(a,m),(b,n)在反比例函数的图像上,若a<b<0,则下列说法正确的是( )
A.m<n B.m=n C.m>n D.m,n的大小无法确定
12.(2022秋·安徽淮南·九年级统考期末)若,则下列函数:①,②,③中,y的值随x的值增大而增大的函数共有( )
A.0个 B.1个 C.2个 D.3个
13.(2022秋·安徽安庆·九年级统考期末)反比例函数图象的每条曲线上y都随x增大而减小,则k的取值范围是( )
A. B. C. D.
14.(2022秋·安徽六安·九年级统考期末)若反比例函数在每个象限内,随的增大而减小,则( )
A. B. C. D.
15.(2022秋·安徽铜陵·九年级统考期末)已知点A(-3,a)、B (1,b)、C(4,c)在函数的图象上,则a、b、c的大小关系是( )
A.c >a > b B.b >a > c C.a> b > c D.b>c>a
16.(2022秋·安徽芜湖·九年级统考期末)已知点,,均在反比例函数的图象上,且,则下列各式正确的是( )
A. B. C. D.
17.(2022秋·安徽宣城·九年级统考期末)如图,已知A、B是反比例函数图象上的两点,轴,交x轴于点C.动点P从坐标原点O出发,沿匀速运动,终点为C.过点P作轴于Q.设的面积为S,点P运动的时间为t,则S关于t的函数图象大致为( )
A.B.C. D.
18.(2022秋·安徽芜湖·九年级统考期末)如图,点是反比例函数在第四象限上的点,轴,若,则的值为( )
A. B. C. D.
19.(2022秋·安徽阜阳·九年级统考期末)如图,A是y轴正半轴上一点,过点A作x轴的平行线交反比例函数的图象于点B,交反比例函数的图象于点C,若,则m与n的数量关系是( ).
A. B. C. D.
二、填空题
20.(2022秋·安徽六安·九年级统考期末)已知反比例函数的图像经过点,则的值是 .
21.(2022秋·安徽宣城·九年级统考期末)反比例函数的图象的一个分支在第二象限,则m的取值范围是 .
22.(2022秋·安徽宿州·九年级统考期末)如图,过y轴上任意一点p,作x轴的平行线,分别与反比例函数和的图象交于A点和B点.若C为x轴上任意一点,连接,则的面积为 .
23.(2022秋·安徽阜阳·九年级统考期末)如图,平面直角坐标系中,A是y轴正半轴上一点,且,,P是线段的三等分点(靠近点A),反比例函数的图象经过点P,且与相交于点Q.
(1)点P的坐标为 .(用含k的代数式表示)
(2)若的面积为,则k的值为 .
三、解答题
24.(2022秋·安徽亳州·九年级统考期末)已知点在双曲线上.
(1)求a的值;
(2)当时,求y的取值范围.
25.(2022秋·安徽安庆·九年级统考期末)如图,直线与双曲线交于A,B两点,其中.
(1)求点B的坐标;
(2)求的面积;
(3)直接写出不等式的解集.
26.(2022秋·安徽·九年级统考期末)冉冉录入一篇文章,录入时间(分钟)与录字速度(字/分钟)之间的关系如图所示;
(1)求与间的函数表达式;
(2)若冉冉将原有录入速度提高,结果提前2分钟完成了录入任务,求冉冉原来的录入速度.
27.(2022秋·安徽六安·九年级统考期末)东东在网上销售一种成本为30元/件的T恤衫.销售过程中的其他各种费用(不再含T恤衫成本)总计50(百元).若销售价格为x(元/件).销售量为y(百件).当时,y与x之间满足一次函数关系.且当时,,有关销售量y(百件)与销售价格x(元/件)的相关信息如下:
销售量y(百件) _____________
销售价格x(元/件)
(1)求当时.y与x的函数关系式:
(2)①求销售这种T恤衫的纯利润w(百元)与销售价格x(元/件)的函数关系式;
②销售价格定为每件多少元时.获得的利润最大 最大利润是多少
28.(2022秋·安徽蚌埠·九年级统考期末)如图,直线与双曲线相交于A,B两点,与x轴交于点C,若点A,B的横坐标分别是1和2,
(1)请直接写出的解集;
(2)当的面积为3时,求的值.
29.(2022秋·安徽合肥·九年级统考期末)如图,一次函数的图象与反比例函数的图象交于点、,交轴于点,交轴于点.
(1)求反比例函数和一次函数的表达式;
(2)连接、,求的面积;
(3)直接写出时的取值范围.
30.(2022秋·安徽宣城·九年级统考期末)如图,已知反比例函数和一次函数的图像交于点两点.
(1)求m、n的值;
(2)连接,求的面积.
31.(2022秋·安徽·九年级统考期末)如图,反比例函数的图象经过格点(网格线的交点),过点作轴于点.
(1)求反比例函数的表达式.
(2)已知直线经过格点,交轴于点.记(不含边界)围成的区域为.当直线经过格点时,区域内的格点坐标有几个?分别为哪些?
参考答案:
1.A
【分析】根据反比例函数图象上点的坐标特征进行判断.
【详解】解:∵1×2=2,-2×1=-2,2×=1,×2=1,
∴点在反比例函数图象上的点.
故选:A.
【点睛】本题考查了反比例函数图象上点的坐标特征:反比例函数(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.
2.C
【分析】根据反比例函数的定义判断即可.
【详解】解:A.y=x是正比例函数,故此选项不符合题意;
B.y=-2x+3是一次函数,故此选项不符合题意;
C.y=-是反比例函数,故此选项符合题意;
D.y=-不是反比例函数,故此选项不符合题意;
故选:C.
【点睛】本题考查了反比例函数的定义,熟练掌握反比例函数的定义是解题的关键.
3.D
【分析】直接把点代入反比例函数的解析式,即可求出k的值.
【详解】解:∵反比例函数的图象经过点,
∴,
∴;
故选:D.
【点睛】本题考核反比例函数的解析式,解题的关键是运用反比例函数的性质求参数.
4.D
【分析】设双曲线的解析式为,根据题意求得,进而根据,逐项分析判断即可.
【详解】设双曲线的解析式为,双曲线经过点,
A. ,,故该选项不正确,不符合题意;
B. ,,故该选项不正确,不符合题意;
C. ,,故该选项不正确,不符合题意;
D. ,,故该选项正确,符合题意.
故选D.
【点睛】本题考查了反比例函数的代数意义,求得的值是解题的关键.
5.C
【分析】将点(2,1)代入中求出k值,再根据反比例函数的性质对四个选项逐一分析即可.
【详解】将点(2,1)代入中,解得:k=2,
A.k=2,此说法正确,不符合题意;
B.k=2﹥0,反比例函数图象分布在第一、三象限,此书说法正确,不符合题意;
C.k=2﹥0且x﹥0,函数图象位于第一象限,且y随x的增大而减小,此说法错误,符合题意;
D.k=2﹥0且x﹥0,函数图象位于第一象限,且y随x的增大而减小,此说法正确,不符合题意;
故选:C.
【点睛】本题考查了反比例函数的性质,熟练掌握反比例函数的性质,理解函数图象上的点与解析式的关系是解答的关键.
6.D
【分析】根据反比例函数的性质,对选项逐个判断即可.
【详解】解:A、当时,,过点,不符合题意;
B、当时,,过点,不符合题意;
C、当时,,过点,不符合题意;
D、当时,,过点,符合题意;
故选:D
【点睛】此题考查了反比例函数的性质,解题的关键是熟练掌握反比例函数的有关性质.
7.B
【分析】将横坐标分别代入函数解析式求出纵坐标,进一步比较即可.
【详解】解:当时,,
故A选项不符合题意;
当时,,
故B选项符合题意;
当时,,
故C选项不符合题意;
当时,,
故D选项不符合题意;
故选:B.
【点睛】本题考查了反比例函数图象上点的坐标特征,熟练掌握反比例函数图象上点的坐标特征是解题的关键.
8.D
【分析】利用的图象与性质逐一分析每个选项,即可得到答案.
【详解】解:当时, 故不符合题意;
<
的图像位于第二 、四象限,故不符合题意;
的图象的两个分支关于原点成中心对称,故不符合题意;
的图象在第四象限内的值越大,图象越接近轴,故符合题意;
故选:
【点睛】本题考查的是反比例函数的图象与性质,掌握以上知识是解题的关键.
9.B
【分析】根据图象判断出的符号,再进行判读即可.
【详解】解:由图象可知:双曲线过二,四象限,抛物线开口向下,
∴,
只有B选项符合题意;
故选B.
【点睛】本题考查反比例函数的图象,以及二次函数的图象与系数的关系.熟练掌握反比例函数和二次函数的图象和性质,是解题的关键.
10.A
【分析】反比例函数的图象是双曲线,当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小.
【详解】解:∵双曲线的图象的一支位于第三象限,
∴1﹣k>0,
∴;
故选:A.
【点睛】此题考查了反比例函数的图象与性质,反比例函数y(k≠0),当k>0时,图象在第一、三象限,且在每一个象限y随x的增大而减小;当k<0时,函数图象在第二、四象限,且在每一个象限y随x的增大而增大,熟练掌握反比例函数的性质是解本题的关键.
11.A
【分析】根据a、b与0的大小关系利用反比例函数的性质确定答案即可.
【详解】解:∵反比例函数y=﹣中k=﹣3<0,
∴在每一象限内y随着x的增大而增大,
∵点(a,m),(b,n)在反比例函数y=﹣的图象上,且a<b<0,,
∴m<n
故选:A.
【点睛】本题考查反比例函数的性质,掌握反比例函数的图象特点是解题关键.
12.C
【分析】①根据反比例函数的性质判断即可;
②∵m<0,∴﹣m>0,根据一次函数性质判断即可;
③根据二次函数的性质进行分析即可.
【详解】解:①∵m<0,∴x>0时,y的值随x的值增大而增大,符合题意;
②∵m<﹣0,∴﹣m>0,∴y的值随x的值增大而增大,符合题意;
③∵m<0∴开口向下,时,y的值随x的值增大而减小,不符合题意;
故选:C.
【点睛】本题考查的是一次函数、反比例函数和二次函数的性质,掌握一次函数、反比例函数和二次函数的增减性是解题的关键.
13.C
【分析】根据反比例函数的图象和性质解题即可.
【详解】∵反比例函数图象的每条曲线上y都随x增大而减小,
∴,
解得:.
故选C.
【点睛】本题考查反比例函数的图象和性质.掌握反比例函数,当时,图象位于第一、三象限,且y随x的增大而减小;当时,图象位于第二、四象限,且y随x的增大而增大是解题关键.
14.A
【分析】根据反比例函数的性质,当时,在每个象限内随的增大而减小;当时,在每个象限内随的增大而增大.
【详解】∵反比例函数在每个象限内,随的增大而减小,
∴,
∴.
故选:A.
【点睛】本题主要考查反比例函数的性质,解决此题的关键是熟练掌握反比例函数中的正负对函数增减性的影响.
15.D
【分析】根据,即可知反比例函数其比例系数k>0,再结合反比例函数的图象和性质即可解答.
【详解】∵,
∴反比例函数的图象在第一、三象限,
∴当x>0时,y>0,且y随x的增大而减小,
当x<0时,y<0,且y随x的增大而减小.
∵
∴.
故选D.
【点睛】本题考查平方的非负性和反比例函数的图象和性质.求出反比例函数其比例系数k>0是解题关键.
16.C
【分析】先根据反比例函数中判断出函数图象所在的象限及增减性,再根据各点横坐标的特点即可得出结论.
【详解】∵反比例函数中,,
∴函数图象分别位于一、三象限,且在每一象限内y随x的增大而减小,
∵,
∴点位于第一象限,且,
∵
∴位于第三象限,且,
∴.
故选:C.
【点睛】本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.
17.B
【分析】分别判断当点P在线段上运动时,当点P在上运动时,点P在上运动时的图像变化趋势,即可作出选择.
【详解】解:当点P在线段上运动时,设直线的表达式为,
点P的坐标满足,则(a是大于0的常数,),图象为抛物线的一部分;
当点P在上运动时,此时的面积(),保持不变;
点P在上运动时,设路线的总路程为l,点P的速度为b,则,因为l,,b均是常数,所以S与t成一次函数关系.
综上所述,S关于t的函数图象大致为B选项,
故选:B.
【点睛】本题考查了函数综合和动点问题的函数图象,解题的关键是根据点的移动确定函数的种类,从而确定其图象.
18.C
【分析】根据反比例函数系数的几何意义可知,以及当时反比例函数在二、四象限,可求值.
【详解】解:由反比例函数系数的几何意义可知,
,
反比例函数图形在第二、四象限,
,
.
故选:C.
【点睛】本题考查反比例函数系数的几何意义,解题关键是熟知反比例函数系数的几何意义以及反比例函数图象位置与的关系.
19.B
【分析】首先根据轴,,可设,,根据在反比例函数的图象上,可得,再根据C在反比例函数的图象上,可得,即可得答案.
【详解】解:∵轴,
设,
∵
∴,
在反比例函数的图象上,
,
∵C在反比例函数的图象上,
∴,
∴,
∴,
故先:B.
【点睛】此题主要考查了反比例函数图象上点的坐标特点,反比例函数图象上的点的横纵坐标的积是定值,即.
20.﹣12
【分析】直接将点代入反比例函数解析式中,解之即可.
【详解】依题意,将点代入,得:,
解得:=﹣12,
故答案为:﹣12.
【点睛】本题主要考查反比例函数图象上的点的坐标特征,熟练掌握图象上的坐标与解析式的关系是解答的关键.
21./
【分析】根据反比例函数的图象的一个分支在第二象限,可得,解不等式即可求解.
【详解】解:反比例函数的图象的一个分支在第二象限,
,
解得,
故答案为:.
【点睛】本题考查了反比例函数的图象与性质,熟练掌握和运用反比例函数的图象与性质是解决本题的关键.
22.3
【分析】先设,由直线轴,则,两点的纵坐标都为,而,分别在反比例函数和的图象上,可得到点坐标为,,点坐标为,,从而求出的长,然后根据三角形的面积公式计算即可.
【详解】解:设,
直线轴,
,两点的纵坐标都为,而点在反比例函数的图象上,
当,,即点坐标为,,
又点在反比例函数的图象上,
当,,即点坐标为,,
,
.
故答案为:3.
【点睛】本题考查的是反比例函数系数的几何意义,即在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是,且保持不变.
23. 6
【分析】(1)利用P是线段的三等分点(靠近点A),得到,根据得到,设点的横坐标为(),则,表示出,利用反比例函数的图象经过点P,即可求得,求得点的坐标;
(2)由(1)知,,求得点的坐标为,判断出直线的解析式为,由题意得,得到,最后利用的面积为,列出方程即可求解.
【详解】解:(1)∵P是线段的三等分点(靠近点A),
∴,
∵,
∴,
∵,
设点的横坐标为(),则,
∴纵坐标为,
∴,
∵反比例函数的图象经过点P,
∴,解得,
∴,
故答案为:
(2)由(1)知,,
∵,
∴点的坐标为,
则直线的解析式为,
由题意得,解得或,
∵点在第一象限,
∴,
∵的面积为,
∴,
解得,
故答案为:6
【点睛】本题考查了反比例函数的图象和性质,理解掌握反比例函数图象上点的坐标特征是解题的关键.
24.(1)
(2)
【分析】(1)将点代入解析式即可求解,
(2)根据反比例函数图象的性质求解即可.
【详解】(1)解:将点代入解析式得,
解得
(2)当时,
当时,
当时,的图象,随的增大而减小,
【点睛】本题考查了反比例函数的定义以及反比例函数图像的性质,掌握反比例函数的图象的性质是解题的关键.
25.(1)
(2)6
(3)或
【分析】(1)先利用待定系数法求得两函数的解析式,再联立方程组求解点B坐标即可;
(2)先求得直线与y轴的交点C的坐标得到,再由求解即可;
(3)根据图像直接求解即可.
【详解】(1)解:把代入,得:,解得:,
∴;
把代入,得:,解得:,
∴;
联立,解得:或,
∴.
(2)解:设与y轴交于点C,当时,,
∴,则,
∴.
(3)解:当或时,,
∴不等式的解集为或.
【点睛】本题考查反比例函数与一次函数的交点问题,涉及待定系数法函数解函数解析式、坐标与图形、解二元一次方程组、图像法解不等式的解集等知识,理解题意,利用数形结合思想求解是解答的关键.
26.(1)
(2)125字/分钟
【分析】(1)根据录入的时间录入总量录入速度即可得出函数关系式;
(2)设冉冉实际用了t分钟,则原计划用时分钟,由题意得关于t的分式方程,解方程即可求出t的值.
【详解】(1)解:设
把代入 得,
,
∴y与x的函数表达式为 ;
(2)设冉冉实际用了t分钟,则原计划用时分钟,原来的录入速度为x字/分钟
由题意得, ,
整理得: ,
∵录入速度提高了,则实际录入速度为字/分,
则 即 ,
解得:,
经检验是原方程的解,
冉冉原录入速度为:(字/分钟),
答:冉冉原来的录入速度为125字/分钟.
【点睛】本题考查了反比例函数的应用、解分式方程,根据工作量得到等量关系是解决本题的关键.
27.(1)
(2)①当时,;当时,;
②销售价格定为80元/件时,获得的利润最大,最大利润是100百元
【分析】(1)把把代入得,设y与x的函数关系式为:y=kx+b,把x=40,y=6;x=60,y=4,代入解方程组即可得到结论;
(2)①根据x的范围分类讨论,由“总利润=单件利润×销售量”可得函数解析式;
②结合①中两个函数解析式,分别依据二次函数的性质和反比例函数的性质求其最值即可.
【详解】(1)解:把代入得.
设y与x的函数关系式为:,
∵当时,,当时,,
∴,
解得:,
∴y与x的函数关系式为:.
(2)①当时,;
当时,;
②当时,,
∵随x的增大而增大.
∴当 (百元).
当时,
∵,
∴w随x的增大而增大,当时, (百元).
答:销售价格定为80元/件时,获得的利润最大,最大利润是100百元.
【点睛】本题主要考查二次函数和反比例函数的应用,理解题意依据相等关系列出函数解析式,并熟练掌握二次函数和反比例函数的性质是解题的关键.
28.(1)1<x<2
(2)4
【分析】(1)根据图象即可求得;
(2)设A(1,k2),B(2,),由S△AOB=S△AOM+S梯形AMNB﹣S△BON=S梯形AMNB得到关于k2的方程,解方程即可.
【详解】(1)直线y=k1x+b与双曲线y(x>0)交于A,B两点,且点A,B的横坐标分别是1和2,
由图象可知:不等式k1x+b的解集是1<x<2;
(2)作AM⊥x轴于M,BN⊥x轴于N,则S△AOM=S△BON|k2|,
设A(1,k2),B(2,),
∵△AOB的面积为3,
∴S△AOB=S△AOM+S梯形AMNB﹣S△BON=S梯形AMNB(k2)×(2﹣1)=3,
∴k2=4.
∴k2的值为4.
【点睛】本题是反比例函数与一次函数的交点问题,考查了反比例函数图象上点的坐标特征以及三角形面积等,数形结合是解题的关键.
29.(1)反比例函数解析式为,一次函数解析式为;(2)10.5;(3)或
【分析】(1)把的坐标代入反比例函数的解析式求出,把的坐标代入反比例函数解析式求出,把,的坐标代入一次函数的解析式得出方程组,求出方程组的解即可;
(2)求出一次函数与x轴的交点坐标,得到的值,根据三角形的面积公式求出即可;
(3)结合图象和,的坐标即可求出答案.
【详解】解:(1)∵把A(-2,-5)代入代入得:,
∴,
∴反比例函数解析式为,
∵把C(5,n)代入得反比例函数中得:,
∴C点的坐标为(5,2),
∵把A、C的坐标代入得:,
∴
∴一次函数解析式为;
(2)把y=0代入得:x=3,
∴D点坐标为(3,0),
∴OD=3,
∴;
(3)根据函数图像可知,当时,即一次函数图像在反比例函数图像的下方时自变量的取值范围,
∴当时,或.
【点睛】本题考查了反比例函数和一次函数解析式的确定、图形的面积求法及函数图象与不等式等知识点,正确求得函数解析式是解决问题的关键,解决本题注意利用数形结合思想.
30.(1),
(2)
【分析】(1)先将点A的坐标代入反比例函数的解析式,求出m的值,再把点B的坐标代入反比例函数的解析式,即可求出n的值;
(2)作轴于点C,轴于点D,根据、进行求解即可.
【详解】(1)把带入得:,
∴,
把带入得:;
(2)作轴于点C,轴于点D,
则,
∵,
∴.
【点睛】本题考查了待定系数法求反比例函数的解析式,求反比例函数图象上点的坐标,比例系数k的几何意义,反比例函数与图形的面积,熟练掌握知识点是解题的关键.
31.(1)
(2)区域内的格点坐标有3个,分别为,,.
【分析】(1)将点代入反比例函数即可求解;
(2)当直线经过格点,点,求出直线的解析式,结合图象即可求得内的格点坐标及个数;
【详解】(1)将点代入反比例函数,得:
,
∴,
∴反比例函数的表达式为:;
(2)∵直线经过格点,点,
∴,
解得:,
∴直线的解析式为,
如图所示:
∵点,轴于点,
∴点,
故区域的左边界为线段的部分,其解析式为:,
上方的边界为线段的部分,其解析式为,
令,得:,
∴点坐标为:,
故当时,,即与,
当时,,即,
∴区域内的格点坐标有3个,分别为,,.
【点睛】本题考查一次函数与反比例函数的图象及性质,熟练掌握待定系数法求解析式是解题的关键是,学会利用数形结合的思想.
